i denna handledning kommer vi att lära oss om Wheatstone Bridge. Vi kommer att se arbetsprincipen för Wheatstone Bridge, få exempelkretsar och några viktiga applikationer.

introduktion till Wheatstone Bridge

i den verkliga världen stöter vi på olika signaler, några av dem mäts av förändringar i motstånd och några av dem är med induktans och kapacitans.

om vi betraktar motståndet, de flesta industriella sensorer som temperatur, belastning, fuktighet, förskjutning, vätskenivå etc. producerar värdeförändringen av motståndet för en variabel förändring. Därför finns det ett behov av en signalkonditionering för varje motståndssensor.

generellt är resistansmätningen uppdelad i tre typer, mätning av låg resistans, mätning av medelmotstånd och mätning av hög resistans. Om motståndsmätningen möjligen är från några milliohm till mikro ohm, betraktas den som en mätning med låg resistans.

denna mätning används faktiskt för forskningsändamål. Om mätningen är från 1 ohm till 100 k kallas vanligtvis en mätning av medelmotstånd. Potentiometer, termistorer etc. mätning kommer under denna kategori.

och mycket hög resistansmätning anses från 100 kilo ohm till större än 100 mega ohm. För att hitta medelvärdet av motståndet används olika metoder, men mestadels Wheatstone bridge används.

Vad är Wheatstone Bridge?

det vanligaste och enklaste bronätet för att hitta motståndet är DC Wheatstone Bridge. Denna bro används där små förändringar i motstånd ska mätas som i sensorapplikationer. Detta används för att omvandla en motståndsändring till en spänningsändring av en givare.

kombinationen av denna bro med operationsförstärkare används i stor utsträckning i industrier för olika givare och sensorer. En Wheatstone bridge består av fyra motstånd som är anslutna i form av en diamant med matningskällan och indikerar instrument som visas i figur.

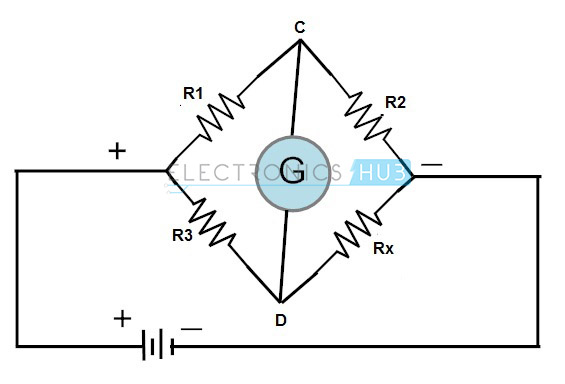
denna bro används för att hitta det okända motståndet mycket exakt genom att jämföra det med ett känt värde av motstånd. I denna bro används null eller balanserat tillstånd för att hitta motståndet.

för denna bro balanserad skick spänning vid punkterna C och D måste vara lika. Därför strömmar ingen ström genom galvanometern. För att få det balanserade tillståndet måste ett av motstånden vara variabelt.

From the figure,

The voltage at point D = V × RX / (R3 + RX)

The voltage at point C = V × R2 / (R1 + R2)

The voltage (V) across galvanometer or between C and D is,

VCD = V × RX / (R3 + RX) − V R2 / (R1 + R2)

When the bridge is balanced VCD = 0,

So,

V × RX / (R3 + RX) = V R2 / (R1 + R2)

RXR1 + RXR2 = R2R3 + R2RX

R1RX= R2R3

R2/R1= RX/R3

This är villkoret att balansera bron. Och för att hitta det okända värdet av resistans

RX = R3 (R2 / R1)

från ovanstående ekvation R4 eller Rx kan beräknas från det kända värdet av resistans R3 och förhållandet R2/R1. Därför är de flesta fallen R2-och R1-värden fasta och R3-värdet är variabelt så att null-värdet uppnås och bron balanseras.

arbetsprincip

utan galvanometern ser brokretsen bara ut som en spänningsdelarkrets som visas i figuren nedan. Tänk på R1= 20 ohm, R2= 40 ohm för en arm och för den andra överväga samma värden på R3 respektive R4.

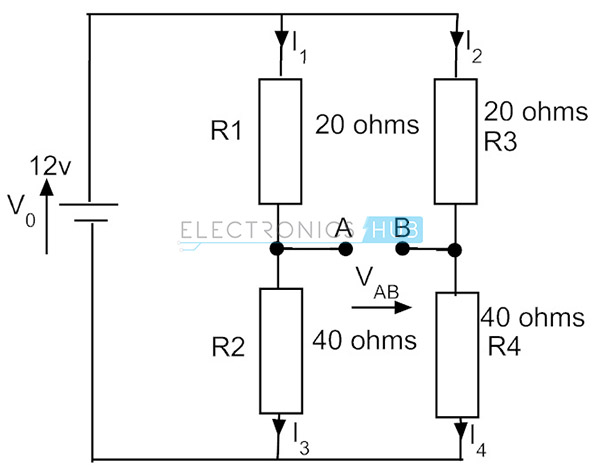
nuvarande flöde i första armen är

I1 = V/ (R1+R2)

I1 = 12V/ (20+40)

I1 = 0,2 A

och spänning vid punkt C är lika med spänningsfallet vid motståndet R2,

VR2 = I1 cu R2= 0,2 40 = 8v

på samma sätt är spänningen över r1 4V (0,2 20 ci). På grund av samma motståndsvärden kommer spänningarna vid R4 och R3 att vara desamma som för R1 respektive R2. Därför är spänningarna vid punkterna A och B desamma, därför visar galvanometern nollavläsning eftersom potentialskillnaden är noll. I detta fall sägs bron vara i balanserat skick.

Antag att om vi vänder motstånden i den andra armen är strömflödet detsamma på grund av seriekretsen. Men spänningen över motståndet R4 ändras, dvs 0,2 * 20 = 4V. Så vid detta tillstånd spänning över punkterna A och B är olika och existerar en potentiell skillnad på 8 – 4 = 4V. Detta är broens obalanserade tillstånd.

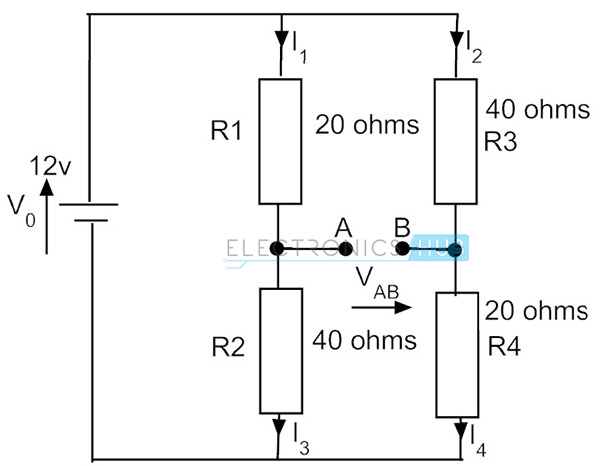
exempel på Wheatstone Bridge

från ovan är Wheatstone bridge obalanserad när voltmeteravläsningen inte är noll. Denna avläsning kan vara positiv eller negativ beror på spänningarnas storlek vid mätterminalerna. Låt oss överväga den nedan kretsen av Wheatstone bridge som är ansluten för att hitta det okända motståndsvärdet med användning av resistor decade box för att få det variabla motståndet hos R3.

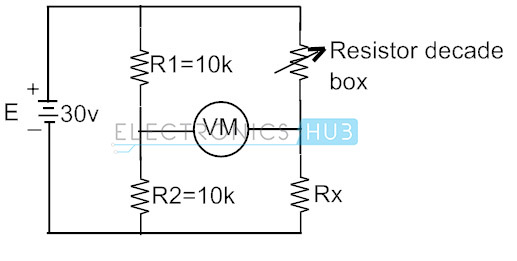
vi vet att villkoret för bridge balance är

R4 = R3 kg R2 / R1

Rx = RBOX 103)/ (10 x 103)

RX = RBOX

här i detta fall balanseras Wheatstone Bridge genom att justera decenniets motståndslåda tills voltmätaren läser nollvärde. Och motsvarande motståndsvärde i lådan är lika med det okända motståndet. Antag att om spänningsnollförhållandet inträffar vid 250 ohm i resistance decade box, är det okända motståndet också 250 ohm.

Wheatstone Bridge för Töjningsmätning

oftast för mätning av töjningen används töjningsgages vars elektriska motstånd varierar med proportionerlig belastning i anordningen. I praktiken är intervallet av töjningsmätarens motstånd från 30 ohm till 3000 ohm. För en given stam kan motståndsförändringen endast vara en bråkdel av hela intervallet. Därför används Wheatstone bridge-konfiguration för att mäta extremt en bråkdel av motståndsförändringar med hög noggrannhet. Nedanstående figur visar Wheatstone bridge där det okända motståndet ersätts med en belastningsmätare.

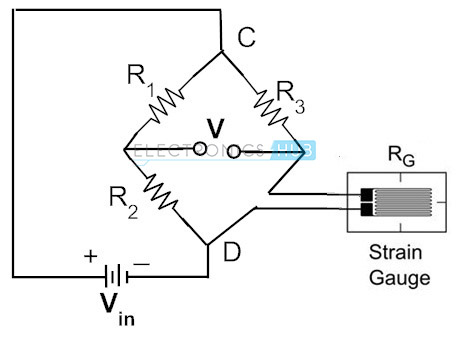
i ovanstående krets är två motstånd R1 och R2 lika med varandra och R3 är det variabla motståndet. Med ingen kraft applicerad på töjningsmätaren varieras reostat och placeras slutligen så att voltmätaren indikerar nollböjning. Detta kallas ett brobalanseringsförhållande. Detta villkor representerar att det inte finns någon belastning på mätaren.

om töjningsmätaren antingen är spänd eller komprimerad kan motståndet öka eller minska. Därför orsakar detta obalans av bron. Detta ger en spänningsindikering på voltmeter motsvarar spänningsförändringen. Om belastningen som appliceras på en belastningsmätare är mer, är spänningsskillnaden över mätterminalerna mer. Om stammen är noll, visar brobalanserna och mätaren nollavläsning.

det här handlar om motståndsmätningen med hjälp av en Wheatstone-bro för exakt mätning. På grund av fraktionsmätningen av motstånd används Wheatstone-broar mestadels i töjningsmätare och termometermätningar.

applikationer

1. Wheatstone bridge används för att mäta de mycket låga motståndsvärdena exakt.
2. Wheatstone bridge tillsammans med operationsförstärkare används för att mäta de fysiska parametrarna som temperatur, belastning, ljus etc.
3. Vi kan också mäta kvantiteterna kapacitans, induktans och impedans med hjälp av variationerna på Wheatstone bridge.