Regression till medelvärdet är ett vanligt statistiskt fenomen som kan vilseleda oss när vi observerar världen. Att lära sig känna igen när regression till medelvärdet är på spel kan hjälpa oss att undvika att misstolka data och se mönster som inte finns.

***

det är viktigt att minimera fall av dåligt omdöme och ta itu med de svaga punkterna i vårt resonemang. Att lära sig om regression till medelvärdet kan hjälpa oss.

Nobelprisvinnande psykolog Daniel Kahneman skrev en bok om fördomar som fördunklar vårt resonemang och snedvrider vår uppfattning om verkligheten. Det visar sig att det finns en hel uppsättning logiska fel som vi begår eftersom vår intuition och hjärnor inte hanterar enkel statistik. Ett av de fel som han undersöker när han tänker snabbt och långsamt är den ökända regressionen mot medelvärdet.

begreppet regression till medelvärdet utarbetades först av Sir Francis Galton. Regeln går att i alla serier med komplexa fenomen som är beroende av många variabler, där chans är inblandad, tenderar extrema resultat att följas av mer måttliga.

I söker visdom, Peter Bevelin erbjuder exempel på John, som var missnöjd med resultatet av nya medarbetare så han satte dem i en kompetenshöjande program där han mätte de anställdas skicklighet:

deras poäng är nu högre än de var på det första testet. Johns slutsats: ”det färdighetshöjande programmet orsakade förbättringen av skickligheten.”Detta är inte nödvändigtvis sant. Deras högre poäng kan vara resultatet av regression till medelvärdet. Eftersom dessa individer mättes som på den låga änden av kompetensskalan, skulle de ha visat en förbättring även om de inte hade tagit det kompetenshöjande programmet. Och det kan finnas många orsaker till deras tidigare prestanda — stress, trötthet, sjukdom, distraktion etc. Deras verkliga förmåga har kanske inte förändrats.

vår prestanda varierar alltid runt en genomsnittlig sann prestanda. Extrem prestanda tenderar att bli mindre extrem nästa gång. Varför? Testmätningar kan aldrig vara exakta. Alla mätningar består av en sann del och en slumpmässig feldel. När mätningarna är extrema kommer de sannolikt delvis att orsakas av en slump. Chansen kommer sannolikt att bidra mindre på andra gången vi mäter prestanda.

om vi byter från ett sätt att göra något till ett annat bara för att vi inte lyckas, är det mycket troligt att vi gör det bättre nästa gång även om det nya sättet att göra något är lika eller sämre.

detta är en av anledningarna till att det är farligt att extrapolera från små provstorlekar, eftersom data kanske inte är representativa för distributionen. Det är också varför James March hävdar att ju längre någon stannar i sitt jobb, ”desto mindre är den troliga skillnaden mellan den observerade prestationsrekordet och den faktiska förmågan.”Allt kan hända på kort sikt, särskilt i alla ansträngningar som innebär en kombination av skicklighet och tur. (Förhållandet mellan skicklighet och tur påverkar också regression till medelvärdet.)

Regression till medelvärdet

effekterna av regression till medelvärdet kan ofta observeras i sport, där effekten orsakar massor av omotiverade spekulationer.

Kahneman tänker snabbt och långsamt och påminner om att titta på herrhopp, en disciplin där slutresultatet är en kombination av två separata hopp. Medveten om regressionen till medelvärdet blev Kahneman förvånad över att höra kommentatorns förutsägelser om det andra hoppet. Han skriver:

Norge hade ett bra första hopp; han kommer att vara spänd, hoppas kunna skydda sin ledning och kommer förmodligen att göra värre” eller ”Sverige hade ett dåligt första hopp och nu vet han att han inte har något att förlora och kommer att vara avslappnad, vilket borde hjälpa honom att göra bättre.

Kahneman påpekar att kommentatorn hade märkt regressionen till medelvärdet och kommit fram till en historia för vilken det inte fanns några kausala bevis (se narrativ felaktighet). Detta är inte att säga att hans historia inte kunde vara sant. Kanske, om vi mätte hjärtfrekvensen före varje hopp, skulle vi se att de är mer avslappnade om det första hoppet var dåligt. Men det är inte poängen. Poängen är att regression till medelvärdet händer när lycka spelar en roll, som det gjorde i resultatet av det första hoppet.

lektionen från sport gäller alla aktiviteter där chans spelar en roll. Vi bifogar ofta förklaringar om vårt inflytande över en viss process till framstegen eller bristen på den.

i verkligheten är vetenskapen om prestanda komplex, situationsberoende och ofta är mycket av det vi tycker är inom vår kontroll verkligen slumpmässigt.

När det gäller skidhopp kommer en stark vind mot bygeln att leda till att även den bästa idrottaren visar mediokra resultat. På samma sätt kan en stark vind-och skidförhållanden till förmån för en medioker hoppare leda till en betydande, men en tillfällig bump i hans resultat. Dessa effekter kommer dock att försvinna när förhållandena ändras och resultaten kommer att återgå till det normala.

detta kan få allvarliga konsekvenser för coaching och prestationsspårning. Regressionsreglerna föreslår att vi vid utvärdering av prestanda eller anställning måste förlita oss på track records mer än resultat av specifika situationer. Annars är vi benägna att bli besvikna.

När Kahneman höll en föreläsning till israeliska flygvapnet om psykologin för effektiv träning, delade en av officerarna sin erfarenhet att utvidga beröm till sina underordnade ledde till sämre prestanda, medan skällning ledde till en förbättring av efterföljande ansträngningar. Som en konsekvens, han hade vuxit till att vara generös med negativ feedback och hade blivit ganska försiktig med att ge för mycket beröm.

Kahneman upptäckte omedelbart att det var regression till medelvärdet på jobbet. Han illustrerade missuppfattningen genom en enkel övning kanske du vill prova själv. Han ritade en cirkel på en tavla och bad sedan officerarna en efter en att kasta en bit krita i mitten av cirkeln med ryggen mot tavlan. Han upprepade sedan experimentet och registrerade varje officers prestation i den första och andra rättegången.

naturligtvis tenderade de som gjorde otroligt bra på första försöket att göra värre på sitt andra försök och vice versa. Felaktigheten blev omedelbart klar: förändringen i prestanda sker naturligt. Det är återigen inte att säga att feedback inte spelar någon roll alls – kanske det gör det, men tjänstemannen hade inga bevis för att dra slutsatsen att det gjorde det.

den ofullkomliga korrelationen och chansen

Vid denna tidpunkt kanske du undrar varför regressionen till medelvärdet händer och hur vi kan se till att vi är medvetna om det när det inträffar.

för att förstå regression till medelvärdet måste vi först förstå korrelation.

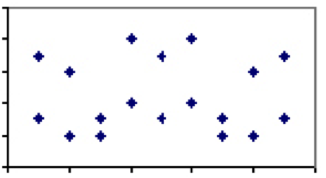
korrelationskoefficienten mellan två mått som varierar mellan -1 och 1 är ett mått på den relativa vikten av de faktorer de delar. Till exempel, två fenomen med få faktorer delade, såsom flaskvattenförbrukning kontra självmordsfrekvens, bör ha en korrelationskoefficient på nära 0. Det vill säga, om vi tittade på alla länder i världen och planerade självmordsnivåer för ett visst år mot konsumtion av flaskvatten per capita, skulle tomten inte visa något mönster alls.

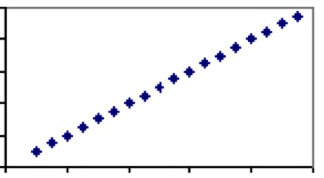
tvärtom finns det åtgärder som enbart är beroende av samma faktor. Ett bra exempel på detta är temperaturen. Den enda faktor som bestämmer temperaturen – molekylernas hastighet-delas av alla skalor, varför varje grad i Celsius kommer att ha exakt ett motsvarande värde i Fahrenheit. Därför temperaturen i Celsius och Fahrenheit kommer att ha en korrelationskoefficient på 1 och tomten kommer att vara en rak linje.

det finns få om några fenomen i humanvetenskap som har en korrelationskoefficient på 1. Det finns dock mycket där föreningen är svag till måttlig och det finns en viss förklarande kraft mellan de två fenomenen. Tänk på sambandet mellan höjd och vikt, vilket skulle landa någonstans mellan 0 och 1. Medan nästan varje treåring blir lättare och kortare än varje vuxen man, kommer inte alla vuxna män eller treåringar av samma höjd att väga samma.

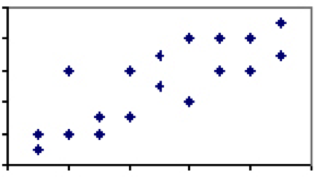
denna variation och motsvarande lägre grad av korrelation innebär att, medan höjden generellt sett är en bra prediktor, finns det tydligt andra faktorer än höjden på spel. När korrelationen mellan två åtgärder är mindre än perfekt måste vi se upp för effekterna av regression till medelvärdet.

Kahneman observerade en allmän regel: när korrelationen mellan två poäng är ofullkomlig kommer det att regression till medelvärdet.

detta kan först verka förvirrande och inte särskilt intuitivt, men graden av regression till medelvärdet är direkt relaterad till graden av korrelation mellan variablerna. Denna effekt kan illustreras med ett enkelt exempel.

anta att du är på en fest och fråga varför det är att mycket intelligenta kvinnor tenderar att gifta sig med män som är mindre intelligenta än de är. De flesta människor, även de med viss utbildning i statistik, kommer snabbt att hoppa in med en mängd kausala förklaringar som sträcker sig från undvikande av konkurrens till rädslan för ensamhet som dessa kvinnor möter. Ett ämne av sådan kontrovers kommer sannolikt att väcka en stor debatt.

nu, vad händer om vi frågade varför korrelationen mellan makarnas intelligenspoäng är mindre än perfekt? Denna fråga är knappast lika intressant och det finns lite att gissa – vi vet alla att detta är sant. Paradoxen ligger i det faktum att de två frågorna råkar vara algebraiskt likvärdiga. Kahneman förklarar:

om korrelationen mellan makarnas intelligens är mindre än perfekt (och om män och kvinnor i genomsnitt inte skiljer sig åt i intelligens) är det en matematisk oundviklighet att mycket intelligenta kvinnor kommer att gifta sig med män som i genomsnitt är mindre intelligenta än de är (och vice versa, förstås). Den observerade regressionen till medelvärdet kan inte vara mer intressant eller mer förklarbar än den ofullkomliga korrelationen.

förutsatt att korrelationen är ofullkomlig är chansen att två partners representerar topp 1% i termer av någon egenskap mycket mindre än en partner som representerar topp 1% och den andra – botten 99%.

orsaken, effekten och behandlingen

Vi bör vara särskilt försiktiga med regressionen till medelfenomenet när vi försöker fastställa orsakssamband mellan två faktorer. När korrelationen är ofullkomlig kommer det bästa alltid att bli värre och det värsta verkar bli bättre med tiden, oavsett ytterligare behandling. Detta är något som de allmänna medierna och ibland till och med utbildade forskare inte känner igen.

Tänk på exemplet Kahneman ger:

deprimerade barn som behandlas med en energidryck förbättras avsevärt under en tremånadersperiod. Jag gjorde upp denna tidningsrubrik, men det faktum att det rapporterar är sant: om du behandlade en grupp deprimerade barn under en tid med en energidryck, skulle de visa en kliniskt signifikant förbättring. Det är också så att deprimerade barn som spenderar lite tid på att stå på huvudet eller krama en katt i tjugo minuter om dagen också kommer att visa förbättringar.

När man stöter på sådana rubriker är det väldigt frestande att hoppa till slutsatsen att energidrycker, stående på huvudet eller kramar katter är alla perfekt livskraftiga botemedel mot depression. Dessa fall förkroppsligar emellertid återigen regressionen till medelvärdet:

deprimerade barn är en extrem grupp, de är mer deprimerade än de flesta andra barn—och extrema grupper återgår till medelvärdet över tiden. Korrelationen mellan depressionspoäng vid på varandra följande tillfällen av testning är mindre än perfekt, så det kommer att regression till medelvärdet: deprimerade barn kommer att bli något bättre med tiden även om de kramar inga katter och dricker ingen Red Bull.

Vi tillskriver ofta felaktigt en specifik policy eller behandling som orsak till en effekt, när förändringen i de extrema grupperna skulle ha hänt ändå. Detta utgör ett grundläggande problem: hur kan vi veta om effekterna är verkliga eller helt enkelt på grund av variation?

lyckligtvis finns det ett sätt att berätta mellan en verklig förbättring och regression till medelvärdet. Det är introduktionen av den så kallade kontrollgruppen, som förväntas förbättras genom regression ensam. Syftet med forskningen är att avgöra om den behandlade gruppen förbättrar mer än regression kan förklara.

i verkliga situationer med prestanda för specifika individer eller lag, där det enda verkliga riktmärket är tidigare prestanda och ingen kontrollgrupp kan introduceras, kan effekterna av regression vara svåra om inte omöjliga att disentangle. Vi kan jämföra med branschgenomsnittet, kamrater i kohortgruppen eller historiska förbättringshastigheter, men ingen av dessa är perfekta åtgärder.

***

lyckligtvis medvetenhet om regressionen till medelfenomenet i sig är redan ett bra första steg mot en mer noggrann inställning till förståelse av tur och prestanda.

om det finns något att lära sig från regressionen till medelvärdet är det vikten av track records snarare än att förlita sig på engångs framgångshistorier. Jag hoppas att nästa gång du stöter på en extrem kvalitet som delvis styrs av en slump kommer du att inse att effekterna sannolikt kommer att regressera över tiden och kommer att anpassa dina förväntningar i enlighet därmed.

vad du ska läsa nästa

• uppgradera ditt tänkande med 113 mentala modeller förklarade.
• läs om tänkande på andra nivån så att du kan undvika negativa konsekvenser.