Redaktörens anteckning

följande studentforskningsrapport utarbetades för Professor Judit Kardos Math 255-klass, som hölls vid College of New Jersey. Detta var en 3-kredit introduktionskurs i matematikens historia. Denna rapport räknades till 30% av slutbetyget. Det är ett exempel på den typ av historiska forskarstuderande kan göra med hjälp av sekundära källor.

Leonard Eulers lösning på K: S problem med bron i K: N.

k: n.

vår historia börjar på 18th century, i den pittoreska staden K: N. År 1254 grundade Teutonic knights staden K Kubnigsberg under ledning av den bohemiska kungen Ottoker II efter deras andra korståg mot preussarna. Under medeltiden blev k Jacobnigsberg en mycket viktig stad och handelscentrum med sitt läge strategiskt beläget vid floden. Konstverk från sjuttonhundratalet visar K Xianigsberg som en blomstrande stad, där flottor av fartyg fyller Pregel, och deras handel erbjuder en bekväm livsstil för både de lokala köpmännen och deras familjer. Den hälsosamma ekonomin gjorde det möjligt för stadens folk att bygga sju broar över floden, varav de flesta kopplade till Ön Kneiphof; deras platser kan ses på den medföljande bilden .

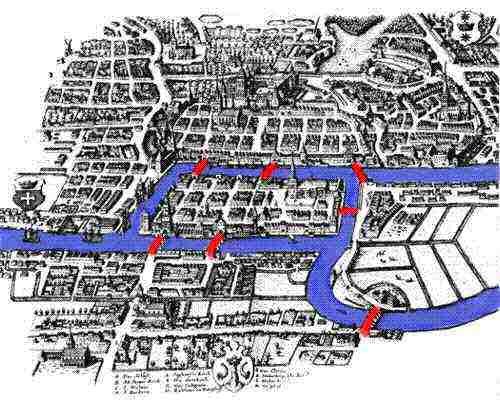
När floden flödade runt Kneiphof, som bokstavligen betyder pubgård och en annan ö, delade den staden i fyra olika regioner. De sju broarna kallades Blacksmith ’s bridge, Anslutande bro, grön bro, Merchant’ s Bridge, träbro, High Bridge och Honey Bridge. Enligt lore brukade medborgarna i K Jacobnigsberg tillbringa söndagseftermiddagar som gick runt sin vackra stad. När de gick bestämde sig stadens folk för att skapa ett spel för sig själva, deras mål var att utforma ett sätt på vilket de kunde gå runt i staden och korsa var och en av de sju broarna bara en gång. Även om ingen av medborgarna i K Kubnigsberg kunde uppfinna en rutt som skulle göra det möjligt för dem att korsa var och en av broarna bara en gång, kunde de fortfarande inte bevisa att det var omöjligt. Tur för dem, k Jacobnigsberg var inte för långt från St Petersburg, hem för den berömda matematikern Leonard Euler.

Euler och Broproblemet

varför skulle Euler bekymra sig om ett problem som inte är relaterat till matematikområdet? Varför skulle en sådan stor matematiker tillbringa en hel del tid med ett trivialt problem som k Jacobnigsberg Bridge Problem? Euler var uppenbarligen en upptagen man och publicerade mer än 500 böcker och papper under sin livstid. Bara 1775 skrev han i genomsnitt ett matematiskt papper per vecka, och under sin livstid skrev han om olika ämnen förutom matematik inklusive mekanik, optik, astronomi, navigering och hydrodynamik. Det är inte förvånande att Euler ansåg att detta problem var trivialt och uppgav i ett brev från 1736 till Carl Leonhard Gottlieb Ehler, borgmästare i Danzig, som bad honom om en lösning på problemet :

. . . Således ser du, mest ädla Herre, hur denna typ av lösning har liten relation till matematik, och jag förstår inte varför du förväntar dig att en matematiker ska producera den, snarare än någon annan, för lösningen är baserad på förnuft ensam, och dess upptäckt beror inte på någon matematisk princip. På grund av detta vet jag inte varför även frågor som har så lite relation till matematik löses snabbare av matematiker än av andra.

Även om Euler fann problemet trivialt, var han fortfarande fascinerad av det. I ett brev skrivet samma år till Giovanni Marinoni, en italiensk matematiker och ingenjör, sa Euler,

denna fråga är så banal, men tycktes mig värd uppmärksamhet i den geometrin, inte heller algebra, inte ens konsten att räkna var tillräcklig för att lösa det.

Euler trodde att detta problem var relaterat till ett ämne som Gottfried Wilhelm Leibniz en gång hade diskuterat och längtat efter att arbeta med, något Leibniz kallade geometria situs, eller geometri av position. Denna så kallade positionsgeometri är det som nu kallas grafteori, som Euler introducerar och använder när han löser detta kända problem.

Eulers bevis

den 26 augusti 1735 presenterar Euler ett papper som innehåller lösningen på Konigsbergs broproblem. Han tar upp både detta specifika problem, liksom en allmän lösning med valfritt antal landmassor och valfritt antal broar. Denna uppsats, kallad ’Solutio problematis ad geometriam situs pertinentis’, publicerades senare 1741 . Eulers papper är uppdelat i tjugo numrerade stycken, och i det följande kommer en förenklad version av Eulers stycken att presenteras.

i de två första styckena i Eulers bevis introducerar han Konigsberg Bridge-problemet. I punkt 1 säger Euler att han anser att detta problem gäller geometri, men inte den geometri som är välkänd av hans samtida, som involverar mätningar och beräkningar, utan istället en ny typ av geometri, som Leibniz kallade geometri av Position. Sedan i punkt 2 förklarar Euler för sin publik hur Konigsberg-problemet fungerar. Euler tillhandahöll en skiss av problemet (se Eulers Figur 1) och kallade de sju distinkta broarna: a, b, c, D, e, f och g. i denna paragraf anger han den allmänna frågan om problemet, ”kan man ta reda på om det är möjligt att korsa varje bro exakt en gång?”

Eulers Figur 1 från ”Solutio problematis ad geometriam situs pertinentis”, Enestr ug 53

efter att ha angett den allmänna frågan han försöker lösa börjar Euler utforska olika metoder för att hitta en lösning. I punkt 3 berättar Euler läsaren att för att lösa detta specifika problem kunde han skriva ner alla möjliga vägar, men denna teknik skulle ta mycket tid och skulle inte fungera för större konfigurationer med fler broar och landmassor. På grund av dessa problem beslutade Euler att välja en annan metod för att lösa detta problem.

i punkt 4 börjar han förenkla problemet genom att uppfinna ett bekvämt system för att representera korsningen av en bro. Euler beslutar att istället för att använda små bokstäver för att representera korsningen av en bro skulle han skriva de stora bokstäverna som representerar landmassorna. Till exempel, hänvisar hans figur 1, AB skulle innebära en resa som startade i landmass a, och slutade i B. Dessutom, om efter att ha rest från landmass A till B, någon bestämmer sig för att flytta till landmass D, detta skulle helt enkelt betecknas, ABD. I punkt 5 fortsätter Euler sin diskussion om denna process och förklarar att i ABDC, även om det finns fyra stora bokstäver, korsades bara tre broar. Euler förklarar att oavsett hur många broar det finns, kommer det att finnas ytterligare ett brev för att representera den nödvändiga korsningen. På grund av detta krävde hela K-Kubnigsberg-Broproblemet att sju broar skulle korsas, och därför åtta stora bokstäver.

i punkt 6 fortsätter Euler att förklara detaljerna i sin metod. Han berättar för läsaren att om det finns mer än en bro som kan korsas när man går från en landmassa till den andra, spelar det ingen roll vilken bro som används. Till exempel, även om det finns två broar, a och b, som kan ta en resenär från A till B, spelar det ingen roll med Eulers notation vilken bro som tas. I denna paragraf diskuterar Euler också det specifika problemet han har att göra med. Han förklarar, med hjälp av sin ursprungliga figur, att k Kubnigsberg-problemet behöver exakt åtta bokstäver, där paren (A,B) och (A,C) måste visas bredvid varandra exakt två gånger, oavsett vilken bokstav som visas först. Dessutom måste paren (A,D), (B,D) och (C, D) inträffa tillsammans exakt en gång för att en väg som korsar varje bro en gång och bara en gång ska existera.

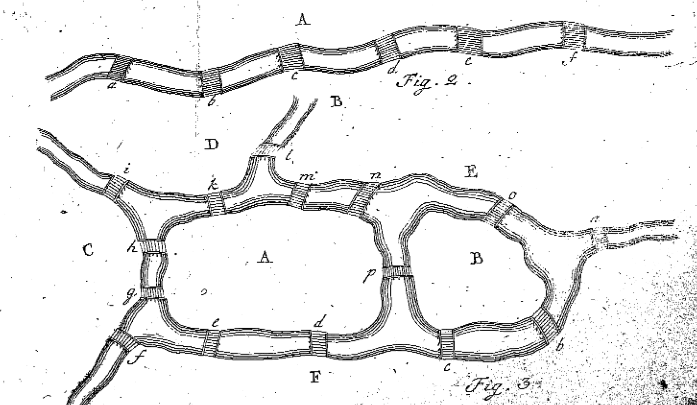
Eulers siffror 2 och 3 från ’Solutio problematis ad geometriam situs pertinentis,’ Enestr Uigm 53

i punkt 7 informerar Euler läsaren om att han antingen behöver hitta en sekvens med åtta bokstäver som uppfyller problemet, eller att han måste bevisa att ingen sådan sekvens existerar. Innan han gör detta för K Kubnigsberg Bridge-problemet bestämmer han sig för att hitta en regel för att upptäcka om det finns en väg för ett mer allmänt problem. Han gör detta i punkt 8 genom att titta på mycket enklare exempel på landmassor och broar. Euler drar Figur 2, och han börjar bedöma de situationer där region a färdas igenom. Euler säger att om bro a Reste en gång var a antingen där resan började eller slutade och användes därför bara en gång. Om broar a, b och c alla Reste en gång används a exakt två gånger, oavsett om det är start-eller slutplatsen. På samma sätt, om fem broar leder till A, skulle landmassan a inträffa exakt tre gånger på resan. Euler säger att ” i allmänhet, om antalet broar är något udda tal, och om det ökas med en, är antalet förekomster av A hälften av resultatet.”Med andra ord, om det finns ett udda antal broar som förbinder A till andra landmassor, Lägg till en till antalet broar och dela den med två för att ta reda på hur många totala gånger A måste användas i banan, där varje bro används en gång och bara en gång (dvs. Totala förekomster av A där A har en udda # broar = (#broar – 1) / 2 ).

med hjälp av detta faktum löser Euler K-problemet i punkt 9. I så fall, eftersom det finns fem broar som leder till en, Det måste ske tre gånger (se hans figur 1, ovan). På samma sätt måste B, C och D visas två gånger eftersom de alla har tre broar som leder till dem. Därför 3(För a) + 2(för B) + 2(för C) + 2(för D) = 9, Men Euler uppgav redan att det bara får finnas åtta händelser för de sju broarna. Detta är en motsägelse! Därför är det omöjligt att resa broarna i staden K Jacobnigsberg en gång och bara en gång. Slutet, eller är det? Medan folket i K Kubnigsberg kan vara nöjda med den här lösningen var den stora matematikern Leonhard Euler inte nöjd. Euler fortsätter vidare sitt bevis för att hantera mer allmänna situationer.

Eulers generalisering

i punkt 10 fortsätter Euler sin diskussion genom att notera att om situationen involverar alla landmassor med ett udda antal broar, är det möjligt att berätta om en resa endast kan göras med varje bro en gång. Euler säger att om summan av antalet gånger varje bokstav måste visas är en mer än det totala antalet broar, kan en resa göras. Men om antalet händelser är större än en mer än antalet broar, kan en resa inte göras, som k Jacobnigsberg Bridge-problemet. Detta beror på att regeln, som Euler ger för ett udda antal broar, med hjälp av hans figur 2, gäller för den allmänna situationen om det bara finns en annan landmassa eller mer än en.

i punkterna 11 och 12 behandlar Euler situationen där en region har ett jämnt antal broar kopplade till den. Denna situation visas inte i K-Kubnigsberg-problemet och har därför ignorerats hittills. I situationen med en landmass X med ett jämnt antal broar kan två fall uppstå. Det första fallet är när X är utgångspunkten för resan. I det här fallet visas X två gånger, en gång som startpunkt och igen som slutpunkt. I det andra fallet är X inte utgångspunkten. Om detta skulle hända skulle X bara visas en gång, eftersom resan måste gå in genom en bro och omedelbart lämna genom den enda andra tillgängliga. På samma sätt, om det finns fyra broar kopplade till X beror antalet förekomster av X på om det är en utgångspunkt eller inte. Om resan börjar i X måste den visas tre gånger, men om den inte börjar i X visas den bara två gånger. Så i allmänhet, om X har ett jämnt antal broar kopplade, så om resan inte startar i X, visas X hälften av antalet gånger som broar (dvs. Förekomster av X där X är jämn och inte utgångspunkten = (# Of Bridges) / 2). Om resan startar i X visas X halva antalet gånger som broar, plus en (dvs. förekomster av X där X är jämn och startpunkt = ((#Of Bridges) / 2) + 1).

i punkterna 13 till 15 förklarar Euler hur man kan ta reda på om en väg som använder varje bro en gång och bara en gång finns och presenterar sitt eget exempel för att visa hur det fungerar. Euler förklarar först sin enkla sexstegsmetod för att lösa alla allmänna situationer med landmassor dividerade med floder och förbundna med broar. Första Euler betecknar varje landmassa med en bokstav. För det andra tar han det totala antalet broar, lägger till en, och skriver detta ovanför diagrammet han håller på att göra. Därefter tar han stora bokstäver, lägger dem i en kolumn och bredvid dem skriver antalet broar. För det fjärde anger han med asterisker landmassorna som har ett jämnt antal broar. Sedan, bredvid varje jämnt nummer, skriver han megapixel av numret och bredvid varje udda nummer placerar han siffran plus ett. Slutligen lägger Euler till siffrorna skrivna i kolumnen till höger och om summan är en mindre än eller lika med antalet broar plus en, är den nödvändiga resan möjlig. Det är dock viktigt att notera att om summan är en mindre än antalet broar plus en, måste resan börja från en av landmassorna markerade med en asterisk. Om summan är lika med antalet broar plus en måste resan börja i en region som inte är markerad med en asterisk.

exempel

använda Konigsberg problemet som hans första exempel Euler visar följande:

antal broar = 7, antal broar plus en = 8

Region broar gånger Region måste visas

a 5 3

b 3 2

C 3 2

D 3 2

men, 3 + 2 + 2 + 2 = 9, vilket är mer än 8, så resan är omöjlig.eftersom detta exempel är ganska grundläggande beslutar Euler att utforma sin egen situation med två öar, fyra floder och femton broar. Situationen Euler skapade kan ses i hans figur 3, ovan. Euler försöker nu ta reda på om det finns en väg som tillåter någon att gå över varje bro en gång och bara en gång. Euler följer samma steg som ovan, namnger de fem olika regionerna med stora bokstäver och skapar en tabell för att kontrollera det om det är möjligt, som följande:

antal broar = 15, antal broar plus en = 16

Region broar gånger Region måste visas

b* 8 4

b* 4 2

C* 4 2

D 3 2

e 5 3

F* 6 3

dessutom, 4 + 2 + 2 + 2 + 3 + 3 = 16, vilket motsvarar antalet broar, plus en, vilket innebär att resan faktiskt är möjlig. Eftersom summan är lika med antalet broar plus en, måste resan börja i antingen D eller E. Nu när Euler vet att det är möjligt att göra en resa, allt han behöver göra är att ange vad vägen kommer att bli. Euler väljer vägen EaFbBcFdAeFfCgAhCiDkAmEnApBoElD, där han inkluderar vilka broar som korsas mellan bokstäverna som representerar landmassorna. Även om denna information är främmande, eftersom den exakta bron inte spelar någon roll för att veta att en resa är möjlig, är den användbar när du väljer en väg. Detta är ett bra exempel som visar den metod som Euler skulle använda när man löser något problem av detta slag.

Eulers slutsatser

i de närmaste styckena presenterar Euler ett annat sätt att ta reda på om en resa kan göras med tanke på någon uppsättning landmassor, broar och floder. I punkt 16 påpekar Euler att summan av de nummer som anges direkt till höger om landmassorna uppgår till dubbelt så många broar. Detta faktum blir senare känt som handskakande lemma. I grund och botten säger handskakningen lemma att varje bro räknas två gånger, en gång för varje landmassa som den är fäst vid. I punkt 17 anger Euler att summan av alla broar som leder till varje region är jämn, eftersom hälften av detta antal är lika med det totala antalet broar. Detta är dock omöjligt om det finns ett udda antal landmassor med ett udda antal broar. Därför bevisar Euler att om det finns några udda nummer kopplade till landmassor måste det finnas ett jämnt antal av dessa landmassor.

detta är dock inte tillräckligt för att bevisa när det finns en väg där varje bro används en gång och bara en gång, eftersom K. På grund av detta lägger Euler till fler begränsningar i punkterna 18 och 19. Euler förklarar att eftersom summan av antalet broar som är fästa vid varje landmassa är lika med dubbelt så många broar (som ses i handskakningen lemma), så därför om du lägger till två till denna summa och sedan delar med två, får du antalet totala broar plus en. Detta nummer är detsamma som det som användes tidigare, vilket används för att berätta om en sökväg är möjlig. Om alla siffror är jämna, kommer den tredje kolumnen i tabellen att summera till en mindre än det totala antalet broar plus en.

Euler förklarar då att det är uppenbart att om det finns två landmassor med ett udda antal broar så kommer resan alltid att vara möjlig om resan börjar i en av regionerna med ett udda antal broar. Detta beror på att om de jämna siffrorna halveras och var och en av de udda ökas med en och halveras, kommer summan av dessa halvor att motsvara en mer än det totala antalet broar. Men om det finns fyra eller fler landmassor med ett udda antal broar, är det omöjligt att det finns en väg. Detta beror på att summan av halvorna av de udda talen plus en tillsammans med summan av alla halvorna av de jämna talen kommer att göra summan av den tredje kolumnen större än det totala antalet broar plus en. Därför bevisade Euler bara att det kan finnas högst två landmassor med ett udda antal broar.

med detta påpekat kan Euler nu dra sina slutsatser om mer allmänna former av K. I punkt 20 ger Euler de tre riktlinjer som någon kan använda för att ta reda på om det finns en väg med varje bro en gång och bara en gång. Först hävdade han om det finns mer än två landmassor med ett udda antal broar, då är ingen sådan resa möjlig. För det andra, om antalet broar är udda för exakt två landmassor, är resan möjlig om den börjar i en av de två udda numrerade landmassorna. Slutligen säger Euler att om det inte finns några regioner med ett udda antal landmassor kan resan genomföras från och med vilken region som helst. Efter att ha angett dessa tre fakta avslutar Euler sitt bevis med punkt 21, som helt enkelt säger att efter att man räknar ut att en väg finns, måste de fortfarande gå igenom ansträngningen att skriva ut en väg som fungerar. Euler trodde att metoden för att uppnå detta var trivial, och han ville inte spendera mycket tid på det. Euler föreslog emellertid att koncentrera sig på hur man kommer från en landmassa till den andra, istället för att koncentrera sig på de specifika broarna först.

Eulers bevis-och grafteori

När man läser Eulers ursprungliga bevis upptäcker man ett relativt enkelt och lättförståeligt matematikarbete; det är dock inte det faktiska beviset utan de mellanliggande stegen som gör detta problem känt. Eulers stora innovation var att titta på K Kubnigsberg bridge-problemet abstrakt, genom att använda linjer och bokstäver för att representera den större situationen för landmassor och broar. Han använde stora bokstäver för att representera landmassor och små bokstäver för att representera broar. Detta var en helt ny typ av tänkande för tiden, och i hans papper utlöste Euler av misstag en ny gren av matematik som heter grafteori, där en graf helt enkelt är en samling hörn och kanter. Idag kallas en väg i en graf, som innehåller varje kant av grafen en gång och bara en gång, en Eulerisk väg på grund av detta problem. Från det att Euler löste detta problem till idag har grafteori blivit en viktig gren av matematiken, som styr grunden för vårt tänkande om nätverk.

k-Kubnigsberg Bridge-problemet är varför Biggs säger,

ursprunget till grafteori är ödmjuka, till och med oseriösa … problemen som ledde till utvecklingen av grafteori var ofta lite mer än pussel, utformade för att testa uppfinningsrikedom snarare än stimulera fantasin. Men trots den uppenbara trivialiteten hos sådana pussel fångade de matematikernas intresse, vilket resulterade i att grafteori har blivit ett ämne rikt på teoretiska resultat av en överraskande variation och djup.

som Biggs uttalande skulle innebära är detta problem så viktigt att det nämns i det första kapitlet i varje Grafteoribok som granskades i biblioteket.efter Eulers upptäckt (eller uppfinning, beroende på hur läsaren ser på det) blomstrade grafteorin med stora bidrag från stora matematiker som Augustin Cauchy, William Hamilton, Arthur Cayley, Gustav Kirchhoff och George Polya. Dessa män bidrog alla till att avslöja ” nästan allt som är känt om stora men ordnade grafer, såsom gitteret bildat av atomer i en kristall eller det sexkantiga gitteret som gjordes av bin i en bikupa .”Andra kända grafteoriproblem inkluderar att hitta ett sätt att fly från en labyrint eller labyrint, eller hitta ordningen med rörelser med en riddare på ett schackbräde så att varje torg landas på bara en gång och riddaren återvänder till det utrymme som han började . Några andra grafteoriproblem har blivit olösta i århundraden .

ödet för K Jacobnigsberg

medan grafteorin blomstrade efter att Euler löste problemet med K Jacobnigsberg-bron, hade staden K Jacobnigsberg ett mycket annat öde. År 1875 beslutade folket i K Kubnigsberg att bygga en ny bro mellan noderna B och C, vilket ökade antalet länkar i dessa två landmassor till fyra. Detta innebar att endast två landmassor hade ett udda antal länkar, vilket gav en ganska enkel lösning på problemet. Skapandet av den extra bron kan eller kanske inte ha orsakats omedvetet av önskan om en väg för att lösa stadens berömda problem.

en ny bro löste dock inte alla K. S. C. I. S. A., eftersom staden inte förväntade sig tillbaka på nittonde århundradet, ”det sorgliga och krigshärjade ödet som väntade på det som värd för en av de hårdaste striderna under andra världskriget.”Under fyra dagar i augusti 1944 förstörde brittiska bombplan både Gamla stan och de norra delarna av K. I januari och februari 1945 är regionen kring K Jacobnigsberg omgiven av ryska styrkor. Tyska civila börjar evakuera från staden, men flyttar för sent. Tusentals människor dödas och försöker fly med båt och till fots över det iskalla vattnet i den Kuriska lagunen. I April 1945 fångar Red Army K Kubnigsberg med cirka nittio procent av Gamla Stan som ligger i ruiner.

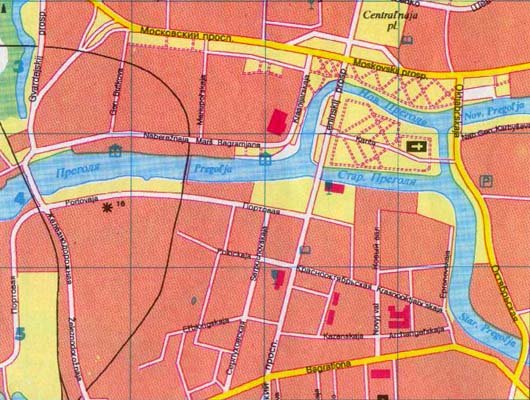
en aktuell gatukarta över K Jacobnigsberg finns nedan . Denna karta visar hur mycket Staden har förändrats. Många av broarna förstördes under bombningarna, och staden kan inte längre ställa samma spännande fråga som de kunde på sjuttonhundratalet. Tillsammans med en mycket annorlunda layout har staden K Kubnigsberg ett nytt namn, Kaliningrad, med floden Pregel bytt namn till Pregolya . Medan ödet för K Kubnigsberg är hemskt, medborgarnas gamla kaffehus problem med att korsa var och en av sina gamla sju broar exakt en gång ledde till bildandet av en helt ny gren av matematik, grafteori.

Biggs, Norman L., E. K. Lloyd och Robin J. Wilson. Grafteori: 1736-1936. Oxford: Clarendon Press, 1976.

Dunham, William. Euler: mästaren av oss alla. Washington: Den matematiska Föreningen i Amerika, 1999.

Euler, Leonhard, ’ Solutio problematis ad geometriam situs pertinentis ’(1741), Enestr Ubicm 53, Maa Euler Arkiv.

” matematikens historia: på Leonhard Euler (1707-1783).”ScienceWeek (2003). 6 Nov. 2005.

Hopkins, Brian och Robin Wilson. ”Sanningen om K Jacobnigsberg.”College Mathematics Journal (2004), 35, 198-207.

”Konigsberg broar.”MacTutor Historia Matematik Arkiv:
http://www-history.mcs.st – and.ac.uk/history/Miscellaneous/other_links/Konigsberg.html

Redaktörens anteckning: Denna artikel publicerades ursprungligen i konvergens, Volym 3 (2006).