De fyra Färgteoremen
de fyra Färgförmodan uttalades först drygt 150 yearsago, och slutligen visade sig slutgiltigt 1976. Det är ett enastående exempel på hur gamla ideer kombineras med nya upptäckter och tekniker inom olika områden av matematik för att ge nya tillvägagångssätt till ett problem. Det är också ett exempel på hur ett uppenbart enkelt problem ansågs vara ’löst’ men blev sedan merkomplex, och det är det första spektakulära exemplet där en dator var involverad i att bevisa en matematisk sats.
I början
antagandet att en karta kunde färgas med endast fyra färger uppträdde först i ett brev frånaugustus De Morgan (1806-1871), första professor i matematik vidden nya Högskolan London, till sin vän William RowanHamilton (1805-1865) den berömda irländska matematikern 1852. Det hadbeen föreslog De Morgan av en av hans elever, FrederikGuthrie, på uppdrag av sin äldre bror Francis (som senare blevprofessor i matematik vid University of Cape Town).


Augustus De Morgan (1807-1871) ochwilliam Rowan Hamilton (1805-1865)
problemet, så enkelt beskrivet, men så tantalizingly svårtatt bevisa, fångade fantasin hos många matematiker vidtid. I slutet av 1860-talet tog de Morgan till och med problemet och hansproof till Amerika där bland annat Benjamin Peirce (1809-1880) känd matematiker och astronom blev intresserad av det som bort för att utveckla sina logiska metoder.
De Morgan använde det faktum att i en karta med fyra regioner, varderarör de andra tre, en av dem är helt omsluten avandra. Eftersom han inte kunde hitta ett sätt att bevisa detta, använde han detsom ett axiom , grunden förhans bevis.
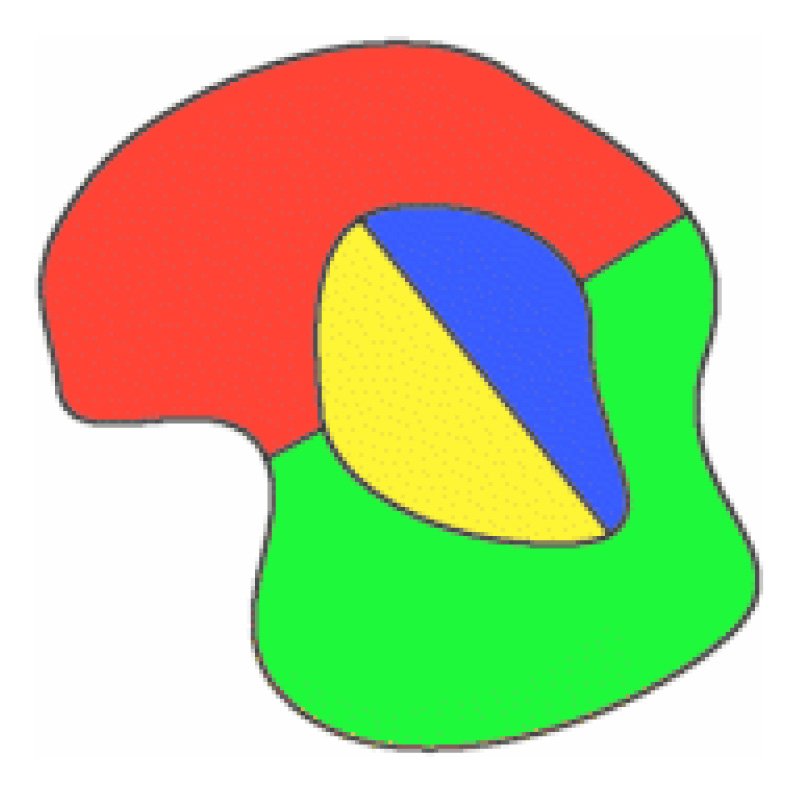
en kopia av De Morgans originalsketch i sitt brev till Hamilton och en enkel fyrfärgskarta.
1878 Arthur Cayley (1821-1895) vid ett möte i Londonmatematiska samhället frågade om någon hade hittat en lösning forDe Morgans ursprungliga fråga, men även om det hade funnits någraintresse hade ingen gjort några betydande framsteg. Cayley blevintresserad av problemet och publicerade 1879 ett kort papperpå färgningen av kartordär han förklarade några av svårigheterna att försöka bevisa och gjorde några viktiga bidrag till hur problemet varnärmade sig. Hans fråga: ’om en viss karta redan är framgångsrikt färgad med fyra färger,och vi lägger till ett annat område, kan vi fortfarande behålla samma färg?’började en annan linje ofenquiry som ledde till tillämpningen av matematicalinduction till problemet.

Arthur Cayley (1821-1895)
Arthur Cayley visade att om fyra färger redan hade använts för att färga en karta, och en ny region lades till, var det inte alltid möjligt att behålla originalfärgen.
ovan har alla fyra färgerna använts på originalkartan, och anew region dras för att omge den. I det här fallet är en röd regionändras till blått, så att rött kan användas på den nya omgivningenregion.
Cayley observerade också att det var möjligt att lösa en version avProblemet genom att begränsa hur gränserna möttes. Till exempel, kartor där bara tre länder träffades har tre kanter möte på avertex. Dessa kallas ’kubiska kartor’, och kartorna som används iföljande diskussion är alla kubiska kartor. Om en karta kan färgas med fyra färger visas bara tre färger på gränsen.
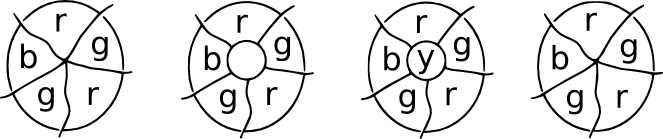
Patchdemonstrationen. Föreställ dig detpå någon plats i en karta möts ett antal länder vid en punkt. Lägg nu en lapp över mötesplatsen, och alla nya mötesplatserkommer att ha tre gränser som härrör från dem. Dessa är kubiska kartor, och en fjärde färg kan användas för den centrala regionen. Vid borttagning av plåstret kan vi återgå till den ursprungliga färgen.
några gamla tekniker, nya förhållanden och fler problem!
För att följa utvecklingen av problemet måste vi undersöka kortfattat några av de ideer, förfaranden och tekniker som matematiker utvecklade i sina försök att lösa det.
de enda fem grannarnas gissning
’ Om du inte kan lösa apartikulära problem, hitta en enklare som du kan lösa.'(Polya. Hur man löser det)
’varje karta har minst ett land med fem eller färre grannar.’
Föreställ dig en karta över en ö omgiven av havet. Ifärgning av länderna på ön räknar vi havet som enregion. Vissa länder kan ha endast två gränser (en digon), sometre (som i en triangel), några Fyra (en kvadrat) och några fem (apentagon) eller mer.
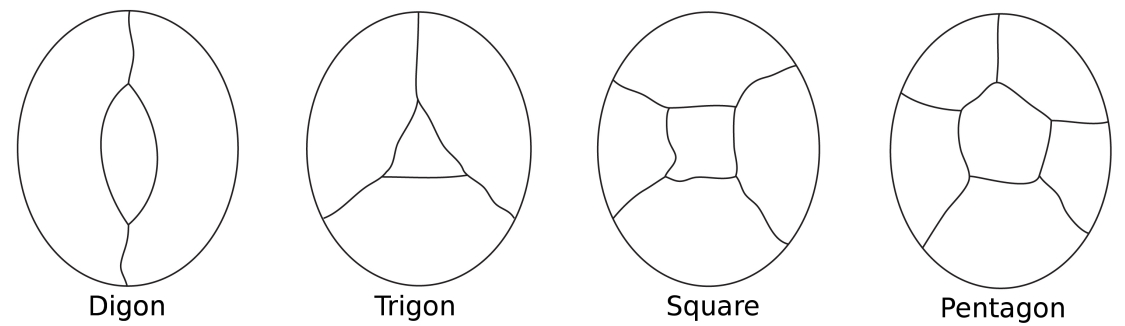
de enklaste möjliga konfigurationerna för att omge en central region.
Observera att i alla dessa konfigurationer har varje nod bara trekantar.
år 1813 anpassades Eulers formel för polyeder för två dimensioner av Augustin Cauchy (1759-1857) genom att projicera polyedern på ett plan som sålunda bildar nätet avsolid. På detta sätt blev formeln $f + v – E = 1$, eftersomcauchy räknade inte ’utanför’ regionen på nätet.

Augustin Cauchy (1759-1857)
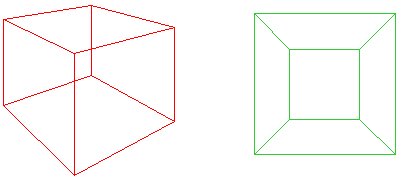
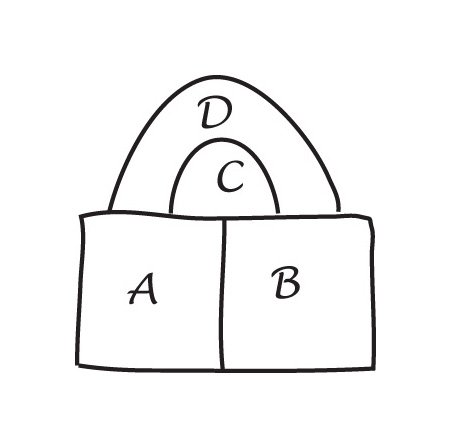
tänk dig att krossa den röda kuben nertill ett plan så att dess bas öppnas ut för att bilda det yttre kanten av det gröna nätet. Cauchys ide var att skära ut ett ansikte avkuben, så att för en planpolygon, $f + v – e = 1$. Alternativt,om ’utsidan’ av nätet betraktas som ett ansikte med infinitearea, har vi fortfarande $f + v – e = 2$
Vi kan anta att det finns minst tre gränslinjer (kanter)som kommer från varje mötesplats (hörn).
beviset på att kartan har minst ett land omgivet av fem eller färre grannar fortsätter av motsägelse. Om detta leder till en absurditet har vi ett bevis.
lägg nu dessa värden i Eulers formel: $$f + v – e = 2$$ ochVi har $$1/3(e) + 2/3(e) – E$$ vilket är noll!
detta är absurditeten, så vårt ursprungliga antagande var falskt.Det betyder att det måste finnas minst ett land med fem eller färre grannar!
minimala brottslingar!
ett annat sätt att ta itu med fyra färgproblem är att anta att det isfalse, och se vart detta leder. Antag att det finns kartor som behöverfem färger eller mer, och vi väljer kartorna med det minstamöjligt antal länder. Dessa kartor kallas minimala motexempel ellerminimala brottslingar !
så det betyder att en minimal brottsling inte kan färgas med fyra färger,men en karta med färre länder kan färgas med fyra färger. Om vi kan visa att minimala brottslingar inte kan existera, kan vi kanske göra vissa framsteg.
Vi kan till exempel visa att en minimal brottsling inte kan innehålla digon.
från den ursprungliga kartan, ta bort en gräns från digon, ochvi får en ny karta med färre länder. Denna karta kan färgasmed Fyra färger (från vårt antagande). Vi färgar sedan denna newmap, (vi behöver bara två färger). Byt nu ut gränsen som vi tog bort och färga kartan igen. Vi har använt tre färger, och eftersom det fortfarande finns ytterligare en färg tillgänglig visar detta att vår karta kan färgas med fyra färger. Men det här är emot vårt antagande, så en minimal brottsling kan inteinnehåller en digon.
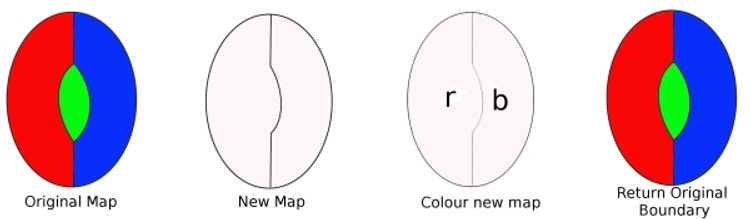
för att visa att en Minimal Kriminellkan inte innehålla en region med två kanter (en digon). Antag att det finnsen minimal brottsling som innehåller en digon. Att ta bort ett kantmedelkartan innehåller färre regioner. Så den här nya kartan kan färgasmed Fyra färger. Byt nu ut den förlorade kanten. Eftersom endast två färger behövdes tidigare innebär byte av kant att vi kan använda atredje färg och fortfarande har en fjärde färg att använda. Så, en minimalkriminell kan färgas med fyra färger. Därför kan en minimalkriminell inte innehålla en digon.
denna procedur kan upprepas för att visa att en minimal kriminellkan inte innehålla ett tresidigt land (en trigon), men det bryts nednär vi försöker tekniken på en kvadrat, för när vi byter utkvadrat kan länderna bredvid det väl använda alla fyrafärger, så bevisförfarandet misslyckas. När detta har hänt blir det uppenbart att det inte fungerar för pentagoner, och så vidare.
de sex Färgteorem
en liknande teknik kan tillämpas för att visa att de sex färgteorem är sant. Först antar vi att det inte finns några kartor som kan färgas med sex färger. Några av kartorna kan färgas med sju färger, så att välja en av dessa (en minimal brottsling), om vi kan visa att det är möjligt att färga det med mindre än sjufärger, har vi uppnått vårt mål.
från proof of the five neighbors theorem är det möjligt att fortsätta använda minimal criminal idea för att visa att en karta kan färgas med sex färger!
från regioner till knutar, nätverk och topologi
1879 Alfred Kempe (1849-1922), med hjälp av tekniker som liknar de ovan beskrivna, startade från egenskapen ’fem grannar ’och utvecklade ett förfarande som kallas metoden för’ Kempe kedjor ’ för att hitta ett bevis på fyra Färgteorem. Han publicerade detta bevis iAmerikansk tidskrift för matematik. Han hittade två enklare versionersom publicerades nästa år, och hans bevis stod i tio år innan Percy Heawood (1861-1955) visade att det fanns ett viktigt fel i bevismetoden som Kempe hade använt.


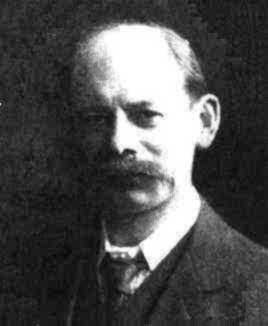
Alfred Kempe (1849-1922), PeterGuthrie Tait (1831-1901) och Percy heawood (1861-1955)
1880 P. G. tait (1831-1901) en matematisk fysiker, erbjudenen lösning på problemet. Oberoende, Tait hade fastställt attkartor där ett jämnt antal gränslinjer möts vid varje punkt,kunde färgas med två färger, även om detta resultat hade dykt upp tidigare i Kempes papper.
under 1876-77 blev Tait känd för sin studie ochklassificering av knutar. Vid den tiden fanns ett antalolika teorier om atomernas struktur. William Thompson (senare Lord Kelvin 1824-1907) inspirerad av experimenten fråntysk fysiker Hermann von Helmholtz (1821-1894) föreslog ateori att atomer var knutna rör av eter. Kelvins teori om’ vortexatomer ’ togs på allvar i ungefär tjugo år, och det inspirerade Tait att göra en klassificering av knutar. Tait, Thomsonoch James Clark Maxwell (1831-1879) uppfann många topologiska ideerunder sina studier. Kelvins teori var dock grundläggandemisstagna och fysiker förlorade intresse för Taits arbete.


Hermann von Helmholtz (1821-1879),Lord Kelvin (1824-1907) och James Clark Maxwell (1831-1879)

tait började med de sätt på vilka en enda sluten slinga av sladden kunde knytas. Han hade ingen systematiskmetod i början och började på ett intuitivt sätt genom att ta en enda sluten slinga och experimentera med hur den kunde knytas. Naturligtvis måste sladden vara öppen (som ashoelace) sedan knuten och förenad. Observera att om du följer thecord runt knuten, kommer ’över – under’ korsningar alternera.Han fortsatte sedan med att experimentera med två slingor och hur de kunde knytas ihop. Här visas knutar med upp till sexkorsningar för en enda slinga.
ett av resultaten av Taits studie var hans Hamiltonian graph conjecture.
en karta betraktas som en polyeder ritad på en sfär, och den kan sedan projiceras på ett plan. Tait föreslog att någon kubikpolyhedral karta har en Hamiltoniancycle . Taits metod fokuserade på kanterna på grafen ochhan visade att en Hamiltonian cykel kunde producera en fyrfärg aven karta. Det var inte förrän 1946 som William Tutte (1917-2002) hittade det första motexemplet till Taits gissning.
Tait och sambandet med knutar
Taitinitierade studien av snarks 1880, när han bevisade att fourcolour-satsen motsvarade uttalandet att ingen snark isplanar. En plan graf är en som kan dras i planet medinga kanter korsar. Det ser ut som om Taits uppfattning om icke-plana grafer har kommit från hans studie av knutar och Hamiltonian vägar .
den första kända snark var Petersen grafen upptäcktes 1898, och matematiker började jaga efter fler av dessa typer av grafermen det var inte förrän 1946 att en annan snark hittades.
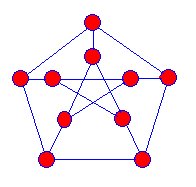 |
SNARKs är projektioner av tredimensionella grafer på theplane. Det finns inga hörn där de blå kanterna verkar korsavarandra. Snarks har följande egenskaper:
|
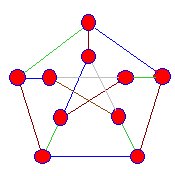 |
kanterna som möter hörn av denna snark är färgade blå,grön och brun, men vi når alltid ett stadium där denna processkan inte fortsätta. |
Julius Peterson (1839-1910)
the hunting of thesnark är en dikt skriven av Lewis Carroll, och Martin gardnernamngivna dessa grafer SNARKs, eftersom de var så svårfångade.
omvandla problemet och hitta nya metoder.
Även om Heawood hittade den stora bristen i Kempes bevismetod 1890 kunde han inte fortsätta bevisa fyra färgteorem, men han gjorde ett betydande genombrott och bevisade slutgiltigt att alla kartor kunde färgas med fem färger.
Heawood gjorde många viktiga bidrag till problemet och flyttade uppmärksamheten från områdena på en karta till gränserna mellan dem. År 1898 hade han bevisat att om antalet kanter runt varje region är delbart med 3 så kunde regionerna färgas med fyra färger.Cauchys bevis på Eulers formel inkluderade också tanken attvilket nät av en polyeder som helst kan trianguleras genom att lägga kanter till makenon-triangulära ansikten i trianglar. Han utvecklade sedan ett förfarande där han raderade kanterna en efter en och visade att Euler ’ sformula kunde bibehållas vid varje steg.
Cauchys bevis på Eulers formel
Cauchys 1813-bevis på Eulers formel började med tanken på aprojektion av en polyeder för att erhålla ett plannät. Han visade vidare (a) att något nät kunde trianguleras, och hans bevis(b) av Eulers formel accepterades vid den tiden.
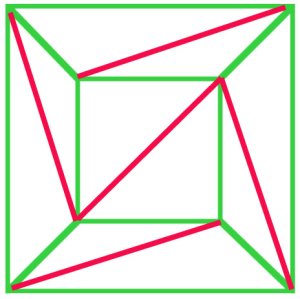 (a)
|
In principle, every polygonal net can be triangulated. In thisnet of a cube (a), $f + v – e$ is $10 + 8 – 17 = 1$, and Euler’sformula still holds. |
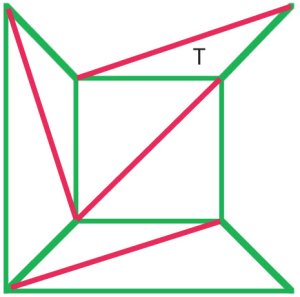 (b)
|
Cauchys argument var att ta bort de yttre kanterna från diagrammet(a) en efter en, och när han nådde ett stadium som i diagrammet (b)bort hela triangeln t, vilket bevarar Eulers formel. Mångamatematiker i början av nittonde århundradet kom överens om att dettaproceduren visade ett bevis på Eulers formel för allpolyhedra. |
vid 1900 visste matematiker att en plan graf kan varakonstruerad från vilken karta som helst med det kraftfulla begreppet dualitet . I dubbelregionerna representeras av hörn och två hörn förenas aven kant om regionerna ligger intill. I dessa grafer frågar FourColour-gissningen nu om grafens hörn kan färgas med 4 färger så att inga två intilliggande hörn är samma färg.
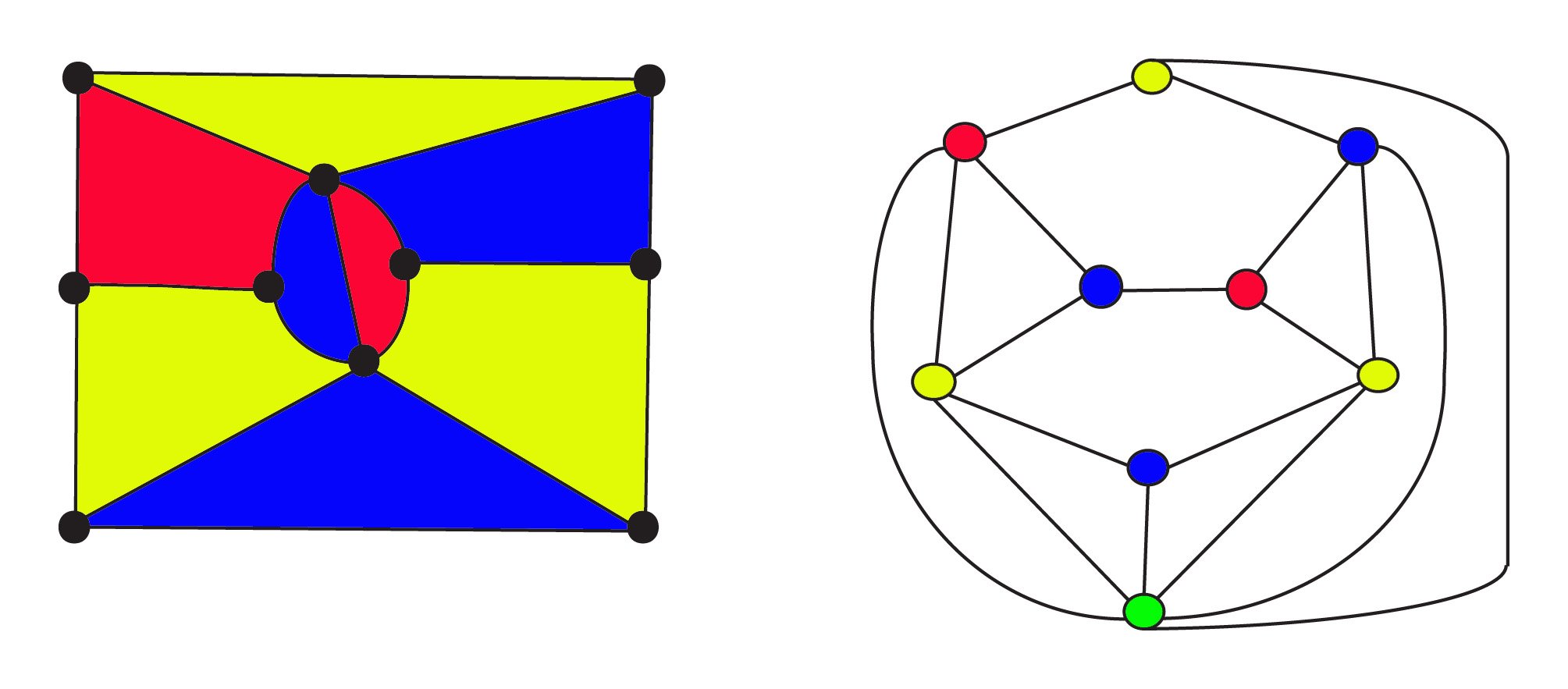
den 3-färgade kartan till vänster har$8$ regioner $10$ hörn och $17$ kanter. Dess dubbla graf på theright har$ 9 $ regioner $9$ hörn och $ 17 $ kanter där hörn är färgade på samma sätt som områdena på kartan. Greenvertex längst ner i diagrammet representerar det oändliga externa området för kartan. Både den ursprungliga kartan och dess dubbla lyda Euler ’ sformula för nätverk $f + v – e = 1$ eller, $\text{regioner} + \text{hörn} – \text{kanter} = 1$. Dualitetsförhållandet ärsymmetrisk: dubbla av dubbla kommer att vara den ursprungliga grafen, därregioner och hörn utbyts.
under första hälften av nittonhundratalet fokuserade matematiker på att modifiera dessa typer av tekniker för att reducerakomplicerade kartor till speciella fall som kunde identifieras och klassificeras, för att undersöka deras speciella egenskaper och utvecklade tanken på en minimal uppsättning kartkonfigurationer som kunde testas.
i första hand ansågs uppsättningen innehålla nästan 9 000 medlemmar vilket var en enorm uppgift, och så matematikernavände sig till datortekniker för att skriva algoritmer som kunde göra testet för dem. Algoritmerna använde modifierade versioner av Kempe ’ soriginal idea of chains tillsammans med andra tekniker för att minskaantalet medlemmar av den minimala uppsättningen.efter att ha samarbetat med John Koch om problemet medreducerbarhet, 1976 vid University of Illinois, reducerade Kenneth Appeland Wolfgang Haken så småningom testproblemet till enunavoidable uppsättning med 1 936 konfigurationer, och en fullständig lösning till de fyra Färgförmodan uppnåddes. Detta problem avkontrollera kartornas reducerbarhet en efter en kontrollerades dubbelmed olika program och olika datorer. Deras bevis visade att minst en karta med minsta möjliga antal regioner som kräver fem färger inte kan existera.
sedan det första beviset har effektivare algoritmer hittats för 4-färgkartor och 1994 hade den oundvikliga uppsättningen avkonfigurationer reducerats till 633.
är ett ’bevis’ gjort på en dator ett korrekt bevis?
eftersom beviset gjordes med hjälp av en dator fanns det ett omedelbart skrik. Många matematiker och filosofer hävdadeatt beviset inte var legitimt. Vissa sa att bevis endast skulle ’bevisas’ av människor, inte maskiner, medan andra av ett mer praktiskt sinne ifrågasatte tillförlitligheten hos båda algoritmerna och maskinernas förmåga att utföra dem utan fel.Men många av de bevis som skrivits av matematiker har varitfann vara felaktiga, så argumentet om tillförlitlighet verkar tomt.Oavsett de yttranden som framförts gav situationen en allvarlig diskussion om bevisets natur som fortfarande fortgåridag.
för pedagogiska anteckningar:
Använd fliken anteckningar högst upp i den här artikeln eller klicka här .
anteckningar
- mer detaljer om detta och de andra procedurerna som finns i detta avsnitt kan ses i Robin Wilsons bok Fyra färger räcker .
- knutar kan vara vänsterhänt eller högerhänt, och idag finns detviktiga tillämpningar av denna egenskap inom kemi, apotek,biologi och fysik. (Se pedagogiska anteckningar)
- uppkallad efter William Rowan Hamilton (1805-1865). En Hamiltonian väg i ett grafbesökvarje toppunkt exakt en gång. En Hamiltonian cykel (eller krets) är apath som besöker varje vertex exakt en gång och återgår tillstartar vertex.(Se pedagogiska anteckningar)
- boken av Imre Lakatos, bevis och Refutations har endiskussion och kritik av Cauchys förfarande (sidorna 6 – 12) och mycket mer om historien om Eulers Sats.
- tanken om dualitet uppstod under 16 och 17 århundraden medutveckling i projektiv geometri. Matematiker som Pascal andDesargues fann att nya satser kunde hittas genom att utbyta termerna ’punkt’ och ’linje’ i beskrivningar av vissa geometriskakonfigurationer. Ett exempel är i vanlig polyhedra, därvertices av en motsvarar ansikten på den andra. Så dualof en tetraeder är en annan tetraeder, och den dubbla av en kub ären oktaeder. Den dubbla av den dubbla är originaletpolyhedron.
den allra bästa populära, lättlästa boken om fyra ColourTheorem är:
Wilson, R. (2003)
Fyra färger räcker.
London. Pingvin Böcker.
för en mer detaljerad och teknisk historia är standardreferensboken:
Biggs, n.; Lloyd, E. &Wilson, R. (1986) (1998)
grafteori,1736-1936
Oxford. Oxford University Press.
den här ger oss uppdaterade, med nyare grundvalar och filosofi.
Fritsch, R och Fritsch, G (2000)
Four Color Theorem: historia,topologiska fundament och Idea of Proof
New York. Springer-Verlag.
knappast någon allmän historiebok har mycket om ämnet, men det sista kapitlet i Katz som heter ’datorer och applikationer’ har asektion om grafteori, och fyra Färgteorem nämns två gånger.
Polya G. Hur man löser det.
det här är den klassiska boken om problemlösning. Det har varitMånga utgåvor av den här boken sedan den först dök upp på 1950-talet ochDet är fortfarande lätt tillgängligt. Märkligt nog har de senaste utgåvorna varitges undertexten ’en ny aspekt av matematisk metod’.
Lakatos, I. (1976) bevis ochrefutationer: logiken för matematisk upptäckt.
Cambridge. C. U. P.
Detta är en annan viktig bok som ledde till forskning om problemlösning och undersökningar på 1970-talet. Det börjar som en klassrumsdiskussion mellan en lärare och en grupp studenter om beviset på Eulers formel och sträcker sig genom de tankar, invändningar och möjligheter som faktiskt diskuterades avmatematiker och forskare under nittonde århundradet. Det lyfter upp några av de viktigaste frågorna om undervisning och lärande problemlösning och om matematiska metoder och bevis.
relaterade referenser
Jag har haft en liten bok om Strängspel under en tid. När jag var i skolan kallades det kattens vagga, och vi spelade det i vårbreak tid.
nyligen har en fransk tidskrift publicerat ett papper om’ algebra ’ av strängfigurer! Om du går till Amazon hittar du anice-bok av Ann Swain och Michael Taylor som heter Finger Strings: A Book of Cats Cradles andString Figures som ska publiceras av Floris books I September2008. Det finns cirka 80 figurer beskrivna med färgade diagrams.It är spiral bunden, så det kommer att vara öppen medan du följer instruktionerna. Det kommer också med ett par strängöglor!
För knut experter, AshleyBook av knutar är en klassiker för alla som är intresserade avhundratals olika typer av knutar och deras användning. Amazon harolika utgåvor tillgängliga till olika priser.
webblänkar
för en allmän översikt och länkar till många människor och ämnen är theMacTutor webbplats
och naturligtvis MacTutor biografier av de inblandade iutveckla alla olika matematiska aspekter kan hittas på MacTutor biografier Index.
fyra Färgteorem och tre bevis. Följande webbplats har en spännande ny metod för att angripa problemet med att bygga en ny algoritm för att lösaproblemet och binda för att minska beroendet av en dator.http://www.emu.edu.tr/~cahit/the%20four%20color%20theorem%20—%20three%20proofs.htm
För grafteori ger Wikipedia en bra översikt, och du kanskippa de riktigt tekniska grejerna. Det visar vilka typer av modernaapplikationer av detta område av matematik. Om du går till Graphcoloring och klickar på Four Colour Theorem, så hittar du mycket mer information.
en intressant och inte alltför teknisk historia av knutteori – hur en ide från Kelvins fysik återgår till Atomteoridag.
Föreningen för lärare i matematik har Celtic Knotdesign affischer. Gå till deras hemsida och bläddra i alfabetiskalista över resurser.
ta reda på allt om knutar på Knutatlasen! Om du inte är anexpert-bara njuta av mångfalden och komplexiteten i databasen ”inthe spirit of wiki”
mer konstnärlig och färgstark – men inte mindre matematisk ärknot tomt webbplats.
För dem som vill ha några av de ursprungliga sakerna och historicaldetail gå till historien om knutteori på: