9. Impedans och fasvinkel
missa inte…
utforska impedans, ström och spänning i en RLC-krets i appleten senare på denna sida.
Impedans
impedansen hos en krets är det totala effektiva motståndet mot strömflödet genom en kombination av kretsens element.
Symbol: Z
enheter: ’Kubi’
den totala spänningen över alla 3 element (motstånd, kondensatorer och induktorer) är skriven
VRLC
för att hitta denna totala spänning kan vi inte bara lägga till spänningarna VR, VL och VC.
eftersom VL och VC anses vara imaginära kvantiteter har vi:
Impedans VRLC = iz
So `Z = R + j(X_L− x_c)`
nu ges storleken (storlek eller absolut värde) av Z av:
`|Z/=sqrt(r^2+(X_L-X_C)^2`
fasvinkel
`tan\ theta=(X_L-X_C)/r`
vinkel michai representerar fasvinkeln mellan strömmen och spänningen.
jämför detta med fasvinkeln som vi träffade tidigare i grafer av y = a sin (bx + c).
exempel 1
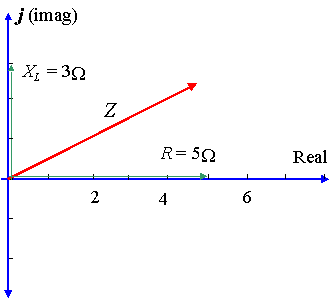
en krets har en resistans på `5\ Kubi` i serie med en reaktans över en induktor på `3\ Kubi’. Representera impedansen med ett komplext tal, i polär form.
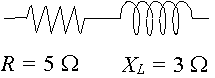
svar
i det här fallet, `x_l= 3\ Kubi` och `x_c= 0` så `x_l – x_c= 3\ Kubi`.
så i rektangulär form är impedansen skriven:
`Z = 5 + 3J\ Jacobs`
med hjälp av kalkylatorn ges storleken på Z av: `5.83`, och vinkeln `kub` (fasskillnaden) ges av: `30.96^@`.
så spänningen leder strömmen med ’ 30.96^@’, som visas i diagrammet.
presenterar Z som ett komplext tal (i polär form), vi har:
`Z = 5,83 20,96 xnumx xnumx xnumx xnumx xnumx xnumx xnumx xnumx xnumx xnumx xnumx xnumx xnumx xnumx xnumx xnumx xnumx xnumx.
exempel 2(a)
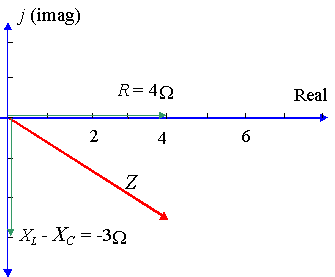
en viss växelströmskrets har ett motstånd på `4\ Jacobs`, en reaktans över en induktor på `8\ Jacobs` och en reaktans över en kondensator på `11\ Jacobs`. Uttryck kretsimpedansen som ett komplext tal i polär form.
svar
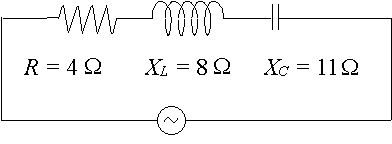
i det här fallet har vi: `X_L – X_C= 8 – 11 = -3\ Kubi `
so` z = 4 – 3J\ Jacobs ’ i rektangulär form.
nu för att uttrycka det i polär form:
med hjälp av kalkylatorn hittar vi `r = 5` och ` kub = -36.87^@`.
So `Z = 5 Ci -36.87^@\ ci`
interaktiv RLC-graf
nedan är en interaktiv graf att spela med (det är inte en statisk bild). Du kan utforska effekten av ett motstånd, kondensator och induktor på total impedans i en växelströmskrets.
aktiviteter för denna interaktiva
- först, bara spela med reglagen. Du kan:
dra den övre reglaget åt vänster eller höger för att variera impedansen på grund av motståndet, `R`,
dra XL-reglaget uppåt eller nedåt för att variera impedansen på grund av induktorn, `X_L` och
dra XC-reglaget uppåt eller nedåt för att variera impedansen på grund av kondensatorn, `X_C`. - observera effekterna av olika impedanser på värdena för XL-XC och Z.
- observera effekterna av olika impedanser på kub, vinkeln som den röda ”resultat” – linjen gör med den horisontella (i radianer).
- Tänk på graferna för spänning och ström i det interaktiva. Observera mängden fördröjning eller bly när du ändrar reglagen.
- Vad har du lärt dig av att spela med denna interaktiva?