Darcys lag är avgörande för att förstå många grenar av geologi, särskilt hydrogeologi. Innan vi tittar på lagen och vad den kan berätta för oss, låt oss titta på hur den utvecklades. Darcy lag är uppkallad efter Henry Darcy, en 19th century fransk ingenjör som utvecklat en underjordisk tryck rörsystem för att leverera vatten runt staden Dijon. Systemet, som också gav vatten till de berömda Dijon fontänerna, revolutionerade stadens vatten-och avloppssystem. Systemet krävde inga pumpar och drevs enbart av tyngdkraften. Under processen att utveckla det nya systemet genomförde Darcy en serie experiment där han försökte flytta vatten enbart med gravitation.

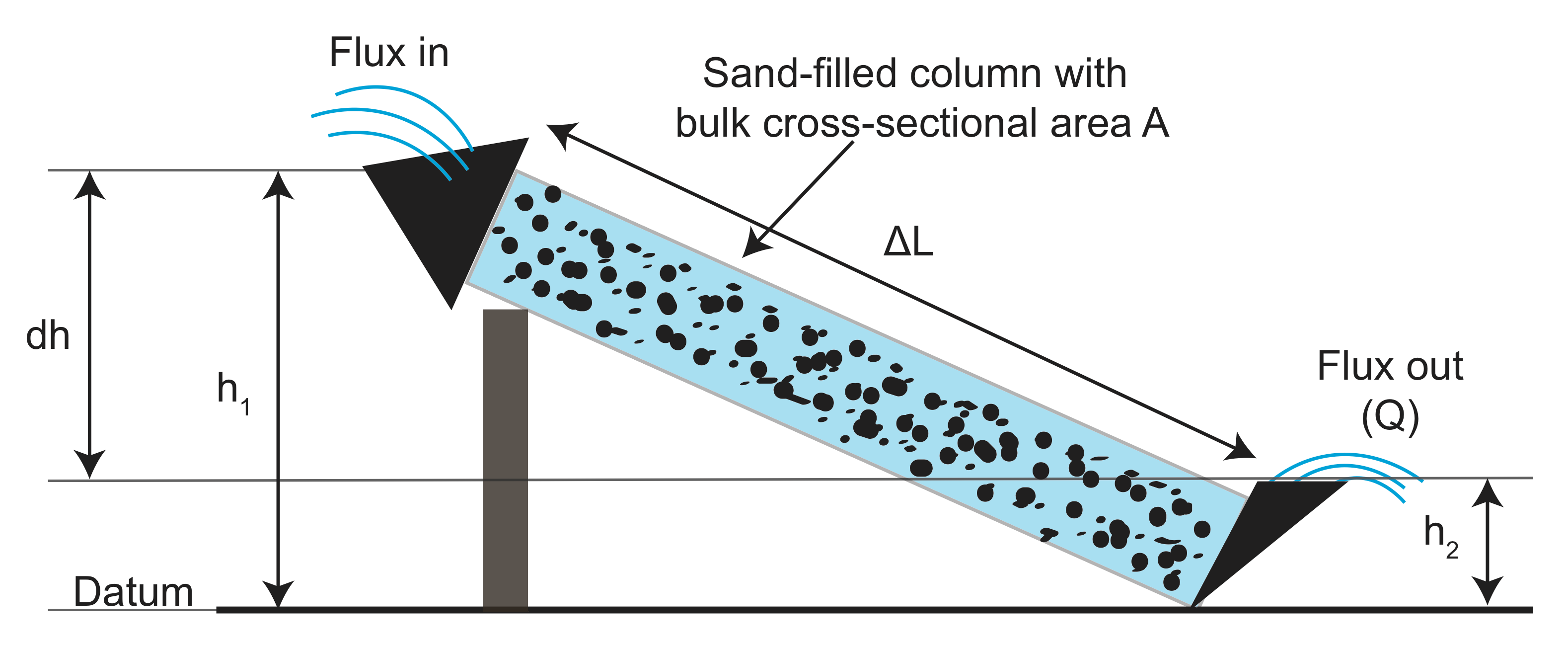
från experimenten, samlade data om längden på flume (\(L\)), tvärsnittsarean på flume (\(A\)), höjdskillnaden (\(h_1 – h_2\)) och flödet av vatten som kommer ut \(Q\) både med och utan granulärt (filtrerande) material i Flume (\(a\)) Flume. Han ritade sedan flödesmätningen normaliserad av området kontra förhållandet mellan höjdskillnaden och längden på flummen (\( \frac{h_1 – h_2}{l}\)). Vad han fann är att det finns ett linjärt förhållande, och lutningen beror på det granulära materialet han använde i flume:

\

som kan skrivas om som ett derivat,

\

där \(K\) är den hydrauliska konduktiviteten och \(\frac{dh}{dx}\) är den hydrauliska gradienten. \(Q\), den totala urladdningshastigheten, har enheter av \(\frac{m^3}{s}\), volymen av vatten per gång. Det negativa tecknet beror på att vätskan strömmar ner (negativ) den hydrauliska gradienten från högre värden till lägre värden.

den hydrauliska ledningsförmågan är en fysisk parameter som redogör för hur lätt vätskan kan röra sig genom porutrymmet för materialet. I Darcys ursprungliga experiment använde han sand med olika kornstorlekar, men den hydrauliska ledningsförmågan kan också bestämmas för fasta stenar, eftersom de flesta stenar har lite porutrymme.efter Darcys ursprungliga experiment gjordes ytterligare arbete för att förstå de fysikaliska egenskaperna hos vätskan och berget som bestämmer den effektiva hydrauliska ledningsförmågan. Från dessa experiment fann man att

\

där \(k\) är den inneboende permeabiliteten hos det porösa mediet (det fasta ämnet), \(\eta\) är vätskans dynamiska viskositet och \(\gamma = \rho g\) är vätskans specifika vikt, vilket beror på vätsketätheten, \(\rho\) och tyngdkraften, \(g\).

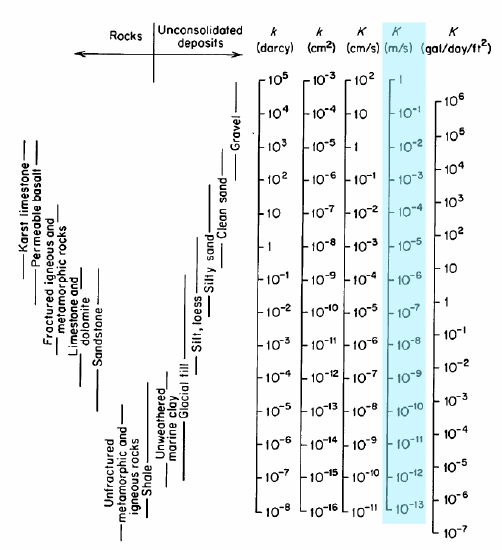
den markerade kolumnen i figuren är K, den hydrauliska ledningsförmågan i \(\frac{m}{s}\); Dessa är de enheter som vi kommer att använda. Den hydrauliska ledningsförmågan rapporteras också ibland i termer av den inneboende permeabiliteten, \(k\), med enheter av darcys eller cm2. Det fullständiga värdet för hydraulisk ledningsförmåga är 1-10-13 \(\frac{m}{s}\). Experiment som Darcys används för att mäta K i verkliga material.

urladdningshastigheten \(q\) är ett volymflöde (\(m^3/s\)), men vi brukar tänka på vätskeflöde i termer av hastighet eller hastighet. Urladdningsfrågorna kan ordnas om genom att dividera genom området för att definiera Darcy-flödet

\\]

eller i termer av den inneboende permeabiliteten och tryckgradienten,

\

där \(\eta\) är vätskeviskositeten (se nedan för härledningen av den andra ekvationen).

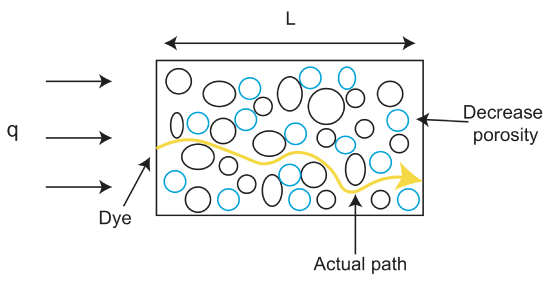
det är viktigt att notera att Darcy-flödet inte motsvarar vätskehastigheten, även om det är i hastighetsenheter. Vätskehastigheten hittas genom den genomsnittliga linjära hastigheten (\(v_a\)), vilket är medelvärdet av hastigheten för alla möjliga vätskevägar genom det porösa mediet: men att hitta detta värde ligger utanför denna klass. Istället noterar vi att vätskehastigheten är

\

där \(\varphi\) är porositeten och v är vätskehastigheten. Porositeten, \(\varphi\) beräknas som förhållandet mellan volymen av tomrum till den totala volymen av ett material \(\varphi=\ frac{V_{void}}{V_{tot}}\), och uttrycks vanligtvis som en fraktion mellan 0 och 1 eller som en procent. Observera att om \(\varphi\leq\)1 då är vätskehastigheten större darcy-flödet.

en annan term som uppstår när man diskuterar flöde genom stenar och okonsoliderade material är permeabilitet. Medan porositet är den faktiska fraktionen av porer (hålrum) i berget, kan dessa hålrum ha olika former och olika anslutningar, vilket påverkar hur lätt en vätska kan röra sig genom porutrymmet. Permeabiliteten är ett mått på hur lätt vätskor och gaser kan passera genom en sten. Ju mer konsoliderat materialet desto lägre är dess permeabilitet. Således har” lösa ” material som grus hög permeabilitet. Vissa stenar kan också ha anisotropisk permeabilitet, vilket innebär att vätskor lätt kan strömma i en riktning, men inte i en annan. Ett exempel på en sten med anisotropisk permeabilitet är en skiffer. Vätskor kan röra sig lätt inom ett lager av skiffer, men kan inte röra sig över lager.

hydrauliskt Huvud

återgå till Darcys experiment, vad är fysisk process som faktiskt driver flödet av vätska genom flummen?

termen \(\frac{dh}{dx} \) kallas det hydrauliska huvudet, vilket är vätsketrycket på grund av vikten av en vätska i förhållande till någon referensplats: en tryckgradient. Men \(\frac{dh}{dx} \) har inte enheter med ett tryck per enhetslängd, så varför kallas det hydraulhuvudet?

låt oss överväga vad trycket är i flume i Darcys experiment. För att göra experimenten hade Darcy en tank med vatten i den övre änden av flume som ger en konstant vattennivå på toppen av flume, motsvarande höjden på flume, \(h_1\). På samma sätt fanns en tank i botten med en konstant vattennivå motsvarande \(h_2\). Därför ges vätsketrycket i var och en av tankarna på grund av vattnets vikt av \(P = \rho G h\). Tryckgradienten mellan plumens topp och botten är då

\

eller

\

ersätter Darcys lag,

\ &=\frac{K}{\rho g}\frac{dp}{dx} \end{align}. \ ]

minns, ovanifrån att den hydrauliska ledningsförmågan kan skrivas i termer av den inneboende permeabiliteten som \(K = K\frac{\gamma}{\eta}\) vilket motsvarar \(k\frac{\rho g}{\eta} \) eller omarrangering, \(\frac{K}{\rho g} = \frac{k}{\eta} \). Därför kan vi ersätta att ge två ekvivalenta uttryck för Darcys lag, med en interms av gradienten i höjd,

\

och den andra i termer av gradienten i tryck,

\

således kallas \(\frac{dh}{dx}\) det hydrauliska huvudet eftersom det fysiska ursprunget för termen i Darcys lag är tryckgradienten i vätskan, som driver flödet.

vatten som lämnar en akvifer

Låt oss nu göra ett exempel som beräknar vätskehastigheten för vatten som kommer in i en akvifer. I skissen under akviferhöjden följer topografin på kullen intill dalen med strömmen. Vatten strömmar från högt tryck (Huvudhöjd) mot dalen och lämnar akvifären vid bäcken. Vi kan använda Darcys lag för att uppskatta vattenflödeshastigheten från akvifären.

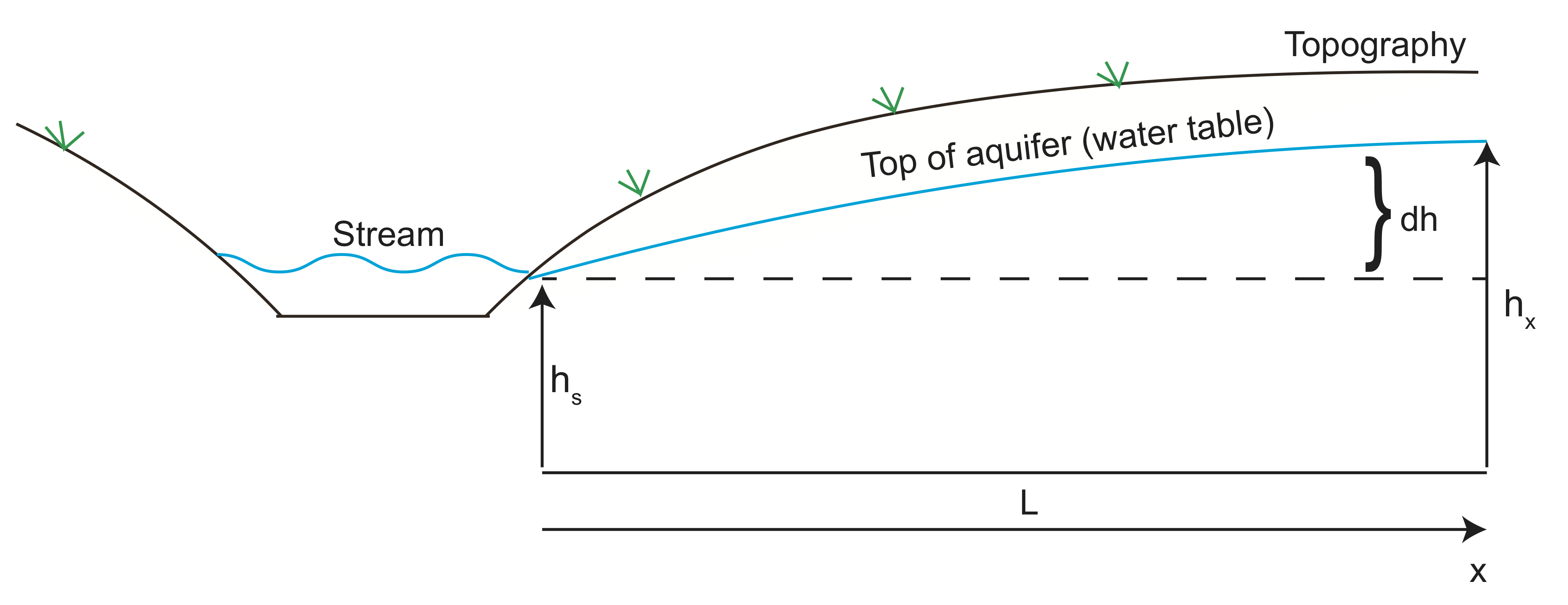
med hjälp av geofysisk avbildning befinns akviferns höjd vara 10 m (\(dh\)) ovanför strömhöjden cirka 100 meter (\(L\)) bort. Antag att den hydrauliska ledningsförmågan är \ (K=10^{-6}\) m/S och porositeten är \(\varphi=30\)%.

Darcy-flödet är

\

\

fluidhastigheten är

\

\

\

\

\

\

laminärt kontra Turbulent flöde

ett av de implicita antagandena i Darcys lag är att flödet är laminärt. Laminärt flöde karakteriseras som bestående av tunna skikt eller laminer av vätska som alla rör sig parallellt med varandra. I kontrast turbulent flöde kännetecknas av virvlar, virvlar och virvlar, i vilka intilliggande lager av vätska divergerar och ta olika vägar ner ström.ett sätt som vi kan kvantifiera om en vätska är laminär eller turbulent är genom att beräkna Reynolds nummer för flödet, definierat som

\

Reynolds nummer hittas genom att överväga de två termerna i momentumbalansen för flödet. Den första termen är tröghetskraften per volymenhet, som driver flödet, \(\rho u\frac{du}{dx}\). Den andra termen är den viskösa kraften per volymenhet, som motstår flöde, \(\eta\frac{d^2U}{dx^2}\). Dessa två termer måste balansera, så vi kan ställa in dem lika,

\

därefter skriver vi om termerna på ett förenklat sätt för att bara fånga de relevanta dimensionerna av variablerna. För att göra det går vi igenom det som kallas en dimensionell analys, där vi ersätter varje variabel, med referensvärden, gånger en icke-dimensionell form av variabeln.

till exempel för termen \(x\) skrivs om som bara \(L x’\), där \(L\) är referenslängden (vätskedjupet) och \(x’\) är det icke-dimensionella avståndet. På samma sätt låter vi \(u = u_o u’\). Genom att ersätta dessa i ekvationen får vi

\

nästa kombinerar vi de konstanta värdena framför

\

Observera att kombinationen av variabler framför är Reynolds nummer

\

där variablerna är \(u_o\) flödeshastighet, l vätskedjup och variablerna vi har sett tidigare, \(\rho\) Vätsketäthet och \(\eta\) vätskeviskositet. Genom att gå igenom denna analys finner vi att varje flöde som kännetecknas av balansen mellan dessa två termer kan jämföras genom att helt enkelt veta värdet på Reynolds nummer. Till exempel, om ett flöde har en viskositet som är 10 gånger viskositeten i ett annat flöde, kommer de två flödena att uppträda samma är densiteten (eller hastigheten eller längden) ökas också med en faktor 10 för det högre viskositetsfallet; det vill säga Reynolds-talet för de två flödena är detsamma.

För att ha Darcy-flöde måste Reynolds nummer vara mindre än cirka 1-10 (laminärt). För \(Re>1-10 \) flödet är inte strikt laminärt, men det är ännu inte turbulent (icke-linjärt, inte laminärt). För att ha turbulent flöde måste Reynolds antal vara större än cirka 2000.

förstå att konstanterna i täljaren och nämnaren påverkar flödets egenskaper på motsatt sätt, hjälper också till att tänka på hur olika vätskor kommer att uppträda under liknande yttre förhållanden. Till exempel, en tätare vätska som också har en snabb hastighet kommer att ha en högre Re och uppvisar turbulent beteende. Däremot kommer en vätska som IS som har en hög viskositet och rör sig mycket långsamt att ha en låg Re och kommer sannolikt att ha laminärt flöde. Isens höga viskositet verkar för att stabilisera flödet. Som ett annat exempel kan två vätskor båda röra sig med samma hastighet bete sig annorlunda om de andra värdena i Reynolds nummer \(\frac{\rho l}{\mu}\) är olika. Därför beror flödestypen inte bara på flödeshastigheten utan på kombinationen av variabler i Reynolds nummer.

tillämpning av Darcys flöde

Darcys lag är huvudekvationen som styr flödet i akviferer och brunnar. Utan det skulle vi inte kunna borra brunnar eller förstå vattenrörelsen i akviferer, särskilt i Kaliforniens central valley, där båda dessa tankar är avgörande för både jordbruksproduktivitet och grundvattensänkning.