Teorema celor Patru culori
conjectura celor patru culori a fost enunțată pentru prima dată puțin peste 150 de ani și, în cele din urmă, s-a dovedit concludent în 1976. Este un exemplu remarcabil al modului în care ideile vechi se combină cu noile descoperiri și tehnici din diferite domenii ale matematicii pentru a oferi noi abordări ale unei probleme. Este, de asemenea, un exemplu al modului în care o problemă aparent simplă a fost considerată a fi ‘rezolvată’, dar apoi a devenit mai complexă și este primul exemplu spectaculos în care un computer a fost implicat în dovedirea unei teoreme matematice.
la început
presupunerea că orice hartă ar putea fi colorată folosind doar patru culori a apărut pentru prima dată într-o scrisoare de la Augustus De Morgan (1806-1871), primul profesor de matematică la new University College London, prietenului său William RowanHamilton (1805-1865) celebrul matematician irlandez în 1852. I-a fost sugerat lui De Morgan de către unul dintre studenții săi, FrederikGuthrie, în numele fratelui său mai mare Francis (care a devenit mai târziu profesor de matematică la Universitatea din Cape Town).


Augustus De Morgan (1807-1871) andWilliam Rowan Hamilton (1805-1865)
problema, deci pur și simplu descris, dar atât de tentant de dificilpentru a dovedi, a prins imaginația multor matematicieni la acel moment. La sfârșitul anilor 1860, De Morgan a dus chiar problema și dovada sa în America, unde, printre altele, Benjamin Peirce (1809-1880) un matematician și astronom celebru, a devenit interesat de ea ca departe de a-și dezvolta metodele logice.
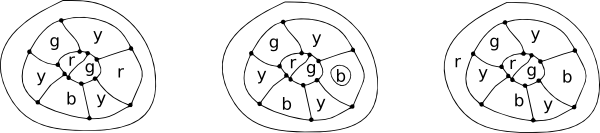
De Morgan a folosit faptul că într-o hartă cu patru regiuni, fiecare atingându-le pe celelalte trei, una dintre ele este complet închisă de celelalte. Din moment ce el nu a putut găsi o modalitate de a dovedi acest lucru, el a folosit-Oca o axiomă , baza dedovada lui.
o copie a originalului lui De Morgan în scrisoarea sa către Hamilton și o hartă simplă în patru culori.
în 1878, Arthur Cayley (1821-1895), la o întâlnire a Societății Matematice din Londra, a întrebat dacă cineva a găsit o soluție pentru întrebarea inițială a lui Morgan, dar, deși au existat unele interese, nimeni nu a făcut progrese semnificative. Cayley a devenit interesat de problemă și în 1879 a publicat o scurtă hârtie despre colorarea hărților, unde a explicat unele dintre dificultățile în încercarea unei dovezi și a adus câteva contribuții importante la modul în care problema a fost abordată. Întrebarea lui este :dacă o anumită hartă este deja colorată cu succes în patru culori și adăugăm o altă zonă,putem păstra aceeași culoare? a început o altă linie de anchetă care a dus la aplicarea inducției matematice la problemă.

Arthur Cayley (1821-1895)
Arthur Cayley a arătat că dacă fourcolours au fost deja folosite pentru a colora o hartă și a fost adăugată o nouă regiune, nu a fost întotdeauna posibilă păstrarea culorii originale.
mai sus, toate cele patru culori au fost folosite pe harta originală, iar o nouă regiune este atrasă să o înconjoare. În acest caz, o regiune roșie esteschimbat în albastru, astfel încât roșu poate fi folosit pe noul împrejurimiregiune.
Cayley a observat, de asemenea, că a fost posibilă rezolvarea unei versiuni a problemei prin restricționarea modului în care limitele s-au întâlnit. De exemplu, hărțile în care s-au întâlnit doar trei țări au trei margini care se întâlnesc la avertex. Acestea se numesc ‘hărți cubice’, iar hărțile utilizate în discuția următoare sunt toate hărți cubice. De asemenea, dacă o hartă poate fi colorată cu patru culori, doar trei culori vor apărea pe graniță.
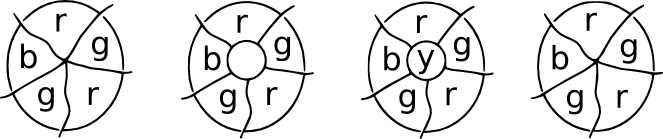
demonstrația de Patch-uri. Imaginați-vă astaîntr-un loc dintr-o hartă, un număr de țări se întâlnesc la un moment dat. Acumpuneți un patch peste punctul de întâlnire și toate noile Puncte de întâlnireva avea trei granițe care emană de la ele. Acestea sunt hărți cubice, iar o a patra culoare poate fi utilizată pentru regiunea centrală. La îndepărtarea plasturelui, putem reveni la culoarea originală.
unele tehnici vechi, noi Condiții și mai multe probleme!
pentru a urmări evoluțiile problemei, trebuie săinvestigăm pe scurt câteva dintre ideile, procedurile și tehnicilecare matematicienii s-au dezvoltat în încercările lor de a o rezolva.
singura conjectură a celor cinci vecini
‘dacă nu puteți rezolva problema aparticulară, găsiți una mai ușoară pe care o puteți rezolva.'(Polya. Cum se rezolvă)
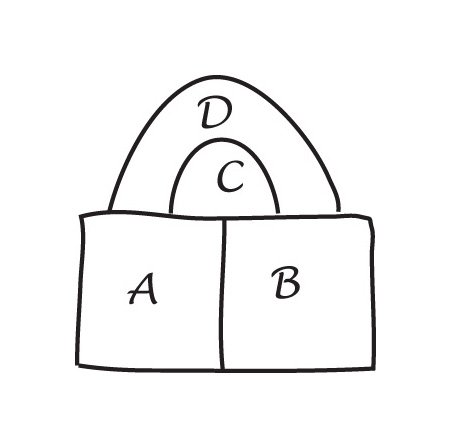
‘fiecare hartă are cel puțin o țară cu cinci sau mai puțini vecini.Imaginați-vă o hartă a unei insule înconjurate de mare. În colorarea țărilor insulei, considerăm Marea ca fiind unaregiune. Unele țări pot avea doar două frontiere (un digon), somethree (ca într-un triunghi), unele Patru (un pătrat) și unele cinci (apentagon) sau mai mult.
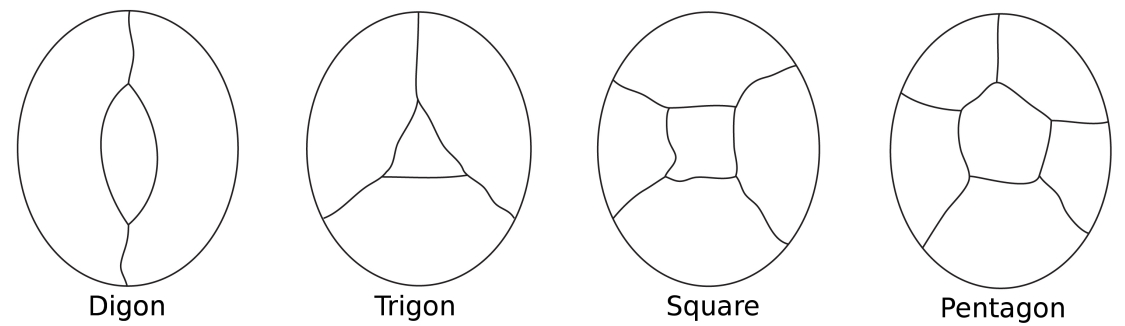
cele mai simple posibile configurații pentru a înconjura o regiune centrală.
rețineți că în toate aceste configurații fiecare nod are doar treimargini.
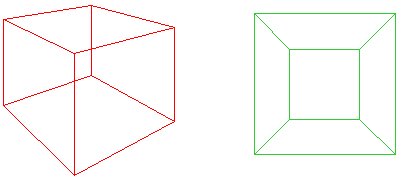
în 1813, formula lui Euler pentru poliedre a fost adaptată pentru două dimensiuni de Augustin Cauchy (1759-1857) prin proiectarea poliedrului pe un plan formând astfel Plasa de solid. În acest fel, formula a devenit $f + v – e = 1$, deoarece kauchy nu a numărat regiunea exterioară a rețelei.

Augustin Cauchy (1759-1857)
imaginați-vă strivirea cubului roșu în jos pe un plan, astfel încât baza sa să fie deschisă pentru a forma marginea exterioară a plasei verzi. Ideea lui Cauchy a fost să taie o față decub, astfel încât pentru un poligon plan, $f + v – e = 1$. Alternativ, dacă ‘exteriorul’ netului este privit ca o față cu infinitearea, atunci mai avem $f + v – E = 2$
putem presupune că există cel puțin trei linii de frontieră (muchii)care ies din fiecare punct de întâlnire (vârfuri).
dovada că harta are cel puțin o țară înconjurată de cinci sau mai puțini vecini se desfășoară prin contradicție. Dacă acest lucru duce la o absurditate, avem o dovadă.
acum puneți aceste valori în formula lui Euler: $$f + v – e = 2$$ și avem $$1/3(e) + 2/3(e) – e$$ care este zero!
aceasta este absurditatea, deci presupunerea noastră inițială a fost falsă.Aceasta înseamnă că trebuie să existe cel puțin o țară cu cinci sau mai puțini vecini!
criminali minime!
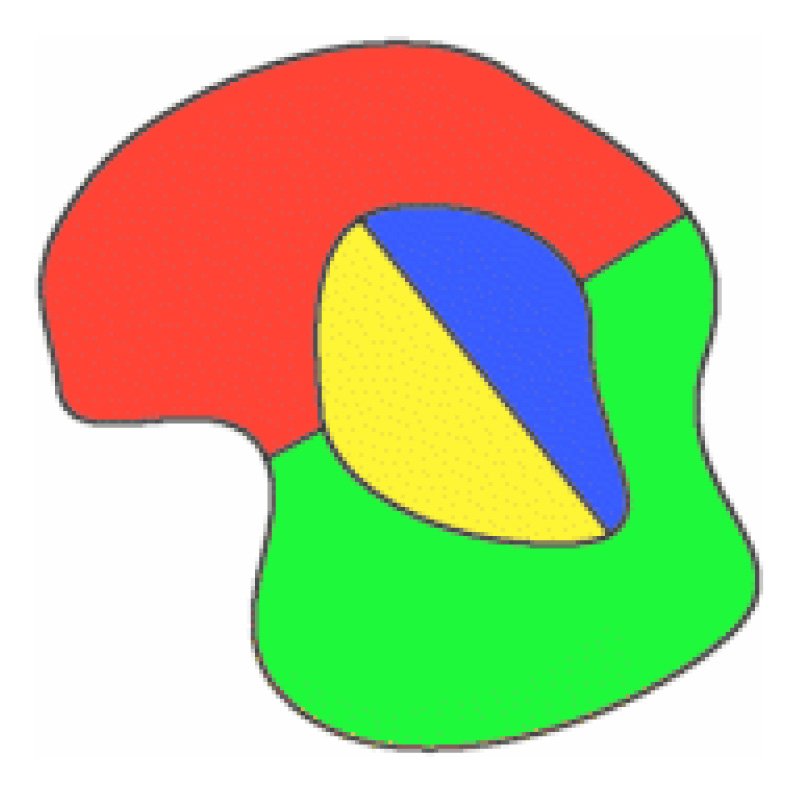
O altă modalitate de a aborda problema celor patru culori este să presupunem că este falsă și să vedem unde duce acest lucru. Să presupunem că există hărți care au nevoie de cinci sau mai multe culori și alegem hărțile cu cel mai mic număr posibil de țări. Aceste hărți sunt numite contra-exemple minime saucriminalii minime !asta înseamnă că un criminal minimal nu poate fi colorat cu patru culori,dar orice hartă cu mai puține țări poate fi colorată cu patru culori. Dacă putem demonstra că infractorii minimali nu pot exista, atunci am putea face unele progrese.
de exemplu, putem arăta că un criminal minim nu poate conține un digon.
din harta originală, scoateți o limită de la digon șiobținem o nouă hartă cu mai puține țări. Această hartă poate fi coloratăcu Patru culori (din presupunerea noastră). Apoi colorăm această hartă nouă (avem nevoie doar de două culori). Acum, înlocuiți granița am eliminat, și re-color Harta. Am folosit trei culori și, din moment ce mai există încă o culoare disponibilă, acest lucru arată că harta noastră poate fi colorată cu patru culori. Dar acest lucru este împotriva presupunerii noastre,astfel încât un criminal minim nu poateconține un digon.
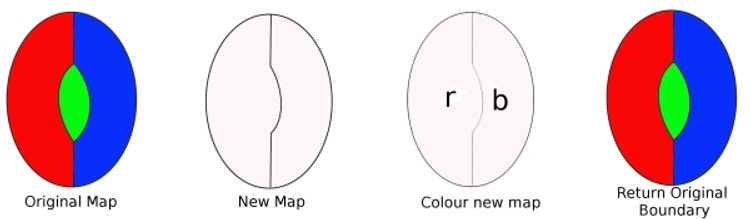
pentru a arăta că un criminal minim nu poate conține o regiune cu două margini (un digon). Să presupunem că existăun criminal minim care conține un digon. Eliminarea unei margini înseamnăharta conține mai puține regiuni. Deci, această nouă hartă poate fi coloratăcu Patru culori. Acum înlocuiți marginea pierdută. Deoarece au fost necesare doar două culori înainte, înlocuirea marginii înseamnă că putem folosi a treia culoare și mai avem încă o a patra culoare de utilizat. Deci, un minimcriminale pot fi colorate cu patru culori. Prin urmare, un minimcriminal nu poate conține un digon.
această procedură poate fi repetată pentru a arăta că un criminal minim nu poate conține o țară cu trei fețe (un trigon), dar se descompune atunci când încercăm tehnica pe un pătrat, deoarece atunci când înlocuim pătratul, țările de lângă acesta pot folosi toate cele patru culori, astfel încât procedura de probă eșuează. Odată ce acest lucru s-a întâmplat, devine evident că nu va funcționa pentru pentagoane și așa mai departe.
Teorema celor șase culori
o tehnică similară poate fi aplicată pentru a arăta că cele șase colourtheorem sunt adevărate. În primul rând, presupunem că nu există hărți care să poatăcolorate cu șase culori. Unele dintre hărți pot fi colorate cu șapte culori, deci selectând una dintre acestea (un criminal minim), dacă putem arăta că este posibil să o colorăm cu mai puțin de șapte culori, ne-am atins scopul.
Din dovada teoremei celor cinci vecini, este posibil să procedăm folosind ideea criminală minimă pentru a arăta că orice hartă poate fi colorată cu șase culori!
de la regiuni la noduri, Rețele și topologie
în 1879 Alfred Kempe (1849-1922), folosind tehnici similare celor descrise mai sus, a pornit de la proprietatea celor cinci vecini și a dezvoltat o procedură cunoscută sub numele de metoda lanțurilor Kempe pentru a găsi o dovadă a teoremei celor patru culori. A publicat această dovadă în Jurnalul American de matematică. El a găsit două versiuni mai simple care au fost publicate în anul următor, iar dovada sa a stat cu zece ani înainte ca Percy Heawood (1861-1955) să arate că există o eroare importantă în metoda de probă pe care Kempe o folosise.


Alfred Kempe (1849-1922), PeterGuthrie Tait (1831-1901) și Percy heawood (1861-1955)
în 1880 P. G. Tait (1831-1901) un fizician matematic, oferito soluție la problemă. În mod independent, Tait stabilise că hărțile în care un număr par de linii de graniță se întâlnesc în fiecare punct,ar putea fi colorate cu două culori, deși acest rezultat a apărut mai devreme în hârtiile lui Kempe.
în perioada 1876-77 Tait a devenit cunoscut pentru studiul său șiclasificarea nodurilor. La acea vreme au existat un număr dediferite teorii despre structura atomilor. William Thompson (mai târziu, Lord Kelvin 1824-1907) inspirat de experimentele fizicianului german Hermann von Helmholtz (1821-1894) a propus ateoria că atomii erau tuburi înnodate de eter. Teoria lui Kelvin despre atomii de cortex a fost luată în serios timp de aproximativ douăzeci de ani și l-a inspirat pe Tait să întreprindă o clasificare a nodurilor. Tait, Thomsonși James Clark Maxwell (1831-1879) au inventat multe idei topologiceîn timpul studiilor lor. Cu toate acestea, teoria lui Kelvin a fost fundamentalăamăgit și fizicienii și-au pierdut interesul pentru munca lui Tait.


Hermann von Helmholtz (1821-1879),Lord Kelvin (1824-1907) și James Clark Maxwell (1831-1879)

Tait a început cu modalitățile prin care o singură buclă închisă de cablu ar putea fi înnodată. El nu a avut nici o metodă sistematică la început și a început într-un mod intuitiv, luând o singură buclă închisă și experimentând modurile în care ar putea fi înnodată. Desigur, cordonul trebuia să fie deschis (ca ashoelace) apoi înnodat și alăturat. Rețineți că, dacă urmați thecord în jurul nodului, trecerile ‘over – under’ vor alterna.Apoi a continuat să experimenteze cu două bucle și modurile în care acestea ar putea fi înnodate împreună. Sunt prezentate aici noduri cu până la șasecrucișări pentru o singură buclă.
unul dintre rezultatele studiului lui Tait a fost conjectura grafului Hamiltonian.
o hartă este privită ca un poliedru desenat pe o sferă și poate fi apoi proiectată pe un plan. Tait a propus ca orice hartă cubică poliedrică să aibă un ciclu Hamiltonian . Metoda lui Tait s-a concentrat pe marginile graficului și a arătat că un ciclu Hamiltonian ar putea produce o hartă cu patru culori. Abia în 1946 William Tutte (1917-2002) a găsitprimul contraexemplu al conjecturii lui Tait.
Tait și legătura cu noduri
Taitinițiat studiul snarks în 1880, când a dovedit că teorema fourcolour a fost echivalent cu afirmația că nu snark isplanar. Un grafic plan este unul care poate fi desenat în plan cufără margini care traversează. Se pare că ideea lui Tait despre grafuri non-plane a venit din studiul său despre noduri și căi Hamiltoniene .
primul snark cunoscut a fost graficul Petersen descoperit în 1898,iar matematicienii au început să vâneze mai multe dintre aceste tipuri de grafuri, dar abia în 1946 a fost găsit un alt snark.
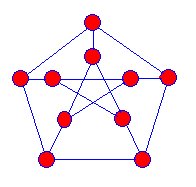 |
SNARKS sunt proiecții de grafice tridimensionale pe theplane. Nu există vârfuri în care marginile albastre par să se încrucișeze. Snarks au următoarele proprietăți:
|
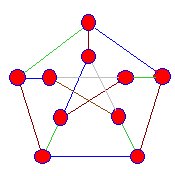 |
marginile care se întâlnesc cu vârfurile acestui snark sunt colorate în albastru,verde și maro, dar ajungem întotdeauna la o etapă în care acest proces nu poate fi continuat. |
Julius Peterson (1839-1910)
the hunting of thesnark este o poezie scrisă de Lewis Carroll, iar Martin gardnernumit aceste grafice SNARKS, pentru că erau atât de evazive.
transformarea problemei și găsirea de noi metode.
deși Heawood a găsit defectul major în metoda de probă a lui Kempe în 1890, el nu a putut continua să demonstreze teorema celor patru culori, dar a făcut o descoperire semnificativă și a dovedit în mod concludent că toate hărțile ar putea fi colorate cu cinci culori.
Heawood a adus multe contribuții importante la problemă,mutând atenția din zonele unei hărți, către granițele dintre ele. Până în 1898 el dovedise că, dacă numărul de margini din jurul fiecărei regiuni este divizibil cu 3, atunci regiunile ar putea fi colorate cu patru culori.
dovada lui Cauchy a formulei lui Euler a inclus, de asemenea, ideea că orice plasă a unui poliedru poate fi triangulată prin adăugarea de margini pentru a face fețe ne-triunghiulare în triunghiuri. Apoi a dezvoltat o procedurăîn care a șters marginile unul câte unul, arătând că forma lui Euler ar putea fi menținută la fiecare pas.
dovada lui Cauchy a formulei lui Euler
dovada lui Cauchy din 1813 a formulei lui Euler a început cu ideea apropierii unui poliedru pentru a obține o plasă plană. El a demonstrat mai departe(a) că orice plasă ar putea fi triangulată, iar dovada sa (b) a formulei lui Euler a fost acceptată la acea vreme.
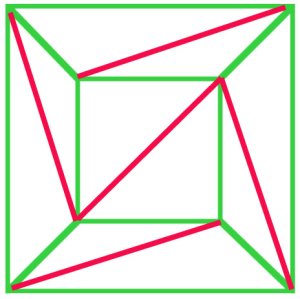 (a)
|
In principle, every polygonal net can be triangulated. In thisnet of a cube (a), $f + v – e$ is $10 + 8 – 17 = 1$, and Euler’sformula still holds. |
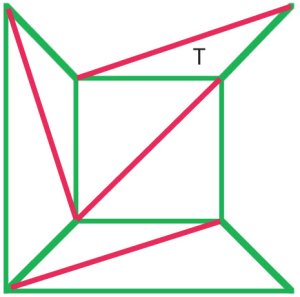 (B)
|
argumentul lui Cauchy a fost de a elimina marginile Externe din diagrama(a) unul câte unul, și când a ajuns la o etapă ca în diagrama (B)A îndepărtat întregul triunghi t, păstrând astfel formula lui Euler. Mulți matematicieni de la începutul secolului al XIX-lea au fost de acord că acest lucruprocedura a demonstrat o dovadă a formulei lui Euler pentru allpolyhedra. |
până în 1900, matematicienii știau că un grafic plan poate ficonstruit din orice hartă folosind conceptul puternic de dualitate . În dual, regiunile sunt reprezentate de vârfuri și două vârfuri sunt unite deo margine dacă regiunile sunt adiacente. În aceste grafice, conjectura FourColour întreabă acum dacă vârfurile grafului pot fi colorate cu 4 culori, astfel încât să nu existe două vârfuri adiacente aceeași culoare.
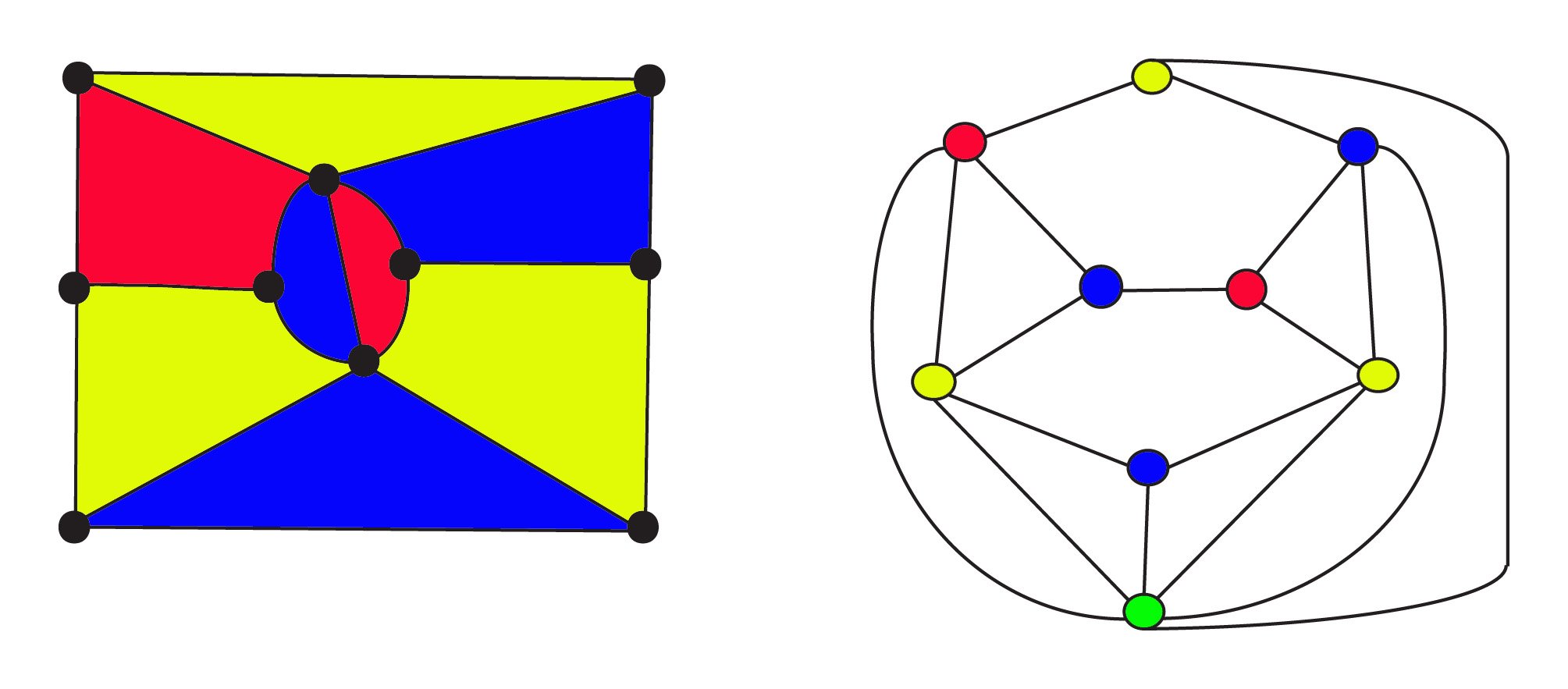
harta cu 3 culori din stânga are 8$regiuni 10 $noduri și 17$ margini. Graficul său dual pe dreapta are regiuni de $9$ 9 $ noduri și margini de $17 $ unde vertexurile sunt colorate la fel ca zonele hărții. Greenvertex din partea de jos a graficului reprezintă infinitul externzona pentru hartă. Atât harta originală, cât și dubla sa respectă Euler ‘ sformula pentru rețele $f + v – E = 1$ sau, $\text{regiuni} +\text{noduri} – \text{margini} = 1$. Relația de dualitate estesimetrică: dualul dualului va fi graficul original, underegiuni și vârfuri sunt schimbate.
în prima jumătate a secolului al XX-lea, matematicienii s-au concentrat pe modificarea acestor tipuri de tehnici pentru a reduce hărțile complicate la cazuri speciale care ar putea fi identificate și clasificate, pentru a investiga proprietățile lor particulare și a dezvoltat ideea unui set minim de configurații de hărți care ar putea fi testate.
în primă instanță, s-a crezut că setul conține aproape 9.000 de membri,ceea ce era o sarcină enormă, așa că matematicienii s-au întors la tehnici computerizate pentru a scrie algoritmi care ar putea face testarea pentru ei. Algoritmii au folosit versiuni modificate ale ideii originale a lanțurilor Kempe împreună cu alte tehnici pentru a reducenumărul de membri ai setului minimal.
după ce a colaborat cu John Koch la problema reductibilității, în 1976 la Universitatea din Illinois, Kenneth Appeland Wolfgang Haken a redus în cele din urmă problema testării la un set anonim cu 1.936 de configurații și a fost realizată o soluție completă la conjectura celor patru culori. Această problemăverificarea reductibilității hărților una câte una a fost dublu verificatăcu diferite programe și computere diferite. Dovada lor a arătat că cel puțin o hartă cu cel mai mic număr posibil de regiuni care necesită cinci culori nu poate exista.
de la prima dovadă, s-au găsit algoritmi mai eficienți pentru hărțile cu 4 culori și, până în 1994, setul inevitabil de configurații a fost redus la 633.
este o ‘dovadă’ făcută pe un Computer o dovadă adecvată?
deoarece dovada a fost făcută cu ajutorul unui computer, a existat un strigăt imediat. Mulți matematicieni și filozofi au susținutcă dovada nu era legitimă. Unii au spus că dovezile ar trebui să fie ‘dovedite’ doar de oameni, nu de mașini, în timp ce alții, cu o minte mai practică, au pus la îndoială fiabilitatea atât a algoritmilor, cât și a capacității mașinilor de a le realiza fără erori.Cu toate acestea, multe dintre dovezile scrise de matematicieni au fostgăsit a fi defect, astfel încât argumentul despre fiabilitate pare gol.Oricare ar fi Opiniile exprimate, situația a produs o discuție serioasă despre natura dovezii care continuă și astăzi.
pentru note pedagogice:
utilizați fila Note din partea de sus a acestui articol sau faceți clic aici .
Note
- Mai multe detalii despre aceasta și celelalte proceduri găsite în această secțiune pot fi văzute în Cartea lui Robin Wilson Patru culori suficiente .
- nodurile pot fi stângaci sau dreptaci, iar astăzi existăaplicații importante ale acestei proprietăți în chimie, farmacie,biologie și fizică. (Vezi notele Pedagogice)
- numit după William Rowan Hamilton (1805-1865). O cale hamiltoniană într-un grafic viziteazăfiecare vârf exact o dată. Un ciclu Hamiltonian (sau circuit) este apath care vizitează fiecare vârf exact o dată și se întoarce la vârful de pornire.(Vezi note Pedagogice)
- cartea lui Imre Lakatos, dovezi și respingeri are o discuție și o critică a procedurii lui Cauchy (paginile 6 – 12) și mult mai multe despre povestea teoremei lui Euler.
- ideea dualității a apărut în secolele 16 și 17 cuevoluții în geometria proiectivă. Matematicieni ca Pascal andDesargues a constatat că noi teoreme ar putea fi găsite prin schimbul theterms ‘punct’ și ‘linie’ în descrieri ale anumitor geometricconfigurations. Un exemplu este în poliedre obișnuite, undevertexurile unuia corespund fețelor celuilalt. Deci dualul unui tetraedru este un alt tetraedru, iar dualul unui cub este un octaedru. Dualul dualului este originalulpoliedru.
cea mai populară și ușor de citit carte despre cele patru ColourTheorem este:
Wilson, R. (2003)
Patru culori sunt suficiente.
Londra. Penguin Books.
pentru o istorie mai detaliată și tehnică, cartea de referință standard este:
Biggs, N.; Lloyd, E.& Wilson, R. (1986) (1998)
Teoria grafurilor,1736-1936
Oxford. Oxford University Press.
aceasta ne aduce la zi, cu fundamente și filozofii mai recente.
Fritsch, R și Fritsch, G (2000)
Teorema celor Patru culori: Istorie,fundații topologice și ideea de dovadă
New York. Springer-Verlag.
aproape nicio carte de istorie generală nu are prea multe despre acest subiect, dar ultimul capitol din Katz numit ‘calculatoare și aplicații’ are o secțiune despre teoria grafurilor, iar Teorema celor patru culori este menționată de două ori.
Polya G. Cum să Rezolvit.
aceasta este cartea clasica despre rezolvarea problemelor. Au existat multe ediții ale acestei cărți de când a apărut pentru prima dată în anii 1950 și este încă ușor disponibilă. În mod curios, edițiile recente au primit subtitlul ‘A new aspect of Mathematical Method’.Lakatos, I. (1976) dovezi șirefutări: logica descoperirii matematice.
Cambridge. C. U. P.
aceasta este o altă carte importantă care a condus la cercetarea în rezolvarea problemelor și investigații în anii 1970. Începe ca o discuție de clasă între un profesor și un grup de studenți despre dovada formulei lui Euler și variază prin ideile, obiecțiile și posibilitățile care au fost de fapt discutate de matematicieni și oameni de știință în secolul al XIX-lea. Se ridică unele dintre cele mai importante probleme cu privire la predarea și rezolvarea problemelor de învățare și despre metode matematice și dovezi.
referințe înrudite
am avut o mică carte despre jocurile cu coarde de ceva timp. Când eram la școală, se numea leagănul pisicii și l-am jucat în timpul nostrutimp de pauză.
recent, un jurnal francez a publicat o lucrare despre’ algebra ‘ figurilor de coarde! Dacă mergeți la Amazon, veți găsi o carte frumoasă de Ann Swain și Michael Taylor numită finger Strings: A Book Of Cats leagane Andstring Figures care va fi publicată de Floris books în Septembrie2008. Există aproximativ 80 de figuri descrise cu culori diagrams.It spirala este legată, așa că va rămâne deschisă în timp ce urmați instrucțiunile. De asemenea, vine cu o pereche de bucle șir!
pentru experții în noduri, AshleyBook of Knots este un clasic pentru oricine este interesat desute de diferite tipuri de noduri și utilizările lor. Amazon arediverse ediții disponibile la prețuri diferite.
link-uri Web
pentru o privire de ansamblu generală și link-uri către mai multe persoane și subiecte, site-ul theMacTutor este
și, desigur, biografiile MacTutor ale celor implicați în dezvoltarea tuturor diferitelor aspecte matematice pot fi găsite la indexul MacTutor Biographies.
Teorema celor patru culori și trei dovezi. Pentru mathematicallypersistent următorul site web are o nouă abordare intrigantă pentru a aborda problema construirii unui nou algoritm pentru rezolvarea problemei și legarea pentru a reduce dependența de un computer.http://www.emu.edu.tr/~cahit/the%20four%20color%20theorem%20—%20three%20proofs.htm
Pentru teoria grafurilor, Wikipedia oferă o imagine de ansamblu bună și putețiskip lucrurile cu adevărat tehnice. Acesta arată tipurile de moderneaplicații ale acestui domeniu al matematicii. Dacă mergeți la GraphColouring și faceți clic pe teorema celor Patru culori, atunci veți găsio mulțime mai multe informații.
o istorie interesantă și nu prea tehnică a teoriei nodurilor-cum o idee din fizica lui Kelvin revine la teoria Atomicăastăzi.
Asociația Profesorilor de matematică au Celtic knotdesign postere. Accesați site-ul lor web și răsfoiți alfabetullista de resurse.
afla totul despre noduri pe Atlas nod! Dacă nu sunteți expert – bucurați-vă doar de varietatea și complexitatea bazei de date „in spirit of wiki”
mai artistic și mai colorat-dar nu mai puțin matematic este site-ul complotului knot.
pentru cei care doresc o parte din lucrurile originale și istoricedetaliu du-te la istoria teoriei nod pe: