Twierdzenie o czterech kolorach
twierdzenie o czterech kolorach zostało po raz pierwszy sformułowane nieco ponad 150 lat temu, a ostatecznie udowodnione ostatecznie w 1976 roku. Jest to wybitny przykład tego, jak stare pomysły łączą się z nowymi odkryciami i technologiami w różnych dziedzinach matematyki, aby zapewnić nowe podejście do problemu. Jest to również przykład, jak pozornie prosty problem uważano za „rozwiązany”, ale potem stał się bardziej złożony, i jest to pierwszy spektakularny przykład, w którym komputer był zaangażowany w udowodnienie twierdzenia matematycznego.
na początku
przypuszczenie, że każda mapa może zostać zabarwiona przy użyciu tylko czterech kolorów, pojawiło się po raz pierwszy w liście od Augusta De Morgana (1806-1871), pierwszego profesora matematyki w new University College London, do jego przyjaciela Williama Rowanhamiltona (1805-1865), słynnego irlandzkiego matematyka w 1852 roku. Zostało zaproponowane de Morganowi przez jednego z jego uczniów, FrederikGuthrie, w imieniu jego starszego brata Francisa (który później został profesorem matematyki na Uniwersytecie w Kapsztadzie).


Augustus De Morgan (1807-1871) andWilliam Rowan Hamilton (1805-1865)
problem, tak po prostu opisany, ale tak kusząco trudno udowodnić, złapał wyobraźnię wielu matematyków w tym czasie. Pod koniec lat 60. De Morgan zabrał nawet problem i swoją pracę do Ameryki, gdzie zainteresował się nim m.in. Benjamin Peirce (1809-1880), znany matematyk i astronom, jako daleko rozwijający swoje metody logiczne.
De Morgan wykorzystał fakt, że na mapie z czterema regionami, każdy z trzech pozostałych, jeden z nich jest całkowicie zamknięty przez pozostałe. Ponieważ nie mógł znaleźć sposobu na udowodnienie tego, użył go jako aksjomatu, podstawy tego dowodu.
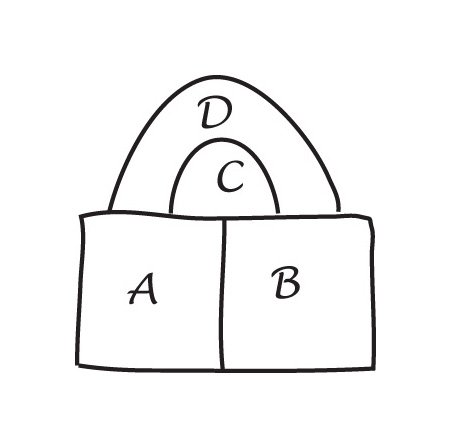
kopia oryginału De Morgana w liście do Hamiltona i prosta czterokolorowa Mapa.
w 1878 roku Arthur Cayley (1821-1895) na spotkaniu Londyńskiego Towarzystwa Matematycznego zapytał, czy ktoś znalazł rozwiązanie dla pierwotnego pytania Morgana, ale mimo pewnych zainteresowań, nikt nie poczynił znaczących postępów. Cayley zainteresował się tym problemem i w 1879 roku opublikował krótki artykuł o kolorowaniu map, w którym wyjaśnił niektóre trudności w próbach sprawdzenia i wniósł istotny wkład w sposób, w jaki problem został rozwiązany. Jego pytanie, że ” jeśli dana mapa jest już zabarwiona czterema kolorami, a dodamy kolejny obszar, to czy możemy zachować tę samą kolorystykę?”rozpoczęła się kolejna linia pytań, która doprowadziła do zastosowania matematycznego ograniczenia problemu.

Arthur Cayley (1821-1895)
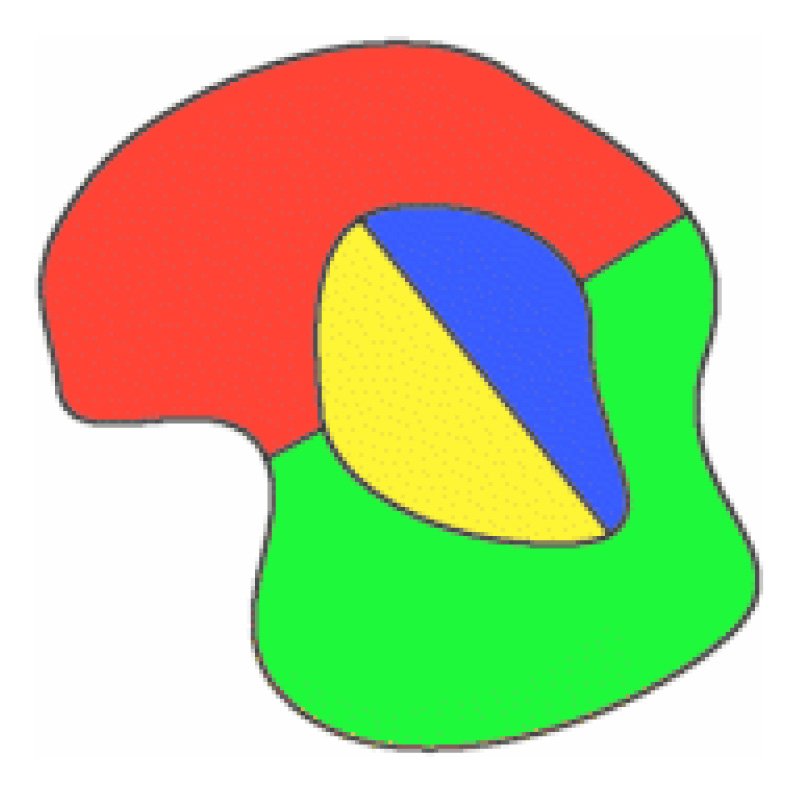
Arthur Cayley pokazał, że jeśli fourcolours został już użyty do pokolorowania mapy, a nowy region został dodany, nie zawsze było możliwe zachowanie oryginalnego kolorowania.
powyżej, wszystkie cztery kolory zostały użyte na oryginalnej mapie, a nowy region jest narysowany, aby go otoczyć. W tym przypadku czerwony region jest zmieniany na niebieski, dzięki czemu czerwony może być używany na nowym regionie otaczającym.
Cayley zauważył również, że możliwe jest rozwiązanie wersji problemu poprzez ograniczenie sposobu, w jaki spełnione są granice. Na przykład mapy, na których spotkały się tylko trzy kraje, mają trzy krawędzie spotykające się w avertex. Są one nazywane „mapami sześciennymi”, a Mapy użyte w dalszej dyskusji są mapami sześciennymi. Ponadto, jeśli mapa może mieć cztery kolory, na mapie pojawią się tylko trzy kolory.
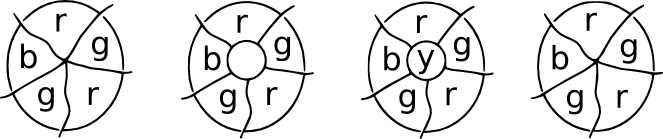
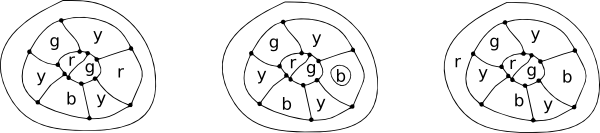
prezentacja patcha. Wyobraź sobie, że w pewnym miejscu na mapie wiele krajów spotyka się w jednym punkcie. Teraz umieść łatkę nad miejscem spotkania, a wszystkie nowe punkty spotkania będą miały trzy granice emanujące z nich. Są to Mapy sześcienne, a czwarty kolor może być użyty dla regionu centralnego. Po usunięciu plastra możemy powrócić do oryginalnej kolorystyki.
kilka starych technik, nowe warunki i więcej problemów!
aby śledzić rozwój problemu, musimy pokrótce zbadać niektóre pomysły, procedury i techniki, które matematycy opracowali w swoich próbach jego rozwiązania.
tylko pięciu sąsiadów Domysli
” Jeśli nie potrafisz rozwiązać problemu, znajdź łatwiejszy, który możesz rozwiązać.”(Polya.
'Każda mapa ma co najmniej jeden kraj z pięcioma lub mniej sąsiadami.”
wyobraź sobie mapę Wyspy otoczonej morzem. Wpoliczaniu krajów Wyspy morze liczymy jako jedenregion. Niektóre kraje mogą mieć tylko dwie granice (digon), niektóre trzy (jak w trójkącie), niektóre cztery (kwadrat) i niektóre pięć (apentagon) lub więcej.
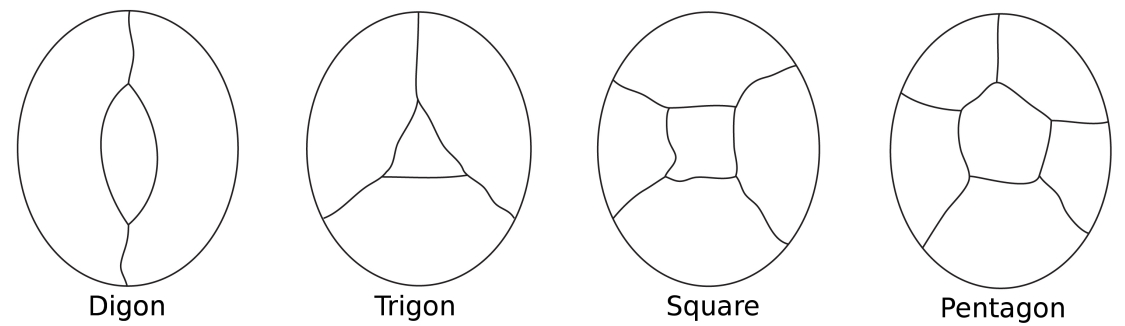
najprostsze możliwe konfiguracje dla otaczającego regionu centralnego.
zauważ, że we wszystkich tych konfiguracjach każdy węzeł ma tylko trzy.
w 1813 r.wzór Eulera na polihedrę został zaadaptowany na dwa wymiary przez Augustina Cauchy ’ ego (1759-1857), przenosząc polihedron na płaszczyznę, tworząc w ten sposób siatkę solidu. W ten sposób formuła stała się $f + v-e = 1$, ponieważ nie liczono „zewnętrznego” obszaru sieci.

Augustin Cauchy (1759-1857)
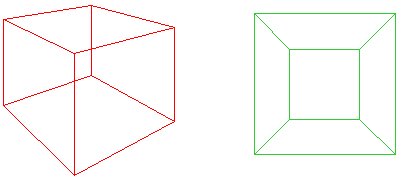
wyobraź sobie zgniatanie czerwonej kostki w dół płaszczyzny tak, aby jej podstawa została otwarta, tworząc zewnętrzną część zielonej siatki. Pomysł Cauchy ’ ego polegał na wycięciu jednej powierzchni wielokąta, tak aby dla wielokąta płaszczyznowego $f + v – e = 1$. Alternatywnie,jeśli „zewnętrzna” siatka jest traktowana jako twarz z nieskończonością, to nadal mamy $f + v – E = 2$
możemy założyć, że istnieją co najmniej trzy linie graniczne (krawędzie)wyłaniające się z każdego punktu spotkania (wierzchołków).
dowód, że na mapie znajduje się co najmniej jeden kraj otoczony pięcioma lub mniej sąsiadami, jest sprzeczny. Jeśli to prowadzi do absurdu, mamy dowód.
Teraz umieść te wartości we wzorze Eulera: $ $ f + v-E = 2$$ i mamy $$1/3(e) + 2/3(e) – E$$ co jest zerem!
To jest absurd, więc nasze pierwotne założenie było fałszywe.Oznacza to, że musi istnieć co najmniej jeden kraj z pięcioma lub mniej sąsiadami!
Minimal Criminals!
innym sposobem na rozwiązanie problemu czterech kolorów jest założenie, że jest on odpowiedni i zobacz do czego to prowadzi. Załóżmy, że istnieją mapy, które wymagają pięciu kolorów lub więcej, a my wybieramy mapy z najmniejszą możliwą liczbą krajów. Mapy te nazywane są minimalnymi kontrprzykładami lub minimalnymi przestępcami !
oznacza to,że minimal criminal nie może być pokolorowany czterema kolorami, ale każda mapa z mniejszą liczbą krajów może być pokolorowana czterema kolorami. Jeśli pokażemy, że minimalni przestępcy nie mogą istnieć, może uda nam się zrobić jakiś postęp.
na przykład, możemy pokazać, że minimalny przestępca nie może zawierać digonu.
z oryginalnej mapy wyjmij granicę z digonu, a otrzymasz nową mapę z mniejszą liczbą krajów. Mapa ta może być kolorowana na cztery kolory (z naszego założenia). Następnie kolorujemy tę nową mapę (potrzebujemy tylko dwóch kolorów). Teraz wymień obramowanie, które usunęliśmy,i pokoloruj mapę. Użyliśmy trzech kolorów, a ponieważ dostępny jest jeszcze jeden kolor, pokazuje to, że nasza mapa może zostać zabarwiona czterema kolorami. Ale to wbrew naszym założeniom, więc minimalny przestępca nie może zdobyć digona.
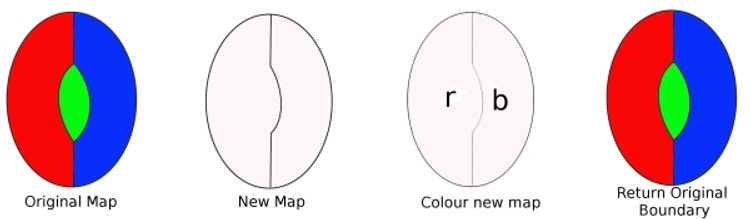
Przypuśćmy, że istnieje minimalny przestępca, który zawiera digona. Usunięcie krawędzi oznacza, że mapa zawiera mniej regionów. Więc ta nowa mapa może być kolorowana na cztery kolory. Teraz wymień utraconą krawędź. Ponieważ wcześniej potrzebne były tylko dwa kolory, wymiana krawędzi oznacza, że możemy użyć trzeciego koloru, a nadal mamy czwarty kolor do użycia. Tak więc minimalcriminal może być zabarwiony czterema kolorami. Stąd minimalcriminal nie może zawierać digona.
tę procedurę można powtórzyć, aby pokazać, że minimalna kara nie zawiera trójstronnego kraju (trygonu), ale rozkłada się, gdy spróbujemy tej techniki na kwadracie, ponieważ gdy zastąpimy kwadrat, kraje znajdujące się obok mogą używać wszystkich czterech kolorów, więc procedura dowodowa nie powiedzie się. Kiedy to się stanie, staje się oczywiste, że to nie zadziała dla pentagonów i tak dalej.
twierdzenie o sześciu kolorach
podobną technikę można zastosować, aby pokazać, że sześć kolorów jest prawdą. Po pierwsze, Zakładamy, że nie ma map, które mogą być zabarwione sześcioma kolorami. Niektóre mapy mogą być wybarwione siedmioma kolorami, więc wybierając jedną z nich (minimalistyczny przestępca), jeśli możemy pokazać, że można ją pokolorować mniej niż siedmioma kolorami, osiągnęliśmy nasz cel.
z dowodu twierdzenia pięciu sąsiadów wynika, że można użyć minimalistycznego pomysłu kryminalnego, aby pokazać, że każda mapa może być pokolorowana sześciokolorami!
od regionów do węzłów, sieci i topologii
w 1879 r.Alfred Kempe (1849-1922), używając technik podobnych do opisanych powyżej, rozpoczął od „własności pięciu sąsiadów” i opracował procedurę znaną jako metoda „łańcuchów Kempe”, aby znaleźć dowód twierdzenia czterech kolorów. Opublikował ten dowód w American Journal of Mathematics. Znalazł dwie prostsze wersje, które zostały opublikowane w następnym roku, a jego dowód trwał dziesięć lat, zanim Percy Heawood (1861-1955) wykazał, że istnieje istotny błąd w metodzie proof, której użył Kempe.


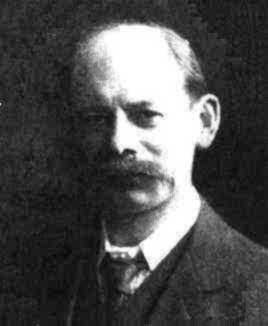
Alfred Kempe (1849-1922), PeterGuthrie Tait (1831-1901) i Percy heawood (1861-1955)
w 1880 P. G. Tait (1831-1901) fizyk matematyczny, zaproponował rozwiązanie tego problemu. Niezależnie Tait ustalił,że mapy, w których parzysta liczba linii granicznych spotyka się w każdym punkcie, mogą być barwione dwoma kolorami, chociaż taki wynik pojawił się wcześniej w dokumentach Kempe.
w latach 1876-77 Tait stał się znany ze swoich badań i klasyfikacji węzłów. W tym czasie było wiele różnych teorii na temat struktury atomów. William Thompson (późniejszy Lord Kelvin 1824-1907) zainspirowany eksperymentami niemieckiego fizyka Hermanna von Helmholtza (1821-1894) zaproponował, że atomy są wiązanymi rurkami eteru. Teoria Kelvina o 'atomach Vortex’ była traktowana poważnie przez około dwadzieścia lat i zainspirowała Tait do przeprowadzenia klasyfikacji węzłów. Tait, Thomson i James Clark Maxwell (1831-1879) w trakcie swoich badań wymyślili wiele ideologii topologicznych. Teoria Kelvina była jednak Fundamentalna i fizycy stracili zainteresowanie pracą Taita.


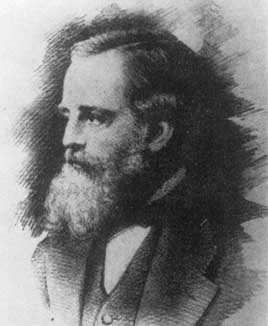
Hermann von Helmholtz (1821-1879),Lord Kelvin (1824-1907) i James Clark Maxwell (1831-1879)

Tait rozpoczął się od sposobów, wktórych można wiązać pojedynczą zamkniętą pętlę Sznurka. Na początku nie miał metody systematycznej, a zaczynał w intuicyjny sposób, przyjmując pojedynczą zamkniętą pętlę i eksperymentując ze sposobami, w jakie można ją wiązać. Oczywiście sznur musiał być otwarty (jak ashoelace), a następnie wiązany i łączony. Zauważ, że jeśli podążasz za liną wokół węzła, przejścia „over-under”będą się zmieniać.Następnie eksperymentował z dwiema pętlami i sposobami ich łączenia. Pokazano tutaj węzły z maksymalnie sześcioma krzyżami dla Pojedynczej Pętli.
jednym z wyników badań Taita były hipotezy grafów Hamiltońskich.
Mapa jest traktowana jako wielościan narysowany na kuli i może być rzutowana na płaszczyznę. Tait zaproponował, że każda mapa kubicpolyhedralna ma Hamiltoniancykl . Metoda Taita skupiła się na krawędziach grafu i wykazała, że cykl Hamiltoński może wytworzyć czterokolorową mapę. Dopiero w 1946 roku William Tutte (1917-2002) znalazł pierwszy kontrprzykład do domysłów Taita.
Tait i związek z węzłami
Tait zapoczątkowali badania snarków w 1880 roku, kiedy udowodnił, że twierdzenie fourcoloura jest równoważne twierdzeniu, że żaden snark nie jest planistą. Graf planarny to taki, który można narysować na płaszczyźnie bez przecinających się krawędzi. Wygląda na to, że pomysł Taita o grafomierze nieplanarnej pochodzi z jego badań węzłów i ścieżek Hamiltonowych .
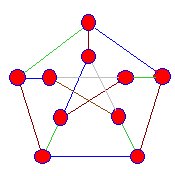
pierwszym znanym snarkiem był Wykres Petersena odkryty w 1898 roku,a matematycy zaczęli polować na więcej tego rodzaju grafów, ale dopiero w 1946 roku znaleziono kolejny snark.
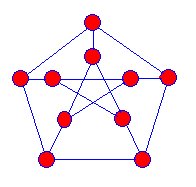 |
snarki to projekcje trójwymiarowych wykresów na planszy. Nie ma wierzchołków, w których niebieskie krawędzie wydają się przecinać inne. Snarki mają następujące właściwości:
|
krawędzie stykające się z wierzchołkami tego warkocza są koloru niebieskiego,zielonego i brązowego, ale zawsze osiągamy etap, w którym ten proces nie może być kontynuowany. |

Julius Peterson (1839-1910)
Polowanie of thesnark to wiersz napisany przez Lewisa Carrolla, a Martin gardnernazwał te wykresy snarkami, ponieważ były one tak nieuchwytne.
przekształcenie problemu i znalezienie nowych metod.
chociaż Hewood znalazł główną wadę w metodzie proof Kempe ’ a w 1890 roku, nie był w stanie udowodnić twierdzenia o czterech kolorach, ale dokonał znaczącego przełomu i udowodnił, że wszystkie mapy mogą być kolorowe z pięcioma kolorami.
Heawood wniósł wiele ważnych rzeczy do problemu,przenosząc skupienie uwagi z obszarów mapy na granice między nimi. Do 1898 roku udowodnił, że jeśli liczba obwodów wokół każdego regionu jest podzielna przez 3, to regiony mogą być zabarwione czterema kolorami.
dowód Cauchy ’ ego ze wzoru Eulera zawierał również ideę, że sieć wielościanu może być trójkątowana przez dodanie krawędzi do powierzchni makenona-trójkąta w trójkąty. Następnie opracował procedurę, w której usuwał krawędzie jeden po drugim, pokazując, że formula Eulera może być utrzymywana na każdym kroku.
dowód Cauchy 'ego na wzór Eulera
dowód Cauchy’ ego na wzór Eulera z 1813 roku rozpoczął się od pomysłu aprojekcji wielościanu w celu uzyskania siatki płaskiej. Ponadto stwierdził (a), że każda siatka może być triangulowana, a jego dowód(b) wzoru Eulera został zaakceptowany w tym czasie.
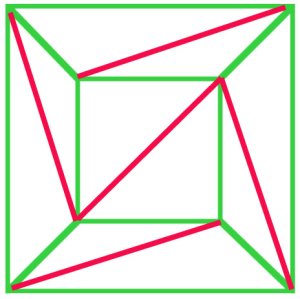 (a)
|
In principle, every polygonal net can be triangulated. In thisnet of a cube (a), $f + v – e$ is $10 + 8 – 17 = 1$, and Euler’sformula still holds. |
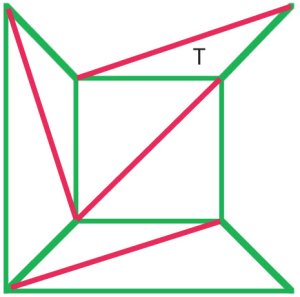
argumentem Cauchy ’ ego było usunięcie zewnętrznych krawędzi z diagramu(a) jeden po drugim, a gdy osiągnął etap jak na diagramie b)usunięto cały trójkąt t, zachowując w ten sposób wzór Eulera. Wielu matematykăłw z poczÄ … tku XIX wieku zgodziĹ 'o siÄ™, Ĺźe proces ten wykazaĺ’ dowĂłd formuły Eulera dla allpolyhedry. |
do 1900 roku matematycy wiedzieli, że wykres planarny może zostać skonstruowany z dowolnej mapy za pomocą potężnego pojęcia dualności . W układzie dualnym są reprezentowane przez wierzchołki, a dwa wierzchołki są połączone krawędzią, jeśli regiony są sąsiadujące. Na tych wykresach domysł FourColour pyta teraz, czy wierzchołki wykresu mogą zostać zabarwione 4 kolorami, tak aby żadne dwa sąsiadujące wierzchołki nie były tym samym kolorem.
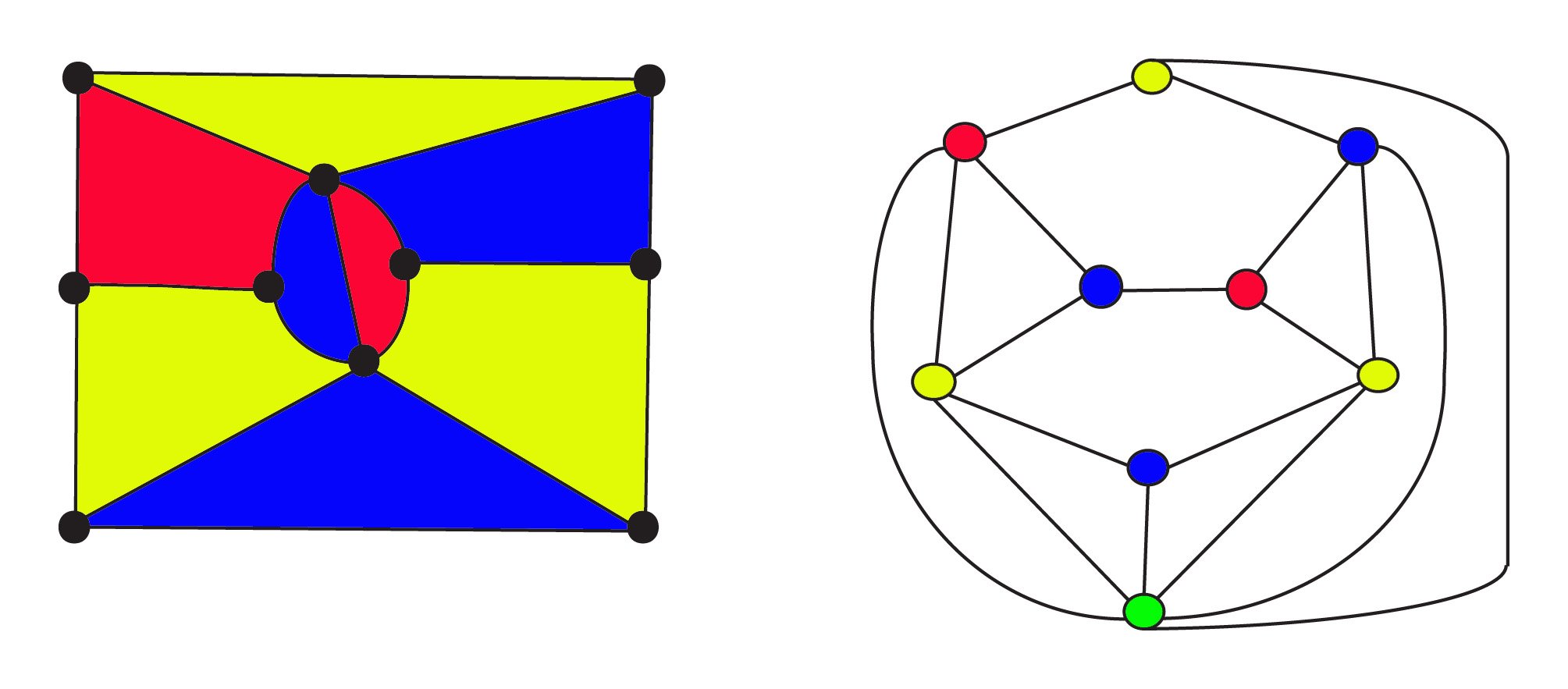
3-kolorowa Mapa po lewej stronie ma$8$ regiony $10$ wierzchołki i $17$ krawędzie. Jej podwójny Graf na mapie ma $ 9 $ regiony $ 9 $ wierzchołki i $ 17 $ krawędzie, gdzie wierzchołki są zabarwione tak samo jak obszary mapy. Greenvertex na dole wykresu reprezentuje nieskończoną zewnętrzną powierzchnię mapy. Zarówno oryginalna mapa, jak i jej podwójny układ są zgodne z formułą Eulera dla sieci $f + v – E = 1$ lub, $\text{regiony} +\text{wierzchołki} – \text{krawędzie} = 1$. Relacja dualności jest symetryczna: dualizm z dualności będzie pierwotnym wykresem, gdzie wymieniane są wierzchołki i wierzchołki.
w pierwszej połowie XX wieku matematycy skupili się na modyfikowaniu tego rodzaju technik w celu zredukowania skomplikowanych map do szczególnych przypadków, które można by zidentyfikować i sklasyfikować, aby zbadać ich szczególne właściwości i rozwinąć ideę minimalnego zestawu konfiguracji map, które można by przetestować.
w pierwszej kolejności uważano, że zbiór zawiera blisko 9 000 członków,co było ogromnym zadaniem, dlatego matematycy zwrócili się do technik komputerowych o napisanie algorytmów, które mogłyby zrobić dla nich test. Algorytmy wykorzystywały zmodyfikowane wersje oryginalnej idei łańcuchów Kempe ’ a wraz z innymi technikami w celu zmniejszenia liczby członków zestawu minimalnego.
Po współpracy z Johnem Kochem nad problememredukowalności, w 1976 roku na Uniwersytecie Illinois Kenneth Appeland Wolfgang Haken ostatecznie zredukował problem testowania do zestawu unikalnego z 1936 konfiguracjami i osiągnięto kompletne rozwiązanie dla domysłów czterech kolorów. Ten problem kontroli redukowalności map jeden po drugim był dwukrotnie sprawdzany za pomocą różnych programów i różnych komputerów. Ich dowód wykazał, że nie może istnieć co najmniej jedna mapa z najmniejszą możliwą liczbą regionów wymagających pięciu kolorów.
od czasu pierwszego dowodu znaleziono bardziej wydajne algorytmy dla map 4-kolorowych, a do 1994 roku nieunikniony zbiór konfiguracji został zredukowany do 633.
czy „dowód” zrobiony na komputerze jest właściwym dowodem?
ponieważ dowód został wykonany przy pomocy komputera, nie było natychmiastowe oburzenie. Wielu matematyków i filozofów twierdziło, że dowód nie był uzasadniony. Niektórzy twierdzili, że dowody powinny być „udowodnione” przez ludzi, a nie Maszyny, podczas gdy inni o bardziej praktycznym umyśle kwestionowali wiarygodność zarówno algorytmów, jak i zdolność maszyn do ich przeprowadzenia bez błędu.Jednak wiele z dowodów napisanych przez matematyków okazało się błędnych, więc argument o wiarygodności wydaje się pusty.Niezależnie od wyrażanych opinii, sytuacja wywołała poważną dyskusję na temat natury dowodu, która nadal trwa.
notatki pedagogiczne:
użyj zakładki notatki na górze tego artykułu lub kliknij tutaj .
uwagi
- więcej szczegółów na ten temat i inne procedury znajdujące się w tej sekcji można zobaczyć w książce Robina Wilsona Four Colours Enough .
- węzły mogą być leworęczne lub praworęczne, a dziś istnieją ważne zastosowania tej właściwości w chemii,farmacji, Biologii i fizyce.
- nazwany na cześć Williama Rowana Hamiltona (1805-1865). Hamiltonian ścieżka w grafie odwiedza każdy wierzchołek dokładnie raz. Cykl Hamiltonowy (lub Obwód) to apath, który odwiedza każdy wierzchołek dokładnie raz i powraca do początkowego wierzchołka.
- książka Imre Lakatosa „dowody i obalenia” zawiera refleksję i krytykę procedury Cauchy ’ ego (strony 6 – 12), a także bardziej historię twierdzenia Eulera.
- idea dwoistości powstała w XVI i XVII wieku wraz z rozwojem geometrii rzutowej. Matematycy tacy jak Pascal i Desargues odkryli, że nowe twierdzenia można znaleźć, wymieniając „punkt” i „linię” w opisach pewnych konfiguracji geometrycznych. Przykładem jest regularna polihedra, gdzienartykuły jednego odpowiadają powierzchniom drugiego. Zatem Dual czworościanu jest kolejnym czworościanem, a dual sześcianu jest ośmiościanem. Dual z dual jest oryginalnympolyhedron.
najbardziej popularna, czytelna książka o czterech kolorach to:
Wilson, R. (2003)
Cztery kolory wystarczają.
Londyn. Penguin Books.
dla bardziej szczegółowej i technicznej historii, standardowa książka jest:
Biggs, N.; Lloyd, E.& Wilson, R. (1986) (1998)
Graph Theory,1736-1936
Oxford. Oxford University Press.
Ten przybliża nas na bieżąco, z nowszymi podstawami i filozofią.
Fritsch, R and Fritsch, G (2000)
The Four Color Theorem: History,Topological Foundations, and Idea of Proof
New York. Springer-Verlag.
prawie żadna książka o historii ogólnej nie ma wiele na ten temat, ale ostatni rozdział w Katz zatytułowany „Komputery i aplikacje” ma sekcję na temat teorii grafów, a twierdzenie o czterech kolorach jest wspomniane.
Polya G. Jak rozwiązać problem.
to klasyczna książka o rozwiązywaniu problemów. Było wiele wydań tej książki, ponieważ pojawiła się po raz pierwszy w latach 50.i nadal jest łatwo dostępna. Co ciekawe, ostatnie wydania zyskały podtytuł „nowy aspekt metody matematycznej”.
Lakatos, I. (1976). Proofs andRefutations: the Logic of Mathematical Discovery.
Cambridge. C. U. P.
jest to kolejna ważna książka, która doprowadziła do badań nad rozwiązywaniem problemów i dochodzeniami w latach 70. Zaczyna się jako pokojowa dyskusja między nauczycielem a grupą studentów na temat dowodu formuły Eulera, a rozciąga się poprzez idee,zastrzeżenia i możliwości, które były faktycznie omawiane przez matematykówi naukowców w XIX wieku. Porusza najważniejsze zagadnienia dotyczące nauczania i uczenia się, rozwiązywania problemów oraz metod matematycznych i dowodów.
odnośniki
od jakiegoś czasu mam małą książkę o grach strunowych. Kiedy byłem w szkole, nazywała się Kocia kołyska i graliśmy w nią w naszych czasach.
Ostatnio francuski dziennik opublikował artykuł na temat „figur smyczkowych”! Na Amazonce znajdziecie książkę Ann Swain i Michaela Taylora pt. Finger Strings: A Book of Cats Cradles andString Figures, która ukaże się nakładem Floris books we wrześniu 2008 roku. Jest około 80 figurek opisanych kolorowymi diagrams.It ’ s spirala związana, więc pozostanie otwarta, podczas gdy ty postępuj zgodnie z instrukcjami. Jest również wyposażony w kilka pętli strunowych!
dla ekspertów od węzłów, AshleyBook of Knots to klasyka dla każdego, kto interesuje się różnymi rodzajami węzłów i ich zastosowaniami. Amazon maróżne edycje dostępne w różnych cenach.
linki do stron internetowych
aby uzyskać ogólny przegląd i linki do wielu osób i tematów, strona internetowa mactutor jest
i oczywiście biografie MacTutor osób zaangażowanych w rozwijanie wszystkich różnych aspektów matematycznych można znaleźć w indeksie biografii MacTutor.
twierdzenie o czterech kolorach i trzy dowody. Dla matematyków poniższa strona internetowa ma intrygujące nowe podejście do problemu konstruowania nowego algorytmu rozwiązania problemu, a także do ograniczenia polegania na komputerze.http://www.emu.edu.tr/~cahit/the%20four%20color%20theorem%20—%20three%20proofs.htm
Jeśli chodzi o teorię grafów, Wikipedia daje dobry przegląd, a można znaleźć naprawdę techniczne rzeczy. Pokazuje rodzaje współczesnych zastosowań tej dziedziny matematyki. Jeśli przejdziesz do GraphColouring i klikniesz na twierdzenie o czterech kolorach, znajdziesz dużo więcej informacji.
ciekawa i niezbyt techniczna Historia teorii węzłów-jak pomysł z fizyki Kelvina wraca do teorii atomów.
Stowarzyszenie Nauczycieli matematyki ma swoje plakaty. Przejdź do ich strony internetowej i przeglądaj alfabetyczną listę zasobów.
Dowiedz się wszystkiego o węzłach w Atlasie węzłów! Jeśli nie jesteś ekspertem – po prostu ciesz się różnorodnością i złożonością bazy danych „inthe spirit of wiki”
bardziej artystyczna i kolorowa – ale nie mniej matematyczna jest strona fabularna.
dla tych, którzy chcą trochę oryginalnych rzeczy i historii, przejdź do historii teorii węzłów na: