De Vierkleurstelling
het Vierkleurvermoeden werd voor het eerst iets meer dan 150 jaar geleden gesteld, en werd uiteindelijk in 1976 definitief bewezen. Het is een uitstekend voorbeeld van hoe oude ideeën combineren met nieuwe ontdekkingen en technieken op verschillende gebieden van de wiskunde om nieuwe benaderingen van een probleem te bieden. Het is ook een voorbeeld van hoe men dacht dat een ogenschijnlijk eenvoudig probleem ‘opgelost’ was, maar toen complexer werd, en het is het eerste spectaculaire voorbeeld waar een computer betrokken was bij het bewijzen van een wiskundige stelling.
In het begin
het vermoeden dat een kaart met slechts vier kleuren kon worden gekleurd, verscheen voor het eerst in een brief vanaugustus De Morgan (1806-1871), eerste hoogleraar wiskunde aan het new University College London, aan zijn vriend William RowanHamilton (1805-1865), de beroemde Ierse wiskundige in 1852. Het was de Morgan voorgesteld door een van zijn studenten, FrederikGuthrie, namens zijn oudere broer Francis (die later professor in de wiskunde werd aan de Universiteit van Kaapstad).


Augustus De Morgan (1807-1871) en William Rowan Hamilton (1805-1865)
het probleem, zo eenvoudig beschreven, maar zo tantalizingly difficultto prove verbeelding van vele wiskundigen in die tijd. In de late jaren 1860 nam de Morgan het probleem en zijnproof zelfs mee naar Amerika, waar onder andere Benjamin Peirce (1809-1880), een tamme wiskundige en astronoom, geïnteresseerd raakte in het als weg om zijn logische methoden te ontwikkelen.
De Morgan gebruikte het feit dat op een kaart met vier regio ‘ s, elk met de andere drie, één van hen volledig omsloten is door de andere. Omdat hij geen manier kon vinden om dit te bewijzen, gebruikte hij het als een axioma , de basis van zijn bewijs.
een kopie van de Morgan ‘ s originalsketch in zijn brief aan Hamilton en een eenvoudige vierkleurige kaart.in 1878 vroeg Arthur Cayley (1821-1895) tijdens een bijeenkomst van de LondonMathematical Society of iemand een oplossing had gevonden voor de oorspronkelijke vraag van Morgan, maar hoewel er interesse was geweest, had niemand significante vooruitgang geboekt. Cayley werd geinteresseerd in het probleem en publiceerde in 1879 een korte paper over de kleuring van kaarten, waar hij enkele moeilijkheden uitlegde bij het proberen een proefdruk te krijgen en een aantal belangrijke bijdragen leverde aan de manier waarop het probleem werd aangepakt. Zijn vraag: “als een bepaalde kaart al met succes is gekleurd met vier kleuren, en we voegen een ander gebied toe,kunnen we dan nog steeds dezelfde kleur behouden?”begon een andere onderzoekslijn die leidde tot de toepassing van wiskundeinductie op het probleem.

Arthur Cayley (1821-1895)
Arthur Cayley toonde aan dat als fourcolours had reeds zijn gebruikt om de kleur van een kaart, en een nieuwe regio wasadded, het was niet altijd mogelijk om de originalcolouring.
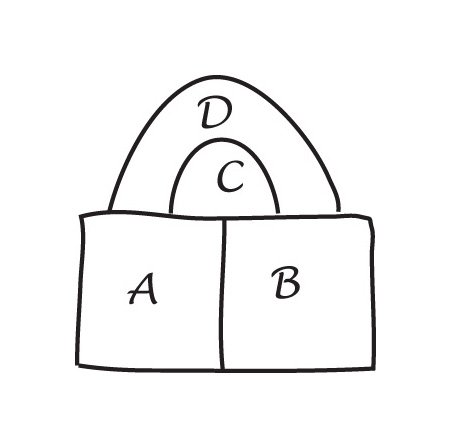
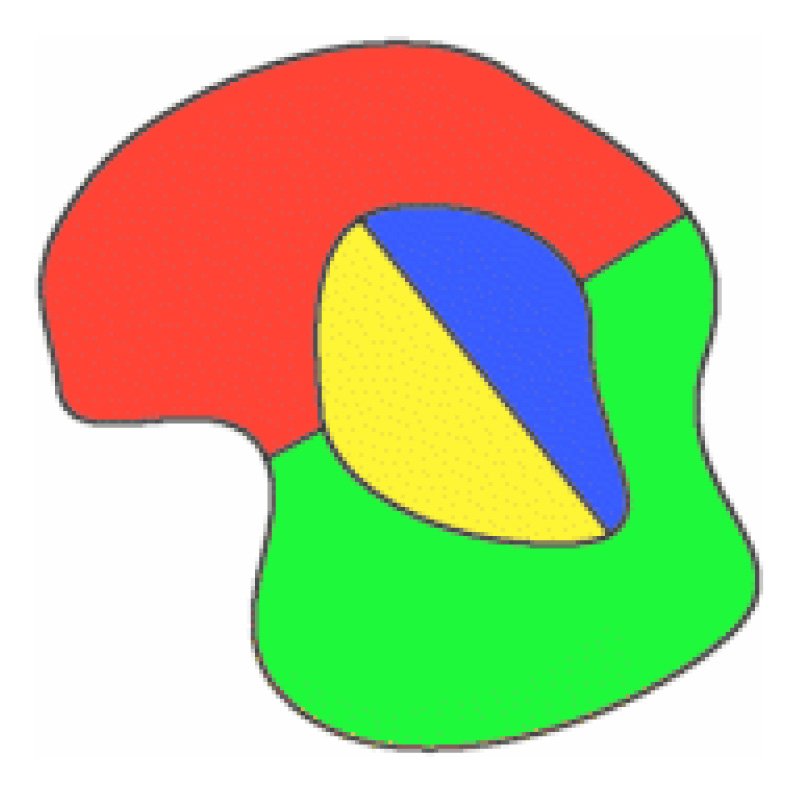
hierboven zijn alle vier de kleuren gebruikt op de oorspronkelijke kaart, en een nieuw gebied wordt getekend om het te omringen. In dit geval is een rode regio veranderd naar blauw, zodat rood kan worden gebruikt op de nieuwe omringende regio.
Cayley merkte ook op dat het mogelijk was een versie van het probleem op te lossen door de manier waarop de grenzen werden bereikt, te beperken. Bijvoorbeeld, kaarten waar slechts drie landen met elkaar hebben drie randen vergadering bij avertex. Deze worden ‘kubieke kaarten’ genoemd, en de kaarten die in de volgende discussie worden gebruikt, zijn allemaal kubieke kaarten. Ook als een kaart met vier kleuren kan worden gekleurd, zullen er slechts drie kleuren op de rand verschijnen.
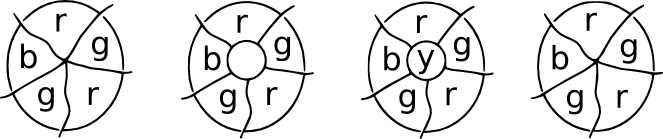
de Patchdemonstratie. Stel je voor dat op een bepaalde plaats op een kaart een aantal landen elkaar op een bepaald punt ontmoeten. Zet nu een patch over het ontmoetingspunt, en alle nieuwe vergaderpunten zullen drie grenzen hebben die van hen uitgaan. Dit zijn kubieke kaarten,en een vierde kleur kan worden gebruikt voor de centrale regio. Na het verwijderen van de patch, kunnen we terugkeren naar de oorspronkelijke kleur.
enkele oude technieken, nieuwe condities en meer problemen!
om de ontwikkelingen van het probleem te volgen, moeten we kort enkele ideeën, procedures en technieken onderzoeken die wiskundigen ontwikkelden in hun pogingen om het op te lossen.
het vermoeden van de enige vijf buren
‘als je een bepaald probleem niet kunt oplossen, vind dan een eenvoudiger probleem dat je kunt oplossen.”(Polya. Hoe het op te lossen)
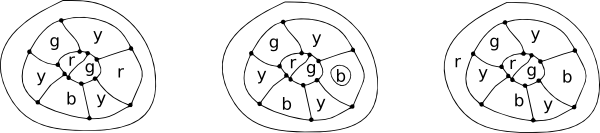
‘elke kaart heeft ten minste één land met vijf of minder buren.’
stel je een kaart voor van een eiland omringd door de zee. In de kleuren van de landen van het eiland, rekenen we de zee als een regio. Sommige landen kunnen slechts twee grenzen hebben (een digon), iets drie (zoals in een driehoek), ongeveer vier (een vierkant) en ongeveer vijf (apentagon) of meer.
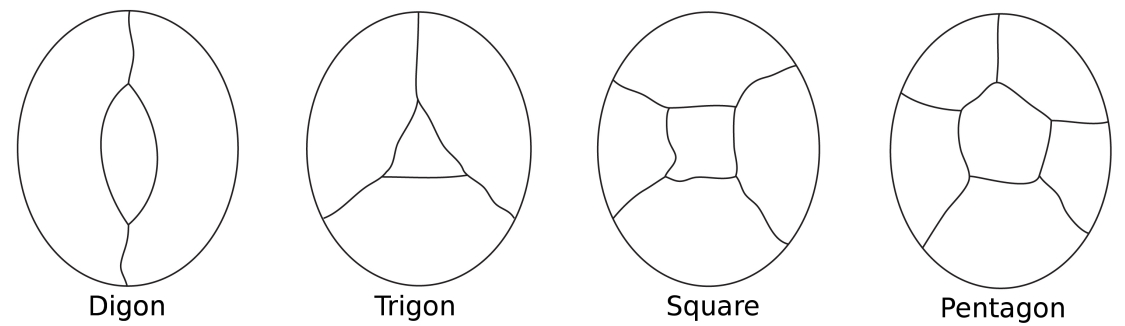
de eenvoudigste mogelijke configuraties voor het omringen van een centraal gebied.
merk op dat in al deze configuraties elk knooppunt slechts driehoeken heeft.
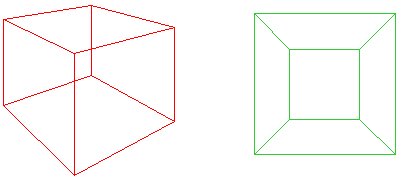
in 1813 werd Eulers formule voor veelvlakken aangepast voor twee dimensies door Augustin Cauchy (1759-1857) door de veelvlakken op een vlak te projecteren en zo het net van thesolid te vormen. Op deze manier werd de formule $f + v – e = 1$, wantecauchy telde niet de ‘buiten’ regio van het net.

Augustin Cauchy (1759-1857)
Stel pletten van de rode kubus downonto een vliegtuig, zodat de basis wordt geopend aan het vormen van de outsideedge van het groene net. Cauchy ‘ s idee was om een gezicht van de buis uit te snijden, zodat voor een vliegtuig veelhoek, $f + v – e = 1$. Als alternatief,als de ‘buitenkant’ van het net wordt beschouwd als een gezicht met infinitearea, dan hebben we nog steeds $f + v – e = 2$
We kunnen aannemen dat er ten minste drie randlijnen (randen)ontstaan uit elk trefpunt (hoekpunten).
het bewijs dat op de kaart ten minste één land is omringd door vijf of minder buurlanden, wordt geleverd door tegenstrijdigheid. Als dit tot een absurditeit leidt, hebben we een bewijs.
plaats nu deze waarden in de formule van Euler: $$f + v-e = 2$$ en we hebben $ $ 1/3(e) + 2/3 (e) – e$$ wat nul is!
Dit is de absurditeit, dus onze oorspronkelijke aanname was onjuist.Dat betekent dat er tenminste één land moet zijn met vijf of minder buurlanden!
minimale criminelen!
een andere manier om het vierkleurenprobleem aan te pakken is aan te nemen dat het fout is, en te zien waar dit toe leidt. Stel dat er kaarten zijn die vijf kleuren of meer nodig hebben, en we kiezen de kaarten met het kleinst mogelijke aantal landen. Deze kaarten worden minimal counter-examples ofminimal criminelen genoemd !
Dit betekent dat een minimale crimineel niet met vier kleuren kan worden gekleurd,maar dat elke kaart met minder landen met vier kleuren kan worden gekleurd. Als we kunnen aantonen dat minimale criminelen niet kunnen bestaan, dan kunnen we misschien wat vooruitgang boeken.
bijvoorbeeld, we kunnen aantonen dat een minimale crimineel geen digon kan bevatten.
van de oorspronkelijke kaart, neem een grens van de digon weg, en we krijgen een nieuwe kaart met minder landen. Deze kaart kan worden ingekleurd met vier kleuren (uit onze aanname). We Kleuren dan deze nieuwe kaart, (we hebben maar twee kleuren nodig). Vervang nu de rand die we hebben verwijderd en kleur de kaart opnieuw. We hebben drie kleuren gebruikt, en aangezien er nog één kleur beschikbaar is, laat dit zien dat onze kaart met vier kleuren kan worden gekleurd. Maar dit is tegen onze veronderstelling,dus een minimale crimineel kan geen digon bevatten.
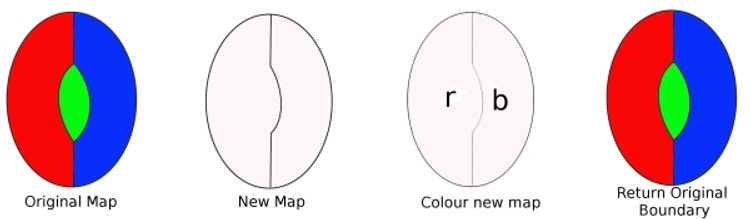
om aan te tonen dat een minimale straf niet een regio met twee randen (een digon) kan bevatten. Stel dat er een minimale crimineel is die een digon bevat. Het verwijderen van een rand betekent dat de kaart minder regio ‘ s bevat. Deze nieuwe kaart kan dus inkleuren met Vier Kleuren. Vervang nu de verloren rand. Omdat er eerder slechts twee kleuren nodig waren, betekent het vervangen van de rand dat we een derde kleur kunnen gebruiken, en nog steeds een vierde kleur hebben om te gebruiken. Een minimalcrimineel kan dus met vier kleuren worden ingekleurd. Een minimalcrimineel kan dus geen digon bevatten.
deze procedure kan worden herhaald om aan te tonen dat een minimale straf niet een driezijdig land (een trigon) kan bevatten, maar het breekt af wanneer we de techniek op een vierkant proberen, want wanneer we het vierkant vervangen, kunnen de landen ernaast alle vierkleuren gebruiken, zodat de bewijsprocedure faalt. Als dit eenmaal gebeurd is, wordt het duidelijk dat het niet zal werken voor vijfhoeken, enzovoort.
de Zeskleurstelling
een soortgelijke techniek kan worden toegepast om aan te tonen dat de zeskleurentheorem waar is. Ten eerste gaan we ervan uit dat er geen kaarten zijn die met zes kleuren kunnen worden gekleurd. Sommige kaarten kunnen worden ingekleurd met zeven kleuren, dus als we een van deze (een minimale crimineel) selecteren, als we kunnen aantonen dat het mogelijk is om deze met minder dan zeven kleuren in te kleuren, hebben we ons doel bereikt.
uit het bewijs van de stelling van de vijf Buren is het mogelijk om het minimale criminele idee te gebruiken om aan te tonen dat elke kaart met zes kleuren kan worden gekleurd!
From Regions to Knots, Networks and Topology
in 1879 startte Alfred Kempe (1849-1922) met technieken die vergelijkbaar zijn met de hierboven beschreven technieken, vanuit de ‘Five neighbours property ‘en ontwikkelde een procedure die bekendstaat als de methode van’ Kempe Chains ‘ om een bewijs van de vier kleurstelling te vinden. Hij publiceerde dit bewijs in het American Journal of Mathematics. Hij vond twee eenvoudigere versies die in het volgende jaar werden gepubliceerd, en zijn bewijs stond tien jaar voordat Percy Heawood (1861-1955) aantoonde dat er een belangrijke fout was in de bewijsmethode die Kempe had gebruikt.


Alfred Kempe (1849-1922), PeterGuthrie Tait (1831-1901) en Percy Heawood (1861-1955) in 1880 was P. G. Tait (1831-1901) een wiskundig natuurkundige, die een oplossing voor het probleem aanbood. Onafhankelijk daarvan had Tait vastgesteld dat kaarten waar een even aantal grenslijnen elkaar op elk punt ontmoeten,met twee kleuren konden worden gekleurd, hoewel dit resultaat eerder in Kempe ‘ s papieren was verschenen.in 1876-77 werd Tait bekend door zijn studie en classificatie van knopen. In die tijd waren er een aantal verschillende theorieën over de structuur van atomen. William Thompson (later Lord Kelvin 1824-1907), geïnspireerd door de experimenten van de Duitse natuurkundige Hermann von Helmholtz (1821-1894), stelde atheorie voor dat atomen buizen van ether waren geknoopt. Kelvin ’s theorie van’ Vortex atomen ‘ werd serieus genomen voor ongeveer twintig jaar, en het inspireerde Tait om een classificatie van knopen ondernemen. Tait, Thomson en James Clark Maxwell (1831-1879) vonden tijdens hun studies vele topologische ideeënuit. Kelvin ’s theorie was echter fundamentallymistaken en natuurkundigen verloren interesse in Tait’ s werk.


Hermann von Helmholtz (1821-1879),Lord Kelvin (1824-1907) en James Clark Maxwell (1831-1879)

Tait begon met de wijze waarop asingle gesloten lus van het koord kan worden geknoopt. Hij had in het begin geen systematische methode en begon op een intuïtieve manier door een enkele gesloten lus te nemen en te experimenteren met de manieren waarop deze kon worden geknoopt. Natuurlijk moest het koord open zijn (zoals ashoelace) dan geknoopt, en verbonden. Merk op dat als je het koord rond de knoop volgt, de ‘over – onder’ kruisingen afwisselen.Vervolgens experimenteerde hij met twee lussen en de manieren waarop ze aan elkaar konden worden geknoopt. Hier zijn knopen met maximaal zes kruisingen voor een enkele lus te zien.
een van de uitkomsten van Tait ‘ s studie was zijn Hamiltoniaanse grafiek vermoeden.
een afbeelding wordt beschouwd als een veelvlak dat op een bol is getekend en kan dan op een vlak worden geprojecteerd. Tait stelde voor dat elke cubicpolyhedral kaart een Hamiltoniancycle heeft . Tait ‘ s methode richtte zich op de randen van de grafiek en hij toonde aan dat een Hamiltoniaanse cyclus een vierkleurige kaart kon produceren. Pas in 1946 vond William Tutte (1917-2002) het eerste tegenvoorbeeld van Tait ‘ s vermoeden.Tait begon in 1880 met de studie van snarks, toen hij bewees dat de vierkleurstelling gelijk was aan de stelling dat geen snark isplanar is. Een vlakke grafiek is er een die in het vlak kan worden getekend zonder randen te kruisen. Het lijkt erop dat Tait ‘ s idee van niet-vlakke grafieken afkomstig is van zijn studie van knopen en Hamiltoniaanse paden .de eerste bekende snark was de Petersen-grafiek die in 1898 werd ontdekt,en wiskundigen begonnen op Meer van dit soort grafieken te jagen, maar pas in 1946 werd een andere snark gevonden.
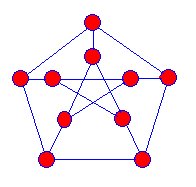 |
Snarks are projections of three dimensional grafieken op het vlak. Er zijn geen hoekpunten waar de Blauwe randen elkaar lijken te kruisen. Snarks hebben de volgende eigenschappen:
|
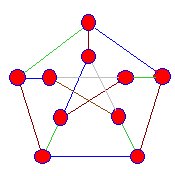 |
de randen die aan de hoekpunten van deze snark voldoen,zijn blauw, groen en bruin gekleurd, maar we bereiken altijd een stadium waarin dit proces niet kan worden voortgezet. |
Julius Peterson (1839-1910)
The Hunting of theSnark is een gedicht geschreven door Lewis Carroll, en Martin Gardner noemde deze grafieken SNARKs, omdat ze zo ongrijpbaar waren.
het probleem transformeren en nieuwe methoden vinden.hoewel Heawood in 1890 de grootste fout in Kempe ‘ s bewijsmethode vond, kon hij niet verder gaan met het bewijzen van de vierkleurstelling, maar hij maakte een belangrijke doorbraak en bewees overtuigend dat alle kaarten met vijf kleuren gekleurd konden zijn.
Heawood leverde vele belangrijke bijdragen aan het probleem,waarbij de aandacht werd verlegd van de gebieden van een kaart naar de grenzen daartussen. In 1898 had hij bewezen dat als het aantal edges rond elke regio deelbaar is door 3, de regio ‘ s met Vier Kleuren konden worden gekleurd.
Cauchy ‘ s bewijs van de formule van Euler omvatte ook het idee dat elk net van een veelvlak driehoekig kan worden gevormd door randen aan makenon-driehoekige vlakken toe te voegen tot driehoeken. Vervolgens ontwikkelde hij een procedure waarbij hij de randen een voor een verwijderde, waaruit bleek dat de vorm van Euler bij elke stap kon worden gehandhaafd.
Cauchy ’s bewijs van de formule van Euler
Cauchy’ s 1813 bewijs van de formule van Euler begon met het idee van aprojectie van een veelvlak om een vlaknet te verkrijgen. Hij demonstreerde verder (a) dat elk net een driehoeksmeting kon zijn, en zijn bewijs(b) van Eulers formule werd op dat moment aanvaard.
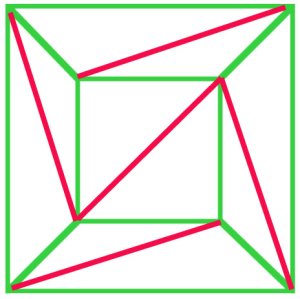 (a)
|
In principle, every polygonal net can be triangulated. In thisnet of a cube (a), $f + v – e$ is $10 + 8 – 17 = 1$, and Euler’sformula still holds. |
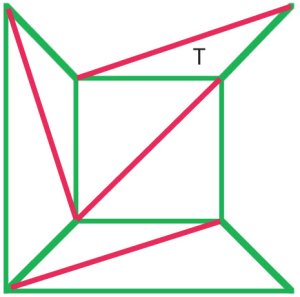 (b)
|
het argument van Cauchy was om de externe randen van diagram(A) een voor een te verwijderen, en toen hij een stadium bereikte zoals in diagram (b)verwijderde de hele driehoek T om de formule van Euler te behouden. Veel math-matici van het begin van de negentiende eeuw waren het erover eens dat deze procedure een bewijs van Eulers formule voor allpolyhedra demonstreerde. |
tegen 1900 wisten wiskundigen dat een planaire grafiek kan worden samengesteld uit elke kaart met behulp van het krachtige concept van dualiteit . In de duale, zijn de regio ‘ s vertegenwoordigd door hoekpunten en twee hoekpunten zijn verbonden door een rand als de gebieden aangrenzend zijn. In deze grafieken vraagt het vermoeden van Vier Kleuren nu of de hoekpunten van de grafiek kunnen worden gekleurd met 4 kleuren, zodat geen twee aangrenzende hoekpunten dezelfde kleur zijn.
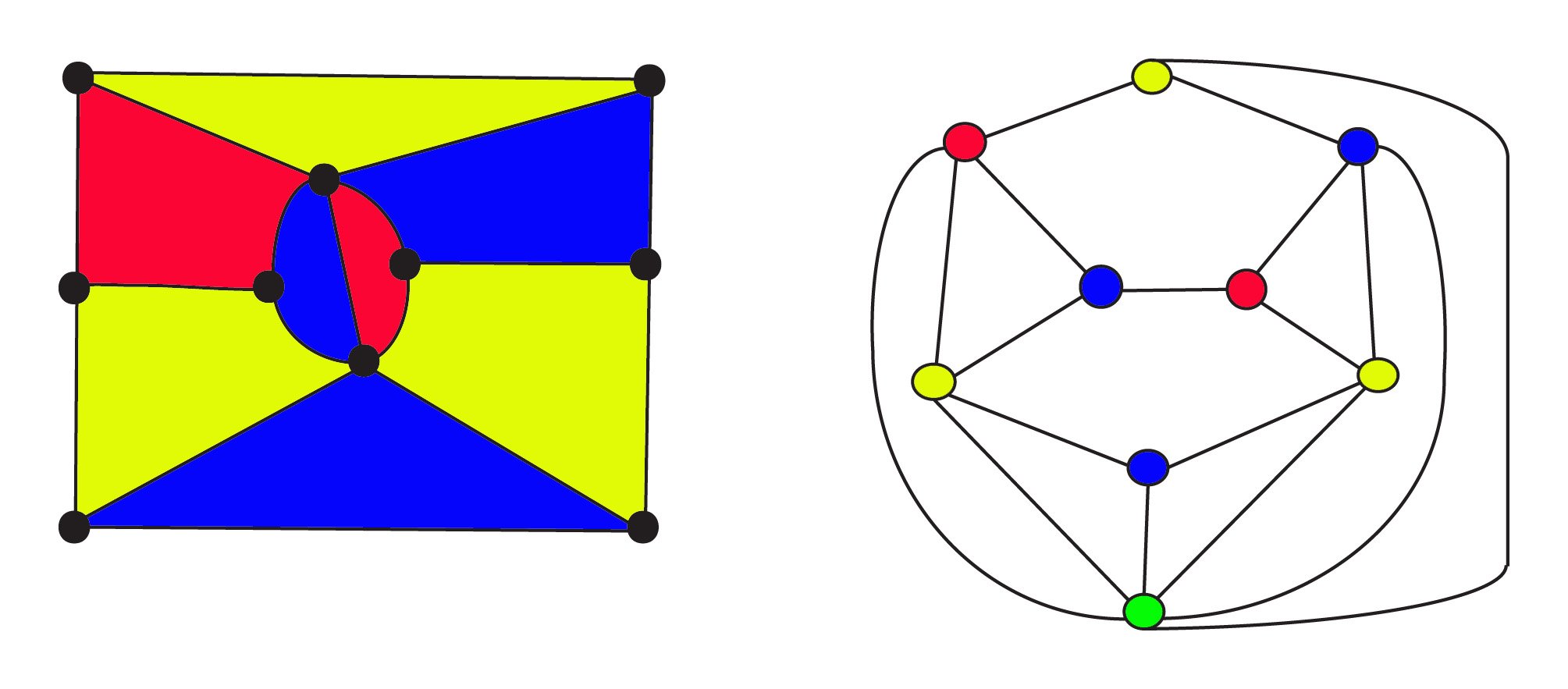
de driekleurige kaart aan de linkerkant heeft$8$ regio ‘ s $10$ hoekpunten en $17$ randen. De dubbele grafiek op het recht heeft$ 9 $ regio ‘ s $9$ hoekpunten en $17$ randen waar de hoekpunten hetzelfde gekleurd zijn als de gebieden van de kaart. De greenvertex aan de onderkant van de Grafiek Vertegenwoordigt de oneindige externe ruimte voor de kaart. Zowel de originele kaart als de duale ervan gehoorzamen Euler ‘sformule voor netwerken $f + v-e = 1 $ of, $ \ text{regio’ s} +\text{hoekpunten} – \text{randen} = 1$. De dualiteitsrelatie is symmetrisch: de dual van de dual zal de oorspronkelijke grafiek zijn, waarbij regio ‘ s en hoekpunten worden uitgewisseld.
gedurende de eerste helft van de twintigste eeuw richtten wiskundigen zich op het wijzigen van dit soort technieken om ingewikkelde kaarten te reduceren tot speciale gevallen die geà dentificeerd en geclassificeerd konden worden, om hun specifieke eigenschappen te onderzoeken en ontwikkelden ze het idee van een minimale set van kaartconfiguraties die getest konden worden.
in eerste instantie werd gedacht dat de verzameling bijna 9.000 leden bevatte, wat een enorme taak was,en dus gingen de wiskundigen over tot computertechnieken om algoritmen te schrijven die de test voor hen konden doen. De algoritmen gebruikten gewijzigde versies van Kempe ‘ s oorspronkelijke idee van ketens samen met andere technieken om het aantal leden van de minimale set te verminderen.nadat Kenneth Appeland Wolfgang Haken in 1976 aan de Universiteit van Illinois met John Koch had samengewerkt aan het probleem van de reduceerbaarheid, reduceerde Kenneth Appeland het testprobleem uiteindelijk tot een niet te voorkomen verzameling met 1.936 configuraties, en een volledige oplossing voor het vermoeden van Vier Kleuren werd bereikt. Dit probleem van het één voor één controleren van de reduceerbaarheid van de kaarten werd dubbel gecontroleerd met verschillende programma ‘ s en verschillende computers. Uit hun bewijs bleek dat ten minste één kaart met een zo klein mogelijk aantal regio ‘ s met vijf kleuren niet kan bestaan.
sinds het eerste bewijs zijn efficiëntere algoritmen gevonden voor kaarten met vier kleuren en tegen 1994 was de onvermijdelijke set configuraties teruggebracht tot 633.
Is een ‘Proof’ gedaan op een Computer een goed bewijs?
omdat het bewijs met behulp van een computer werd gedaan, was er onmiddellijk protest. Veel wiskundigen en filosofen beweerden dat het bewijs niet legitiem was. Sommigen zeiden dat bewijzen alleen door mensen moeten worden ‘bewezen’, niet door machines, terwijl anderen, van een meerpraktische geest, vraagtekens zetten bij de betrouwbaarheid van zowel de algoritmen als het vermogen van de machines om ze foutloos uit te voeren.Veel van de bewijzen die door wiskundigen zijn geschreven, zijn echter fout bevonden, dus het argument over betrouwbaarheid lijkt leeg.Wat de meningen ook waren, de situatie leidde tot een ernstige discussie over de aard van het bewijs, die vandaag nog steeds voortduurt.
voor pedagogische notities:
gebruik het tabblad Notities bovenaan dit artikel of klik hier .
Notes
- meer details over dit en de andere procedures die in dit deel worden gevonden, zijn te vinden in Robin Wilson ‘ s boek Four Colours sufficient .
- knopen kunnen linkshandig of rechtshandig zijn, en tegenwoordig zijn er belangrijke toepassingen van deze eigenschap in de chemie,farmacie, biologie en fysica. (Zie Pedagogische aantekeningen)
- genoemd naar William Rowan Hamilton (1805-1865). Een Hamiltoniaanse pad in een grafiek bezoekt elk vertex precies één keer. Een Hamiltoniaanse cyclus (of circuit) is apath die elk hoekpunt precies één keer bezoekt en terugkeert naar het beginpunt.(Zie Pedagogische aantekeningen)
- het boek van Imre Lakatos, Proofs and Refutations heeft een discussie en kritiek op Cauchy ’s procedure (pagina’ s 6 – 12), en veel meer over het verhaal van de Stelling van Euler.het idee van dualiteit ontstond in de 16e en 17e eeuw met ontwikkelingen in de projectieve meetkunde. Wiskundigen als Pascal endesargues vonden dat nieuwe stellingen gevonden konden worden door de termen ‘punt’ en ‘lijn’ uit te wisselen in beschrijvingen van bepaalde meetkundige configuraties. Een voorbeeld is in regelmatige veelvlakken, waar devertices van de ene overeenkomen met de gezichten van de andere. Dus het Dual van een tetraëder is een andere tetraëder, en het dual van een kubus is een octaëder. De dual van de dual is de originele polyeder.
het beste populaire, gemakkelijk te lezen boek over de vier Colortheorem is:
Wilson, R. (2003)
Four Colours sufficient.Londen.Londen. Pinguïn Boeken.
For a more detailed and technical history, The standardreference book is:
Biggs, N.; Lloyd, E. & Wilson, R. (1986) (1998)
Graph Theory,1736-1936
Oxford. Oxford University Press.
deze brengt ons up-to-date, met meer recente foundations en filosofie.Fritsch, R and Fritsch, G (2000) The Four Color Theorem: History,Topological Foundations, and Idea of Proof New York. Springer-Verlag.
nauwelijks een algemeen geschiedenisboek heeft veel over het onderwerp, maar het laatste hoofdstuk in Katz genaamd ‘Computers and Applications’ heeft een sectie op de grafentheorie, en de vier kleurstelling wordt met veel woorden genoemd.
Polya G. hoe SolveIt.
Dit is het klassieke boek over probleemoplossing. Er zijn veel edities van dit boek sinds het voor het eerst verscheen in de jaren 1950 en het is nog steeds gemakkelijk verkrijgbaar. Vreemd genoeg hebben recente edities de ondertitel ‘a new aspect of Mathematical Method’gekregen.Lakatos, I. (1976) Proofs andrafutations: The Logic of Mathematical Discovery.Cambridge. C. U. P. dit is een ander belangrijk boek dat leidde tot het onderzoek intoProblem Solving and Investigations in de jaren 1970. Het begint als een klaslokaaldiscussie tussen een leraar en een groep studentenover het bewijs van Eulers formule, en loopt door de ideeën,bezwaren en mogelijkheden die in de negentiende eeuw daadwerkelijk door deathematici en wetenschappers werden besproken. Het brengt enkele van de belangrijkste kwesties aan de orde op het gebied van onderwijs en leerproblemen en op het gebied van wiskundige methoden en bewijs.
gerelateerde referenties
Ik heb al enige tijd een boekje over Stringspellen. Toen ik op school zat, heette het Cat ‘ s Cradle, en we speelden het in onze pauze.
onlangs heeft een Frans tijdschrift een paper gepubliceerd over de “algebra” van tekenreeksfiguren! Als je naar Amazon gaat vind je anice boek van Ann Swain en Michael Taylor genaamd Finger Strings: a Book of Cats Cradles andString Figures dat in September 2008 door Floris books zal worden gepubliceerd. Er zijn ongeveer 80 figuren beschreven met gekleurde diagrams.It ‘ s spiraal gebonden, dus het zal open blijven terwijl je de instructies te volgen. Het komt ook met een paar string loops!
voor knoopexperts is het AshleyBook of Knots een klassieker voor iedereen die geïnteresseerd is in de knopen van verschillende soorten knopen en hun gebruik. Amazon heeft verschillende edities beschikbaar tegen verschillende prijzen.
weblinks
voor een algemeen overzicht en links naar veel mensen en onderwerpen is de website van de producent
en natuurlijk zijn biografieën van degenen die betrokken zijn bij de ontwikkeling van alle verschillende wiskundige aspecten te vinden op de index van de biografieën van MacTutor.
De vier kleurstelling en drie bewijzen. Voor de wiskundig persistent heeft de volgende website een intrigerende nieuwe aanpak om het probleem aan te pakken van het construeren van een nieuw algoritme voor het oplossen van het probleem, en koppelverkoop om de afhankelijkheid van een computer te verminderen.http://www.emu.edu.tr/~cahit/the%20four%20color%20theorem%20—%20three%20proofs.htm
voor de Grafiektheorie geeft Wikipedia Een goed overzicht, en je kunt de echt technische dingen overslaan. Het toont de soorten moderne toepassingen van dit gebied van de wiskunde. Als u naar GraphColouring gaat en op de vier kleurstelling klikt, dan vindt u veel meer informatie.een interessante, en niet al te Technische geschiedenis van de Knopentheorie-hoe een idee uit Kelvin ‘ s fysica terugkeert naar de atoomtheorie van vandaag.
De Vereniging van wiskundeleraren heeft Keltische Knotdesign posters. Ga naar hun website en blader door de alfabetische lijst van middelen.
ontdek alles over knopen op de Knoopatlas! Als je geen expert bent – geniet gewoon van de verscheidenheid en complexiteit van de database “The spirit of wiki”
meer artistiek en kleurrijk – maar niet minder wiskundig is de knot Plot Site.
voor degenen die wat van het originele materiaal en historicaldetail willen, Ga naar de geschiedenis van de Knopentheorie op: