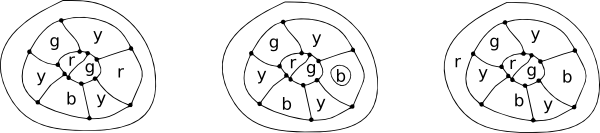
The Four Color Theorem
The Four Color Formodning ble først uttalt litt over 150 yearsago, og endelig viste seg endelig i 1976. Det er en eneståendeeksempel på hvordan gamle ideer kombineres med nye funn ogteknikker i ulike fagområder for å gi nyetilnærminger til et problem. Det er også et eksempel på hvordan et tilsynelatende enkelt problem ble antatt å være ‘løst’, men ble da mer komplekst, og det er det første spektakulære eksempelet der en datamaskin var involvert i å bevise en matematisk teorem.
I Begynnelsen
den formodning at noen kart kan becoloured bruker bare fire farger først dukket opp i et brev fromAugustus De Morgan (1806-1871), første professor i matematikk ved the new University College London, til sin venn William RowanHamilton (1805-1865) den berømte Irske matematikeren i 1852. Det hadbeen foreslått Til De Morgan av En av hans studenter, FrederikGuthrie, på vegne av sin eldre bror Francis (som senere bleprofessor i matematikk Ved University Of Cape Town).


Augustus De Morgan (1807-1871) ogwilliam Rowan Hamilton (1805-1865)
problemet, så enkelt beskrevet, men så tantalizingly vanskeligå bevise, fanget fantasien til mange matematikere påtid. På slutten Av 1860-tallet Tok De Morgan selv problemet og hansprøven Til Amerika hvor Blant Annet Benjamin Peirce (1809-1880) afamous matematiker og astronom, ble interessert i det som borte for å utvikle sine logiske metoder.
De Morgan brukte det faktum at i et kart med fire regioner, hverberører de andre tre, en av dem er helt omsluttet avandre. Siden han ikke kunne finne en måte å bevise dette på, brukte han detsom et aksiom, grunnlaget forhans bevis.
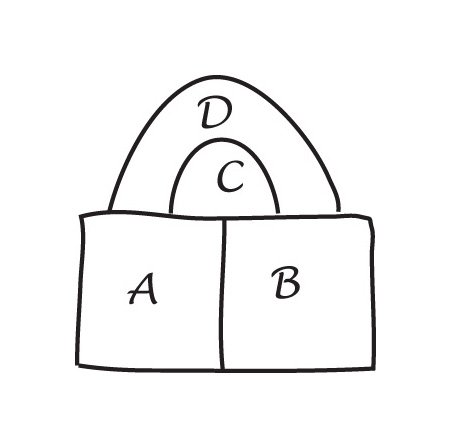
en kopi Av De Morgans originalsketch i sitt brev Til Hamilton og et enkelt fire fargekart.
I 1878 Arthur Cayley (1821-1895) på et møte I Londonmatematisk Samfunn spurte om noen hadde funnet en løsning førde Morgan opprinnelige spørsmålet, men selv om det hadde vært noen interesse, ingen hadde gjort noen betydelig fremgang. Cayley ble interessert i problemet og i 1879 publiserte en kort paperOn farging av kart hvor han forklarte noen av vanskelighetene i å forsøke et bevis og gjort noen viktige bidrag til måten problemet var tilnærming. Hvis et bestemt kart allerede er farget med fire farger, og vi legger til et annet område,kan vi fortsatt beholde samme farge?’begynte en annen linje ofenquiry som førte til anvendelsen av mathematicalinduction til problemet.

Arthur Cayley (1821-1895)
arthur cayley viste at hvis fourcolours allerede hadde blitt brukt til å farge et kart, og en ny region var lagt til, Var det Ikke alltid mulig å beholde originalfargen.
Ovenfor har alle fire fargene blitt brukt på det opprinnelige kartet, og en ny region er trukket for å omgir den. I dette tilfellet er en rød regionendret til blå, slik at rød kan brukes på den nye surroundingregion.
Cayley observert også at det var mulig å løse en versjon av problemet ved å begrense måten grensene møtte. For eksempel, kart der bare tre land møttes har tre kanter møte på avertex. Disse kalles ‘kubikk kart’, og kartene som brukes i thefollowing diskusjon er alle kubikk kart. Også, hvis et kart kan becoloured med fire farger, vil bare tre farger vises på grensen.
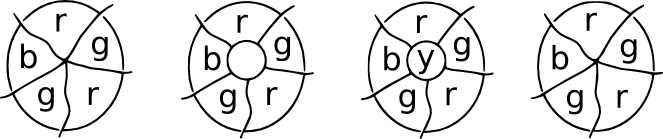
Demonstrasjonen Av Oppdateringen. Tenk deg detpå et sted i et kart møtes en rekke land på et punkt. Nålegg en lapp over møtepunktet, og alle de nye møtepunktenevil ha tre grenser som kommer fra dem. Disse er kubiske kart, og en fjerde farge kan brukes til den sentrale regionen. Ved fjerning av plasteret kan vi gå tilbake til den opprinnelige fargen.
noen gamle teknikker, nye forhold og flere problemer!
for å følge utviklingen av problemet må viundersøke kort noen av ideene, prosedyrene og teknikkeneat matematikere utviklet seg i deres forsøk på å løse det.
The Only Five Neighbours Conjecture
‘hvis du ikke kan løse aparticular problem, finne en enklere en som du kan løse.'(Polya. Hvordan Løse Det)
‘Hvert kart har minst ett land med fem eller færre naboer.’
Tenk deg et kart over en øy omgitt av havet. Ifarge av landene på øya, teller vi havet som enregion. Noen land kan ha bare to grenser (en digon), noetre (som i en trekant), noen fire (en firkant) og noen fem (apentagon) eller mer.
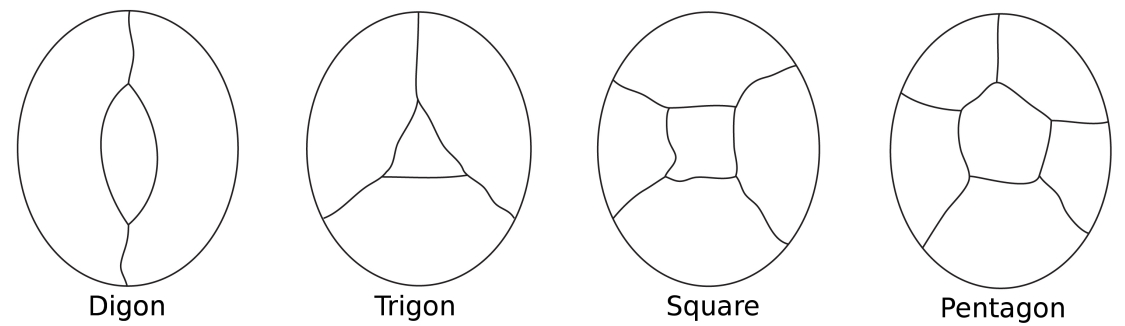
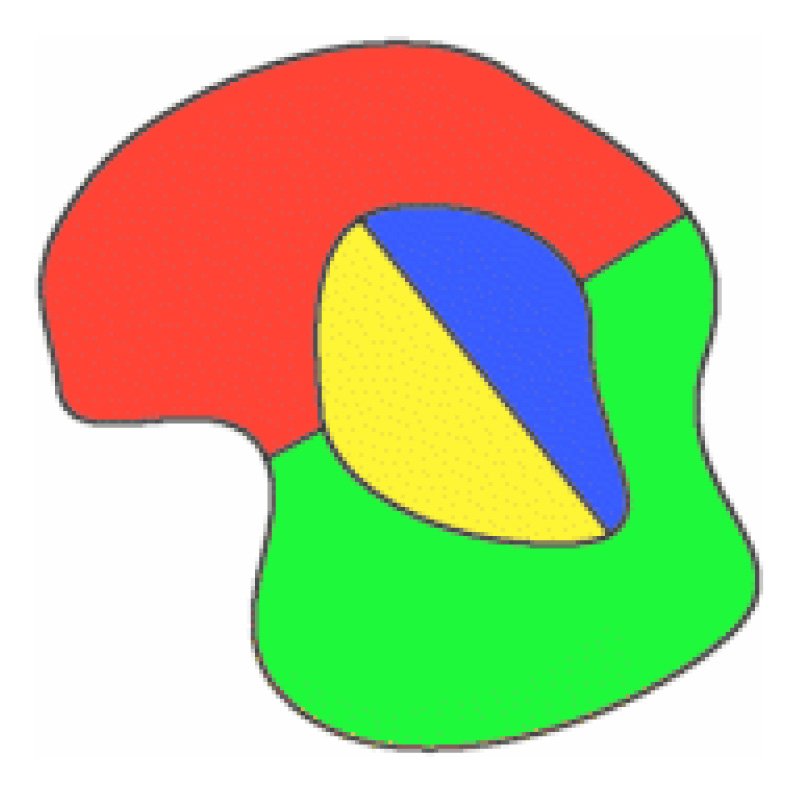
den enkleste muligkonfigurasjoner for å omgi en sentral region.
Merk at i alle disse konfigurasjonene har hver node bare trekanter.
I 1813 ble eulers formel for polyeder tilpasset to dimensjoner av Augustin Cauchy (1759-1857) ved å projisere polyederet på et plan og dermed danne nettet av solid. På denne måten ble formelen $f + v-e = 1$, fordicauchy teller ikke ‘utenfor’ regionen av nettet.

Augustin Cauchy (1759-1857)
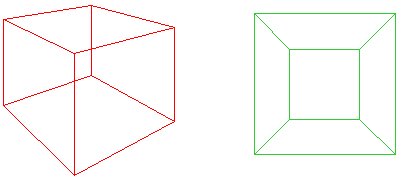
tenk deg å knuse den røde kuben ned på et fly slik at basen åpnes for å danne utsiden av Det Grønne Nettet. Cauchys ide var å kutte ut et ansikt avcube, slik at for et fly polygon, $f + v-e = 1$. Alternativt, hvis’ utsiden ‘ av nettet betraktes som et ansikt med infinitearea, har vi fortsatt $f + v – e = 2$
Vi kan anta at det er minst tre grenselinjer (kanter)som kommer fra hvert møtepunkt (hjørner).
beviset på at kartet har minst ett land omgitt avfem eller færre naboer fortsetter ved motsetning. Hvis dette fører til en absurditet, har vi et bevis.legg nå disse verdiene inn I eulers formel: $ $ f + v-e = 2$ $ ogvi har $$1/3 ( e) + 2/3 (e) – e$$ som er null!
dette er absurditeten, så vår opprinnelige antagelse var falsk.Dette betyr at det må være minst ett land med fem eller færre naboer!
Minimal Kriminelle!
En annen måte å takle fire farge problemet er å anta det isfalse, og se hvor dette fører. Anta at det er kart som trengerfem farger eller mer, og vi velger kartene med de minstemulig antall land. Disse kartene kalles minimale moteksempler ellerminimale kriminelle !
så dette betyr at en minimal kriminell ikke kan farges med fire farger, men et kart med færre land kan farges med fire farger. Hvis vi kan vise at minimale kriminelle ikke kan eksistere, kan vi kanskje gjøre noe fremgang.
For eksempel kan vi vise at en minimal kriminell ikke kan inneholdeen digon.
fra det opprinnelige kartet, ta bort en grense fra digon, ogvi får et nytt kart med færre land. Dette kartet kan være fargetmed fire farger (fra vår antagelse). Vi farger da denne newmap ,( vi trenger bare to farger). Nå erstatte grensen vi fjernet, og re-farge kartet. Vi har brukt tre farger, og siden det fortsatt er en farge tilgjengelig, viser dette at kartet vårt kan være farget med fire farger. Men dette er mot vår antagelse, så en minimal kriminell kan ikkeinneholder en digon.
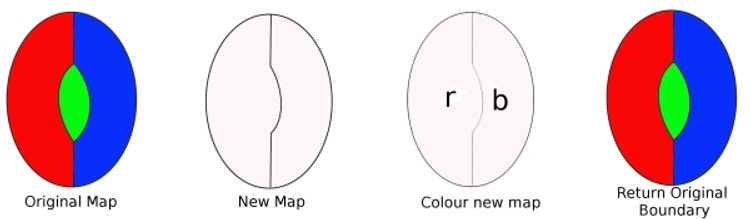
for å vise At En Minimal Kriminellkan ikke inneholde en region med to kanter (en digon). Anta at det eren minimal kriminell som inneholder en digon. Fjerne en kant betyrkartet inneholder færre regioner. Så dette nye kartet kan være fargetmed fire farger. Erstatt nå den tapte kanten. Siden bare to farger var nødvendig før, erstatte kanten betyr at vi kan bruke athird farge, og har fortsatt en fjerde farge å bruke. Så, en minimalkriminal kan farges med fire farger. Derfor kan en minimalkriminal ikke inneholde en digon.
denne prosedyren kan gjentas for å vise at en minimal kriminellkan ikke inneholde et tresidig land( en trigon), men det bryter nednår vi prøver teknikken på en firkant, fordi når vi erstatter thesquare, kan landene ved siden av det godt bruke alle fourcolours, så bevisprosedyren mislykkes. Når dette har skjedd, blir det åpenbart at det ikke vil fungere for pentagoner, og så videre.
Six Colour Theorem
en lignende teknikk kan brukes for å vise at six colourtheorem er sant. Først antar vi at det ikke er noen kart som kan værefarget med seks farger. Noen av kartene kan være farget withseven farger, så å velge en av disse (en minimal kriminell), hvis vi kan vise at det er mulig å farge det med mindre enn sevencolours, vi har oppnådd vårt mål.
fra beviset på five neighbours theorem, er det mulig å fortsette å bruke den minimale kriminelle ideen for å vise at et kart kan farges med sixcolours!
Fra Regioner Til Knuter, Nettverk og Topologi
I 1879 Alfred Kempe (1849-1922), ved hjelp av teknikker som ligner på de som er beskrevet ovenfor, startet fra ‘fem naboer eiendom ‘og utviklet en prosedyre kjent som metoden For’ Kempe Kjeder ‘ tilfinn et bevis På De Fire Fargeteoremet. Han publiserte dette beviset iamerikansk Journal Of Mathematics. Han fant to enklere versjoner som ble publisert i neste år, og hans bevis sto for tenyears før Percy Heawood (1861-1955) viste det var animportant feil i proof-metoden Som Kempe hadde brukt.


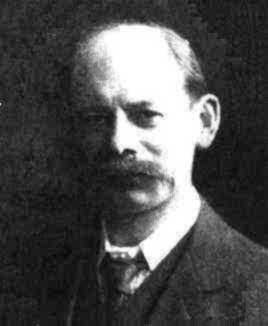
Alfred Kempe (1849-1922), PeterGuthrie Tait (1831-1901) og percy heawood (1861-1955)
i 1880 p. g. tait (1831-1901) en matematisk fysiker, tilbysen løsning på problemet. Uavhengig, Tait hadde etablert thatmaps hvor et likt antall grenselinjer møtes på hvert punkt, kan være farget med to farger, selv om dette resultatet hadappeared tidligere I Kempe papirer.
I Løpet Av 1876-77 Ble Tait kjent for sin studie ogklassifisering av knuter. På den tiden var det en rekkeforskjellige teorier om atomenes struktur. William Thompson (Senere Lord Kelvin 1824-1907) inspirert av eksperimenter av den tyske Fysikeren Hermann von Helmholtz (1821-1894) foreslo ateori at atomer var knyttede rør av eter. Kelvins teori om’ forvortexatomer ‘ ble tatt alvorlig i omtrent tjue år, og Det inspirerte Tait Til å foreta en klassifisering av knuter. Tait, Thomsonog James Clark Maxwell (1831-1879) oppfunnet mange topologiske ideerunder sine studier. Kelvins teori var imidlertid fundamentaltfeil og fysikere mistet interessen For Taits arbeid.


Hermann von Helmholtz (1821-1879),Lord Kelvin (Engelsk) 1824-1907) og james clark maxwell (1831-1879)

tait begynte med måtene som asingle lukket sløyfe av ledningen kan knyttes. Han hadde ingen systematicmethod i starten, og begynte på en intuitiv måte ved å ta asingle lukket sløyfe og eksperimentere med hvordan det kunne knyttes. Selvfølgelig måtte ledningen være åpen (som ashoelace) så knutet og sluttet seg til. Merk at hvis du følger thecord rundt knuten, vil’ over – under ‘ kryssinger alternere.Han fortsatte med å eksperimentere med to løkker og måtene de kunne knyttes sammen. Vist her er knuter med opptil sekscrossings for en enkelt sløyfe.
Et av resultatene Av Taits studie var Hans Hamiltonian graph formodning.Et kart betraktes som en polyeder tegnet på en sfære, og det kan deretter projiseres på et fly. Tait foreslo at ethvert cubicpolyhedral-kart har En Hamiltoniancycle . Taits metode fokuserte på kantene på grafen oghan viste at En Hamiltonian syklus kunne produsere en firefarging av et kart. Det var ikke Før 1946 At William Tutte (1917-2002) fantdet første moteksemplet Til Taits formodning.
Tait og forbindelsen med knuter
Taitinitiated studiet av snarks i 1880, da han viste at fourcolour teoremet var ekvivalent med påstanden om at ingen snark isplanar. En plan graf er en som kan tegnes i flyet medingen kanter krysser. Det ser ut Som Om Taits ide om ikke-plan graphsmight har kommet fra hans studie av knuter og Hamiltonian stier .Den første kjente snark Var Petersen grafen oppdaget i 1898, og matematikere begynte å jakte på flere av disse typer grafermen det var ikke før 1946 at en annen snark ble funnet.
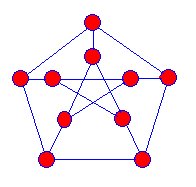 |
snarks er projeksjoner av tredimensjonale grafer på theplane. Det er ingen hjørner der de blå kantene ser ut til å krysshverandre. Snarks har følgende egenskaper:
|
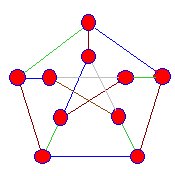 |
kantene som møter hjørnene i denne snark er farget blå, grønn og brun, men vi når alltid et stadium der denne prosessenkan ikke videreføres. |

Julius Peterson (1839-1910)
jakt på thesnark er et dikt skrevet av lewis carroll, og martin gardnerkalt disse grafene snarks, fordi de var så unnvikende.
Transformere problemet og finne nye metoder.
Selv Om Heawood fant den store feilen I Kempes bevismetode i 1890, var Han ikke i stand til å fortsette å bevise de fire fargeteoremet, men han gjorde et betydelig gjennombrudd og viste at alle kartene kunne være farget med fem farger.Heawood gjorde mange viktige bidrag til problemet,og skiftet fokus fra områdene på et kart til grensene mellom dem. I 1898 hadde han bevist at hvis antallkanten rundt hver region er delbar med 3, kunne regionene være farget med fire farger.Cauchys bevis på eulers formel inkluderte også ideen om at et hvilket som helst nett av et polyeder kan trianguleres ved å legge kanter til makenon-trekantede ansikter i trekanter. Han utviklet deretter en prosedyre hvor han slettet kantene en etter en, og viste At Euler ‘ sformula kunne opprettholdes ved hvert trinn.
Cauchys Bevis på Eulers Formel
Cauchys 1813-bevis på Eulers Formel begynte med ideen om aprojeksjon av et polyeder for å oppnå et plannett. Han demonstrerte (a) at et hvilket som helst nett kunne trianguleres, og hans bevis(b) på Eulers Formel ble akseptert på den tiden.
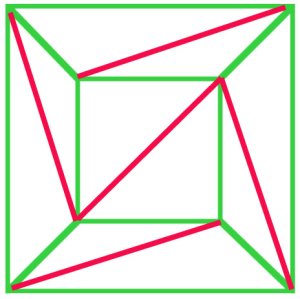 (a)
|
In principle, every polygonal net can be triangulated. In thisnet of a cube (a), $f + v – e$ is $10 + 8 – 17 = 1$, and Euler’sformula still holds. |
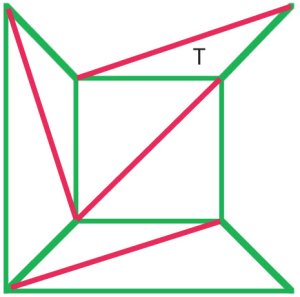
(b)
|
cauchy argument var å fjerne de ytre kanter fra diagrammet(a) en etter en, og da han nådde et stadium som i diagrammet (b)fjernet hele trekanten t, og dermed bevare eulers formel. Mangematematikere fra det tidlige nittende århundre ble enige om at detteprosedyren viste et bevis På eulers formel for allpolyhedra. |
innen 1900 visste matematikere at en plan graf kan værekonstruert fra et hvilket som helst kart ved hjelp av det kraftige konseptet dualitet . I dual, deregioner er representert av hjørner og to hjørner er forbundet meden kant hvis regionene er tilstøtende. I disse grafene spør FourColour-Formodningen om grafens hjørner kan bli farget med 4 farger, slik at ingen to tilstøtende hjørner er samme farge.
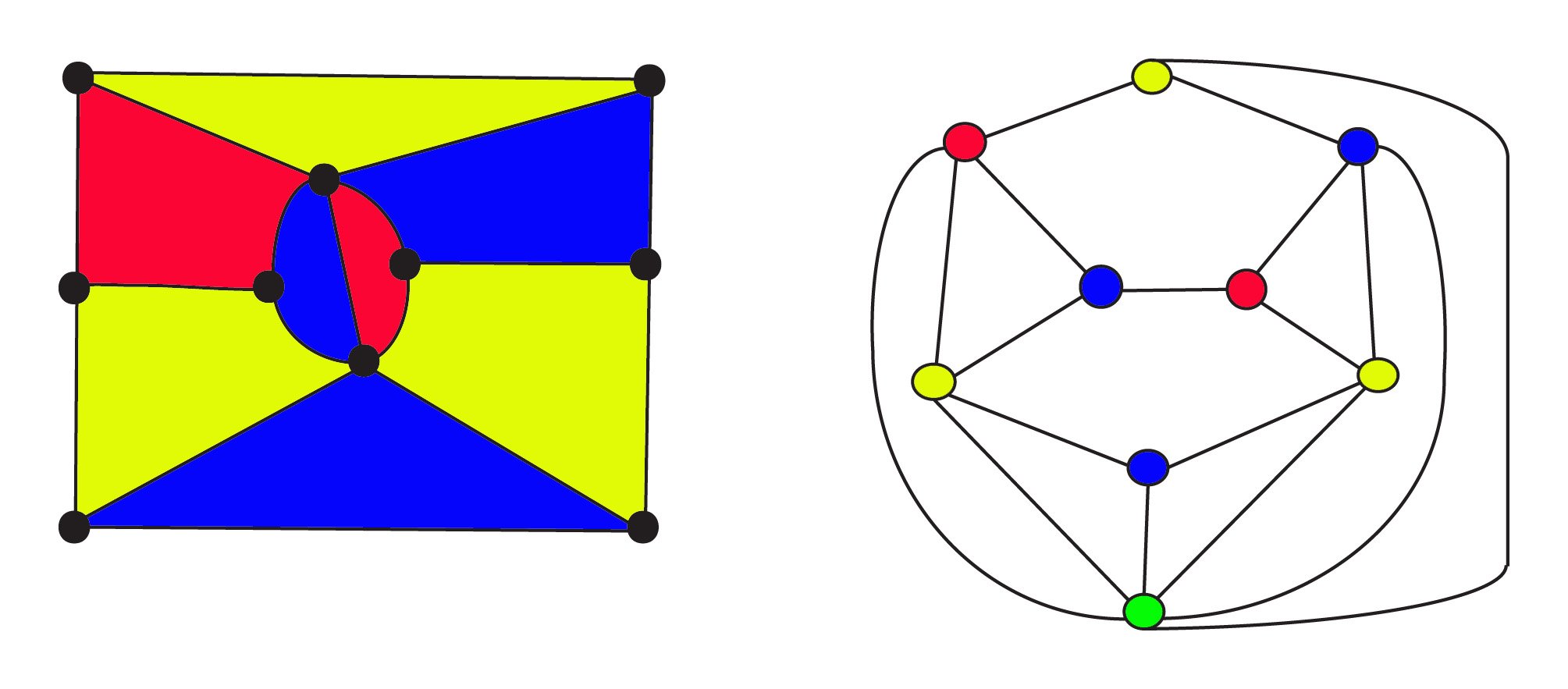
det 3-fargede kartet til venstre har $8 $ regioner $ 10 $ hjørner og $17$ kanter. Dens dobbelgraf på theright har $9 $ regioner$ 9 $hjørner og$ 17 $ kanter hvor toppene er farget på samme måte som områdene på kartet. Greenvertexen nederst i grafen representerer det uendelige eksterneområde for kartet. Både det opprinnelige kartet Og dets dual obey Euler ‘ formula for nettverk $f + v-e = 1 $ eller $\text{regions} + \ text{vertices}- \ text{edges} = 1$. Dualitetsforholdet ersymmetrisk: dual av dual vil være den opprinnelige grafen, hvorregioner og hjørner utveksles.
i løpet av første halvdel av det tjuende århundre, matematikere fokusert på å endre slike teknikker for å redusere kompliserte kart til spesielle tilfeller som kan identifiseres ogklassifisert, for å undersøke deres spesielle egenskaper og utviklet ideen om et minimalt sett med kartkonfigurasjoner som kunne testes.i første omgang ble settet antatt å inneholde nesten 9.000 medlemmer som var en enorm oppgave, og så matematikerne vendte seg til datateknikker for å skrive algoritmer som kunne gjøre thetesting for dem. Algoritmene brukte modifiserte versjoner Av Kempesoriginal ide om kjeder sammen med andre teknikker for å redusereantall medlemmer av minimumssettet.Etter å ha samarbeidet Med John Koch om problemet med reduserbarhet, i 1976 ved University Of Illinois, reduserte Kenneth Appelland Wolfgang Haken til slutt testproblemet til anunavoidable sett med 1,936 konfigurasjoner, og en komplett løsning på De Fire Fargeforutsetningene ble oppnådd. Dette problemet medkontroll av reduksjon av kartene en etter en ble dobbeltsjekketmed forskjellige programmer og forskjellige datamaskiner. Deres bevis viste at minst ett kart med minst mulig antall regioner som krever fem farger, ikke kan eksistere.Siden det første beviset har mer effektive algoritmer blitt funnet for 4-fargekart og i 1994 hadde det uunngåelige settet avkonfigurasjoner blitt redusert til 633.
Er Et’ Bevis ‘ Gjort på En Datamaskin Et Riktig Bevis?
fordi beviset ble gjort ved hjelp av en datamaskin, var deten umiddelbar ramaskrik. Mange matematikere og filosofer hevdetat beviset ikke var legitimt. Noen sa at bevis burde ikke være ‘bevist’ av mennesker, ikke maskiner, mens andre, av et merpraktisk sinn spurte påliteligheten til både algoritmene og maskinens evne til å utføre dem uten feil.Imidlertid har mange av bevisene skrevet av matematikere værtfunnet å være feil, så argumentet om pålitelighet virker tomt.Uansett meninger uttrykt, ga situasjonen en alvorligdiskusjon om bevisets natur som fortsatt fortsetterdag.
for pedagogiske notater:
Bruk notater-fanen øverst i denne artikkelen eller klikk her .
Notater
- Flere detaljer om dette og de andre prosedyrene som finnes i denne delen kan ses I Robin Wilsons bok Four Colours Enough .
- Knuter Kan være venstrehåndet eller høyrehendt, og i dag er detviktige anvendelser av denne egenskapen innen kjemi, apotek,biologi og fysikk. (Se Pedagogiske Notater)
- Oppkalt Etter William Rowan Hamilton (1805-1865). En Hamiltonian bane i en graf besøkhver toppunkt nøyaktig en gang. En Hamiltonian syklus (eller krets)er apath som besøker hvert toppunkt nøyaktig en gang og vender tilbake til startpunktet.(Se Pedagogiske Notater)
- boken Av Imre Lakatos, Proofs and Refutations har adiskusjon og kritikk Av Cauchy prosedyre (sider 6 – 12), ogmye mer om historien Om Eulers Teorem.
- ideen om dualitet oppsto i det 16. og 17. århundre medutviklinger i projektiv geometri. Matematikere som Pascal anddesargues fant at nye teoremer kunne bli funnet ved å utveksle vilkårene ‘punkt ‘ og’ linje ‘ i beskrivelser av visse geometricalconfigurations. Et eksempel er i vanlig polyeder, hvorvertices av en tilsvarer ansiktene til den andre. Så dualof en tetraeder er en annen tetraeder, og dual av en kube er et oktaeder. Den dobbelte av dual er originalenpolyhedron.
den aller beste populære, lettleste boken Om De Fire Fargerteoremet er:
Wilson, R. (2003)
Fire Farger Er Nok.London. Penguin Bøker.
For en mer detaljert og teknisk historie, den standardreference boken er:
Biggs, N.; Lloyd, E.& Wilson, R. (1986) (1998)
Grafteori, 1736-1936
Oxford. University Press. S.
denne bringer oss oppdatert, med nyere grunnlag ogfilosofi.
Fritsch, R og Fritsch, G (2000)
De Fire Farger Teoremet: Historie, Topologiske Fundamenter, Og Ideen Om Bevis
New York. Springer-Verlag.
Knapt noen generell historiebok har mye om emnet, men det siste kapittelet I Katz kalt ‘Datamaskiner og Applikasjoner’ har aseksjon på Grafteori, Og Fire Fargeteoremet er nevntto ganger.
Polya G. Hvordan Å SolveIt.
dette er den klassiske boken Om Problemløsning. Det har vært mange utgaver av denne boken siden den først dukket opp på 1950-tallet og det er fortsatt lett tilgjengelig. Merkelig, nyere utgaver har værtgitt underteksten ‘Et nytt aspekt Av Matematisk Metode’.Lakatos, I. (1976) Bevis andRefutations: Logikken I Matematisk Oppdagelse.Cambridge. C. U. P.
Dette er en annen viktig bok som førte til forskning intoproblemløsning og Undersøkelser på 1970-tallet. Det begynner som en klasseromsdiskusjon mellom en lærer og en gruppe studenter om beviset På eulers formel, og spenner gjennom ideene, innvendingene og mulighetene som faktisk ble diskutert avmatematikere og forskere i det nittende århundre. Det øker noen av de viktigste spørsmålene om undervisning og læringsproblemløsning og om matematiske metoder og bevis.
Relaterte Referanser
jeg har hatt en liten bok Om Strengspill i noen tid. Da Jeg var på skolen, ble Det kalt Kattens Vugge, og vi spilte den i vårbryte tid.
Nylig har en fransk journal publisert et papir om ‘algebra’ av strengfigurer! Hvis Du går Til Amazon finner du anice bok Av Ann Swain Og Michael Taylor kalt Finger Strings: A Book Of Cats Vugger Andstring Tall som skal utgis Av Floris books I September2008. Det er noen 80 figurer beskrevet med farget diagrams.It ‘ s spiral bundet, så det vil holde åpent mens du følger instructions. Det kommer også med et par strengløkker!
For knoteksperter er AshleyBook Of Knots en klassiker for alle som er interessert ihundrevis av forskjellige typer knuter og deres bruk. Amazon harulike utgaver tilgjengelig til forskjellige priser.
Web Links
for en generell oversikt og lenker til mange mennesker og emner, theMacTutor nettstedet er
Og Selvfølgelig MacTutor biografier av de involverte iutvikle alle de ulike matematiske aspekter kan bli funnet på The MacTutor Biografier Index.
De Fire Fargeteoremet og Tre Bevis. For matematiskvedvarende har følgende nettsted en spennende ny tilnærming tilangriper problemet med å bygge en ny algoritme for å løseproblemet og binde for å redusere avhengigheten av en datamaskin.http://www.emu.edu.tr/~cahit/the%20four%20color%20theorem%20—%20three%20proofs.htm
For Grafteori gir Wikipedia en god oversikt, og Du kan gå over de virkelig tekniske tingene. Det viser hva slags moderneapplikasjoner av dette området av matematikk. Hvis du går Til GraphColouring og klikker På Four Colour Theorem, vil du finnemye mer informasjon.En interessant, og ikke for teknisk Historie Om Knutteori-hvordan en ide fra Kelvins Fysikk vender tilbake Til Atomteorii Dag.
Foreningen Av Lærere I Matematikk har Celtic Knotdesign plakater. Gå til deres hjemmeside og bla gjennom alfabetiskliste over ressurser.
Finn ut alt Om Knuter på Knuten Atlas! Hvis du ikke er anexpert – bare nyte variasjonen og kompleksiteten i databasen «inthe spirit of wiki»
mer kunstnerisk og fargerik-men ikke mindre matematisk er theKnot Plot Nettstedet.
For de som ønsker noen av de originale ting og historiskedetalj gå Til Historien Om Knute Teori på: