四色定理
四色予想は150年以上前に初めて述べられ、1976年に最終的に証明された。 これは、古いアイデアが新しい発見と数学のさまざまな分野の技術とどのように組み合わせて問題に新しいアプローチを提供するかの顕著な例です。 また、明らかに単純な問題が”解決”されたと考えられていたが、その後より複雑になった方法の例であり、コンピュータが数学的定理を証明することに関与した最初の壮大な例である。
初めに
任意のマップは、唯一の四つの色を使用して着色することができたという推測は、最初にaugustus De Morgan(1806-1871)、ニューユニバーシティ-カレッジ-ロンドンの数学の最初の教授から、彼の友人William RowanHamilton(1805-1865)1852年に有名なアイルランドの数学者への手紙に登場した。 それはHadbeenは彼の兄フランシス(後にケープタウン大学で数学の教授になった)に代わって、彼の学生の一人、FrederikGuthrieによってド-モルガンに提案した。


Augustus De Morgan(1807-1871)andWilliam Rowan Hamilton(1805-1865)
問題は、単純に説明されていますが、そうですtantalizingly difficult証明するには、当時の多くの数学者の想像力をキャッチしました。 1860年代後半、ド-モルガンはこの問題をアメリカに持ち込み、数学者で天文学者でもあったベンジャミン-パース(1809年-1880年)はこの問題に興味を持ち、彼の論理的な方法を開発した。
De Morganは、4つの地域を持つ地図では、それぞれ他の3つに触れると、そのうちの1つは他の地域で完全に囲まれています。 彼はこれを証明する方法を見つけることができなかったので、彼は彼の証明の基礎である公理としてそれを使用しました。
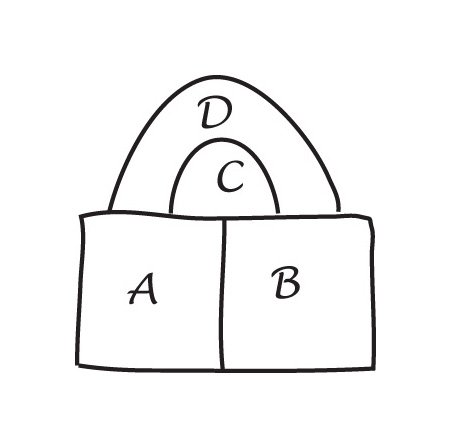
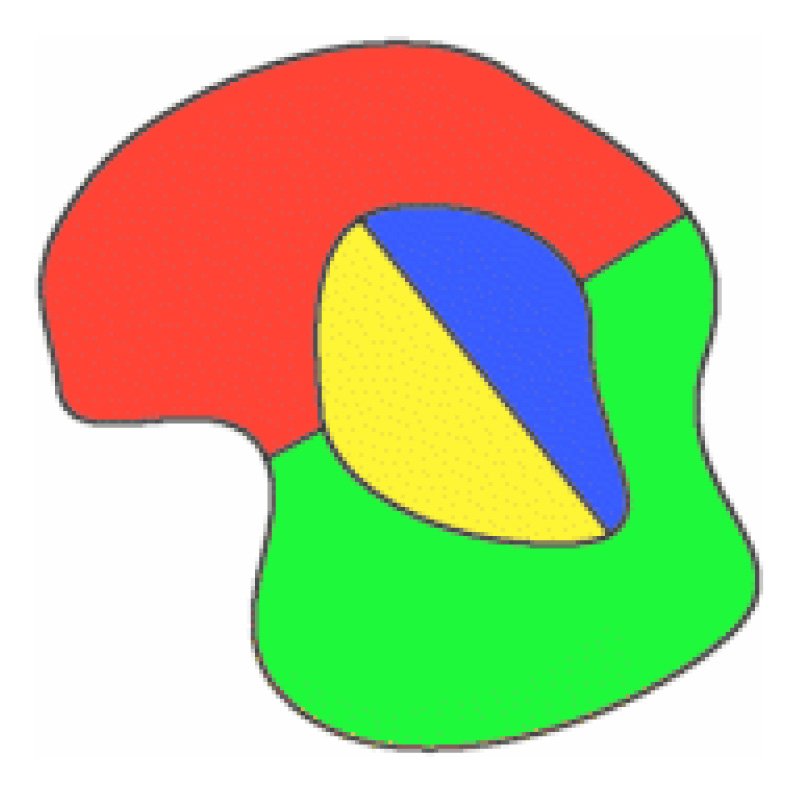
ハミルトンへの手紙のDe Morganのoriginalsketchのコピーとシンプルな四つのカラーマップ。
1878年、アーサー-ケイリー(1821年-1895年)はロンドン数学協会の会合で、誰かがデ-モーガンの元の質問の解決策を見つけたかどうかを尋ねたが、いくつかの関心があったが、誰も大きな進歩を遂げていなかった。 ケイリーはこの問題に関心を持ち、1879年に短い論文を発表した地図の着色彼は証明を試みることの難しさのいくつかを説明し、問題がアプローチされた方法にいくつかの重要な貢献をした。 彼の質問は、”特定の地図がすでに四色で正常に着色されていて、別の領域を追加すると、同じ色を保つことができますか?”問題への数学的誘導の適用につながったofenquiry別の行を始めました。H5>

アーサー-ケイリー(1821-1895)

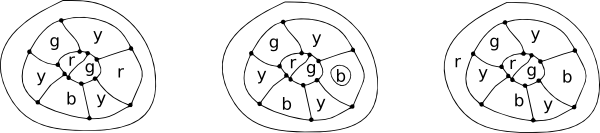
arthur cayleyは、fourcoloursが既にマップの色付けに使用されていて、新しい領域が追加されている場合、元の色付けを維持することは必ずしも可能ではないことを示
上記では、元のマップでは四つの色がすべて使用されており、それを囲むように新たな領域が描かれています。 この場合、赤の領域は青に変更されるため、新しいsurroundingregionで赤を使用できます。Cayleyはまた、境界が満たされる方法を制限することによって、問題のバージョンを解決することが可能であることを観察しました。 たとえば、3つの国が出会った地図には、avertexで3つのエッジが会合しています。 これらは”三次写像”と呼ばれ、以下の議論で使用される写像はすべて三次写像である。 また、マップが四色で着色できる場合、境界線には三色のみが表示されます。
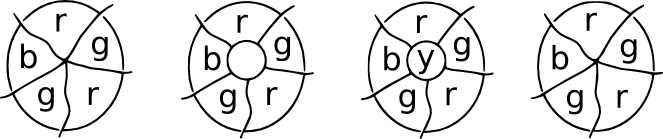
パッチのデモ。 それを想像してみてください地図内のある場所では、いくつかの国がある時点で会います。 今、ミーティングポイントの上にパッチを置くと、すべての新しいミーティングポイントは、それらから発せられた三つの境界を持っています。 これらは立方体の地図であり、中央領域には第四の色を使用することができます。 Removingtheパッチで、私達は元の着色に戻ってもいいです。いくつかの古い技術、新しい条件、およびより多くの問題!
問題の発展に従うためには、数学者がそれを解決しようとする試みで開発したアイデア、手順、技術のいくつかを簡単に調べる必要があります。
唯一の五つの隣人予想
‘あなたがaparticular問題を解決できない場合は、あなたが解決できる簡単なものを見つけてください。’(ポリヤ… それを解決する方法)
‘すべてのマップは、少なくとも一つを持っています五以下の隣人と国。’
海に囲まれた島の地図を想像してみてください。 島の国の色、私たちは海を1つとして数えます地域。 いくつかの国は、2つの境界線(digon)、somethree(三角形のように)、いくつかの4つ(正方形)、およびいくつかの5つ(apentagon)以上を持つことができます。
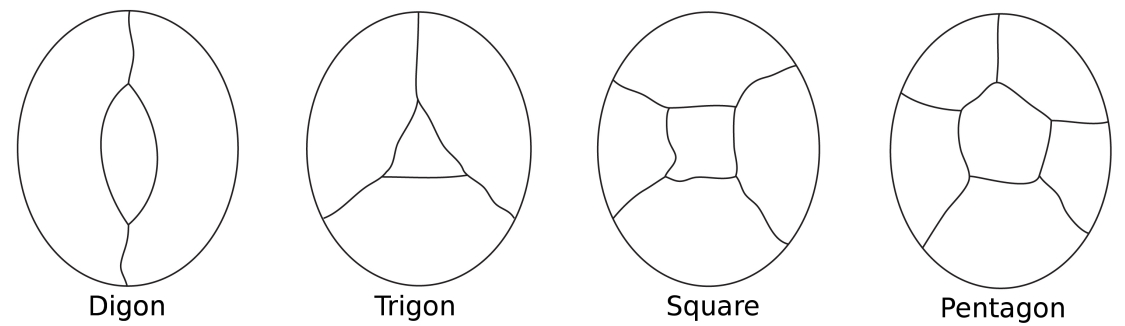
中央領域を囲むための最も簡単な構成。
これらの設定のすべてで、各ノードはthreeedgesのみを持っていることに注意してください。1813年、オーギュスタン・コーシー(1759-1857)によってオイラーの多面体の公式が2次元に適用され、多面体を平面上に投影することによって固体のネットを形成した。 このようにして、式はnet f+v-e=1.になりました。H5>

オーガスティン-コーシー(1759-1857)




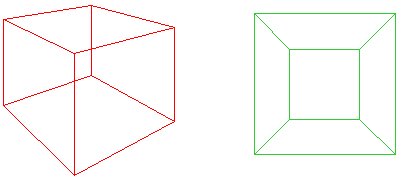
赤い立方体を平面に押しつぶして、その底を開いて緑のネットの外側を形成すると想像してください。 Cauchyのアイデアは、平面多角形の場合、plane f+v-e=1.となるように、立方体の1つの面を切り取ることでした。 代わりに、ネットの「外側」がinfiniteareaの面とみなされている場合、each f+v-e=2
各集合点(頂点)から少なくとも3つの境界線(エッジ)が出
マップに少なくとも一つの国が囲まれていることの証明5つ以下の隣人は矛盾によって進行します。 これが不条理につながるならば、私たちは証拠を持っています。ここで、これらの値をオイラーの式に入れます。f f+v-e=2andとzero1/3(e)+2/3(e)-e zeroはゼロです!これは不条理なので、私たちの元の仮定は間違っていました。
これは不条理です。
これは、少なくとも一つの国が五つ以下の隣人を持つ必要があることを意味します!
最小限の犯罪者!4つの色の問題に取り組む別の方法は、それが偽であると仮定し、これがどこにつながるかを確認することです。
次のようにします。
5つ以上の色が必要なマップがあり、可能な国の数が最も少ないマップを選択するとします。 これらのマップは、最小限の反例または最小犯罪者と呼ばれています!
だから、これは最小限の犯罪者は四つの色で着色することはできませんが、より少ない国の地図は四つの色で着色することができます。
最小の犯罪者が存在できないことを示すことができれば、いくつかの進歩を遂げることができるかもしれません。
たとえば、最小限の犯罪者はディゴンを含めることができないことを示すことができます。
元のマップから、ディゴンから境界を取り除き、より少ない国の新しいマップを取得します。 このマップは、(私たちの仮定から)4色で着色することができます。 次に、このnewmapに色を付けます(必要なのは2色だけです)。 ここで、削除した境界線を置き換え、マップの色を変更します。 私たちは三色を使用しています,そして利用可能なもう一つの色thereisので、,これは私たちのマップは四色でbecolouredことができることを示しています. しかし、これは私たちの仮定に反しているので、最小限の犯罪者はディゴンを含むことはできません。
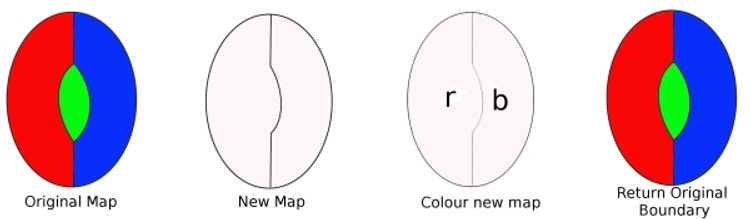
最小の犯罪者には、二つのエッジ(ディゴン)を持つ領域が含まれていることを示します。 ディゴンを含む最小限の犯罪者がいるとします。 エッジを削除すると、マップに含まれるリージョンが少なくなります。 だから、この新しいマップは四色で着色することができます。 今ロストエッジを交換してください。 以前はtwocoloursだけが必要だったので、エッジを交換すると、3番目の色を使用でき、使用する4番目の色を使用できることを意味します。 だから、minimalcriminalは四つの色で着色することができます。 したがって、minimalcriminalにはdigonを含めることはできません。
この手順は、最小限の犯罪者に三面の国(三角)が含まれていないことを示すために繰り返すことができますが、正方形を置き換えると、隣の国がfourcoloursすべてを使用している可能性があるため、証明手順が失敗するため、正方形でテクニックを試してみると破壊されます。 これが起こったら、それは五角形のために動作しません明らかになり、というように。
六色定理
同様の手法を適用して、六色定理が真であることを示すことができる。 まず、六つの色で着色できるマップがないと仮定します。 いくつかのマップは七色で着色することができるので、これらのいずれかを選択する(最小限の犯罪者)、七色未満で着色することが可能であることを示
五隣接定理の証明から、任意のマップがsixcoloursで着色することができることを示すために、最小限の犯罪的な考えを使用してプロセスすることが可能である!
領域から結び目、ネットワーク、トポロジーへ
1879年、アルフレッド-ケンペ(1849年-1922年)は、上記のような技術を用いて、”五つの隣人特性”から始まり、”ケンペ鎖”の方法として知られる手順を開発し、四色定理の証明を見つけた。 彼はこの証明をAmerican Journal of Mathematicsに発表しました。 パーシー-ヒーウッド(1861年-1955年)がケンペが使用していた証明方法に重要な誤りがあることを示す前に、彼の証明は十年のために立っていた。


オーガスティン-コーシー(1759-1857)



赤い立方体を平面に押しつぶして、その底を開いて緑のネットの外側を形成すると想像してください。 Cauchyのアイデアは、平面多角形の場合、plane f+v-e=1.となるように、立方体の1つの面を切り取ることでした。 代わりに、ネットの「外側」がinfiniteareaの面とみなされている場合、each f+v-e=2
各集合点(頂点)から少なくとも3つの境界線(エッジ)が出
マップに少なくとも一つの国が囲まれていることの証明5つ以下の隣人は矛盾によって進行します。 これが不条理につながるならば、私たちは証拠を持っています。ここで、これらの値をオイラーの式に入れます。f f+v-e=2andとzero1/3(e)+2/3(e)-e zeroはゼロです!これは不条理なので、私たちの元の仮定は間違っていました。
これは不条理です。
これは、少なくとも一つの国が五つ以下の隣人を持つ必要があることを意味します!
最小限の犯罪者!4つの色の問題に取り組む別の方法は、それが偽であると仮定し、これがどこにつながるかを確認することです。
次のようにします。
5つ以上の色が必要なマップがあり、可能な国の数が最も少ないマップを選択するとします。 これらのマップは、最小限の反例または最小犯罪者と呼ばれています!
だから、これは最小限の犯罪者は四つの色で着色することはできませんが、より少ない国の地図は四つの色で着色することができます。
最小の犯罪者が存在できないことを示すことができれば、いくつかの進歩を遂げることができるかもしれません。
たとえば、最小限の犯罪者はディゴンを含めることができないことを示すことができます。
元のマップから、ディゴンから境界を取り除き、より少ない国の新しいマップを取得します。 このマップは、(私たちの仮定から)4色で着色することができます。 次に、このnewmapに色を付けます(必要なのは2色だけです)。 ここで、削除した境界線を置き換え、マップの色を変更します。 私たちは三色を使用しています,そして利用可能なもう一つの色thereisので、,これは私たちのマップは四色でbecolouredことができることを示しています. しかし、これは私たちの仮定に反しているので、最小限の犯罪者はディゴンを含むことはできません。

最小の犯罪者には、二つのエッジ(ディゴン)を持つ領域が含まれていることを示します。 ディゴンを含む最小限の犯罪者がいるとします。 エッジを削除すると、マップに含まれるリージョンが少なくなります。 だから、この新しいマップは四色で着色することができます。 今ロストエッジを交換してください。 以前はtwocoloursだけが必要だったので、エッジを交換すると、3番目の色を使用でき、使用する4番目の色を使用できることを意味します。 だから、minimalcriminalは四つの色で着色することができます。 したがって、minimalcriminalにはdigonを含めることはできません。
この手順は、最小限の犯罪者に三面の国(三角)が含まれていないことを示すために繰り返すことができますが、正方形を置き換えると、隣の国がfourcoloursすべてを使用している可能性があるため、証明手順が失敗するため、正方形でテクニックを試してみると破壊されます。 これが起こったら、それは五角形のために動作しません明らかになり、というように。
六色定理
同様の手法を適用して、六色定理が真であることを示すことができる。 まず、六つの色で着色できるマップがないと仮定します。 いくつかのマップは七色で着色することができるので、これらのいずれかを選択する(最小限の犯罪者)、七色未満で着色することが可能であることを示
五隣接定理の証明から、任意のマップがsixcoloursで着色することができることを示すために、最小限の犯罪的な考えを使用してプロセスすることが可能である!
領域から結び目、ネットワーク、トポロジーへ
1879年、アルフレッド-ケンペ(1849年-1922年)は、上記のような技術を用いて、”五つの隣人特性”から始まり、”ケンペ鎖”の方法として知られる手順を開発し、四色定理の証明を見つけた。 彼はこの証明をAmerican Journal of Mathematicsに発表しました。 パーシー-ヒーウッド(1861年-1955年)がケンペが使用していた証明方法に重要な誤りがあることを示す前に、彼の証明は十年のために立っていた。


Alfred Kempe(1849-1922)、PeterGuthrie Tait(1831-1901)Percy Heawood(1861-1955)
1880年に数学物理学者のp.g.tait(1831-1901)がこの問題の解決策を提供しました。 独立して、Taitは、偶数の境界線がすべての点で出会うマップを2色で着色できることを確立していましたが、この結果はKempeの論文で以前に現れました。
1876-77年の間、Taitは彼の研究と結び目の分類でよく知られるようになりました。 その時、原子の構造に関する異なる理論。 ウィリアム-トンプソン(William Thompson,Lord Kelvin,1824-1907)は、ドイツの物理学者ヘルマン-フォン-ヘルムホルツ(Hermann von Helmholtz,1821-1894)の実験に触発されて、原子はエーテルの管で結ばれているという仮説を提案した。 ケルビンの”vortex原子”の理論は約二十年間真剣に取られ、それは結び目の分類を引き受けるためにTaitを刺激した。 Tait,Thomsonand James Clark Maxwell(1831-1879)は、彼らの研究の間に多くの位相的アイデアを発明しました。 しかし、ケルビンの理論は基本的に物理学者はテイトの研究に興味を失った。


ヘルマン・フォン・ヘルムホルツ(1821-1879)、ケルビン卿(1824-1907)そして、ジェームズ*クラーク*マクスウェル(1831-1879)

Taitは、コードのasingle閉ループが可能な方法で始ま結ばれます。 彼は最初にsystematicmethodを持っていなかったし、asingle閉ループを取って、itcould結び目の方法を実験することによって直感的な方法で始めました。 もちろん、コードは開いていなければなりませんでした(ashoelaceのように)その後、結ばれ、結合されました。 あなたが結び目の周りのコードに従うと、”オーバーアンダー”交差が交互になることに注意してください。彼はその後、二つのループとそれらを一緒に結ぶことができる方法を実験するようになりました。 ここでは、単一のループのためのsixcrossingsまでのノットが示されています。
テイトの研究の成果の一つは、彼のハミルトニアングラフ予想でした。
マップは、球上に描かれた多面体とみなされ、平面に投影することができます。 テイトは任意の立方多面体写像がハミルトニアン環を持つことを提案した。 Taitの方法は、グラフのエッジに焦点を当て、彼はハミルトニアンサイクルが四色ofaマップを生成することができることを示した。 William Tutte(1917-2002)がTaitの予想に対する最初の反例を見つけたのは1946年までではありませんでした。
Taitと結び目との関係
Taitinitiは1880年にsnarksの研究を開始し、fourcolourの定理はsnark isplanarがないという声明と同等であることを証明しました。 平面グラフは、平面内に描くことができるグラフですエッジが交差することはありません。 非平面グラフのTaitのアイデアは、結び目とハミルトニアン経路の彼の研究から来ているかのように見えます。
最初に知られているスナークは1898年に発見されたPetersenグラフであり、数学者はこれらの種類のグラフの多くを狩り始めましたが、別のスナークが発見されたのは1946年までではありませんでした。
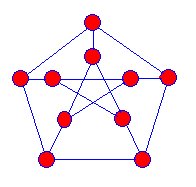 |
スナークは三つの投影です次元グラフを平面上に配置します。 青いエッジが他のエッジと交差するように見える頂点はありません。 Snarksは次のプロパティを持ちます。
|
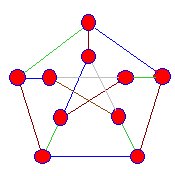 |
このスナークの頂点を満たすエッジは青、緑、茶色に着色されていますが、常にこのプロセスを継続することはできません。 |
ジュリアス*ピーターソン(1839-1910)
theSnarkの狩猟は詩ですルイス-キャロルとマーティン-ガードナーによって書かれたこれらのグラフは、非常にとらえどころのないものだったので、snarksと命名されました。
問題を変換し、新しい方法を見つける。
1890年にケンペの証明法に大きな欠陥を発見したが、四色定理を証明することはできなかったが、彼は大きなブレークスルーを作り、すべての地図が五色で着色できることを最終的に証明した。
Heawoodはこの問題に多くの重要な貢献をし、注意の焦点を地図の領域からそれらの間の境界に移しました。 1898年までに、彼は各地域の周りの数が3で割り切れるならば、地域は四つの色で着色することができることを証明していた。
コーシーのオイラーの公式の証明には、多面体の任意のネットは、三角形の面に辺を追加することによって三角形にすることができるという考えも含まれていた。 彼はその後、彼はオイラーの公式は、各ステップで維持することができることを示し、エッジを一つずつ削除するprocedurewherebyを開発しました。
コーシーのオイラーの公式の証明
コーシーの1813年のオイラーの公式の証明は、平面ネットを得るための多面体の射影の考えから始まりました。 彼はさらに(a)任意のネットを三角測量することができ、オイラーの公式の彼の証明(b)は、当時受け入れられました。
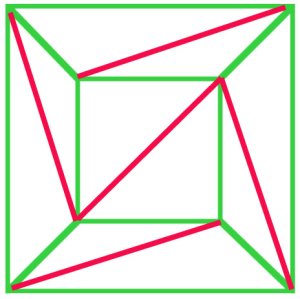 (a)
|
In principle, every polygonal net can be triangulated. In thisnet of a cube (a), $f + v – e$ is $10 + 8 – 17 = 1$, and Euler’sformula still holds. |
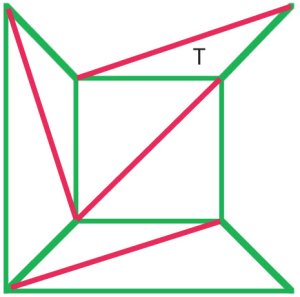 (b)
|
コーシーの引数は、図(a)から外部エッジを一つずつ削除し、図(b)のようにステージに達したときオイラーの公式。 19世紀初頭の多くの数学者は、この手順はすべての多面体に対するオイラーの公式の証明を示したことに同意した。 |
1900年までに、数学者は平面グラフが双対性の強力な概念を使用して任意のマップから構 双対では、領域は頂点で表され、2つの頂点は領域が隣接している場合は辺で結合されます。 これらのグラフでは、FourColour予想は、グラフの頂点が4色で着色できるかどうかを尋ね、隣接する2つの頂点が同じ色ではないかどうかを尋ねます。
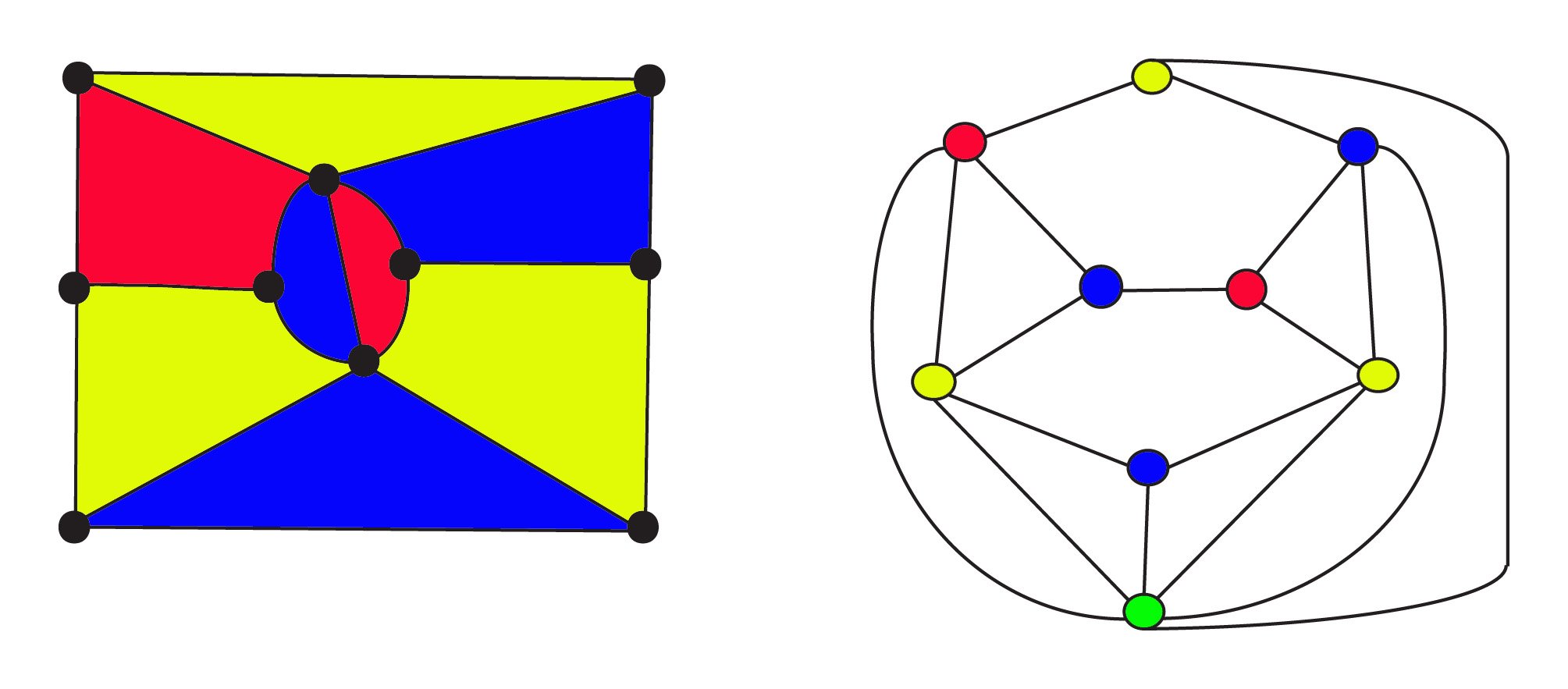
の3色の地図の左側は$8$の地域で$10$頂点と$17$いですね。 そのデュアルグラフtherightは$9$-地域$9$頂点と$17$縁theverticesている色と同じ分野をまとめたものです。 グラフの下部にあるgreenvertexは、マップの無限のexternalareaを表します。 元のマップとその二重は、ネットワークnetworks f+v-e=1networksまたはnetworks\text{regions}+\text{vertices}-\text{edges}=1.のオイラーの公式に従います。 双対関係は対称:双対の双対は元のグラフになり、領域と頂点が交換されます。
二十世紀の前半の間に、mathematiciansfocusedは、それらの特定の特性を調査するために、識別し、分類することができる特別なケースに複雑なマップを還元するために、この種の技術を変更することに焦点を当て、テストすることができるマップ構成の最小限のセットのアイデアを開発しました。
最初の例では、セットには9,000人近くのメンバーが含まれていると考えられていたため、数学者はコンピュータ技術に頼って、それらのテストを行うことができるアルゴリズムを記述した。 アルゴリズムは、最小セットのメンバーの数を減らすために、他の技術と一緒にチェーンのKempeのオリジナルのアイデアの修正版を使用しました。
ジョン-コッホと協力して還元性の問題について研究した後、1976年にイリノイ大学でケネス-アプランド-ヴォルフガング-ハケンは最終的にテスト問題を1,936個の構成を持つ無相対性理論に還元し、四色予想に対する完全な解を達成した。 マップの還元性を一つずつチェックするこの問題は、異なるプログラムと異なるコンピュータでダブルチェックされました。 彼らの証明は、5色を必要とする地域の最小数を持つ少なくとも1つの地図が存在できないことを示しました。最初の証明以来、より効率的なアルゴリズムが4-彩色写像のために発見され、1994年までに633個に減少していた。
コンピュータ上で行われた’証明’は適切な証明ですか?証明はコンピュータの助けを借りて行われたので、すぐに抗議がありました。 多くの数学者や哲学者は、その証明は正当ではなかったということです。 いくつかの人は、証明は機械ではなく人々によって”証明”されるべきであると言いましたが、他の人は、より実用的な心の両方のアルゴリズムの信頼性としかし、数学者によって書かれた証明の多くは、欠陥があることが判明しているため、信頼性に関する議論は空のようです。意見が表明されたものは何でも、状況はまだ今日continuestoday証拠の性質について深刻な議論を生み出しました。
教育的なノートの場合:
この記事の上部にあるノートタブを使用するか、ここをクリックしてください。
Notes
- これとこのセクションで見つかった他の手順の詳細は、Robin Wilsonの本Four Colours Suffleで見ることができます。
- 結び目は左利きまたは右利きにすることができ、今日は化学、薬学、生物学および物理学におけるこの特性の重要な応用。 ウィリアム・ローワン・ハミルトン(William Rowan Hamilton、1805年-1865年)にちなんで命名された。 グラフ内のハミルトニアン経路は、それぞれの頂点を正確に一度訪問する。 ハミルトニアン-サイクル(Hamiltonian cycle、またはcircuit)とは、各頂点を正確に一度訪れ、その頂点に戻るapathである。Imre Lakatosによる本、Proofs and Refutationsには、コーシーの手順(6-12ページ)に対する議論と批判があり、オイラーの定理の話についてはさらに多くのものがあります。
- 双対性の考え方は、16世紀と17世紀に射影幾何学の発展に伴って生じた。 PascalやDesarguesのような数学者は、特定の幾何学的構成の記述の中で「点」と「線」を交換することによって新しい定理が見つかることを発見しました。 一例は正則多面体であり、一方の頂点は他方の面に対応する。 したがって、四面体の双対は別の四面体であり、立方体の双対は八面体です。 双対の双対は元の多面体。
四つの色に関する非常に人気のある、読みやすい本は次のとおりです。
Wilson,R.(2003)
四つの色で十分です。
ロンドン。 ペンギンの本。
より詳細で技術的な歴史については、標準参照本は次のとおりです。
Biggs,N.;Lloyd,E.&Wilson,R.(1986)(1998)
Graph Theory,1736-1936
Oxford. オックスフォード大学出版局。これは、より最近の基礎と哲学で、最新のものに私たちをもたらします。フリッチュ、Rとフリッチュ、G(2000)
四色定理:歴史、位相的基礎、および証明のアイデア
ニューヨーク。 シュプリンガー=ヴェルラグ
イングランド-ハーロウ出身。 アディソン-ウェズリー-ロングマン
一般的な歴史書はほとんど主題について多くを持っていないが、カッツの”Computers and Applications”と呼ばれる最後の章はグラフ理論に関するものであり、四色定理が言及されている。
Polya G.どのように解決するにはそれ。
これは問題解決に関する古典的な本です。 それが最初に1950年代に登場し、それはまだ簡単に利用可能であるので、この本の多くの版がありました。 不思議なことに、最近の版は、サブタイトル”数学的方法の新しい側面”を与えられています。
Lakatos,I.(1976)Proofs andRefutations:The Logic of Mathematical Discovery.
ケンブリッジ C.U.P.
これは、1970年代の問題解決と調査の研究につながったもう一つの重要な本です。 それはオイラーの公式の証明についての教師と学生のグループの間のaclassroomの議論として始まり、十九世紀の数学者そして科学者によって実際に論議された考え、異議および可能性によって及ぶ。 それは、教育と学習問題の解決と数学的方法と証明についての最も重要な問題のいくつかを提起します。
関連する参考文献
私はしばらくの間、文字列ゲームに関する小さな本を持っていました。 学校では”猫のゆりかご”と呼ばれていて、私たちが遊んでいました。
最近、フランスのジャーナルは、文字列の数字の’algebra’に関する論文を発表しました! アマゾンに行けば、アン-スウェインとマイケル-テイラーによる”Finger Strings:A Book of Cats Cradles andString Figures”という本がフロリス-ブックスから2008年に出版されている。 色付きで説明されているいくつかの80の数字がありますdiagrams.It’sの螺旋綴じ、従ってそれはtheinstructionsに続く間、開いたとどまります。 また、文字列ループのカップルが付属しています!
結び目の専門家のために、結び目のAshleyBookは、結び目とその用途の異なる種類のthehundredに興味のある人のための古典です。 Amazonは異なる価格で利用可能な様々なエディション。
Webリンク
多くの人々やトピックへの一般的な概要とリンクについては、theMacTutorのウェブサイトは
そしてもちろん、すべての異なる数学的側面をindeveloping関係者のMacTutorの伝記は、mactutorの伝記インデックスで見つけることができます。4色の定理と3つの証明。
4色の定理と3つの証明。
数学的に永続的なために、次のウェブサイトは、問題を解決するための新しいアルゴリズムを構築し、コンピュータへの依存を減らすために結びつけるという問題を解決するための興味深い新しいアプローチを持っています。http://www.emu.edu.tr/~cahit/the%20four%20color%20theorem%20—%20three%20proofs.htm
グラフ理論のために、Wikipediaは良い概要を与え、あなたは本当に技術的なものをskipすることができます。 それは現代の種類を示しています数学のこの分野の応用。 GraphColouringに移動してFour Colour Theoremをクリックすると、より多くの情報が見つかります。
結び目理論の興味深い、そしてあまり技術的ではない歴史-ケルビンの物理学からのアイデアが原子理論にどのように戻るか今日。
数学の教師の協会は、ケルトKnotdesignのポスターを持っています。 彼らのウェブサイトに移動し、アルファベットを参照してくださいリソースのリスト。
結び目アトラスの結び目についてのすべてを見つけてください! あなたはanexpertではない場合-ちょうどデータベースの多様性と複雑さを楽しむ”wikiの精神”
より芸術的でカラフルな-しかし、劣らず数学的なTheknotプロットサイト
元のものとhistoricaldetailのいくつかをしたい人のために上の結び目理論の歴史に行きます:
