Le Théorème des Quatre Couleurs
La Conjecture des Quatre Couleurs a été énoncée pour la première fois il y a un peu plus de 150 ans et a finalement été prouvée de manière concluante en 1976. C’est un exemple remarquable de la façon dont les idées anciennes se combinent avec de nouvelles découvertes et techniques dans différents domaines des mathématiques pour fournir de nouvelles approches à un problème. C’est aussi un exemple de la façon dont un problème apparemment simple a été pensé pour être « résolu » mais est ensuite devenu plus complexe, et c’est le premier exemple spectaculaire où un ordinateur a été impliqué dans la preuve d’un théorème mathématique.
Au début
La conjecture selon laquelle n’importe quelle carte pourrait être colorée en utilisant seulement quatre couleurs est apparue pour la première fois dans une lettre d’Auguste De Morgan (1806-1871), premier professeur de mathématiques au new University College de Londres, à son ami William RowanHamilton (1805-1865) le célèbre mathématicien irlandais en 1852. Il avait été suggéré à De Morgan par l’un de ses étudiants, FrederikGuthrie, au nom de son frère aîné Francis (qui devint plus tard professeur de mathématiques à l’Université du Cap).


Augustus De Morgan (1807-1871) Etwilliam Rowan Hamilton (1805-1865)
Le problème, si simplement décrit , mais si incroyablement difficilepour prouver, a attiré l’imagination de nombreux mathématiciens à l’époque. À la fin des années 1860, De Morgan emmena même le problème et sa preuve en Amérique où, entre autres, Benjamin Peirce (1809-1880), mathématicien et astronome célèbre, s’y intéressa pour développer ses méthodes logiques.
De Morgan a utilisé le fait que sur une carte à quatre régions, chacune touchant les trois autres, l’une d’elles est complètement fermée par les autres. Comme il ne pouvait pas trouver un moyen de le prouver, il l’utilisa comme un axiome, la base de sa preuve.
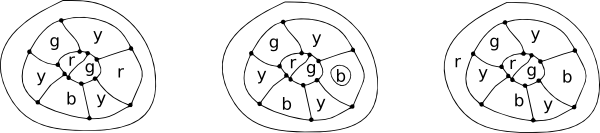
Une copie de l’original de De Morgan dans sa lettre à Hamilton et une simple carte en quatre couleurs.
En 1878, Arthur Cayley (1821-1895), lors d’une réunion de la LondonMathematical Society, a demandé si quelqu’un avait trouvé une solution à la question initiale dede Morgan, mais bien qu’il y ait eu un certain intérêt, personne n’avait fait de progrès significatifs. Cayley devint intéressé par le problème et, en 1879, publia un court document sur la coloration des cartes où il expliqua certaines des difficultés à tenter une preuve et apporta d’importantes contributions à la façon dont le problème était abordé. Sa question: « si une carte particulière est déjà colorée avec quatre couleurs et que nous ajoutons une autre zone, pouvons-nous toujours garder la même coloration? » a commencé une autre ligne d’enquête qui a conduit à l’application de l’induction mathématique au problème.

Arthur Cayley (1821-1895)
Arthur Cayley a montré que si quatre couleurs avaient déjà été utilisées pour colorer une carte et qu’une nouvelle région était ajoutée, il n’était pas toujours possible de conserver la couleur d’origine.
Ci-dessus, les quatre couleurs ont été utilisées sur la carte originale, et une nouvelle région est dessinée pour l’entourer. Dans ce cas, une région rouge est changée en bleu, de sorte que le rouge peut être utilisé sur la nouvelle région environnante.
Cayley a également observé qu’il était possible de résoudre une version du problème en limitant la façon dont les limites se rencontraient. Par exemple, les cartes où seulement trois pays se sont rencontrés ont trois bords qui se rencontrent à avertex. Celles-ci sont appelées « cartes cubiques », et les cartes utilisées dans la discussion suivante sont toutes des cartes cubiques. De plus, si une carte peut être colorée de quatre couleurs, seules trois couleurs apparaîtront à la frontière.
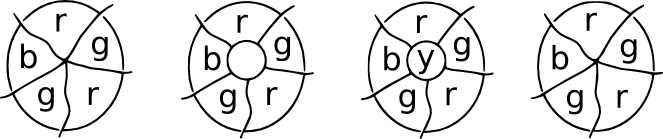
La démonstration du patch. Imaginez queà un endroit sur une carte, un certain nombre de pays se rencontrent en un point. Maintenant, placez un patch sur le point de rencontre, et tous les nouveaux points de rencontre auront trois frontières qui en émaneront. Ce sont des cartes cubiques, et une quatrième couleur peut être utilisée pour la région centrale. En retirant le patch, nous pouvons revenir à la coloration d’origine.
Quelques techniques anciennes, de nouvelles conditions et plus de problèmes!
Afin de suivre l’évolution du problème, nous devons examiner brièvement certaines des idées, procédures et techniques que les mathématiciens ont développées dans leurs tentatives pour le résoudre.
Les cinq seules Conjectures voisines
‘Si vous ne pouvez pas résoudre un problème aparticulaire, trouvez-en un plus facile que vous pouvez résoudre. » (Polya. Comment le résoudre)
‘Chaque carte a au moins un pays avec cinq voisins ou moins.’
Imaginez une carte d’une île entourée par la mer. Dans la couleur des pays de l’île, nous comptons la mer comme une seule région. Certains pays peuvent n’avoir que deux frontières (un digon), quelque trois (comme dans un triangle), quatre (un carré) et cinq (apentagon) ou plus.
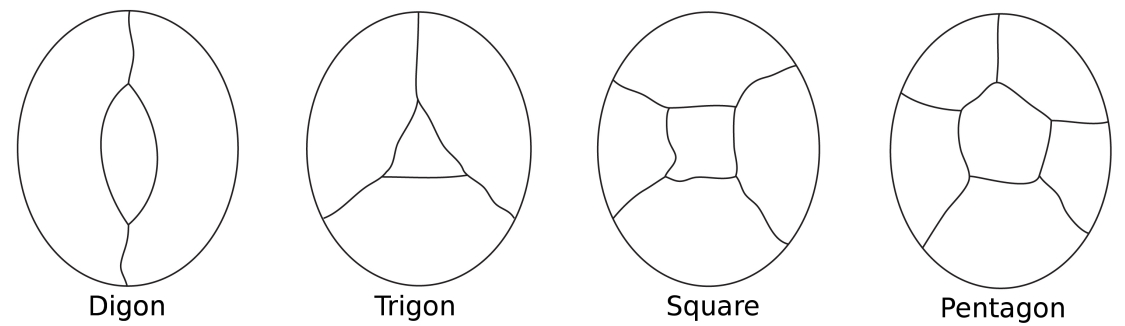
Les configurations les plus simples possibles pour entourer une région centrale.
Notez que dans toutes ces configurations, chaque nœud n’a que trois bords.
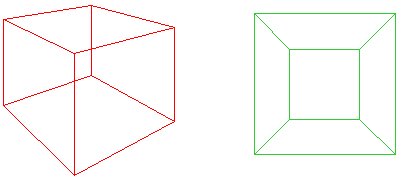
En 1813, la formule d’Euler pour les polyèdres a été adaptée en deux dimensions par Augustin Cauchy (1759-1857) en jetant le polyèdre sur un plan formant ainsi le réseau du solide. De cette façon, la formule est devenueff + v -e = 1 bec, Carauchy ne comptait pas la région « extérieure » du filet.

Augustin Cauchy (1759-1857)
Imaginez écraser le cube rouge sur un plan afin que sa base soit ouverte pour former la bordure extérieure du filet vert. L’idée de Cauchy était de découper une face du cube, de sorte que pour un polygone plan, $f + v-e = 1$. Alternativement, si l' »extérieur » du filet est considéré comme une face avec infinitearea, alors nous avons toujoursff + v-e = 2
Nous pouvons supposer qu’il y a au moins trois lignes de bordure (arêtes) émergeant de chaque point de rencontre (sommets).
La preuve que la carte comporte au moins un pays entouré de cinq voisins ou moins procède par contradiction. Si cela conduit à une absurdité, nous avons une preuve.
Maintenant, mettez ces valeurs dans la formule d’Euler:ff + v-e = 2 and et nous avons $$1/3(e) + 2/3(e)-e which qui est nul!
C’est l’absurdité, donc notre hypothèse initiale était fausse.Cela signifie qu’il doit y avoir au moins un pays avec cinq voisins ou moins!
Criminels minimes!
Une autre façon de résoudre le problème des quatre couleurs est de supposer qu’il est faux et de voir où cela mène. Supposons qu’il y ait des cartes qui ont besoin de cinq couleurs ou plus, et nous choisissons les cartes avec le plus petit nombre possible de pays. Ces cartes sont appelées contre-exemples minimaux oudes criminels minimaux!
Cela signifie donc qu’un criminel minimal ne peut pas être coloré avec quatre couleurs, mais n’importe quelle carte avec moins de pays peut être colorée avec quatre couleurs. Si nous pouvons montrer que les criminels minimes ne peuvent pas exister, alors nous pourrons peut-être faire des progrès.
Par exemple, nous pouvons montrer qu’un criminel minimal ne peut pas contenir un digon.
De la carte originale, enlevez une limite du digon, et nous obtenons une nouvelle carte avec moins de pays. Cette carte peut être coloriée en quatre couleurs (selon notre hypothèse). Nous colorions ensuite cette nouvelle carte, (nous n’avons besoin que de deux couleurs). Maintenant, remplacez la bordure que nous avons supprimée et coloriez la carte. Nous avons utilisé trois couleurs, et comme il reste encore une couleur disponible, cela montre que notre carte peut être colorée avec quatre couleurs. Mais c’est contre notre hypothèse, donc un criminel minimal ne peut pascontenir un digon.
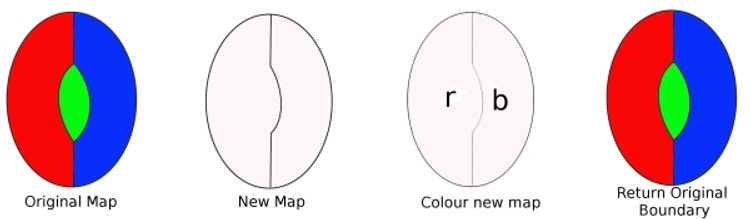
Pour montrer qu’un Criminalcannot Minimal contient une région à deux bords (un digon). Supposons qu’il y ait un criminel minimal qui contient un digon. Supprimer un bord signifiela carte contient moins de régions. Cette nouvelle carte peut donc être coloriée en quatre couleurs. Remplacez maintenant le bord perdu. Puisque seulement deux couleurs étaient nécessaires auparavant, le remplacement du bord signifie que nous pouvons utiliser une troisième couleur, et avoir encore une quatrième couleur à utiliser. Ainsi, un minimalcriminel peut être coloré avec quatre couleurs. Par conséquent, un minimalcriminal ne peut pas contenir de digon.
Cette procédure peut être répétée pour montrer qu’un criminel minimal ne contient pas un pays à trois faces (un trigon), mais il se décompose lorsque nous essayons la technique sur un carré, car lorsque nous remplaçons le carré, les pays à côté peuvent bien utiliser les quatre couleurs, donc la procédure de preuve échoue. Une fois que cela s’est produit, il devient évident que cela ne fonctionnera pas pour les pentagones, etc.
Le Théorème des six couleurs
Une technique similaire peut être appliquée pour montrer que le théorème des six couleurs est vrai. Tout d’abord, nous supposons qu’il n’y a pas de cartes qui peuvent être colorées avec six couleurs. Certaines cartes peuvent être colorées avec sept couleurs, donc en sélectionnant l’une d’elles (un criminel minimal), si nous pouvons montrer qu’il est possible de la colorer avec moins de sept couleurs, nous avons atteint notre objectif.
À partir de la preuve du théorème des cinq voisins, il est possible de procéder en utilisant l’idée criminelle minimale pour montrer que n’importe quelle carte peut être colorée avec six couleurs!
Des régions aux Nœuds, aux Réseaux et à la topologie
En 1879, Alfred Kempe (1849-1922), utilisant des techniques similaires à celles décrites ci-dessus, est parti de la « propriété des cinq voisins » et a développé une procédure connue sous le nom de méthode des « chaînes de Kempe » pour trouver une preuve du Théorème des quatre couleurs. Il a publié cette preuve dansl’American Journal of Mathematics. Il a trouvé deux versions plus simples qui ont été publiées l’année suivante, et sa preuve a duré dix ans avant que Percy Heawood (1861-1955) ne montre qu’il y avait une erreur importante dans la méthode de preuve utilisée par Kempe.


Alfred Kempe (1849-1922), PeterGuthrie Tait ( 1831-1901) et Percy Heawood (1861-1955)
En 1880 P.G. Tait (1831-1901) un physicien mathématique, offritune solution au problème. Indépendamment, Tait avait établi que les cartes où un nombre pair de lignes de démarcation se rencontrent en chaque point pouvaient être colorées de deux couleurs, bien que ce résultat soit apparu plus tôt dans les papiers de Kempe.
En 1876-77, Tait est devenu bien connu pour son étude et sa classification des nœuds. A cette époque, il y avait un certain nombre dedifférentes théories sur la structure des atomes. William Thompson (Plus tard, Lord Kelvin 1824-1907) inspiré par les expériences du physicien allemand Hermann von Helmholtz (1821-1894) a proposé une théorie selon laquelle les atomes étaient des tubes d’éther noués. La théorie de Kelvin des « atomes de vortex » a été prise au sérieux pendant une vingtaine d’années et a inspiré Tait à entreprendre une classification des nœuds. Tait, Thomsonet James Clark Maxwell (1831-1879) ont inventé de nombreuses idées topologiques au cours de leurs études. Cependant, la théorie de Kelvin était fondamentalementmis en place et les physiciens ont perdu tout intérêt pour le travail de Tait.


Hermann von Helmholtz (1821-1879), Lord Kelvin ( 1824-1907) et James Clark Maxwell (1831-1879)

Tait a commencé par les façons dont une boucle fermée unique de cordon pouvait être nouée. Il n’avait pas de méthode systématique au début, et a commencé de manière intuitive en prenant une boucle fermée unique et en expérimentant les façons dont elle pouvait être nouée. Bien sûr, le cordon devait être ouvert (comme ashoelace) puis noué et joint. Notez que si vous suivez le cordon autour du nœud, les croisements « over-under » alterneront.Il a ensuite expérimenté deux boucles et les façons dont elles pouvaient être nouées ensemble. Voici les nœuds avec jusqu’à six croisements pour une seule boucle.
L’un des résultats de l’étude de Tait était sa conjecture de graphe hamiltonien.
Une carte est considérée comme un polyèdre dessiné sur une sphère, et elle peut ensuite être projetée sur un plan. Tait a proposé que toute carte polyèdre cubique ait un cycle hamiltonien. La méthode de Tait s’est concentrée sur les arêtes du graphe etil a montré qu’un cycle hamiltonien pouvait produire une carte ofa à quatre couleurs. Ce n’est qu’en 1946 que William Tutte (1917-2002) a trouvé le premier contre-exemple à la conjecture de Tait.
Tait et la connexion avec les nœuds
Taitinitia l’étude des snarks en 1880, lorsqu’il prouva que le théorème des quatre couleurs était équivalent à l’affirmation selon laquelle aucun snark n’est planaire. Un graphe planaire est un graphe qui peut être dessiné dans le plan sans croisements d’arêtes. Il semble que l’idée de Tait des graphes non planaires soit venue de son étude des nœuds et des chemins hamiltoniens.
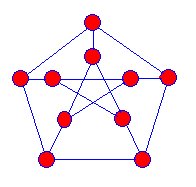
Le premier snark connu a été le graphe de Petersen découvert en 1898, et les mathématiciens ont commencé à rechercher davantage de ces types de graphes, mais ce n’est qu’en 1946 qu’un autre snark a été trouvé.
|
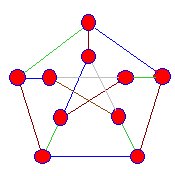
Les snarks sont des projections de graphes tridimensionnels sur l’avion. Il n’y a pas de sommets où les bords bleus semblent se croiser les uns les autres. Les snarks ont les propriétés suivantes :
|
|
Les arêtes rencontrant les sommets de ce snark sont colorées en bleu, vert et marron, mais nous arrivons toujours à un stade où ce processus ne peut pas être poursuivi. |
Julius Peterson (1839-1910)
La chasse of theSnark est un poème écrit par Lewis Carroll, et Martin Gardn a appelé ces graphiques Snarks, parce qu’ils étaient si insaisissables.
Transformer le problème et trouver de nouvelles méthodes.
Bien que Heawood ait trouvé le défaut majeur dans la méthode de preuve de Kempe en 1890, il n’a pas pu continuer à prouver le théorème des quatre couleurs, mais il a fait une percée significative et a prouvé de manière concluante que toutes les cartes pouvaient être coloriées avec cinq couleurs.
Heawood a apporté de nombreuses contributions importantes au problème, déplaçant l’attention des zones d’une carte vers les frontières entre elles. En 1898, il avait prouvé que si le nombre d’arêtes autour de chaque région était divisible par 3, les régions pouvaient être colorées avec quatre couleurs.
La preuve de Cauchy de la formule d’Euler incluait également l’idée que tout réseau d’un polyèdre peut être triangulé en ajoutant des arêtes pour transformer des faces non triangulaires en triangles. Il a ensuite développé une procédure en supprimant les bords un par un, montrant que la formule d’Euler pouvait être maintenue à chaque étape.
La preuve de Cauchy de la Formule d’Euler
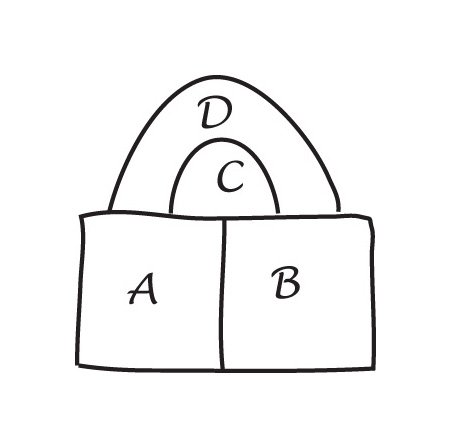
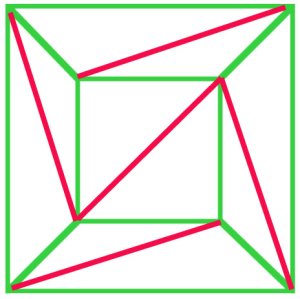
La preuve de Cauchy de 1813 de la Formule d’Euler a commencé avec l’idée d’une aprojection d’un polyèdre pour obtenir un filet plan. Il a ensuite démontré (a) que tout filet pouvait être triangulé, et sa preuve (b) de la formule d’Euler a été acceptée à l’époque.
 (a)
|
In principle, every polygonal net can be triangulated. In thisnet of a cube (a), $f + v – e$ is $10 + 8 – 17 = 1$, and Euler’sformula still holds. |
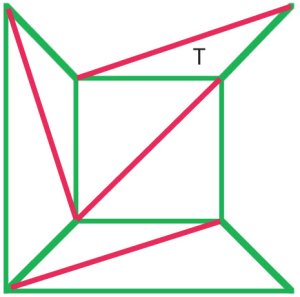 (b)
|
L’argument de Cauchy était de supprimer les bords externes du diagramme (a) un par un, et lorsqu’il atteignait un stade comme dans le diagramme (b) supprimé le triangle entier T, préservant ainsi la formule d’Euler. De nombreux mathématiciens du début du XIXe siècle ont convenu que cette procédure démontrait une preuve de la formule d’Euler pour tous les polyèdres. |
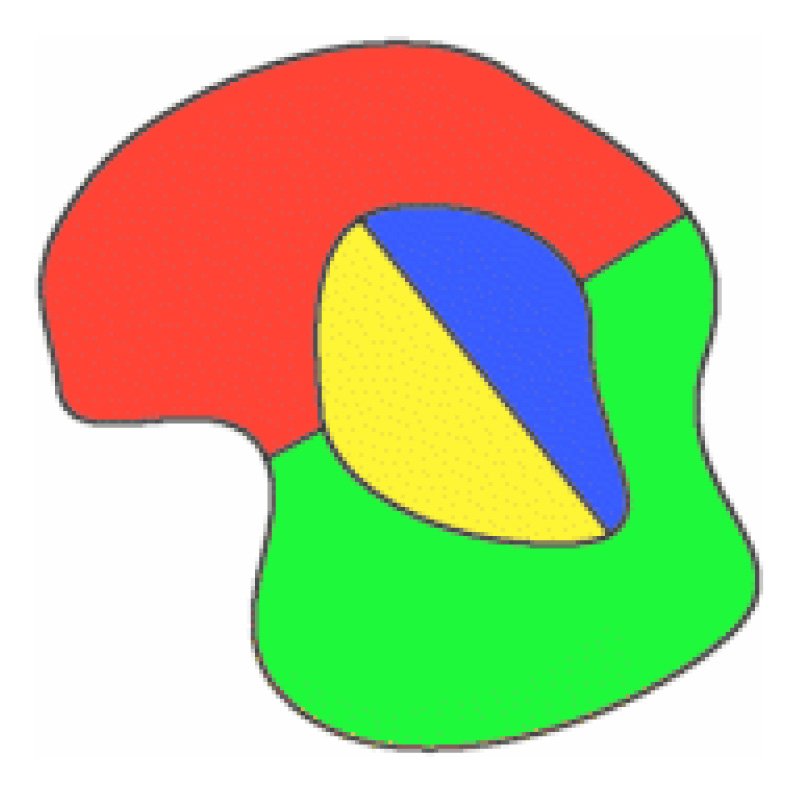
En 1900, les mathématiciens savaient qu’un graphe planaire peut être construit à partir de n’importe quelle carte en utilisant le puissant concept de dualité. Dans le dual, les régions sont représentées par des sommets et deux sommets sont joints par une arête si les régions sont adjacentes. Dans ces graphes, la conjecture des quatre couleurs demande maintenant si les sommets du graphe peuvent être colorés avec 4 couleurs de sorte qu’il n’y ait pas deux sommets adjacents de la même couleur.
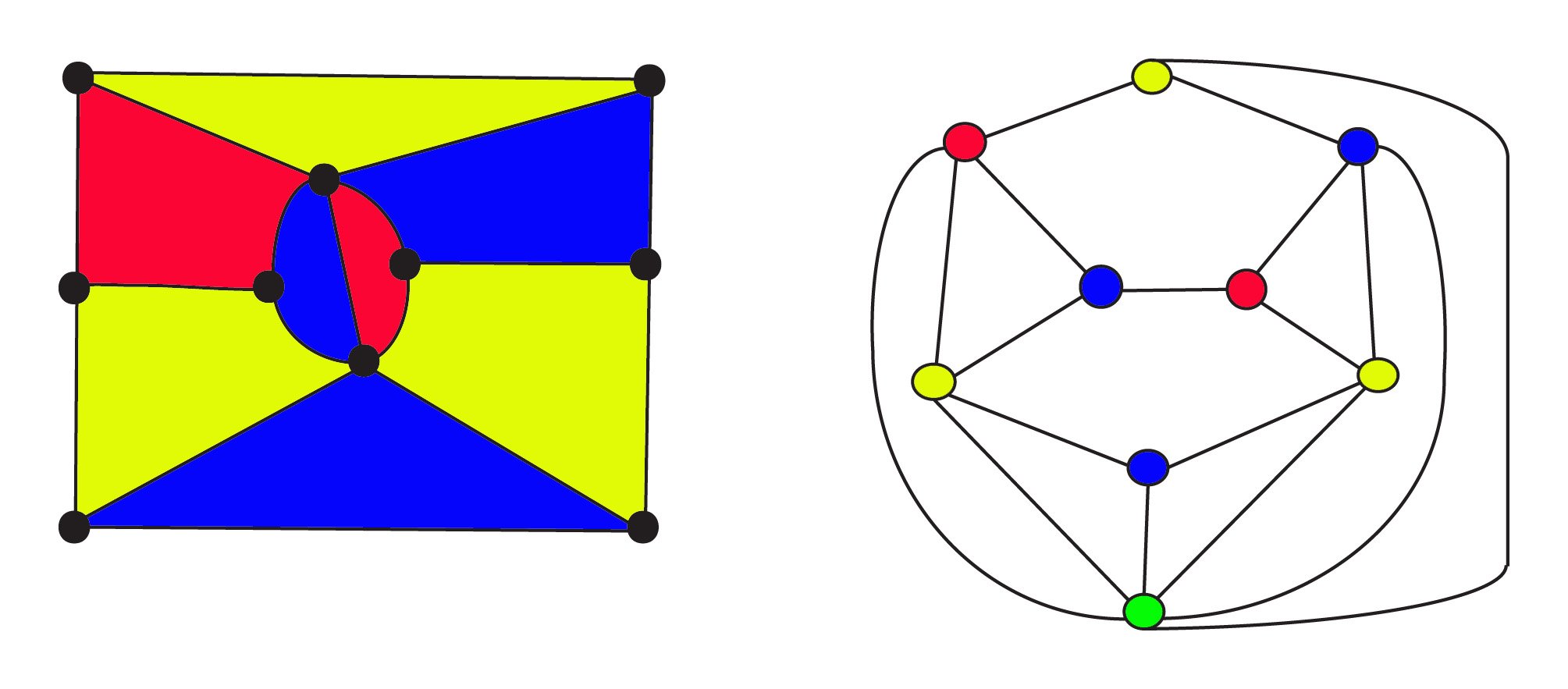
Le 3 de couleur de la carte sur la gauche a$8$ les régions de $10$ sommets et $17$ bords. Son graphe dual droit a $9$ régions $9$ sommets et $17$ bords où thevertices sont colorés de la même que les zones de la carte. Le vertvertex en bas du graphique représente la zone externe infinie de la carte. La carte d’origine et sa double obéissent toutes deux à la formule d’Euler pour les réseauxff + v-e = 1 or ou,\\text{regions} +\text{sommets} – \text{arêtes} = 1$. La relation de dualité estsymétrique: le dual du dual sera le graphe d’origine, où les régions et les sommets sont échangés.
Au cours de la première moitié du XXe siècle, les mathématiciens se sont concentrés sur la modification de ces types de techniques pour réduire les cartes compliquées à des cas particuliers qui pouvaient être identifiés et classifiés, pour étudier leurs propriétés particulières et développer l’idée d’un ensemble minimal de configurations cartographiques pouvant être testées.
Dans un premier temps, on pensait que l’ensemble contenait près de 9 000 membres, ce qui était une tâche énorme, et les mathématiciens se sont donc tournés vers des techniques informatiques pour écrire des algorithmes capables de les tester. Les algorithmes ont utilisé des versions modifiées de l’idée originale de chaînes de Kempe avec d’autres techniques pour réduire le nombre de membres de l’ensemble minimal.
Après avoir collaboré avec John Koch sur le problème de la réductibilité, en 1976 à l’Université de l’Illinois, Kenneth Appeland Wolfgang Haken a finalement réduit le problème de test à un ensemble non modifiable avec 1936 configurations, et une solution complète à la conjecture des Quatre couleurs a été obtenue. Ce problème de vérification de la réductibilité des cartes une par une a été vérifié avec différents programmes et différents ordinateurs. Leur preuve a montré qu’au moins une carte avec le plus petit nombre possible de régions nécessitant cinq couleurs ne peut exister.
Depuis la première preuve, des algorithmes plus efficaces ont été trouvés pour les cartes à 4 couleurs et en 1994, l’ensemble inévitable de configurations avait été réduit à 633.
Une « Preuve » faite sur un ordinateur est-elle une Preuve appropriée?
Comme la preuve a été faite à l’aide d’un ordinateur, il y a eu un tollé immédiat. De nombreux mathématiciens et philosophes ont prétenduque la preuve n’était pas légitime. Certains ont dit que les preuves devaient être « prouvées » par des personnes, et non par des machines, tandis que d’autres, d’un esprit plus pratique, remettaient en question la fiabilité des algorithmes et la capacité des machines à les exécuter sans erreur.Cependant, bon nombre des preuves écrites par des mathématiciens ont étérouvé être erronées, de sorte que l’argument sur la fiabilité semble vide.Quelles que soient les opinions exprimées, la situation a donné lieu à de sérieuses discussions sur la nature de la preuve qui se poursuivent encore aujourd’hui.
Pour les notes pédagogiques :
Utilisez l’onglet notes en haut de cet article ou cliquez ici.
Notes
- Plus de détails sur cette procédure et les autres que l’on trouve dans cette section peuvent être vus dans le livre Four Colours Suffise de Robin Wilson.
- Les nœuds peuvent être gauchers ou droitiers, et aujourd’hui il y aapplications importantes de cette propriété en chimie, pharmacie, biologie et physique. (Voir Notes pédagogiques)
- Nommé d’après William Rowan Hamilton (1805-1865). Un chemin hamiltonien dans un graphe visitechaque sommet exactement une fois. Un cycle hamiltonien (ou circuit) est un chemin qui visite chaque sommet exactement une fois et revient au sommet de départ.(Voir Notes pédagogiques)
- Le livre d’Imre Lakatos, Preuves et Réfutations a une discussion et une critique de la procédure de Cauchy (pages 6 – 12), et beaucoup plus sur l’histoire du Théorème d’Euler.
- L’idée de dualité est née aux XVIe et XVIIe siècles avec les développements en géométrie projective. Des mathématiciens comme Pascal Etdesargues ont découvert que de nouveaux théorèmes pouvaient être trouvés en échangeant les termes « point » et « ligne » dans les descriptions de certaines configurations géométriques. Un exemple est dans les polyèdres réguliers, où lesvertices de l’un correspondent aux faces de l’autre. Ainsi, le dual d’un tétraèdre est un autre tétraèdre, et le dual d’un cube est un octaèdre. Le dual du dual est l’originalpolyèdre.
Le meilleur livre populaire et facile à lire sur le thème des quatre couleurs est:
Wilson, R. (2003)
Quatre couleurs suffisent.
Londres. Livres de Pingouins.
Pour une histoire plus détaillée et technique, le livre de référence standard est:
Biggs, N.; Lloyd, E. &Wilson, R. (1986) (1998)
Théorie des graphes, 1736-1936
Oxford. Presse de l’Université d’Oxford.
Celui-ci nous met à jour, avec des fondations et une philosophie plus récentes.
Fritsch, R et Fritsch, G (2000)
Le Théorème des quatre couleurs: Histoire, Fondements Topologiques et Idée de preuve
New York. La version de Springer.
Presque aucun livre d’histoire générale n’a beaucoup de choses sur le sujet, mais le dernier chapitre de Katz intitulé « Ordinateurs et applications » a une section sur la Théorie des graphes, et le Théorème des Quatre couleurs est mentionné deux fois.
Polya G. Comment résoudre le problème.
C’est le livre classique sur la résolution de problèmes. Il y a eu de nombreuses éditions de ce livre depuis sa première apparition dans les années 1950 et il est encore facilement disponible. Curieusement, les éditions récentes ont étédevenu le sous-titre « Un nouvel aspect de la Méthode mathématique ».
Lakatos, I. (1976) Preuves andRefutations: La Logique de la Découverte mathématique.
Cambridge. C.U.P.
C’est un autre livre important qui a conduit à la recherche sur la résolution de problèmes et les enquêtes dans les années 1970. Il commence par une discussion en salle de classe entre un enseignant et un groupe d’étudiants sur la preuve de la formule d’Euler, et passe par les idées, les objections et les possibilités qui ont été réellement discutées par les mathématiciens et les scientifiques au XIXe siècle. Il soulève certaines des questions les plus importantes concernant l’enseignement et la résolution de problèmes d’apprentissage et les méthodes mathématiques et la preuve.
Références connexes
J’ai un petit livre sur les jeux de cordes depuis un certain temps. Quand j’étais à l’école, cela s’appelait le berceau du chat, et nous l’avons joué à notre époque.
Récemment, une revue française a publié un article sur l’algèbre des figures à cordes ! Si vous allez sur Amazon, vous trouverez un livre d’Ann Swain et Michael Taylor intitulé Finger Strings: A Book of Cats Cradles andString Figures qui sera publié par Floris books en septembre 2008. Il y a quelque 80 figures décrites avec des couleurs diagrams.It en spirale, il restera donc ouvert pendant que vous suivez les instructions. Il est également livré avec quelques boucles de cordes!
Pour les experts en nœuds, Le livre de nœuds cendré est un classique pour tous ceux qui s’intéressent aux centaines de nœuds de différents types et à leurs utilisations. Amazon adiverses éditions disponibles à différents prix.
Liens Web
Pour un aperçu général et des liens vers de nombreuses personnes et sujets, le site Web de l’auteur est
Et, bien sûr, les biographies de MacTuors des personnes impliquées dans le développement de tous les différents aspects mathématiques se trouvent à l’Index des biographies de MacTuors.
Le Théorème des Quatre Couleurs et trois Preuves. Pour le mathématiquementpersistant, le site Web suivant a une nouvelle approche intrigante pourattaquer le problème de la construction d’un nouvel algorithme pour résoudre le problème, et lier pour réduire la dépendance à un ordinateur.http://www.emu.edu.tr/~cahit/the%20four%20color%20theorem%20—%20three%20proofs.htm
Pour la théorie des graphes, Wikipedia donne un bon aperçu, et vous pouvez maîtriser les choses vraiment techniques. Il montre les types de modernesapplications de ce domaine des mathématiques. Si vous allez à GraphColouring et cliquez sur le Théorème des quatre couleurs, vous trouverez beaucoup plus d’informations.
Une histoire intéressante et pas trop technique de la Théorie des nœuds – comment une idée de la Physique de Kelvin revient aujourd’hui à la Théorie atomique.
L’Association des Professeurs de Mathématiques a des affiches de conception de nœuds celtiques. Allez sur leur site Web et parcourez la liste alphabétique des ressources.
Découvrez tout sur les nœuds sur l’Atlas des nœuds ! Si vous n’êtes pas un expert – profitez simplement de la variété et de la complexité de la base de données « dans l’esprit du wiki »
Plus artistique et colorée – mais non moins mathématique est le site de l’intrigue Knot.
Pour ceux qui veulent des trucs originaux et des détails historiques, allez à l’Histoire de la Théorie des nœuds sur: