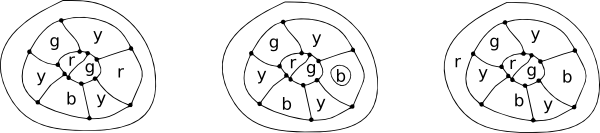
Nelivärilause
nelivärinen konjektuuri esitettiin ensimmäisen kerran hieman yli 150 vuotta sitten, ja se todistettiin lopullisesti vuonna 1976. Se on erinomainen esimerkki siitä, miten vanhat ideat yhdistyvät uusiin löytöihin ja tekniikoihin eri matematiikan aloilla, jotta ongelmaan voidaan löytää uusia lähestymistapoja. Se on myös esimerkki siitä, miten apparentlysimple ongelma oli ajateltu olevan ”ratkaistu”, mutta sitten tuli morecomplex, ja se on ensimmäinen mahtava esimerkki, jossa tietokone oli mukana todistamassa matemaattinen lause.
alussa
otaksuma, jonka mukaan mikä tahansa kartta voitaisiin värittää vain neljällä värillä, esiintyi ensimmäisen kerran kirjeessä, jonka Augustus De Morgan (1806-1871), new University College Londonin ensimmäinen matematiikan professori, kirjoitti ystävälleen William Rowanhamiltonille (1805-1865), kuuluisalle irlantilaiselle matemaatikolle vuonna 1852. Se oli ehdottanut De Morgan yksi hänen oppilaansa, FrederikGuthrie, puolesta hänen vanhempi veljensä Francis (jotka myöhemmin becameprofessor matematiikan yliopistossa Kapkaupungissa).


Augustus De Morgan (1807-1871) andWilliam Rowan Hamilton (1805-1865)
ongelma, niin yksinkertaisesti kuvattu, mutta niin tantalizingly vaikea todistaa, kiinni mielikuvitus monet matemaatikot at thetime. Kun myöhään 1860-luvulla De Morgan jopa otti ongelman ja hänenproof Amerikkaan, jossa muun muassa Benjamin Peirce (1809-1880) afamous matemaatikko ja tähtitieteilijä, tuli kiinnostunut siitä kuin pois kehittää hänen loogisia menetelmiä.
De Morgan käytti hyväkseen sitä, että kartassa, jossa on neljä aluetta ja kolme muuta, yksi niistä on kokonaan muiden saartama. Koska hän ei kyennyt todistamaan tätä, hän käytti sitä aksioomana , hänen todistuksensa perustana.
kopio De Morganin alkuperäisistä kirjoituksista hänen kirjeessään Hamiltonille ja yksinkertainen nelivärikartta.
vuonna 1878 Arthur Cayley (1821-1895) kysyi LondonMathematical Societyn kokouksessa, oliko kukaan löytänyt ratkaisua forDe Morganin alkuperäiseen kysymykseen, mutta vaikka oli ollut kiinnostusta, kukaan ei ollut edistynyt merkittävästi. Cayley becameinterested ongelman ja vuonna 1879 julkaistu lyhyt paperOn väri, mapswhere hän selitti joitakin vaikeuksia yrittää todiste ja teki joitakin tärkeitä osuuksia siitä, miten ongelma wasapproached. Hänen kysymyksensä kuuluu: ”Jos jokin kartta on jo onnistuneesti värjätty neljällä värillä ja lisäämme siihen toisen alueen, voimmeko säilyttää saman värityksen?”alkoi toinen linja ofenquiry, joka johti soveltamiseen mathematicalinduction on ongelma.

Arthur Cayley (1821-1895)
Arthur Cayley osoitti, että jos neliväriä oli jo käytetty kartan värittämiseen ja uusi alue oli lisätty, alkuperäväritystä ei ollut aina mahdollista säilyttää.
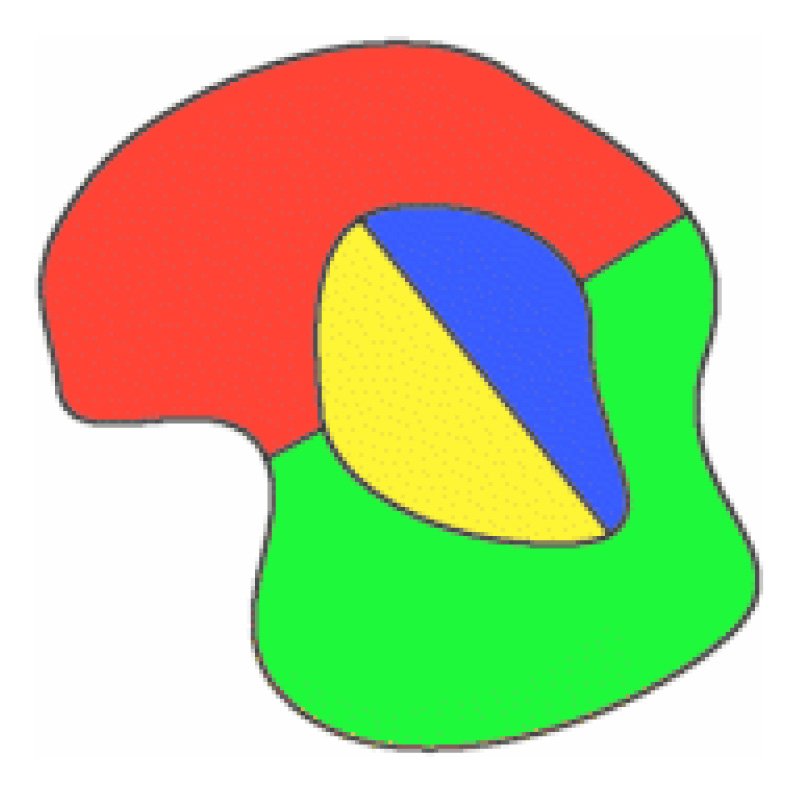
yllä kaikki neljä väriä on käytetty alkuperäisessä kartassa,ja sen ympärille on piirretty uusi alue. Tällöin punainen alue vaihdetaan siniseksi, jotta punaista voidaan käyttää uudella ympäröivällä alueella.
Cayley huomautti myös, että eräs versio ongelmasta oli mahdollista ratkaista rajoittamalla tapaa, jolla rajat kohtasivat. Esimerkiksi kartat, joissa vain kolme maata kokoontui on kolme reunat kokouksessa avertex. Näitä kutsutaan ”kuutiokartoiksi”, ja seuraavassa keskustelussa käytetyt kartat ovat kaikki kuutiokarttoja. Lisäksi jos kartta voidaan värittää neljällä värillä, rajalle ilmestyy vain kolme väriä.
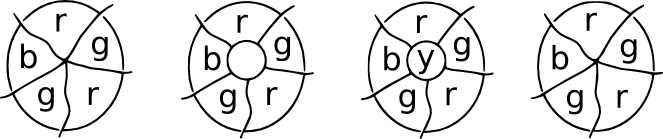
Paikkausdemonstraatio. Kuvitelkaapa, että jossakin kartan kohdassa joukko maita kohtaa toisensa. Nyt paikata kokouspaikka, ja kaikki uudet kokouspaikat on kolme rajoja peräisin niistä. Nämä ovat kuutiokarttoja, ja keskialueelle voidaan käyttää neljättä väriä. Kun laastari poistetaan, voimme palata alkuperäiseen väritykseen.
joitakin vanhoja tekniikoita, uusia olosuhteita ja lisää ongelmia!
voidaksemme seurata ongelman kehitystä meidän on tutkittava lyhyesti joitakin ajatuksia, menettelyjä ja tekniikoita, joita matemaatikot kehittivät yrittäessään ratkaista ongelmaa.
ainoat viisi naapuria arvelevat
” Jos et voi ratkaista apartikulaarista ongelmaa, etsi helpompi, jonka voit ratkaista.”(Polja. Miten ratkaista se)
” jokaisessa kartassa on vähintään yksi maa, jossa on viisi tai vähemmän naapureita.”
Kuvittele kartta meren ympäröimästä saaresta. Saaren Maiden värityksessä meri lasketaan oneregioniksi. Joissakin maissa voi olla vain kaksi rajaa (digoni), joissakin kolme (kuten kolmiossa), joissakin neljä (neliö) ja joissakin viisi (apentagon) tai enemmän.
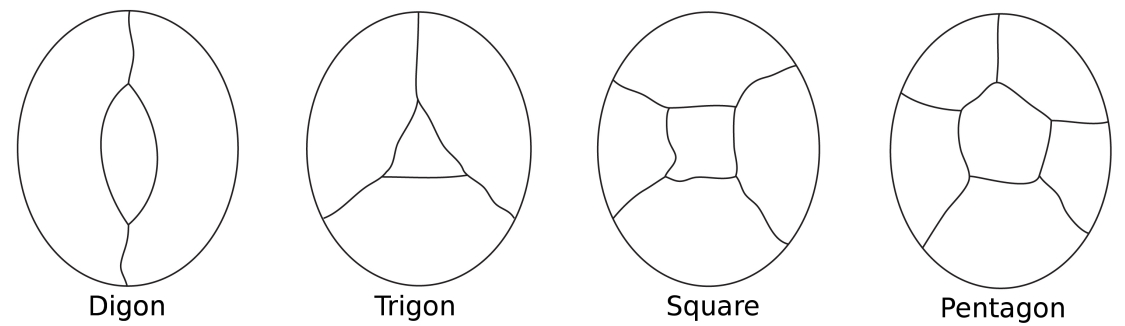
yksinkertaisimmat mahdolliset keskusalueen ympärysmitat.
Huomaa, että kaikissa näissä kokoonpanoissa jokaisessa solmussa on vain kolme solmua.
vuonna 1813 Augustin Cauchy (1759-1857) muokkasi monitahokkaalle Eulerin kaavan kahteen ulottuvuuteen asettamalla monitahokkaan tasolle, jolloin muodostuu thesolidin verkko. Näin kaavasta tuli $f + v – E = 1$, koska Cauchy ei laskenut verkon ”ulkopuolista” aluetta.

Augustin Cauchy (1759-1857)
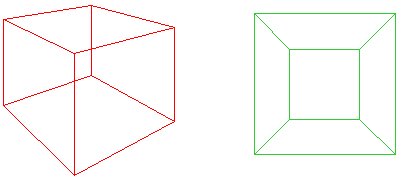
kuvittele litistäväsi punaisen kuution alas tasoon niin, että sen pohja aukeaa muodostaen vihreän verkon ulkopuolen. Cauchyn ajatus oli leikata pois yksi kasvot thecube, niin, että tason monikulmio, $f + v-E = 1$. Vaihtoehtoisesti, jos verkon ”ulkopuolta” pidetään infinitearean tahkona, niin meillä on edelleen $f + v – e = 2$
voimme olettaa, että jokaisesta kohtauspaikasta (vertices)nousee vähintään kolme reunaviivaa (reunaviivaa).
todiste siitä, että kartassa on vähintään yksi maa viiden tai harvemman naapurimaan ympäröimänä, on ristiriitainen. Jos tämä johtaa järjettömyyteen, meillä on todisteet.
laita nyt nämä arvot Eulerin kaavaan: $$f + v – e = 2$$ ja meillä on $1/3(e) + 2/3(e) – e $$ joka on nolla!
Tämä on absurdius, joten alkuperäinen olettamuksemme oli väärä.Tämä tarkoittaa, että on oltava vähintään yksi maa, jossa on viisi tai vähemmän naapureita!
Minimal Criminals!
toinen tapa puuttua neliväriongelmaan on olettaa, että se on FALSE, ja katsoa, mihin tämä johtaa. Oletetaan, että on olemassa karttoja, jotka tarvitsevat viisi väriä tai enemmän, ja valitsemme kartat, joissa on mahdollisimman pieni määrä maita. Näitä karttoja kutsutaan minimaalisiksi vastaesimerkeiksi tai minimaalisiksi rikollisiksi !
tämä tarkoittaa siis sitä,että minimaalista rikollista ei voi värittää neljällä värillä, mutta mikä tahansa kartta, jossa on vähemmän maita, voidaan värittää neljällä värillä. Jos voimme osoittaa, ettei minimirikollisia voi olla olemassa, voimme ehkä edistyä.
voimme esimerkiksi osoittaa, että minimaalinen rikollinen ei voi hillitä digonia.
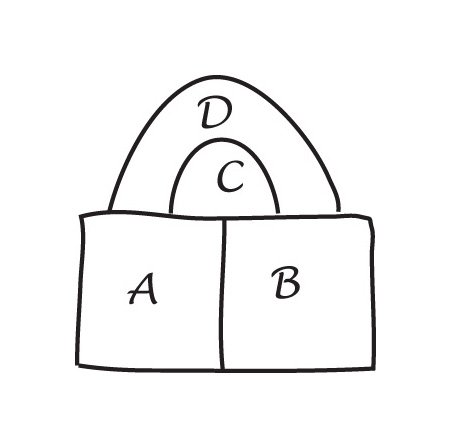
alkuperäisestä kartasta otetaan raja pois digonilta, ja saadaan uusi kartta, jossa on vähemmän maita. Tämä kartta voidaan värittää neljällä värillä (olettamuksestamme). Sitten väri tämä newmap, (tarvitsemme vain kaksi väriä). Vaihda poistamamme raja ja väritä kartta uudelleen. Olemme käyttäneet kolmea väriä, ja koska on vielä yksi väri käytettävissä, tämä osoittaa, että karttamme voidaan värittää neljällä värillä. Mutta tämä on vastoin oletustamme, joten minimirikollinen ei voi pitää digonia.
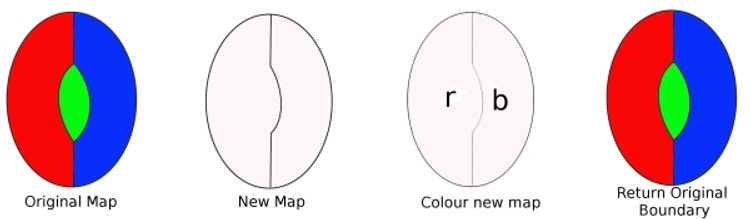
osoittaakseen, että Minimirangaistuskannoissa on kaksireunainen alue (digoni). Oletetaan, että on olemassa minimaalinen rikollinen, joka sisältää digonin. Reunan poistaminen tarkoittaa, että kartta sisältää vähemmän alueita. Uusi kartta voidaan siis värittää neljällä värillä. Vaihda nyt menetetty reuna. Koska aiemmin tarvittiin vain kaksi väriä, reunan korvaaminen tarkoittaa sitä, että voimme käyttää kolmatta väriä ja vielä neljättä väriä. Minimaalikriminaalin voi siis värittää neljällä värillä. Näin ollen minimikriminaali ei voi sisältää digonia.
tämä menettely voidaan toistaa osoittaakseen, että minimirangaistuskannoissa on kolmisivuinen maa (trigoni), mutta se hajoaa, kun kokeilemme tekniikkaa neliöllä, koska kun korvaamme nelikulmion, sen vieressä olevat maat saattavat hyvinkin käyttää kaikkia neljää väriä, joten todistusmenettely epäonnistuu. Kun tämä on tapahtunut, on selvää, että se ei toimi viisikulmioilla ja niin edelleen.
kuuden värin teoreemaa
voidaan soveltaa samantapaista tekniikkaa osoittamaan, että kuuden värin teoreema on tosi. Ensinnäkin oletamme, että ei ole olemassa karttoja, joita voidaan värittää kuudella värillä. Osa kartoista voidaan värittää seitsemällä värillä, joten jos voimme osoittaa, että se on mahdollista värittää alle seitsemällä värillä, olemme saavuttaneet tavoitteemme.
viiden naapurin teoreeman todistuksesta on mahdollista, että minimaalisen rikollisen idean avulla voidaan osoittaa, että mikä tahansa kartta voidaan värittää kuusivärillä!
alueilta solmuihin, verkostoihin ja topologiaan
vuonna 1879 Alfred Kempe (1849-1922) aloitti ”viiden naapurin kiinteistöstä” ja kehitti ”Kempe-ketjujen” menetelmänä tunnetun menetelmän löytääkseen todisteen neljän värin lauseesta. Hän julkaisi tämän todistusaineiston American Journal of Mathematics. Hän löysi kaksi yksinkertaisempaa versiota, jotka julkaistiin seuraavana vuonna, ja hänen todistuksensa oli kymmenen vuotta ennen Percy Heawood (1861-1955) osoitti, että Kempe oli käyttänyt merkittävää virhettä todiste-menetelmässä.


Alfred Kempe (1849-1922), PeterGuthrie Tait (1831-1901) ja Percy heawood (1861-1955)
vuonna 1880 P. G. Tait (1831-1901) matemaattinen fyysikko tarjosi ongelmaan ratkaisua. Itsenäisesti, Tait oli perustettu, ettämaps jossa parillinen määrä rajalinjat täyttävät jokaisessa pisteessä, voitaisiin värittää kaksi väriä, vaikka tämä tulos oliappeared aiemmin Kempe papers.
vuosien 1876-77 aikana Tait tuli tunnetuksi solmujen tutkimisesta ja luokittelusta. Tuolloin oli olemassa useita eri teorioita atomien rakenteesta. William Thompson (myöhemmin Lordi Kelvin 1824-1907) esitti fyysikko Hermann von Helmholtzin (1821-1894) kokeiden innoittamana ateorian, jonka mukaan atomit olivat solmittuja eetteriputkia. Kelvin ’s theory of’ Votex atoms ’ otettiin vakavasti noin kaksikymmentä vuotta, ja itinspired Tait sitoutuvat luokittelu solmua. Tait, Thomsonja James Clark Maxwell (1831-1879) keksivät tutkimuksissaan monia topologisia ajatuksia. Kelvinin teoria oli kuitenkin fundamentallymistaken ja fyysikot menettivät kiinnostuksensa Taitin työhön.


Hermann von Helmholtz (1821-1879),Lordi Kelvin (1824-1907) ja James Clark Maxwell (1831-1879)

Tait alkoivat tavoista, joilla yhdensuljettu narusilmukka voitiin solmia. Hänellä ei ollut alussa systemaattista menetelmää, ja hän aloitti intuitiivisesti ottamalla yhden suljetun silmukan ja kokeilemalla tapoja, joilla se voitaisiin solmia. Tietenkin, johto oli auki (kuten ashoelace) sitten solmittu, ja liittyi. Huomaa,että jos seuraatkordia solmun ympäri, ”over-under” – risteykset vuorottelevat.Sitten hän jatkoi kokeilla kaksi silmukkaa ja tapoja, joilla he voisivat olla solmittu yhteen. Kuvassa on solmuja, joissa on jopa kuusikertoja yhdelle silmukalle.
yksi Taitin tutkimuksen tuloksista oli hänen Hamiltonin kuvaajan konjektuuri.
karttaa pidetään pallolle piirrettynä monitahokkaana, joka voidaan projisoida tasolle. Tait ehdotti, että mikä tahansa cubicpolyhedral kartta on Hamiltoniancycle . Tait ’ s menetelmä keskittynyt reunat kuvaajan andhe osoitti, että Hamiltonin sykli voisi tuottaa neljä-väritys OFA kartta. Se ei ollut vasta 1946, että William Tutte (1917-2002) löydettyensimmäinen counterexample, Tait ’ s arveluihin.
Tait ja yhteys solmuihin
Taitinaloitti snarkien tutkimuksen vuonna 1880, jolloin hän todisti nelivärilauseen vastaavan väitettä, jonka mukaan no snark isplanar. A planar kaavio on yksi, joka voidaan piirtää tasossa withno reunat ylittävät. Näyttää siltä, Tait ’ s ajatus ei-planar graphsmight ovat peräisin hänen tutkimus solmua ja Hamiltonin polkuja .
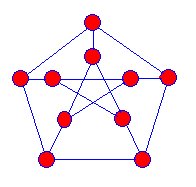
ensimmäinen tunnettu snark oli vuonna 1898 löydetty Petersenin graafi,ja matemaatikot alkoivat metsästää lisää tällaisia grafiikoita, mutta vasta vuonna 1946 löydettiin toinen snark.
 |
|
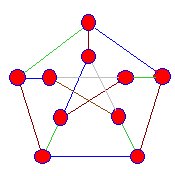 |
tämän nokan kärkipisteet täyttävät reunat ovat väriltään sinisiä,vihreitä ja ruskeita, mutta päädymme aina vaiheeseen, jossa tätä prosessia ei voida jatkaa. |

Julius Peterson (1839-1910)
Julius Peterson (1839-1910)
hunting of thesnark on Lewis Carrollin kirjoittama runo, ja Martin gardnernamed these graphs snarks, koska ne olivat niin vaikeasti tavoitettavia.
ongelman muuttaminen ja uusien menetelmien löytäminen.
vaikka Heawood löysi vuonna 1890 Kempen todistusmenetelmästä suurimman virheen, hän ei kyennyt todistamaan neljän värin teoreemaa, mutta hän teki merkittävän läpimurron ja todisti lopullisesti, että kaikki kartat voitiin värittää viidellä värillä.
heawood teki monia merkittäviä osuuksia ongelman ratkaisemiseksi,siirtäen huomion keskipisteen kartan alueilta niiden välisille rajanylityspaikoille. By 1898 hän oli osoittautunut, että jos määrä ofedges noin kunkin alueen on jaollinen 3 sitten alueet couldbe värillinen Neljä väriä.
Cauchyn todistus Eulerin kaavasta sisälsi myös ajatuksen, että monitahokkaan netosta voidaan triangulatoida lisäämällä särmiä makenonin-kolmionmuotoisiin tahkoihin kolmioiksi. Sitten hän kehitti procedurewhereby hän poisti reunat yksitellen, mikä osoittaa, että Euler nformula voitaisiin säilyttää jokaisessa vaiheessa.
Cauchyn todistus Eulerin kaavasta
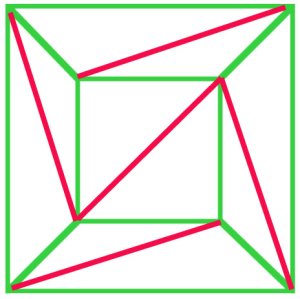
Cauchyn todistus Eulerin kaavasta 1813 alkoi ajatuksella monitahokkaan aprojektiosta tasoverkon saamiseksi. Hän furtherdemonstrated (A), että kaikki net voitaisiin triangulated, ja hänen todiste(b), Euler kaava hyväksyttiin tuolloin.
 (a)
|
In principle, every polygonal net can be triangulated. In thisnet of a cube (a), $f + v – e$ is $10 + 8 – 17 = 1$, and Euler’sformula still holds. |
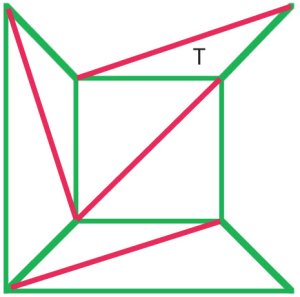 (b)
|
Cauchyn argumentti oli poistaa ulkoreunat kaaviosta(a) yksitellen, ja kun hän pääsi vaiheeseen kuten kaaviossa (B)poistettu koko kolmio t, mikä säilyttää Eulerin kaava. 1800-luvun alun manymatematikot olivat yhtä mieltä siitä, että tämä menettely osoitti todisteen Eulerin kaavasta allpolyhedralle. |
vuoteen 1900 mennessä matemaatikot tiesivät, että mistä tahansa kartasta voidaan rakentaa tasokuvio käyttäen voimakasta kaksinaisuuden käsitettä . Duaalikielessä alueita edustavat vertices ja kaksi vertices ovat liittyneet yhteen reunoilla, jos alueet ovat vierekkäisiä. Näissä kaavioissa, FourColour arveluihin nyt kysyy, jos vertices, kuvaaja voi becoloured kanssa 4 väriä niin, että ei kaksi vierekkäistä vertices ovat thesame väri.
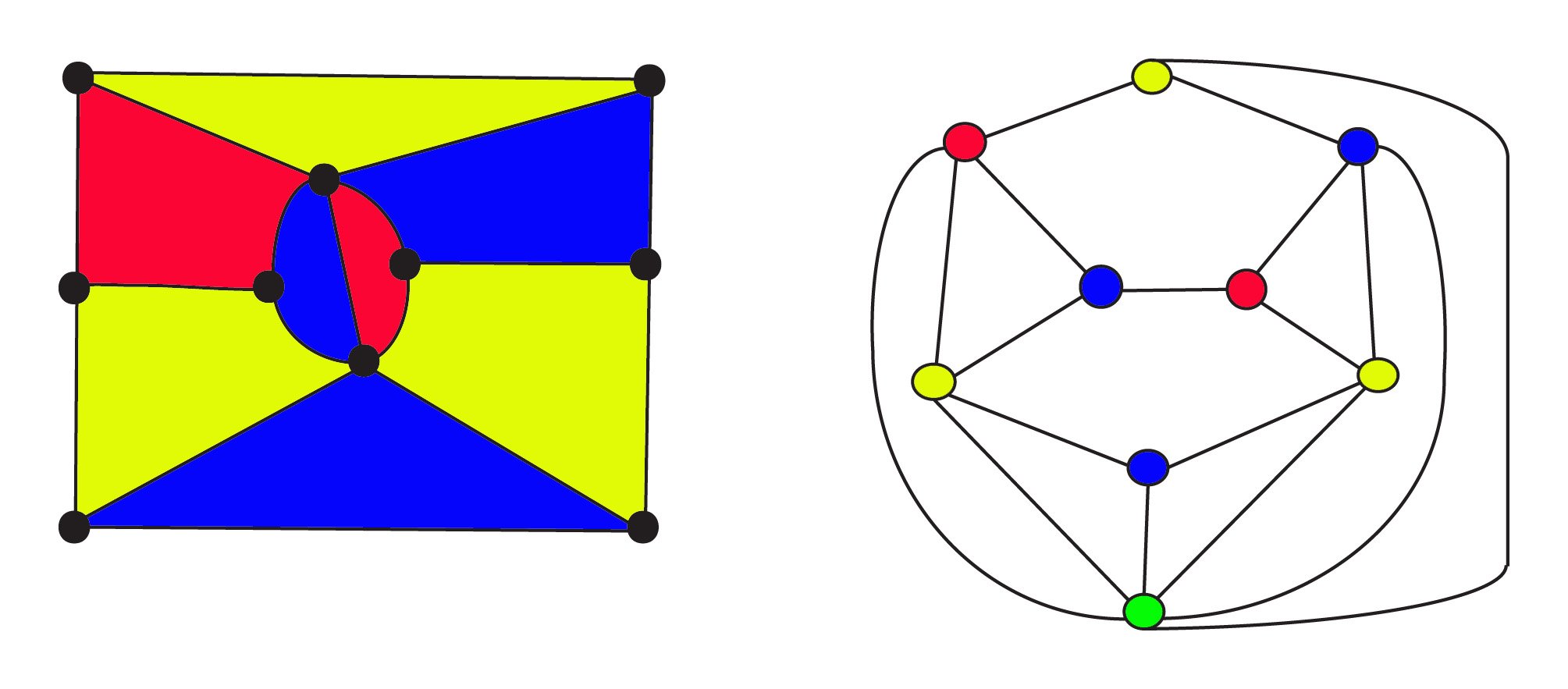
vasemmalla 3-värisellä kartalla on$8$ alueet $10$ verteksit ja $17$ edges. Sen dual graafi theright on $9$ alueilla $9$ vertices ja $17$ edges jossa thevertices ovat värillisiä sama kuin alueilla kartan. Kuvaajan alareunassa oleva greenvertex edustaa kartan ääretöntä ulkoaluetta. Sekä alkuperäinen kartta että sen kaksoiskartta noudattavat Eulerin formulaa verkoille $f + v-e = 1$ tai, $\text{regions} +\text{vertices} – \text{edges} = 1$. Duaalisuusrelaatio issymmetrinen: duaalikäyrän duaalikäyrä on alkuperäinen kuvaaja, jossa vaihdetaan alueita ja kärkipisteitä.
1900-luvun alkupuoliskolla mathematicians keskittyi muokkaamaan tällaisia tekniikoita yksinkertaistaakseen monimutkaisia karttoja erityistapauksiksi, jotka voitiin tunnistaa ja luokitella, tutkiakseen niiden erityisominaisuuksia ja kehittääkseen ajatuksen minimaalisesta karttakokoonpanosta, jota voitaisiin testata.
alun perin joukon ajateltiin sisältävän lähes 9 000 jäsentä, mikä oli valtava tehtävä,ja niin mathematiciansturned tietokonetekniikoita kirjoittamaan algoritmeja, jotka voisivat tehdä thetesting heille. Algoritmit käyttivät muunneltuja versioita Kempen alkuperäisistä käsityksistä ketjuista yhdessä muiden tekniikoiden kanssa minimijoukon jäsenmäärän pienentämiseksi.
tehtyään yhteistyötä John Kochin kanssa reducibility-ongelman parissa Illinoisin yliopistossa vuonna 1976 Kenneth Appeland Wolfgang Haken vähensi lopulta testausongelman välttäväksi asetukseksi, jossa oli 1936 kokoonpanoa, ja täydellinen ratkaisu neljän värin arveluihin saavutettiin. Tämä karttojen vähennettävyyden tarkistamisen ongelma yksitellen tarkistettiin kaksinkertaisesti eri ohjelmilla ja eri tietokoneilla. Ne osoittivat, että vähintään yhtä karttaa, jossa on mahdollisimman pieni määrä viittä väriä edellyttäviä alueita, ei voi olla olemassa.
ensimmäisen todisteen jälkeen 4-värityskartoille on löydetty tehokkaampia algoritmeja, ja vuoteen 1994 mennessä väistämätön joukko oli kutistunut 633: een.
onko tietokoneella tehty ”todiste” oikea todiste?
koska todisteet tehtiin tietokoneen avulla, syntyi välitön paheksunta. Monet matemaatikot ja filosofit väittivät, että todiste ei ollut oikeutettu. Jotkut sanoivat, että vain ihmisten, ei koneiden, olisi ”todistettava” todisteet, kun taas toiset, jotka ovat käytännönläheisempiä, kyseenalaistivat algoritmien luotettavuuden ja koneiden kyvyn suorittaa ne virheettömästi.Monet matemaatikkojen kirjoittamista todisteista on kuitenkin todettu virheellisiksi, joten väite luotettavuudesta tuntuu tyhjältä.Esitetyistä mielipiteistä riippumatta tilanne johti vakavaan keskusteluun todisteiden luonteesta, joka jatkuu edelleen.
pedagogiset muistiinpanot:
Käytä tämän artikkelin yläreunassa olevaa muistiinpanoja-välilehteä tai klikkaa tästä .
toteaa
- yksityiskohtaisemmin tästä ja muista tässä jaksossa esiintyvistä menettelyistä on nähtävissä Robin Wilsonin kirjassa Four Colours Enough .
- solmut voivat olla vasenkätisiä tai oikeakätisiä, ja nykyään tälle ominaisuudelle on tärkeitä sovelluksia kemiassa, farmasiassa,biologiassa ja fysiikassa.
- nimetty William Rowan Hamiltonin (1805-1865) mukaan. A Hamiltonin polku on kaavio visitseach huippupiste täsmälleen kerran. A Hamiltonin sykli (tai piiri) on apath joka vierailee kunkin huippupiste täsmälleen kerran ja palaa thestarting huippupiste.
- Imre Lakatoksen kirja Proofs and Refutations sisältää keskustelua ja kritiikkiä Cauchyn menettelystä (sivut 6 – 12), ja paljon enemmän Eulerin lauseen tarinasta.
- ajatus kaksinaisuudesta syntyi 1500-ja 1600-luvuilla projektiivisen geometrian kehityksen myötä. Matemaatikot kuten Pascal ja desargues havaitsivat, että uusia teoreemoja voitaisiin löytää vaihtamalla termejä ”piste” ja ”viiva” tiettyjen geometristen konfiguraatioiden kuvauksissa. Esimerkki on säännöllisissä monitahokkaissa, joissa yhden kärjet vastaavat toisen tahkoja. Tetraedrin duaalikappale on siis toinen tetraedri ja kuution duaalikappale on oktaedri. Duaalikappale on originaalipolyedri.
parhaiten suosittu, helppolukuinen kirja Neliväristä on:
Wilson, R. (2003)
Neljä väriä riittää.
Lontoo. Penguin Books.
standardreference-kirja on perusteellisempi ja teknisempi:
Biggs, N.; Lloyd, E. & Wilson, R. (1986) (1998)
Graph Theory, 1736-1936
Oxford. Oxford University Press.
Tämä tuo meidät ajan tasalle, uudempiin perustuksiin ja filosofiaan.
Fritsch, R and Fritsch, G (2000)
The Four Color Theorem: History,Topological Foundations, and Idea of Proof
New York. Springer-Verlag.
tuskin yhdessäkään yleisessä historiateoksessa on aiheesta paljonkaan, mutta Katzin viimeisessä luvussa ”tietokoneet ja sovellukset” on kohta Graafiteoriasta, ja neljän värin lause on mainittu kaksi kertaa.
Polya G. Miten SolveIt.
Tämä on klassikkokirja ongelmanratkaisusta. Kirjasta on otettu useita painoksia sen ilmestyttyä 1950-luvulla, ja se on edelleen helposti saatavilla. Kummallista kyllä, viime aikoina julkaistut painokset ovat saaneet alaotsikon ”a new aspect of Mathematical Method”.
Lakatos, I. (1976) Proofs andRefutations: the Logic of Mathematical Discovery.
Cambridge. C. U. P.
Tämä on toinen tärkeä kirja, joka johti tutkimuksen intoProblem Solving ja tutkimukset 1970-luvulla. Se alkaa aclassroom keskustelu välillä opettaja ja ryhmä studentsabout todiste Euler kaavaa, ja vaihtelee läpi ideoita,vastalauseita ja mahdollisuuksia, jotka todella keskusteltiin bymathematicians ja tutkijat yhdeksännentoista vuosisadan. Se nostaa esiin tärkeimmät kysymykset opetuksesta ja oppimisesta ongelmanratkaisusta sekä matemaattisista menetelmistä ja todisteista.
aiheeseen liittyviä viittauksia
Minulla on ollut jo jonkin aikaa pieni kirja Jousileikeistä. Kun olin koulussa, sen nimi oli Cat ’ s Cradle, ja soitimme sitä meidän aikanamme.
äskettäin eräs ranskalainen lehti on julkaissut tutkielman string-lukujen’ algebrasta’! Jos menet Amazon löydät anice kirja Ann Swain ja Michael Taylor nimeltään Finger Strings: kirja Cats Cradles andString luvut julkaistaan Floris books syyskuussa 2008. Värillisellä kuvattuja lukuja on noin 80 diagrams.It spiraali on sidottu, joten se pysyy auki, kun seuraat ohjeita. Mukana tulee myös pari narusilmukkaa!
solmujen asiantuntijoille solmujen AshleyBook on klassikko kaikille, jotka ovat kiinnostuneita erilaisten solmujen oksista ja niiden käyttötarkoituksista. Amazon onerilaisia versioita saatavilla eri hintoihin.
www-linkit
yleiskatsauksen ja linkkejä moniin henkilöihin ja aiheisiin saa actutor-sivustolta
ja tietenkin MacTutor-Elämäkerrat kaikista eri matemaattisista näkökulmista löytyvät MacTutor-Elämäkerrat-indeksistä.
neljän värin lause ja kolme todistusta. Jotta mathematicallypersistent seuraava sivusto on kiehtova uusi lähestymistapa attacking ongelma rakentaa uuden algoritmin ratkaisemaanongelma, ja sitominen vähentää riippuvuutta tietokoneeseen.http://www.emu.edu.tr/~cahit/the%20four%20color%20theorem%20—%20three%20proofs.htm
Graafiteorialle Wikipedia antaa hyvän yleiskuvan, ja siitä voi skipata todella teknisiä juttuja. Se osoittaa erilaisia modernapplications tällä alalla matematiikka. Jos siirryt GraphColouring ja klikkaa neljän värin lause, niin löydät paljon lisätietoja.
mielenkiintoinen, eikä liian tekninen Solmuteorian historia-miten Kelvinin fysiikan idea palaa Atomiteoriaan tänään.
matematiikan opettajien liitolla on kelttiläisiä Knotdesign-julisteita. Mene niiden verkkosivuilla ja selata aakkosellinen luettelo resursseja.
ota selvää solmuista Solmukartastossa! Jos et ole asiantuntija-nauti vain tietokannan ”inthe spirit of wiki”moninaisuudesta ja monimutkaisuudesta
taiteellisempi ja värikkäämpi – mutta yhtä matemaattinen on theKnot Plot Site.
niille, jotka haluavat jotain alkuperäistä tavaraa ja historicaldetail mennä Solmuteorian historiaan: