El Teorema de los Cuatro Colores
La Conjetura de los Cuatro Colores se estableció por primera vez hace poco más de 150 años, y finalmente se demostró de manera concluyente en 1976. Es un ejemplo sobresaliente de cómo las ideas antiguas se combinan con nuevos descubrimientos y técnicas en diferentes campos de las matemáticas para proporcionar nuevos enfoques a un problema. También es un ejemplo de cómo se pensaba que un problema aparentemente simple estaba «resuelto», pero luego se convirtió en más complejo, y es el primer ejemplo espectacular en el que una computadora participó en la demostración de un teorema matemático.
Al principio
La conjetura de que cualquier mapa podría ser coloreado usando solo cuatro colores apareció por primera vez en una carta de Augusto De Morgan (1806-1871), primer profesor de matemáticas en el new University College de Londres, a su amigo William Rowanhamilton (1805-1865), el famoso matemático irlandés en 1852. Fue sugerido a De Morgan por uno de sus estudiantes, FrederikGuthrie, en nombre de su hermano mayor Francis (quien más tarde se convirtió en profesor de matemáticas en la Universidad de Ciudad del Cabo).


Augustus De Morgan (1807-1871) y William Rowan Hamilton (1805-1865)
El problema, tan simple descrito, pero tan tentadoramente difícil de probar, atrapó la imaginación de muchos matemáticos en ese momento. A finales de la década de 1860, De Morgan incluso llevó el problema y su prueba a América, donde, entre otros, Benjamin Peirce (1809-1880), un famoso matemático y astrónomo, se interesó en él para desarrollar sus métodos lógicos.
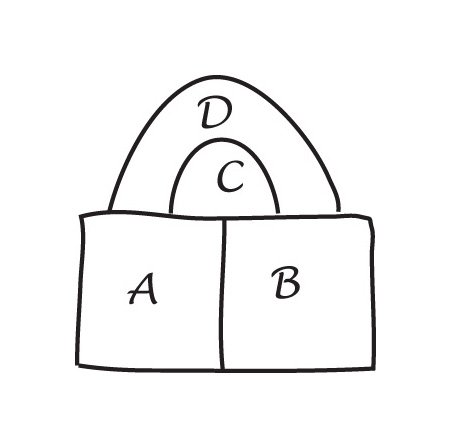
De Morgan utilizó el hecho de que en un mapa con cuatro regiones, cada una tocando las otras tres, una de ellas está completamente encerrada por las otras. Como no pudo encontrar una manera de probar esto , lo usó como un axioma, la base de su prueba.
Una copia de la carta original de De Morgan a Hamilton y un sencillo mapa a cuatro colores.
En 1878 Arthur Cayley (1821-1895) en una reunión de la LondonMathematical Society preguntó si alguien había encontrado una solución para la pregunta original dede Morgan, pero aunque había habido algún interés, nadie había hecho ningún progreso significativo. Cayley se interesó en el problema y en 1879 publicó un breve documento sobre la coloración de mapas, donde explicó algunas de las dificultades para intentar una prueba e hizo algunas contribuciones importantes a la forma en que se abordó el problema. Su pregunta era: «si un mapa en particular ya está coloreado con éxito con cuatro colores,y añadimos otra área, ¿podemos seguir teniendo el mismo color?»comenzó otra línea de investigación que condujo a la aplicación de lainducción matemática al problema.

Arthur Cayley (1821-1895)
Arthur Cayley mostró que si fourcolours ya había sido utilizada para colorear un mapa, y una nueva región wasadded, no siempre fue posible mantener la originalcolouring.
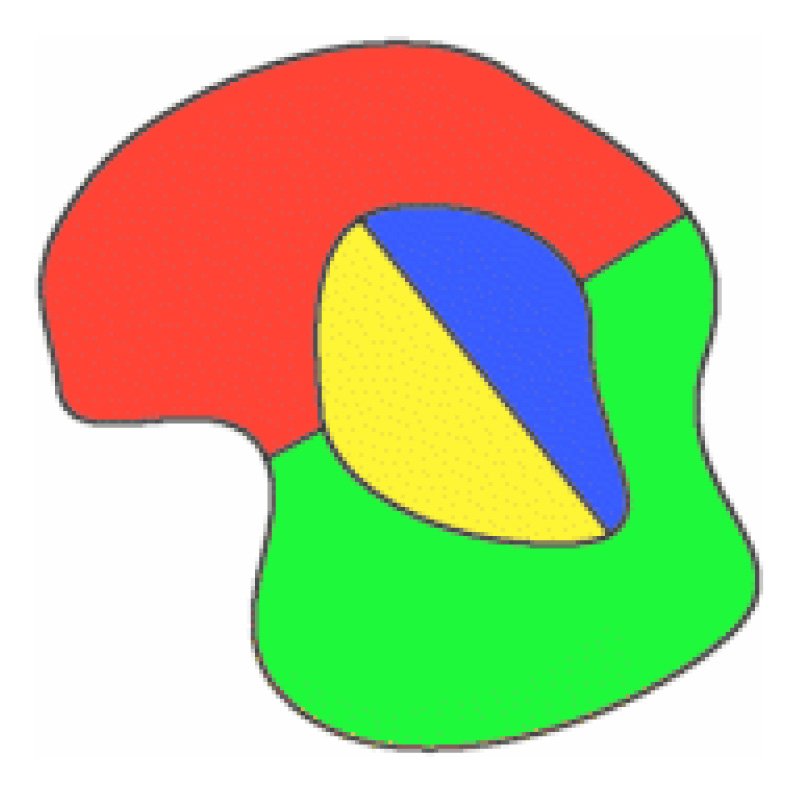
Arriba, los cuatro colores se han utilizado en el mapa original, y se dibuja una nueva región para rodearlo. En este caso, una región roja se cambia a azul, de modo que el rojo se puede usar en la nueva región circundante.
Cayley también observó que era posible resolver una versión del problema restringiendo la forma en que se cumplían los límites. Por ejemplo,los mapas en los que solo se reúnen tres países tienen tres bordes que se encuentran en avertex. Estos se denominan «mapas cúbicos», y los mapas utilizados en la siguiente discusión son todos mapas cúbicos. Además, si un mapa puede ser coloreado con cuatro colores, solo aparecerán tres colores en la frontera.
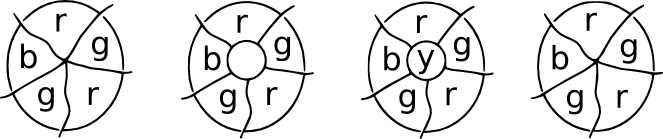
El Parche de demostración. Imagine que en algún lugar de un mapa se encuentran varios países en un punto. Ahora coloque un parche sobre el punto de encuentro, y todos los nuevos puntos de encuentro tendrán tres bordes que emanarán de ellos. Estos son mapas cúbicos, y se puede usar un cuarto color para la región central. Al retirar el parche, podemos volver a la coloración original.
Algunas técnicas antiguas, nuevas condiciones y más problemas!
Para seguir la evolución del problema, necesitamos investigar brevemente algunas de las ideas, procedimientos y técnicas que los matemáticos desarrollaron en sus intentos de resolverlo.
Los únicos Cinco Vecinos Conjeturan
‘Si no puedes resolver un problema concreto, busca uno más fácil que puedas resolver.»(Polya. Cómo resolverlo)
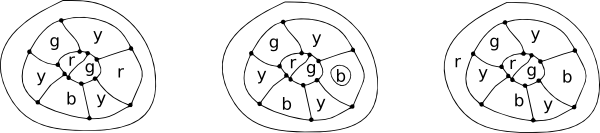
‘ Cada mapa tiene al menos un país con cinco vecinos o menos.’
Imagine un mapa de una isla rodeada por el mar. En el color de los países de la isla, contamos el mar como una región. Algunos países pueden tener solo dos fronteras (un digon), algo tres (como en un triángulo), unas cuatro (un cuadrado) y unas cinco (un apentágono) o más.
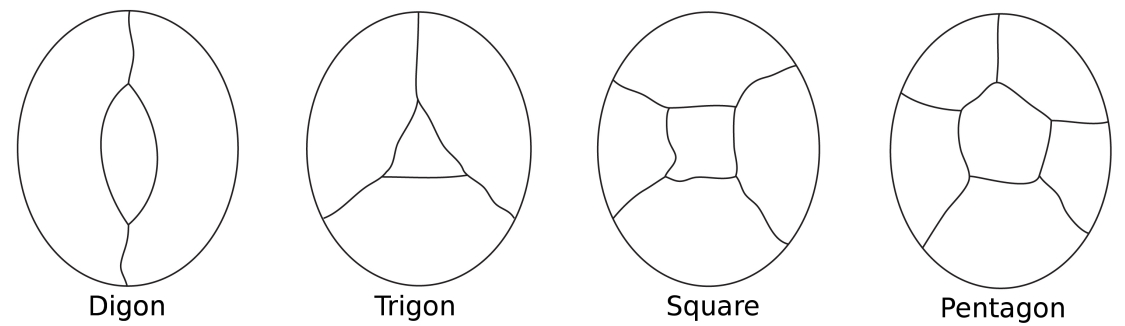
Las configuraciones posibles más simples para rodear una región central.Tenga en cuenta que en todas estas configuraciones, cada nodo solo tiene tres hileras.
En 1813, la fórmula de Euler para poliedros fue adaptada para dos dimensiones por Augustin Cauchy (1759-1857) proyectando el poliedro en un plano formando así la red del sólido. De esta manera, la fórmula se convirtió en f f + v – e = 1$, porque Cauchy no contaba la región ‘exterior’ de la red.

Augustin Cauchy (1759-1857)
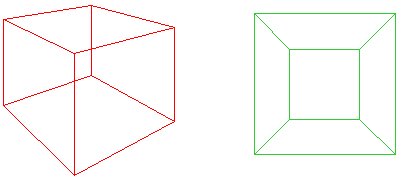
Imaginar aplastar el cubo rojo de la downonto un plano de tal manera que su base se abre para formar el outsideedge de la verde de la red. La idea de Cauchy era cortar una cara del cubo, de modo que para un polígono plano, f f + v – e = 1$. Alternativamente, si el ‘exterior’ de la red se considera como una cara con infinitearea, entonces todavía tenemos $f + v – e = 2
Podemos asumir que hay al menos tres líneas de borde (aristas)que emergen de cada punto de encuentro (vértices).
La prueba de que el mapa tiene al menos un país rodeado de cinco o menos vecinos procede por contradicción. Si esto lleva a un absurdo, tenemos una prueba.
Ahora pon estos valores en la fórmula de Euler: f f + v – e = 2 have y tenemos 1 1/3(e) + 2/3(e) – e! ¡que es cero!
Esto es lo absurdo, por lo que nuestra suposición original era falsa.Esto significa que debe haber al menos un país con cinco o menos vecinos!
¡Delincuentes mínimos!
Otra forma de abordar el problema de los cuatro colores es asumir que es falso y ver a dónde lleva esto. Supongamos que hay mapas que necesitan cinco colores o más, y elegimos los mapas con el menor número posible de países. ¡Estos mapas se llaman contraejemplos mínimos o criminales mínimos !
Esto significa que un criminal mínimo no puede ser coloreado con cuatro colores,pero cualquier mapa con menos países puede ser coloreado con cuatro colores. Si podemos demostrar que los criminales mínimos no pueden existir, entonces podríamos hacer algún progreso.
Por ejemplo, podemos demostrar que un criminal mínimo no puede contener un digon.
Del mapa original, quita un límite del digon y obtendremos un nuevo mapa con menos países. Este mapa se puede colorear con cuatro colores (de nuestra suposición). Luego coloreamos este mapa nuevo (solo necesitamos dos colores). Ahora reemplace el borde que eliminamos y vuelva a colorear el mapa. Hemos utilizado tres colores, y puesto que todavía hay un color más disponible, esto muestra que nuestro mapa puede ser coloreado con cuatro colores. Pero esto va en contra de nuestra suposición, así que un criminal mínimo no puede contener un digon.
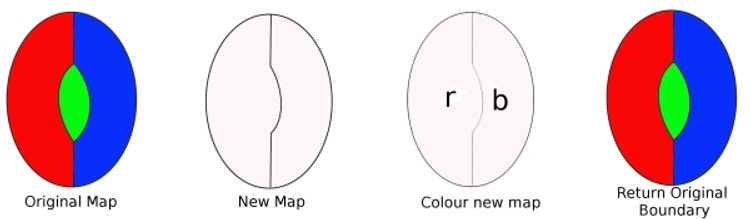
Para mostrar que una Mínima Criminalcannot contienen una región con dos bordes (un digon). Supongamos que hay un criminal mínimo que contiene un digon. Eliminar un borde significa que el mapa contiene menos regiones. Así que este nuevo mapa se puede colorear con cuatro colores. Ahora reemplace el borde perdido. Dado que antes solo se necesitaban dos colores, reemplazar el borde significa que podemos usar un tercer color y aún tener un cuarto color para usar. Por lo tanto, un minimalcriminal se puede colorear con cuatro colores. Por lo tanto, un criminal mínimo no puede contener un digon.
Este procedimiento se puede repetir para mostrar que un criminal mínimo no puede contener un país de tres lados (un trigon), pero se descompone cuando probamos la técnica en un cuadrado, porque cuando reemplazamos el cuadrado, los países al lado pueden usar los cuatro colores, por lo que el procedimiento de prueba falla. Una vez que esto ha sucedido, se vuelve obvio que no funcionará para pentágonos, y así sucesivamente.
El Teorema de los seis colores
Se puede aplicar una técnica similar para mostrar que el teorema de los seis colores es verdadero. En primer lugar, suponemos que no hay mapas que puedan ser coloreados con seis colores. Algunos de los mapas se pueden colorear con siete colores, por lo que seleccionando uno de estos (un criminal mínimo), si podemos demostrar que es posible colorearlo con menos de siete colores, hemos logrado nuestro objetivo.
De la prueba del teorema de los cinco vecinos, es posible proceder utilizando la idea criminal mínima para mostrar que cualquier mapa puede ser coloreado con seis colores!
De Regiones a Nudos, Redes y Topología
En 1879 Alfred Kempe (1849-1922), utilizando técnicas similares a las descritas anteriormente, partió de la «propiedad de los cinco vecinos» y desarrolló un procedimiento conocido como el método de las «Cadenas de Kempe» para encontrar una prueba del Teorema de los Cuatro Colores. Publicó esta prueba en el American Journal of Mathematics. Encontró dos versiones más simples que se publicaron al año siguiente, y su prueba duró diez años antes de que Percy Heawood (1861-1955) mostrara que había un error importante en el método de prueba que Kempe había utilizado.


Alfred Kempe (1849-1922), PeterGuthrie Tait (1831-1901) y Percy Heawood (1861-1955)
En 1880, P. G. Tait (1831-1901) un físico matemático, offereda solución al problema. Independientemente, Tait había establecido que los mapas donde un número par de líneas fronterizas se encuentran en cada punto,podían ser coloreados con dos colores, aunque este resultado había aparecido anteriormente en los documentos de Kempe.
Durante 1876-77 Tait se hizo bien conocido por su estudio y clasificación de nudos. En ese momento había una serie de teorías diferentes sobre la estructura de los átomos. William Thompson (más tarde, Lord Kelvin 1824-1907) inspirado en los experimentos del físico alemán Hermann von Helmholtz (1821-1894) propuso la ateoría de que los átomos eran tubos anudados de éter. La teoría de Kelvin de los átomos de vórtice se tomó en serio durante unos veinte años, y le inspiró a realizar una clasificación de nudos. Tait, Thomson y James Clark Maxwell (1831-1879) inventaron muchas ideas topológicas durante sus estudios. Sin embargo, la teoría de Kelvin fue ignorada y los físicos perdieron interés en el trabajo de Tait.


Hermann von Helmholtz (1821-1879),Lord Kelvin (1824-1907) y James Clark Maxwell (1831-1879)

Tait comenzó con las formas en que la puesta aúnicamente circuito cerrado de cable podría ser anudado. No tenía ningún método sistemático al principio, y comenzó de una manera intuitiva tomando un bucle cerrado único y experimentando con las formas en que se podía anudar. Por supuesto, el cordón tenía que estar abierto (como ashoelace), luego anudado y unido. Tenga en cuenta que si sigue el cordón alrededor del nudo, los cruces ‘sobre – debajo’ se alternarán.Luego pasó a experimentar con dos bucles y las formas en que se podían anudar juntos. Aquí se muestran nudos con hasta seis cruces para un solo bucle.
Uno de los resultados del estudio de Tait fue su conjetura de grafos hamiltonianos.
Un mapa es considerado como un poliedro dibujado sobre una esfera, y luego puede proyectarse sobre un plano. Tait propuso que cualquier mapa cubicopoliédrico tiene un Hamiltonianciclo . El método de Tait se centró en los bordes del gráfico y mostró que un ciclo hamiltoniano podía producir un mapa de cuatro colores. No fue hasta 1946 que William Tutte (1917-2002) encontró el primer contraejemplo a la conjetura de Tait.
Tait y la conexión con nudos
Tait Inició el estudio de snark en 1880, cuando demostró que el teorema de cuatro colores era equivalente a la afirmación de que no snark es plano. Un gráfico plano es uno que se puede dibujar en el plano sin cruzar bordes. Parece que la idea de Tait de gráficos no planos podría haber venido de su estudio de nudos y caminos hamiltonianos .
El primer snark conocido fue el grafo de Petersen descubierto en 1898,y los matemáticos comenzaron a buscar más de este tipo de grafos, pero no fue hasta 1946 que se encontró otro snark.
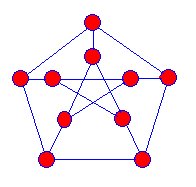 |
Snarks son proyecciones de tres dimensiones gráficos en theplane. No hay vértices donde los bordes azules parezcan cruzarse entre sí. Los Snarks tienen las siguientes propiedades:
|
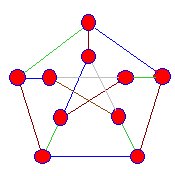
|
Los bordes que se encuentran con los vértices de este snark son de color azul,verde y marrón, pero siempre llegamos a una etapa en la que este proceso no puede continuar. |
Julius Peterson (1839-1910)
La Caza de theSnark es un poema escrito por Lewis Carroll, y Martin Gardnernamed estos gráficos Snarks, porque eran tan difícil de alcanzar.
Transformar el problema y encontrar nuevos métodos.
Aunque Heawood encontró la falla principal en el método de prueba de Kempe en 1890, no pudo probar el teorema de los cuatro colores, pero hizo un avance significativo y demostró de forma concluyente que todos los mapas podían ser coloreados con cinco colores.
Heawood hizo muchas contribuciones importantes al problema,desplazando el foco de atención de las áreas de un mapa a los límites entre ellas. En 1898 había demostrado que si el número de escalones alrededor de cada región es divisible por 3, las regiones podrían ser coloreadas con cuatro colores.
La prueba de Cauchy de la fórmula de Euler también incluyó la idea de que cualquier red de un poliedro puede ser triangulada agregando bordes a caras no triangulares en triángulos. Luego desarrolló un procedimiento en el que eliminó los bordes uno por uno, mostrando que la forma de Euler se podía mantener en cada paso.
La prueba de Cauchy de la Fórmula de Euler
La prueba de Cauchy de 1813 de la fórmula de Euler comenzó con la idea de la aproximación de un poliedro para obtener una red plana. Además, demostró (a) que cualquier red podía ser triangulada, y su prueba(b) de la fórmula de Euler fue aceptada en ese momento.
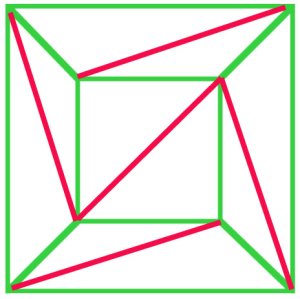 (a)
|
In principle, every polygonal net can be triangulated. In thisnet of a cube (a), $f + v – e$ is $10 + 8 – 17 = 1$, and Euler’sformula still holds. |
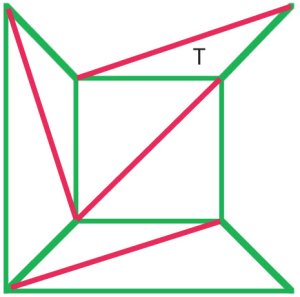 (b)
|
Cauchy argumento fue quitar los bordes externos del diagrama(a) uno por uno, y cuando llegó a una etapa, como en el diagrama (b)quita todo el triángulo T, preservando así la fórmula de Euler. Muchos matemáticos de principios del siglo XIX coincidieron en que este procedimiento demostraba una prueba de la fórmula de Euler para todos los políyedros. |
En 1900, los matemáticos sabían que un gráfico plano se podía construir desde cualquier mapa utilizando el poderoso concepto de dualidad . En el dual, las regiones están representadas por vértices y dos vértices están unidos por un borde si las regiones son adyacentes. En estos gráficos, la Conjetura de cuatro colores ahora pregunta si los vértices del gráfico pueden ser coloreados con 4 colores para que no haya dos vértices adyacentes del mismo color.
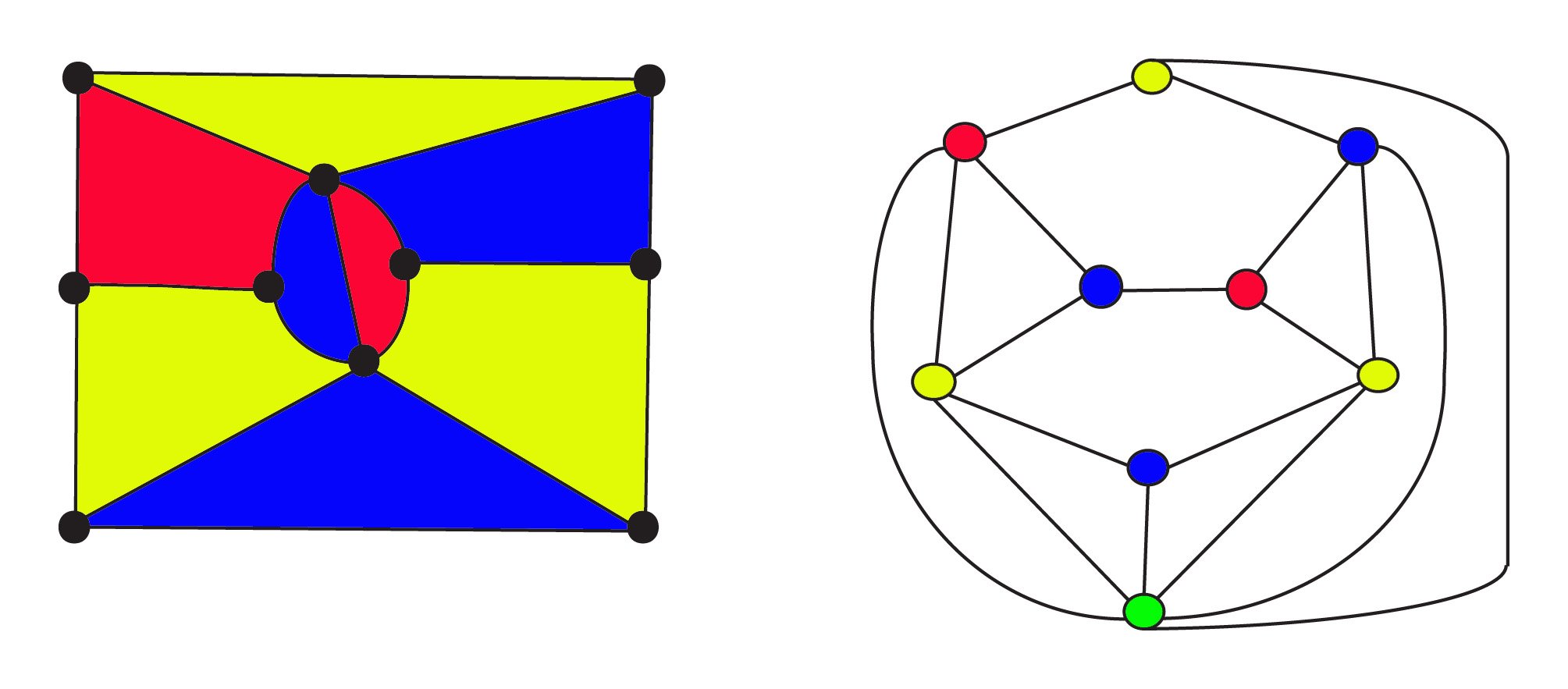
El 3 de color mapa de la izquierda tiene$8$ regiones $10$ vértices y $17$ bordes. Su grafo dual en laderecho tiene $9$ regiones $9$ vértices y $17$ bordes donde thevertices son de color de la misma como las zonas del mapa. El greenvertex en la parte inferior del gráfico representa el área externa infinita para el mapa. Tanto el mapa original como su doble fórmula obedecen a Euler para redes f f + v – e = 1 or o, \\text{regiones} +\text{vértices} – \ text{aristas} = 1.. La relación de dualidad es simétrica: el dual del dual será el grafo original, donde se intercambian regiones y vértices.
Durante la primera mitad del siglo XX, los matemáticos se centraron en modificar este tipo de técnicas para reducir los mapas complicados a casos especiales que pudieran identificarse y clasificarse, para investigar sus propiedades particulares y desarrollar la idea de un conjunto mínimo de configuraciones de mapas que pudieran probarse.
En primera instancia, se pensó que el conjunto contenía casi 9.000 miembros,lo que era una tarea enorme, por lo que los matemáticos recurrieron a técnicas informáticas para escribir algoritmos que pudieran hacer las pruebas para ellos. Los algoritmos utilizaron versiones modificadas de la idea original de cadenas de Kempe junto con otras técnicas para reducir el número de miembros del conjunto mínimo.
Después de colaborar con John Koch en el problema de la reducción, en 1976 en la Universidad de Illinois, Kenneth Appeland Wolfgang Haken finalmente redujo el problema de prueba a un conjunto no evitable con 1936 configuraciones, y se logró una solución completa a la Conjetura de Cuatro Colores. Este problema de comprobar la reducibilidad de los mapas uno por uno se comprobó con diferentes programas y diferentes ordenadores. Su prueba mostró que no puede existir al menos un mapa con el menor número posible de regiones que requieran cinco colores.
Desde la primera prueba, se han encontrado algoritmos más eficientes para mapas de 4 colores y para 1994, el inevitable conjunto de configuraciones se había reducido a 633.
¿Una ‘Prueba’ Realizada en un Ordenador es una Prueba Adecuada?
Debido a que la prueba se hizo con la ayuda de una computadora, hubo una protesta inmediata. Muchos matemáticos y filósofos afirmaban que la prueba no era legítima. Algunos dijeron que las pruebas solo deberían ser «probadas» por personas, no por máquinas, mientras que otros, de una mente más práctica, cuestionaron la fiabilidad de los algoritmos y la capacidad de las máquinas para llevarlas a cabo sin error.Sin embargo, muchas de las pruebas escritas por matemáticos han resultado ser defectuosas, por lo que el argumento sobre la fiabilidad parece vacío.Independientemente de las opiniones expresadas, la situación suscitó un debate serio sobre la naturaleza de la prueba, que aún continúa en la actualidad.
Para notas pedagógicas:
Use la pestaña notas en la parte superior de este artículo o haga clic aquí .
Notas
- Más detalles de este y otros procedimientos que se encuentran en esta sección se pueden ver en el libro de Robin Wilson Four Colours Sufficient .
- Los nudos pueden ser zurdos o diestros, y hoy en día existen importantes aplicaciones de esta propiedad en química, farmacia,biología y física. (Ver Notas Pedagógicas)
- Lleva el nombre de William Rowan Hamilton (1805-1865). Una trayectoria hamiltoniana en un grafo visita cada vértice exactamente una vez. Un ciclo hamiltoniano (o circuito) es una ruta que visita cada vértice exactamente una vez y regresa al vértice inicial.(Ver Notas Pedagógicas)
- El libro de Imre Lakatos, Pruebas y Refutaciones tiene una discusión y crítica del procedimiento de Cauchy (páginas 6-12), y mucho más sobre la historia del Teorema de Euler.
- La idea de dualidad surgió en los siglos XVI y XVII con desarrollos en geometría proyectiva. Matemáticos como Pascal Ydesargues descubrieron que se podían encontrar nuevos teoremas intercambiando los términos «punto» y «línea» en descripciones de ciertas configuraciones geométricas. Un ejemplo es en poliedros regulares, donde los vértices de uno corresponden a las caras del otro. Así que el dualde un tetraedro es otro tetraedro, y el dual de un cubo es un octaedro. El dual del dual es el poliedro original.
El mejor libro popular y fácil de leer sobre el tema de los Cuatro colores es:
Wilson, R. (2003)
Cuatro colores son suficientes.Londres. Penguin Books.
Para una historia más detallada y técnica, el libro de referencia estándar es:
Biggs, N.; Lloyd, E. &Wilson, R. (1986) (1998)
Teoría de grafos,1736-1936
Oxford. Oxford University Press.
Este nos pone al día, con fundaciones y filosofía más recientes.Fritsch, R and Fritsch, G (2000)The Four Color Theorem: History,Topological Foundations, and Idea of Proof Nueva York. Springer-Verlag.
Casi ningún libro de historia general tiene mucho sobre el tema, pero el último capítulo de Katz llamado «Computadoras y Aplicaciones» tiene una sección sobre la Teoría de Grafos, y el Teorema de los Cuatro Colores se menciona dos veces.
Polya G. Cómo resolverlo.Este es el libro clásico sobre la resolución de problemas. Ha habido muchas ediciones de este libro desde que apareció por primera vez en la década de 1950 y todavía está fácilmente disponible. Curiosamente, en ediciones recientes se ha introducido el subtítulo «Un nuevo aspecto del Método Matemático».Lakatos, I. (1976) Proofs andRefutations: The Logic of Mathematical Discovery.Cambridge. C. U. P.
Este es otro libro importante que condujo a la investigación en la Resolución de problemas e Investigaciones en la década de 1970. Comienza como una discusión en el aula entre un profesor y un grupo de estudiantes sobre la prueba de la fórmula de Euler, y se extiende a través de las ideas,objeciones y posibilidades que en realidad fueron discutidas por los matemáticos y científicos en el siglo XIX. Plantea algunos de los temas más importantes sobre la resolución de problemas de enseñanza y aprendizaje y sobre métodos matemáticos y pruebas.
Referencias relacionadas
He tenido un pequeño libro sobre Juegos de cuerdas durante algún tiempo. Cuando estaba en la escuela, se llamaba La cuna del gato, y la tocábamos en nuestro amanecer.
Recientemente, una revista francesa ha publicado un artículo sobre la «álgebra» de las figuras de cuerda! Si vas a Amazon, encontrarás un libro de Ann Swain y Michael Taylor llamado Finger Strings: A Book of Cats Cunas y figuras de cuerdas que será publicado por Floris Books en septiembre de 2008. Hay unas 80 figuras descritas con colores diagrams.It está encuadernado en espiral, por lo que permanecerá abierto mientras sigues las instrucciones. ¡También viene con un par de lazos de cuerda!
Para los expertos en nudos, el AshleyBook of Knots es un clásico para cualquier persona interesada en los nudos de diferentes tipos de nudos y sus usos. Amazon tiene varias ediciones disponibles a diferentes precios.
Enlaces web
Para obtener una visión general y enlaces a muchas personas y temas, el sitio web de Actutor es
Y, por supuesto, las biografías de MacTutor de los involucrados en el desarrollo de todos los diferentes aspectos matemáticos se pueden encontrar en el Índice de Biografías de MacTutor.
El Teorema de los Cuatro Colores y Tres Pruebas. Para lo matemáticamentepersistente, el siguiente sitio web tiene un nuevo enfoque intrigante para abordar el problema de construir un nuevo algoritmo para resolver el problema, y tratar de reducir la dependencia de una computadora.http://www.emu.edu.tr/~cahit/the%20four%20color%20theorem%20—%20three%20proofs.htm
Para la Teoría de grafos, Wikipedia ofrece una buena visión general, y puedes esquivar las cosas realmente técnicas. Muestra los tipos de aplicaciones modernas de esta área de las matemáticas. Si vas a Grafocolor y haces clic en el Teorema de los Cuatro colores, encontrarás mucha más información.
Una historia interesante y no demasiado técnica de la Teoría de Nudos: cómo una idea de la Física de Kelvin regresa hoy a la Teoría Atómica.
La Asociación de Profesores de Matemáticas tiene carteles de Diseño de Nudos Celtas. Vaya a su sitio web y navegue por la lista alfabética de recursos.
¡Descubre todo sobre los nudos en el Atlas de nudos! Si no eres un experto, simplemente disfruta de la variedad y complejidad de la base de datos «en el espíritu de wiki»
Más artístico y colorido, pero no menos matemático es el sitio de Knot Plot.
Para aquellos que quieran algunas de las cosas originales y el detalle histórico, vaya a la Historia de la Teoría de nudos en: