Regression til middelværdien er et almindeligt statistisk fænomen, der kan vildlede os, når vi observerer verden. At lære at genkende, når regression til middelværdien er i spil, kan hjælpe os med at undgå fejlfortolkning af data og se mønstre, der ikke findes.

***

det er vigtigt at minimere tilfælde af dårlig dømmekraft og adressere de svage punkter i vores ræsonnement. At lære om regression til gennemsnittet kan hjælpe os.nobelprisvindende psykolog Daniel Kahneman skrev en bog om fordomme, der overskygger vores ræsonnement og fordrejer vores opfattelse af virkeligheden. Det viser sig, at der er et helt sæt logiske fejl, som vi begår, fordi vores intuition og hjerner ikke håndterer enkle statistikker. En af de fejl, han undersøger i at tænke hurtigt og langsomt, er den berygtede regression mod gennemsnittet.begrebet regression til middelværdien blev først udarbejdet af Sir Francis Galton. Reglen går det, i enhver serie med komplekse fænomener, der er afhængige af mange variabler, hvor chance er involveret, ekstreme resultater har tendens til at blive fulgt af mere moderate.

Ved at søge visdom tilbyder Peter Bevelin eksemplet med John, der var utilfreds med nye medarbejderes præstationer, så han satte dem i et færdighedsforbedrende program, hvor han målte medarbejdernes færdigheder:

deres score er nu højere end de var på den første test. Johns konklusion: “det dygtighedsforbedrende program forårsagede forbedringen af færdighederne.”Dette er ikke nødvendigvis sandt. Deres højere score kan være resultatet af regression til gennemsnittet. Da disse personer blev målt som værende i den lave ende af færdighedsskalaen, ville de have vist en forbedring, selvom de ikke havde taget det færdighedsforbedrende program. Og der kan være mange grunde til deres tidligere præstationer — stress, træthed, sygdom, distraktion osv. Deres sande evne har måske ikke ændret sig.

vores præstation varierer altid omkring nogle gennemsnitlige sande præstationer. Ekstrem ydeevne har tendens til at blive mindre ekstrem næste gang. Hvorfor? Testmålinger kan aldrig være nøjagtige. Alle målinger består af en sand del og en tilfældig fejldel. Når målingerne er ekstreme, er de sandsynligvis delvis forårsaget af en tilfældighed. Chance vil sandsynligvis bidrage mindre på anden gang vi måler ydeevne.

Hvis vi skifter fra en måde at gøre noget på til en anden, blot fordi vi ikke lykkes, er det meget sandsynligt, at vi gør det bedre næste gang, selvom den nye måde at gøre noget på er lige eller værre.

Dette er en af grundene til, at det er farligt at ekstrapolere fra små prøvestørrelser, da dataene muligvis ikke er repræsentative for distributionen. Det er også grunden til, at James March hævder, at jo længere nogen forbliver i deres job, “jo mindre er den sandsynlige forskel mellem den observerede præstationsrekord og den faktiske evne.”Alt kan ske på kort sigt, især i enhver indsats, der involverer en kombination af dygtighed og held. (Forholdet mellem dygtighed og held påvirker også regression til gennemsnittet.)

Regression til gennemsnittet

virkningerne af regression til gennemsnittet kan ofte observeres i sport, hvor effekten forårsager masser af uberettigede spekulationer.

i tænkning hurtigt og langsomt minder Kahneman om at se Mænds skihopp, en disciplin, hvor slutresultatet er en kombination af to separate Spring. Kahneman var opmærksom på regressionen til gennemsnittet og blev forskrækket over at høre kommentatorens forudsigelser om det andet spring. Han skriver:

Norge havde et godt første spring; han vil være anspændt i håb om at beskytte sin føring og vil sandsynligvis gøre det værre” eller “Sverige havde et dårligt første spring, og nu ved han, at han ikke har noget at tabe og vil være afslappet, hvilket skulle hjælpe ham med at gøre det bedre.

Kahneman påpeger, at kommentatoren havde bemærket regressionen til gennemsnittet og kom med en historie, for hvilken der ikke var nogen årsagsbevis (se narrativ fejlslutning). Dette betyder ikke, at hans historie ikke kunne være sand. Måske, hvis vi målte hjertefrekvenserne før hvert spring, ville vi se, at de er mere afslappede, hvis det første spring var dårligt. Det er dog ikke meningen. Pointen er, at regression til gennemsnittet sker, når held spiller en rolle, som det gjorde i resultatet af det første spring.

lektionen fra sport gælder for enhver aktivitet, hvor chance spiller en rolle. Vi vedhæfter ofte forklaringer på vores indflydelse på en bestemt proces til fremskridt eller mangel på det.

i virkeligheden er videnskaben om ydeevne kompleks, situationsafhængig, og ofte er meget af det, vi mener er inden for vores kontrol, virkelig tilfældigt.

i tilfælde af skihop vil en stærk vind mod jumperen føre til, at selv den bedste atlet viser middelmådige resultater. Tilsvarende kan en stærk vind-og skiforhold til fordel for en middelmådig jumper føre til en betydelig, men en midlertidig bump i hans resultater. Disse effekter forsvinder dog, når betingelserne ændres, og resultaterne vil vende tilbage til det normale.

dette kan have alvorlige konsekvenser for coaching og performance tracking. Regressionsreglerne antyder, at når vi vurderer præstationer eller ansættelse, vi skal stole på track records mere end resultater af specifikke situationer. Ellers er vi tilbøjelige til at blive skuffede.da Kahneman holdt et foredrag for det israelske luftvåben om psykologien ved effektiv træning, delte en af officererne sin oplevelse af, at udvidelse af ros til hans underordnede førte til dårligere præstationer, mens skæld førte til en forbedring af efterfølgende bestræbelser. Som en konsekvens, han var vokset til at være generøs med negativ feedback og var blevet temmelig forsigtig med at give for meget ros.

Kahneman opdagede straks, at det var regression til gennemsnittet på arbejdspladsen. Han illustrerede misforståelsen ved en simpel øvelse, du måske vil prøve dig selv. Han tegnede en cirkel på en tavle og bad derefter officererne en efter en om at kaste et stykke kridt i midten af cirklen med ryggen mod tavlen. Derefter gentog han eksperimentet og registrerede hver officers præstation i første og andet forsøg.

naturligvis havde de, der klarede sig utroligt godt i første forsøg, en tendens til at gøre det værre i deres andet forsøg og omvendt. Fejlen blev straks klar: ændringen i ydeevne forekommer naturligt. Det er igen ikke at sige, at feedback slet ikke betyder noget – måske gør det det, men officeren havde ingen beviser for at konkludere, at det gjorde det.

den ufuldkomne korrelation og Chance

på dette tidspunkt undrer du dig måske over, hvorfor regressionen til gennemsnittet sker, og hvordan vi kan sikre os, at vi er opmærksomme på det, når det sker.

for at forstå regression til middelværdien skal vi først forstå korrelation.

korrelationskoefficienten mellem to mål, der varierer mellem -1 og 1, er et mål for den relative vægt af de faktorer, de deler. For eksempel, to fænomener med få faktorer, der deles, såsom forbrug af flaskevand versus selvmordsrate, skal have en korrelationskoefficient på tæt på 0. Det vil sige, hvis vi kiggede på alle lande i verden og planlagde selvmordsrater i et bestemt år mod forbrug af flaskevand pr.

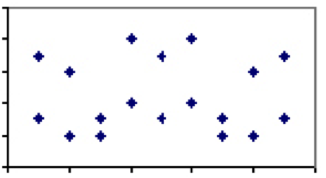
tværtimod er der foranstaltninger, der udelukkende er afhængige af den samme faktor. Et godt eksempel på dette er temperatur. Den eneste faktor, der bestemmer temperaturen – molekylernes hastighed — deles af alle skalaer, derfor vil hver grad i Celsius have nøjagtigt en tilsvarende værdi i Fahrenheit. Derfor vil temperaturen i Celsius og Fahrenheit have en korrelationskoefficient på 1, og plottet vil være en lige linje.

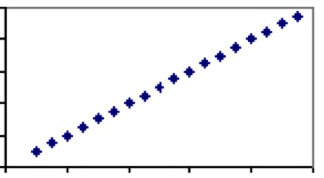
Der er få, hvis nogen fænomener i humanvidenskab, der har en korrelationskoefficient på 1. Der er dog masser, hvor foreningen er svag til moderat, og der er en vis forklarende kraft mellem de to fænomener. Overvej sammenhængen mellem højde og vægt, som ville lande et sted mellem 0 og 1. Mens stort set hver tre-årig vil være lettere og kortere end enhver voksen mand, ikke alle voksne mænd eller tre-årige i samme højde vejer det samme.

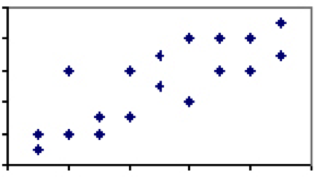
denne variation og den tilsvarende lavere grad af korrelation indebærer, at mens højden generelt er en god forudsigelse, er der klart andre faktorer end højden ved spil. Når sammenhængen mellem to mål er mindre end perfekt, skal vi passe på virkningerne af regression til gennemsnittet.

Kahneman observerede en generel regel: når sammenhængen mellem to scoringer er ufuldkommen, vil der være regression til gennemsnittet.

dette kan i første omgang virke forvirrende og ikke meget intuitivt, men graden af regression til gennemsnittet er direkte relateret til graden af korrelation af variablerne. Denne effekt kan illustreres med et simpelt eksempel.

Antag, at du er på fest og spørg, hvorfor det er, at meget intelligente kvinder har tendens til at gifte sig med mænd, der er mindre intelligente end de er. De fleste mennesker, selv dem med en vis træning i statistik, vil hurtigt hoppe ind med en række årsagsforklaringer lige fra undgåelse af konkurrence til frygt for ensomhed, som disse kvinder står over for. Et emne med sådan kontrovers vil sandsynligvis skabe en stor debat.

hvad nu, hvis vi spurgte, hvorfor sammenhængen mellem ægtefællernes intelligensresultater er mindre end perfekt? Dette spørgsmål er næppe så interessant, og der er lidt at gætte – vi ved alle, at dette er sandt. Paradokset ligger i, at de to spørgsmål tilfældigvis er algebraisk ækvivalente. Kahneman forklarer:

Hvis sammenhængen mellem ægtefællernes intelligens er mindre end perfekt (og hvis mænd og kvinder i gennemsnit ikke adskiller sig i intelligens), så er det en matematisk uundgåelighed, at meget intelligente kvinder vil blive gift med ægtemænd, der i gennemsnit er mindre intelligente end de er (og omvendt selvfølgelig). Den observerede regression til gennemsnittet kan ikke være mere interessant eller mere forklarlig end den ufuldkomne korrelation.

Hvis man antager, at korrelationen er ufuldkommen, er chancerne for, at to partnere repræsenterer de øverste 1% med hensyn til enhver egenskab, langt mindre end en partner, der repræsenterer de øverste 1% og den anden – de nederste 99%.

årsag, virkning og behandling

Vi bør være særligt forsigtige med regressionen til det gennemsnitlige fænomen, når vi forsøger at etablere årsagssammenhæng mellem to faktorer. Når korrelation er ufuldkommen, vil det bedste altid synes at blive værre, og det værste ser ud til at blive bedre over tid, uanset yderligere behandling. Dette er noget, som de generelle medier og nogle gange endda uddannede forskere ikke genkender.

overvej eksemplet Kahneman giver:

deprimerede børn behandlet med en energidrik forbedres betydeligt over en tre måneders periode. Jeg lavede denne avisoverskrift, men det faktum, det rapporterer, er sandt: hvis du behandlede en gruppe deprimerede børn i nogen tid med en energidrik, ville de vise en klinisk signifikant forbedring. Det er også tilfældet, at deprimerede børn, der bruger lidt tid på at stå på hovedet eller kramme en kat i tyve minutter om dagen, også viser forbedring.

Når man støder på sådanne overskrifter, er det meget fristende at springe til den konklusion, at energidrikke, stående på hovedet eller kramme katte alle er perfekt levedygtige kur mod depression. Disse tilfælde belyser imidlertid igen regressionen til gennemsnittet:

deprimerede børn er en ekstrem gruppe, de er mere deprimerede end de fleste andre børn—og ekstreme grupper regresserer til gennemsnittet over tid. Sammenhængen mellem depressionsresultater ved successive testbegivenheder er mindre end perfekt, så der vil være regression til gennemsnittet: deprimerede børn bliver noget bedre over tid, selvom de ikke krammer katte og ikke Drikker Red Bull.

vi tilskriver ofte fejlagtigt en bestemt politik eller behandling som årsag til en effekt, når ændringen i de ekstreme grupper ville være sket alligevel. Dette udgør et grundlæggende problem: Hvordan kan vi vide, om virkningerne er reelle eller blot på grund af variabilitet?

heldigvis er der en måde at fortælle mellem en reel forbedring og regression til gennemsnittet. Det er indførelsen af den såkaldte kontrolgruppe, som forventes at blive bedre ved regression alene. Formålet med forskningen er at afgøre, om den behandlede gruppe forbedrer sig mere, end regression kan forklare.

i virkelige situationer med præstationer for specifikke individer eller hold, hvor det eneste reelle benchmark er den tidligere præstation, og ingen kontrolgruppe kan introduceres, kan virkningerne af regression være vanskelige, hvis ikke umulige at adskille. Vi kan sammenligne med branchens gennemsnit, jævnaldrende i kohortegruppen eller historiske forbedringshastigheder, men ingen af disse er perfekte mål.

***

heldigvis er bevidstheden om regressionen til selve middelfænomenet allerede et godt første skridt i retning af en mere omhyggelig tilgang til forståelse af held og ydeevne.

hvis der er noget at lære fra regressionen til gennemsnittet, er det vigtigheden af track records snarere end at stole på engangs succeshistorier. Jeg håber, at næste gang du støder på en ekstrem kvalitet, der delvis styres af en tilfældighed, vil du indse, at virkningerne sandsynligvis vil regressere over tid og vil justere dine forventninger i overensstemmelse hermed.

Hvad skal du læse næste

• Opgrader din tænkning med 113 mentale modeller forklaret.
• Læs om andet niveau tænkning, så du kan undgå negative konsekvenser.