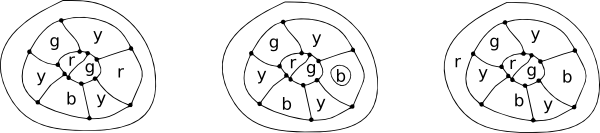
De fire farve sætning
de fire farve formodninger blev først angivet lidt over 150 yearsago, og endelig bevist endegyldigt i 1976. Det er et fremragende eksempel på, hvordan gamle ideer kombineres med nye opdagelser og teknikker inden for forskellige matematikområder for at give nye tilgange til et problem. Det er også et eksempel på, hvordan et tilsyneladende enkelt problem blev anset for at være ‘løst’, men derefter blev merekompleks, og det er det første spektakulære eksempel, hvor en computer var involveret i at bevise en matematisk sætning.
I begyndelsen
formodningen om, at ethvert kort kun kunne farves ved hjælp af fire farver, dukkede først op i et brev fraaugustus De Morgan (1806-1871), første professor i matematik ved Det Nye University College London, til sin ven Vilhelm Rodanhamilton (1805-1865) den berømte irske matematiker i 1852. Det havde været foreslået De Morgan af en af hans studerende, FrederikGuthrie, på vegne af sin ældre bror Francis (som senere blev professor i matematik ved Universitetet i Kapstaden).


Augustus De Morgan (1807-1871) Ogvilliam røn Hamilton (1805-1865)
problemet, så simpelthen beskrevet, men så fristende vanskeligtat bevise, fangede fantasien hos mange matematikere påtid. I slutningen af 1860 ‘ erne tog de Morgan endda problemet og hansbevis til Amerika, hvor blandt andet Benjamin Peirce (1809-1880) afberømt matematiker og astronom, blev interesseret i det som væk for at udvikle sine logiske metoder.
De Morgan brugte det faktum, at i et kort med fire regioner, hverrører de andre tre, en af dem er helt lukket afandre. Da han ikke kunne finde en måde at bevise dette på, brugte han detsom et aksiom , grundlaget forhans bevis.
en kopi af de Morgans originalsketch i sit brev til Hamilton og et simpelt firfarvekort.
i 1878 Arthur Cayley (1821-1895) på et møde i Londonmatematisk samfund spurgte, om nogen havde fundet en løsning forDe Morgans oprindelige spørgsmål, men selv om der havde været nogleinteresse, havde ingen gjort nogen væsentlige fremskridt. Cayley blev interesseret i problemet og offentliggjorde i 1879 et kort papir om farvningen af kort, hvor han forklarede nogle af vanskelighederne med at forsøge et bevis og gav nogle vigtige bidrag til den måde, problemet blev nærmet sig. Hans spørgsmål er, ‘ hvis et bestemt kort allerede med succes er farvet med fire farver,og vi tilføjer et andet område, kan vi stadig beholde den samme farve?’begyndte en anden linje af spørgsmålet, som førte til anvendelsen af matematikinduktion til problemet.

Arthur Cayley (1821-1895)
Arthur Cayley viste, at hvis firefarver allerede var blevet brugt til at farve et kort, og en ny region blev tilføjet, var det ikke altid muligt at beholde originalfarven.
ovenfor er alle fire farver blevet brugt på det originale kort, og ny region er tegnet for at omgive det. I dette tilfælde ændres en rød region til blå, så rød kan bruges på den nye omgivelserregion.
Cayley bemærkede også, at det var muligt at løse en version afproblemet ved at begrænse den måde, grænserne mødtes på. For eksempel, kort, hvor kun tre lande mødtes, har tre kanter, der mødes i averteks. Disse kaldes ‘kubiske kort’, og de kort, der bruges ifølgende diskussion, er alle kubiske kort. Også, hvis et kort kan værefarvet med fire farver, vises kun tre farver på grænsen.
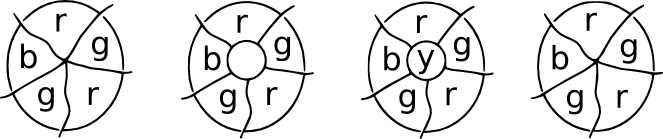
Patch demonstration. Forestil dig, at et sted på et kort mødes en række lande på et tidspunkt. Læg nu en patch over mødestedet, og alle de nye mødesteder vil have tre grænser, der stammer fra dem. Disse er kubiske kort, og en fjerde farve kan bruges til den centrale region. Ved fjernelse af plasteret kan vi vende tilbage til den oprindelige farve.
nogle gamle teknikker, nye forhold og flere problemer!
for at følge udviklingen i problemet skal viundersøg kort nogle af de ideer, procedurer og teknikkerat matematikere udviklede i deres forsøg på at løse det.
de eneste fem naboer formodninger
‘Hvis du ikke kan løse aparticular problem, finde en lettere, som du kan løse.'(Polya. Sådan løses det)
‘hvert kort har mindst et land med fem eller færre naboer.’
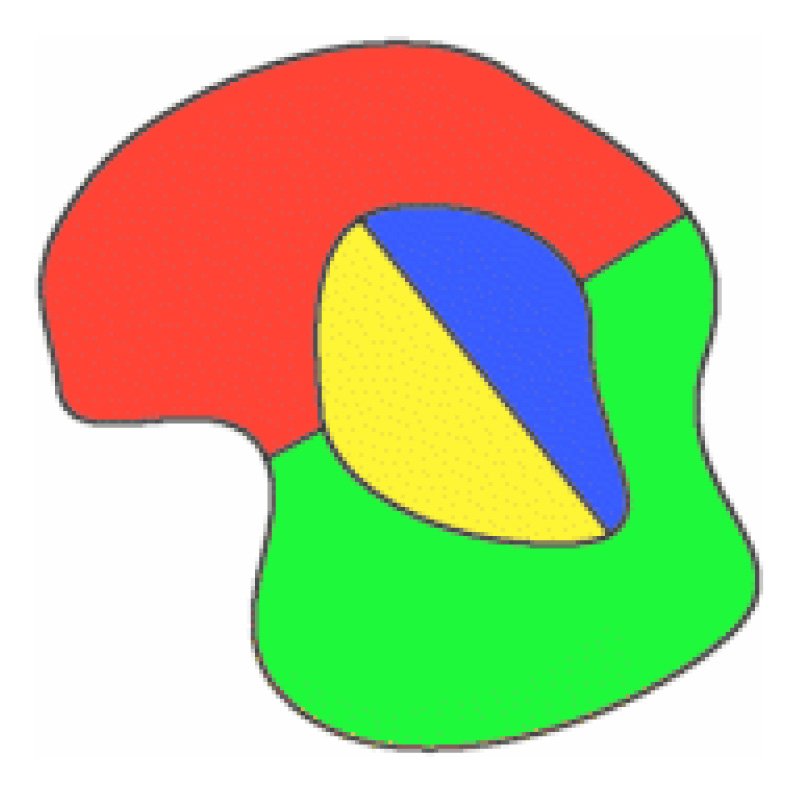
Forestil dig et kort over en ø omgivet af havet. I farvningen af øens lande tæller vi havet som enregion. Nogle lande kan kun have to grænser (en digon), somethree (som i en trekant), nogle Fire (en firkant) og nogle fem (apentagon) eller mere.
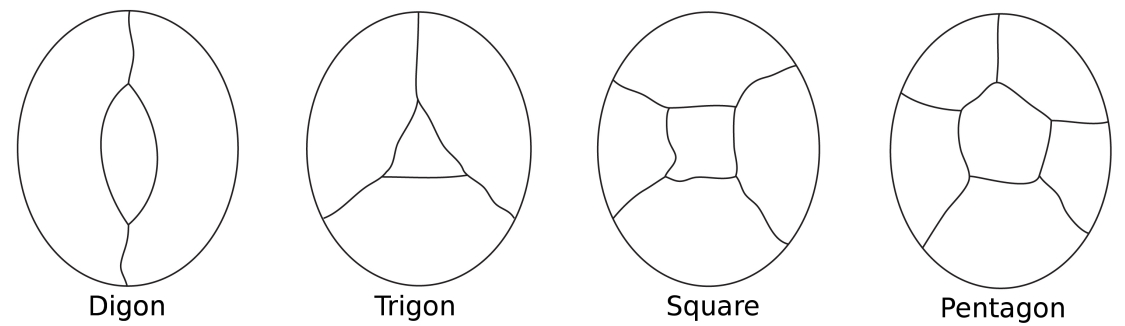
den enkleste muligekonfigurationer for omkring en central region.
Bemærk at i alle disse konfigurationer har hver node kun trekanter.
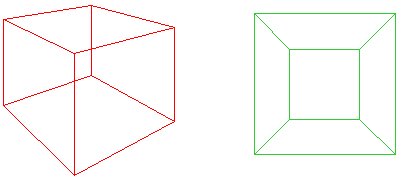
i 1813 blev Eulers formel for polyhedra tilpasset til to dimensioner af Augustin Cauchy (1759-1857) ved at projicere polyhedronen på et plan og således danne nettet af fast stof. På denne måde blev formlen $F + v – E = 1$, fordicauchy tællede ikke den ‘udenfor’ region af nettet.

Augustin Cauchy (1759-1857)
forestil dig at klemme den røde terning ned på et plan, så dens base åbnes ud for at danne ydersiden af det grønne Net. Cauchys ide var at skære et ansigt afcube, så for en plan polygon, $f + v – e = 1$. Alternativt, hvis’ ydersiden ‘ af nettet betragtes som et ansigt med infinitearea, så har vi stadig $f + v – e = 2$
Vi kan antage, at der er mindst tre grænselinjer (kanter), der kommer ud fra hvert mødested (hjørner).
beviset for, at kortet har mindst et land omgivet affem eller færre naboer, går ud af modsigelse. Hvis dette fører til en absurditet, har vi et bevis.
sæt nu disse værdier i Eulers formel: $$f + v – E = 2$$ ogvi har $$1/3(e) + 2/3 (e) – E$$ hvilket er nul!
dette er absurditeten, så vores oprindelige antagelse var falsk.Det betyder, at der skal være mindst et land med fem eller færre naboer!
minimale kriminelle!
en anden måde at tackle problemet med fire farver på er at antage, at det er falskt, og se, hvor dette fører. Antag, at der er kort, der har brug forfem farver eller mere, og vi vælger kortene med det mindst mulige antal lande. Disse kort kaldes minimale modeksempler ellerminimale kriminelle !
så det betyder,at en minimal kriminel ikke kan farves med fire farver, men ethvert kort med færre lande kan farves med fire farver. Hvis vi kan vise, at minimale kriminelle ikke kan eksistere, kan vi muligvis gøre nogle fremskridt.
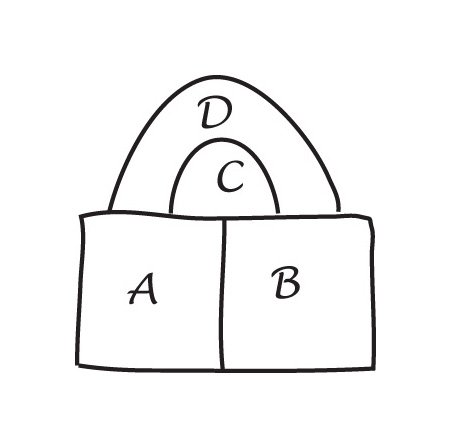
for eksempel kan vi vise, at en minimal kriminel ikke kan indeholdeen digon.
fra det oprindelige kort skal du fjerne en grænse fra digon ogvi får et nyt kort med færre lande. Dette kort kan farves med fire farver (fra vores antagelse). Vi farver derefter dette nye kort (vi har kun brug for to farver). Nu erstatte grænsen vi fjernet, og re-farve kortet. Vi har brugt tre farver, og da thereis stadig en farve til rådighed, Dette viser, at vores kort kan becoloured med fire farver. Men det er imod vores antagelse, så en minimal kriminel kan ikkeindeholder en digon.
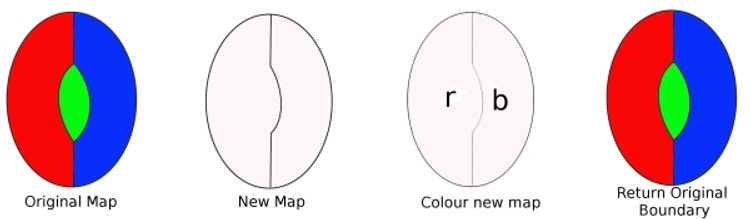
for at vise, at en Minimal Kriminelkan ikke indeholde en region med to kanter (en digon). Antag at der eren minimal kriminel, der indeholder en digon. Fjernelse af en kant betyderkortet indeholder færre regioner. Så dette nye kort kan farves med fire farver. Udskift nu den tabte kant. Da der kun var brug for to farver før, udskiftning af kanten betyder, at vi kan bruge en tredjedel farve, og har stadig en fjerde farve at bruge. Så en minimalkriminel kan farves med fire farver. Derfor kan en minimalkriminel ikke indeholde en digon.
denne procedure kan gentages for at vise, at en minimal kriminelkan ikke indeholde et tresidet land (en trigon), men det går i stykker, når vi prøver teknikken på en firkant, fordi når vi udskifter kvadratet, kan landene ved siden af det godt bruge alle firefarver, så bevisproceduren fejler. Når dette er sket, bliver det indlysende, at det ikke virker for pentagoner osv.
seks farve sætning
en lignende teknik kan anvendes til at vise, at de seks farveteorem er sandt. For det første antager vi, at der ikke er nogen kort, der kan værefarvet med seks farver. Nogle af kortene kan farves medsyv farver, så ved at vælge en af disse (en minimal kriminel), hvis vi kan vise, at det er muligt at farve det med mindre end syvfarver, har vi nået vores mål.
fra beviset for fem naboers sætning er det muligt at fortsætte med at bruge den minimale kriminelle ide for at vise, at ethvert kort kan farves med seksfarver!
fra regioner til knuder, netværk og topologi
i 1879 Alfred Kempe (1849-1922), ved hjælp af teknikker svarende til dem, der er beskrevet ovenfor, startede fra ‘fem naboer ejendom ‘og udviklet en procedure kendt som metoden til’ Kempe kæder ‘ for at finde et bevis på de fire farver sætning. Han offentliggjorde dette bevis iAmerikansk Tidsskrift for Matematik. Han fandt to enklere versioner, der blev offentliggjort i det næste år, og hans bevis stod i ti år, før Percy heave (1861-1955) viste, at der var en vigtig fejl i den bevismetode, som Kempe havde brugt.


Alfred Kempe (1849-1922), PeterGuthrie Tait (1831-1901) og Percy heaved (1861-1955)
i 1880 P. G. Tait (1831-1901) en matematisk fysiker, tilbydeten løsning på problemet. Uafhængigt havde Tait fastslået,at kort, hvor et lige antal grænselinjer mødes på hvert punkt, kunne farves med to farver, skønt dette resultat var dukket op tidligere i Kempe ‘ s papirer.
i løbet af 1876-77 blev Tait kendt for sin undersøgelse ogklassificering af knuder. På det tidspunkt var der en rækkeforskellige teorier om atomernes struktur. Vilhelm Thompson (senere Lord Kelvin 1824-1907) inspireret af eksperimenterne fra den tyske fysiker Hermann von Helmholts (1821-1894) foreslog ateori at atomer blev knyttede rør af ether. Kelvins teori om’ vorteksatomer ‘ blev taget alvorligt i omkring tyve år, og det inspirerede Tait til at foretage en klassificering af knuder. Tait, Thomsonog James Clark Maksvå (1831-1879) opfandt mange topologiske ideerunder deres studier. Kelvins teori var dog grundlæggendeforstyrret og fysikere mistede interessen for Taits arbejde.


Hermann von Helmholts (1821-1879),Lord Kelvin (1824-1907) og James Clark (1831-1879)

Tait begyndte med de måder, hvorpå asingle lukket sløjfe af ledningen kunne knyttes. Han havde ingen systematisk metode i starten og begyndte på en intuitiv måde ved at tage asingle closed loop og eksperimentere med de måder, hvorpå det kunne knyttes. Selvfølgelig måtte ledningen være åben (som ashoelace) derefter knyttede og sluttede sig. Bemærk, at hvis du følger thecord omkring knuden, vil ‘over – under’ krydsninger skifte.Han fortsatte derefter med at eksperimentere med to sløjfer og de måder, hvorpå de kunne knyttes sammen. Vist her er knuder med op til sekskrydsninger for en enkelt sløjfe.
et af resultaterne af Taits undersøgelse var hans Hamiltonian graph formodning.
et kort betragtes som en polyhedron tegnet på en kugle, og det kan derefter projiceres på et plan. Tait foreslog, at ethvert cubicpolyhedralkort har en Hamiltoniancycle . Taits metode fokuserede på kanterne af grafen oghan viste, at en Hamiltonian cyklus kunne producere en fire-farvning af et kort. Det var først i 1946, at Vilhelm Tutte (1917-2002) fandt det første modeksempel på Taits formodning.
Tait og forbindelsen med knuder
Taitinitierede undersøgelsen af snarks i 1880, da han beviste, at fourcolour-sætningen svarede til udsagnet om, at ingen snark erplanar. En plan graf er en, der kan tegnes i flyet Medingen kanter krydser. Det ser ud som om Tait ‘ s ide om ikke-plane graphsmight er kommet fra hans undersøgelse af knuder og Hamiltonian stier .
den første kendte snark var Petersen-grafen opdaget i 1898, og matematikere begyndte at jage efter flere af disse slags grafermen det var først i 1946, at en anden snark blev fundet.
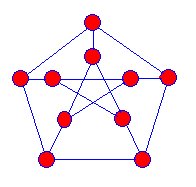 |
SNARKS er fremskrivninger af tredimensionelle grafer på flyet. Der er ingen hjørner, hvor de blå kanter ser ud til at krydsehinanden. Snarks har følgende egenskaber:
|
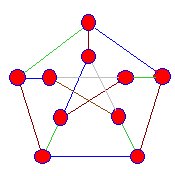 |
kanterne,der møder hjørnerne af denne snark, er farvet blå, grøn og brun, men vi når altid et stadium, hvor denne proceskan ikke fortsættes. |
Julius Peterson (1839-1910)
jagten på thesnark er et digt skrevet af Levis Carroll, og Martin gardnernavngivet disse grafer SNARKS, fordi de var så undvigende.
transformere problemet og finde nye metoder.
selvom han fandt den største fejl i Kempe ‘ s bevismetode i 1890, var han ude af stand til at fortsætte med at bevise sætningen med fire farver, men han gjorde et betydeligt gennembrud og beviste endeligt, at alle kort kunne farves med fem farver.
heave gjort mange vigtige bidrag til problemet,flytte fokus for opmærksomhed fra de områder af et kort, tilgrænserne mellem dem. I 1898 havde han bevist, at hvis antallet af kanter omkring hver region kan deles med 3, kunne regionerne farves med fire farver.
Cauchys bevis på Eulers formel omfattede også ideen om, atethvert net af en polyhedron kan trianguleres ved at tilføje kanter til makenon-trekantede ansigter i trekanter. Han udviklede derefter en procedurehvorved han slettede kanterne en efter en, hvilket viste, at Euler ‘ sformula kunne opretholdes ved hvert trin.
Cauchys bevis for Eulers formel
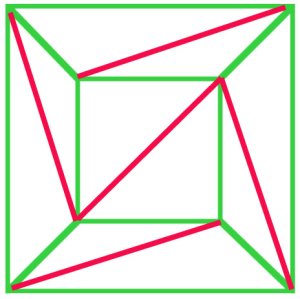
Cauchys 1813-bevis for Eulers formel begyndte med ideen om aprojektion af en polyhedron for at opnå et Plannet. Han videredemonstrerede (a), at ethvert net kunne trianguleres, og hans bevis(b) på Eulers formel blev accepteret på det tidspunkt.
 (a)
|
In principle, every polygonal net can be triangulated. In thisnet of a cube (a), $f + v – e$ is $10 + 8 – 17 = 1$, and Euler’sformula still holds. |
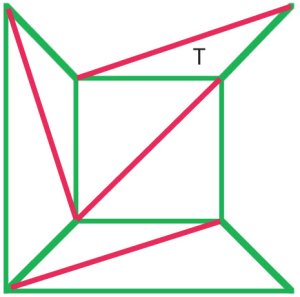 (b)
|
Cauchys argument var at fjerne de ydre kanter fra diagrammet(a) en efter en, og da han nåede et stadium som et i diagram (B)fjernede hele trekanten t og bevarede således Eulers formel. Mangematematikere fra begyndelsen af det nittende århundrede var enige om, at detteproceduren viste et bevis på Eulers formel for allpolyhedra. |
i 1900 vidste matematikere, at en plan graf kan værekonstrueret fra ethvert kort ved hjælp af det magtfulde koncept af dualitet . I det dobbelte er derregioner repræsenteret af hjørner, og to hjørner er forbundet meden kant, hvis regionerne er tilstødende. I disse grafer spørger FourColour-formodningen nu, om grafens hjørner kan farves med 4 farver, så ingen to tilstødende hjørner er den samme farve.
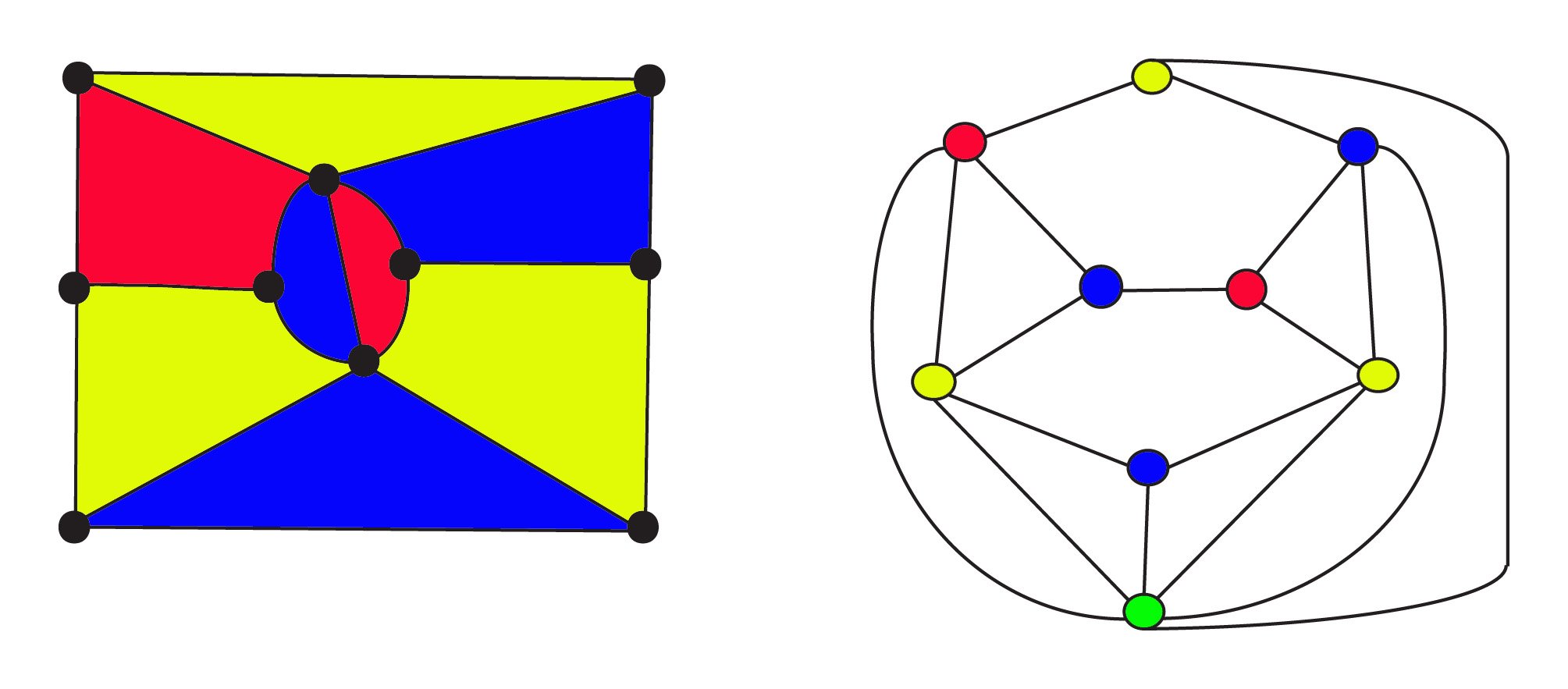
det 3-farvede kort til venstre har$8$ regioner $10$ hjørner og $17$ kanter. Dens dobbelte graf på theright har $ 9 $ regioner $ 9$ hjørner og $ 17 $ kanter, hvor hjørner er farvet det samme som områderne på kortet. Den grønne vinkel i bunden af grafen repræsenterer det uendelige eksterneområde for kortet. Både det originale kort og dets dobbelte adlyd Euler ‘ sformula for netværk $f + v – e = 1$ eller, $\tekst{regioner} +\tekst{hjørner} – \tekst{kanter} = 1$. Dualitetsforholdet ersymmetrisk: Dobbelt af dobbelt vil være den oprindelige graf, hvorregioner og hjørner udveksles.
i løbet af første halvdel af det tyvende århundrede fokuserede matematikere på at ændre denne slags teknikker for at reducerekomplicerede kort til særlige tilfælde, der kunne identificeres og klassificeres, for at undersøge deres særlige egenskaber og udvikle ideen om et minimalt sæt kortkonfigurationer, der kunne testes.
i første omgang blev Sættet anset for at indeholde næsten 9.000 medlemmer, hvilket var en enorm opgave,og så matematikerne vendte sig til computerteknikker til at skrive algoritmer, der kunne gøre dettest for dem. Algoritmerne brugte modificerede versioner af Kempe ‘ s oprindelige ide om kæder sammen med andre teknikker til at reducereantallet af medlemmer af det minimale sæt.efter at have samarbejdet med John Koch om problemet med reducerbarhed, i 1976 ved University of Illinois, Kenneth Appeland Ulfgang Haken reducerede til sidst testproblemet til et ikke-undgåeligt sæt med 1.936 konfigurationer, og en komplet løsning til de fire farver formodninger blev opnået. Dette problem med at kontrollere kortets reducerbarhed en efter en blev dobbeltkontrolleret med forskellige programmer og forskellige computere. Deres bevis viste, at mindst et kort med det mindst mulige antal regioner, der kræver fem farver, ikke kan eksistere.
siden det første bevis er der fundet mere effektive algoritmer til 4-farvekort, og i 1994 var det uundgåelige sæt afkonfigurationer reduceret til 633.
er et’ bevis ‘ udført på en Computer et korrekt bevis?
fordi beviset blev gjort ved hjælp af en computer, var deret øjeblikkeligt skrig. Mange matematikere og filosoffer hævdedeat beviset ikke var legitimt. Nogle sagde, at Bevis kun skulle ‘bevises’ af mennesker, ikke maskiner, mens andre af et mere praktisk sind satte spørgsmålstegn ved pålideligheden af både algoritmerne og maskinernes evne til at udføre dem uden fejl.Imidlertid har mange af de beviser, der er skrevet af matematikere, væretfundet at være defekt, så argumentet om pålidelighed virker tomt.Uanset de udtalelser, der blev udtrykt, frembragte situationen en alvorligdiskussion om arten af bevis, som stadig fortsætteri dag.
til pædagogiske noter:
brug fanen noter øverst i denne artikel, eller klik her .
noter
- flere detaljer om dette og de andre procedurer, der findes i dette afsnit, kan ses i Robin Vilsons bog Fire farver er tilstrækkelige .
- knuder kan være venstrehåndede eller højrehåndede, og i dag er dervigtige anvendelser af denne ejendom inden for kemi, apotek,biologi og fysik. (Se pædagogiske noter)
- opkaldt efter Vilhelm Hamilton (1805-1865). En Hamiltonian sti i en graf besøgerhver toppunkt præcis en gang. En Hamiltonian cyklus (eller kredsløb) er apath som besøger hvert toppunkt nøjagtigt en gang og vender tilbage tilstartende toppunkt.(Se pædagogiske noter)
- bogen af Imre Lakatos, Proofs and Refutations har en diskussion og kritik af Cauchys procedure (side 6 – 12) ogmeget mere om historien om Eulers sætning.
- ideen om dualitet opstod i det 16.og 17. århundrede medudvikling i Projektiv geometri. Matematikere som Pascal andDesargues fandt ud af, at nye sætninger kunne findes ved at udveksle vilkårene ‘punkt’ og ‘linje’ i beskrivelser af visse geometriskekonfigurationer. Et eksempel er i regelmæssig polyhedra, hvorvertices af en svarer til ansigterne på den anden. Så dualof en tetraeder er en anden tetraeder, og den dobbelte af en terning er en oktaeder. Den dobbelte af den dobbelte er originalenpolyhedron.
den allerbedste populære, let at læse bog om de fire Farverteorem er:
Vilson, R. (2003)
Fire farver er tilstrækkelige.
København. Penguin Bøger.
for en mere detaljeret og teknisk historie er standardreferencebogen:
Biggs, N.; Lloyd, E. &Vilson, R. (1986) (1998)
Grafteori, 1736-1936
Oksford. University Press.
Denne bringer os ajour med nyere fundamenter ogfilosofi.
Fritsch, R og Fritsch, G (2000)
De Fire farver sætning: historie,topologiske fundamenter, og ideen om bevis
Ny York. Springer-Verlag.(1998)
Polya G. Sådan løses det.
Dette er den klassiske bog om problemløsning. Der har væretmange udgaver af denne bog siden den først dukkede op i 1950 ‘ erne Ogden er stadig let tilgængelig. Mærkeligt nok har de seneste udgaver væretgivet underteksten ‘et nyt aspekt af matematisk metode’.
Lakatos, I. (1976) beviser ogfutationer: logikken i matematisk opdagelse.
Cambridge. C. U. P.
Dette er en anden vigtig bog, som førte til forskning i problemløsning og undersøgelser i 1970 ‘ erne. Det begynder som en klasserum diskussion mellem en lærer og en gruppe studerende om beviset for Eulers formel og spænder gennem de ideer, indvendinger og muligheder,der faktisk blev diskuteret afmatematikere og forskere i det nittende århundrede. Det rejser nogle af de vigtigste spørgsmål om undervisning og læringproblemløsning og om matematiske metoder og bevis.
relaterede referencer
Jeg har haft en lille bog om Strengespil i nogen tid. Da jeg var i skole, blev det kaldt Cat ‘ s Cradle, og vi spillede det i voresbreak tid.
for nylig har et fransk tidsskrift udgivet et papir om’ algebra ‘ af strengfigurer! Hvis du går til
for knudeeksperter er Knobens Ashleybog en klassiker for alle interesserede ihundredvis af forskellige slags knuder og deres anvendelser.
links
for en generel oversigt og links til mange mennesker og emner, theMacTutor hjemmeside er
og selvfølgelig MacTutor biografier af de involverede iudvikle alle de forskellige matematiske aspekter kan findes på MacTutor biografier indeks.
de fire farver sætning og tre beviser. For den matematiskvedholdende har følgende hjemmeside en spændende ny tilgang tilangribe problemet med at konstruere en ny algoritme til løsning af problemet og binde for at reducere afhængigheden af en computer.http://www.emu.edu.tr/~cahit/the%20four%20color%20theorem%20—%20three%20proofs.htm
for Grafteori giver vi et godt overblik, og du kan springe over de virkelig tekniske ting. Det viser de slags moderneanvendelser af dette område af matematik. Hvis du går til GraphColouring og klikker på de fire farver sætning, så vil du findeen masse mere information.
en interessant og ikke for teknisk historie om Knudeteori – hvordan en ide fra Kelvins fysik vender tilbage til Atomteorieni dag.
Foreningen af lærere i matematik har Celtic Knotdesign plakater. Gå til deres hjemmeside og gennemse den alfabetiskeliste over ressourcer.
Find ud af alt om knuder på Knot Atlas! Hvis du ikke er en ekspert-bare nyde mangfoldigheden og kompleksiteten af databasen “i ånden af Viki”
mere kunstnerisk og farverig – men ikke mindre matematisk erknot Plot Site.
for dem, der ønsker nogle af de oprindelige ting og historiskedetaljer gå til historien om knude teori om: