Čtyři Barvy Věta
Čtyři Barvy Domněnkou bylo poprvé uvedeno jen něco přes 150 yearsago, a nakonec přesvědčivě dokázal v roce 1976. Je to vynikající příklad toho, jak se staré myšlenky kombinují s novými objevy a technologiemi v různých oblastech matematiky, aby poskytly nové přístupy k problému. To je také příklad, jak může apparentlysimple problém byl myšlenka být „vyřešeno“, ale pak se stal morecomplex, a to je první nádherný příklad, kde computerwas podílí dokázat matematické věty.
na Začátku
domněnkou, že každá mapa by mohla becoloured pouze pomocí čtyř barev se poprvé objevil v dopise fromAugustus De Morgan (1806-1871), první profesor matematiky na nové University College v Londýně, jeho přítel William RowanHamilton (1805-1865) slavný Irský matematik v roce 1852. To bylo navrhl, De Morgan, jeden z jeho studentů, FrederikGuthrie, jménem jeho starší bratr Francis (který se později becameprofessor matematiky na University of Cape Town).


Augustus De Morgan (1807-1871) andWilliam Rowan Hamilton (1805-1865)
problém, tak jednoduše popsat, ale tak provokativně obtížné dokázat, zachytil představivost mnoha matematiků tehdy. V pozdních 1860s De Morgan dokonce vzal problém a hisproof do Ameriky, kde mimo jiné, Benjamin Peirce (1809-1880) afamous matematik a astronom, se začal zajímat o to, jak se dál rozvíjet jeho logické metody.
De Morgan použil skutečnost, že v mapě se čtyřmi oblastidotýká se ostatních tří, jeden z nich je zcela uzavřen ostatními. Protože nemohl najít způsob, jak to dokázat, použil tojako axiom, základjeho důkaz.
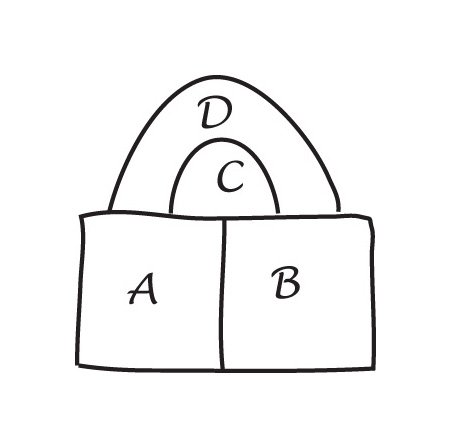
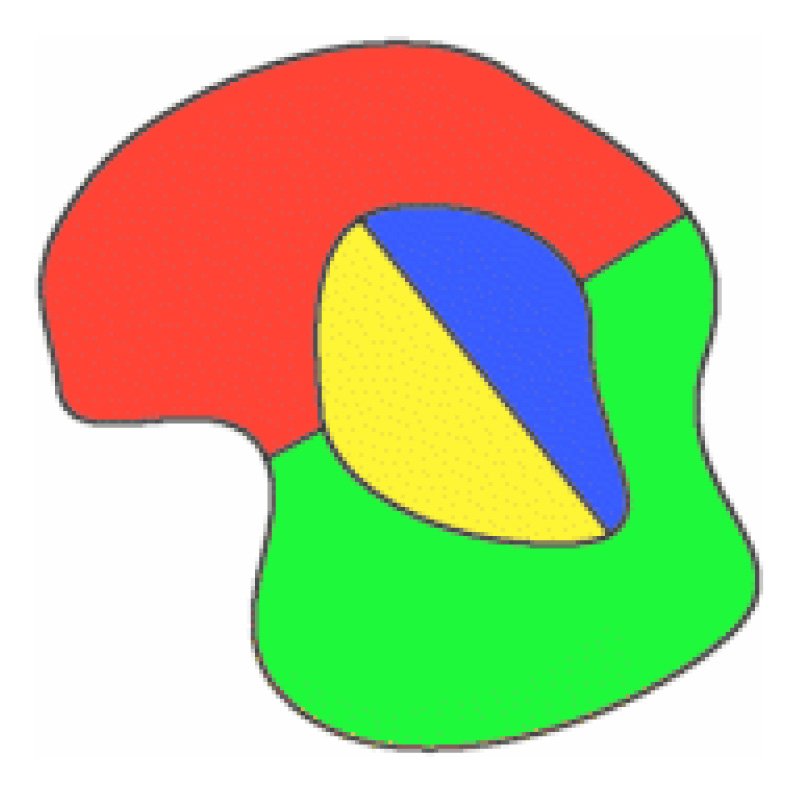
kopie De Morgan originalsketch ve svém dopise Hamilton a jednoduchý čtyř barevných map.
V roce 1878 Arthur Cayley (1821-1895) na zasedání LondonMathematical Společnosti se zeptal, zda měl někdo našel řešení forDe Morgan původní otázku, ale i když tam byl someinterest, nikdo neměl neudělali žádný významný pokrok. Cayley becameinterested v problému a v roce 1879 publikoval krátké papír na vybarvování mapswhere vysvětlil některé problémy při pokusu o proofand některé významné příspěvky k řešení problému wasapproached. Jeho otázka, “ pokud je konkrétní mapa již úspěšně obarvena čtyřmi barvami a přidáme další oblast, můžeme stále zachovat stejné zbarvení?“začala další řada dotazů, která vedla k aplikaci matematické indukce na problém.

Arthur Cayley (1821-1895)
Arthur Cayley ukázal, že pokud fourcolours již byla použita na barevné mapě, a v novém regionu, wasadded, to není vždy možné, aby originalcolouring.
výše, všechny čtyři barvy byly použity na původní mapě, a znovu region je zakreslena obklopit. V tomto případě je červená oblast změněna na modrou, takže červená může být použita na novém okolíregionu.
Cayley také poznamenal, že bylo možné vyřešit verzi problému omezením způsobu, jakým se hranice setkaly. Například mapy, kde se setkaly jen tři země, mají v avertexu tři hrany. Nazývají se „kubické mapy“ a mapy použité v následující diskusi jsou všechny kubické mapy. Také, pokud mapa může býtbarva se čtyřmi barvami, na hranici se objeví pouze tři barvy.
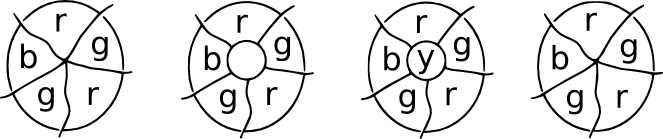
Patch demonstrace. Představte si tona nějakém místě na mapě se v určitém okamžiku setkává řada zemí. Nyní vložte náplast přes místo setkání a všechny nové body setkání budou mít tři hranice vycházející z nich. Jedná se o kubické mapy a čtvrtou barvu lze použít pro centrální oblast. Po odstranění náplasti se můžeme vrátit k původnímu zbarvení.
některé staré techniky, nové podmínky a další problémy!
abychom mohli sledovat vývoj problému, potřebujemekrát prozkoumáme některé myšlenky, postupy a technikyže matematici vyvinuli ve svých pokusech o jeho řešení.
pouze pět sousedů domněnky
‚ Pokud nemůžete vyřešit zvláštní problém, najděte jednodušší, který můžete vyřešit.“(Polja. Jak to vyřešit)
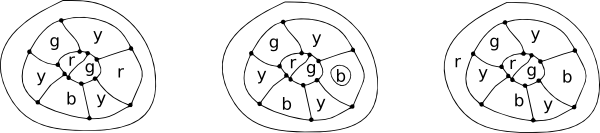
‚ Každá mapa má alespoň jednu zemi s pěti nebo méně sousedy.‘
Představte si mapu ostrova obklopeného mořem. Při zbarvení zemí ostrova počítáme moře jako jeden region. Některé země mohou mít pouze dvě hranice (digon), somethree (jako v trojúhelníku), některé čtyři (čtverec) a některé pět (apentagon) nebo více.
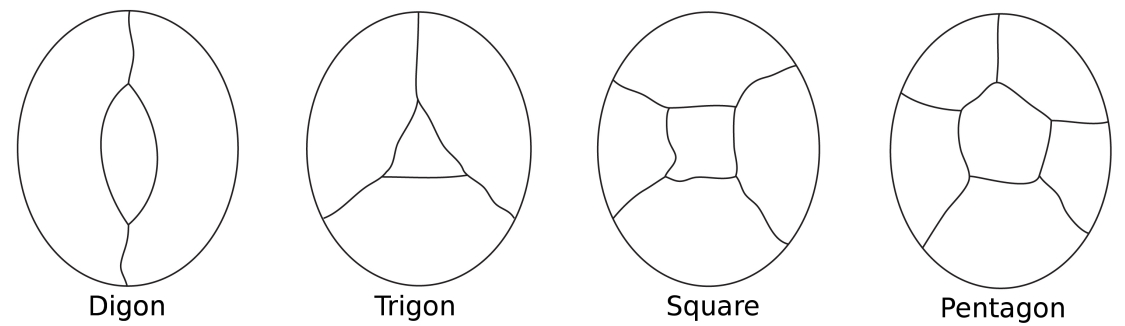
nejjednodušší možnékonfigurace pro okolí centrální oblasti.
Všimněte si, že ve všech těchto konfiguracích má každý uzel pouze tři řádky.
V roce 1813, Eulerův vzorec pro mnohostěny wasadapted pro dva rozměry podle Augustina Cauchyho (1759-1857) byprojecting mnohostěn, na rovině a tvoří tak síť thesolid. Tímto způsobem se vzorec stal $f + v-e = 1$, protožecauchy nepočítal „vnější“ oblast sítě.

Augustin Cauchy (1759-1857)
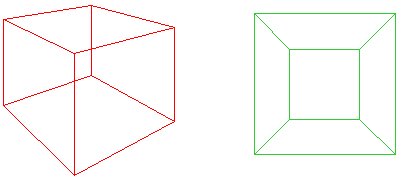
Představte si, drtil červená kostka downonto rovině tak, že jeho základna je otevřen formulář outsideedge zelené čisté. Cauchyho myšlenkou bylo vystřihnout jednu tvářcube, takže pro rovinný mnohoúhelník, $f + v-e = 1$. Případně,pokud „mimo“ síť je považována za tvář s infinitearea, pak stále máme $f + v – e = 2$
předpokládejme, že existují nejméně tři hraniční čáry (hrany), vznikající z každého setkání (vrcholy).
důkaz, že mapa má alespoň jednu zemi obklopenou pěti nebo méně sousedy, je protichůdný. Pokud to vede k absurditě, máme důkaz.
Nyní vložte tyto hodnoty do Eulerova vzorce: $$f + v – e = 2$$ a $$1/3(e) + 2/3(e) – e$$ což je nula!
to je absurdita, takže náš původní předpoklad byl nepravdivý.To znamená, že musí existovat alespoň jedna země s pěti nebo méně sousedy!
minimální zločinci!
dalším způsobem, jak řešit čtyři barevné problém je předpokládat, že isfalse, a uvidíme, kam to vede. Předpokládejme, že existují mapy, které potřebují pět nebo více barev, a vybíráme mapy s nejmenším možným počtem zemí. Tyto mapy se nazývají minimální proti-příklady nebominimální zločinci !
to znamená, že minimální zločinec nemůže být obarven čtyřmi barvami, ale každá mapa s menším počtem zemí může být obarvena čtyřmi barvami. Pokud dokážeme, že minimální zločinci nemohou existovat, pak bychom mohli dosáhnout určitého pokroku.
například můžeme ukázat, že minimální zločinec nemůže obsahovata digon.
Z původní mapy, odnést hranice z digon, a dostat novou mapu s méně zemí. Tato mapa může být vybarvena čtyřmi barvami (z našeho předpokladu). Tuto novou mapu pak obarvíme (potřebujeme pouze dvě barvy). Nyní vyměňte ohraničení, které jsme odstranili, a přebarvte mapu. Použili jsme tři barvy, a protože je k dispozici ještě jedna barva, ukazuje to, že naše mapa může být zbarvena čtyřmi barvami. Ale to je proti našemu předpokladu, takže minimální zločinceobsahují digon.
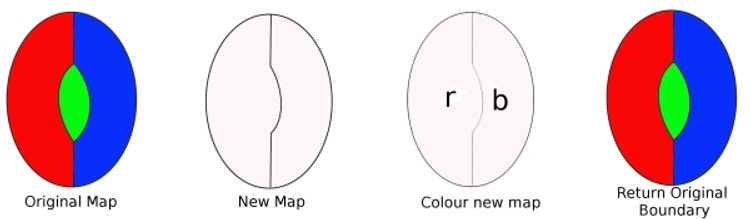
ukázat, že Minimální Criminalcannot obsahují oblasti s dvěma hranami (digon). Předpokládejme, že existujeminimální zločinec, který obsahuje digon. Odstranění okraje prostředkymapa obsahuje méně oblastí. Takže tato nová mapa může být vybarvenase čtyřmi barvami. Nyní vyměňte ztracenou hranu. Vzhledem k tomu, že dříve byly potřeba pouze dvě barvy, výměna okraje znamená, že můžeme použít třetí barvu,a stále máme čtvrtou barvu. Takže minimálníkriminál může být zbarven čtyřmi barvami. Proto minimální zločin nemůže obsahovat digon.
Tento postup může být opakován, aby ukazují, že minimální criminalcannot obsahovat tři-sided země (trigon), ale to se zlomí downwhen jsme zkusit techniku na náměstí, protože když jsme se nahradit thesquare, země, vedle ní může být s využitím všech fourcolours, takže důkaz, že postup selže. Jakmile se to stane, je zřejmé, že to nebude fungovat pro pětiúhelníky a tak dále.
Šest Barevných Věta
podobná technika může být použita, aby ukázal, že šest colourtheorem je pravda. Za prvé, předpokládáme, že neexistují žádné mapy, které by mohly býtbarvy se šesti barvami. Některé mapy mohou být barvené withseven barvy, takže výběr jednoho z nich (minimální trestní), když může ukázat, že je možné barvu s méně než sevencolours, jsme dosáhli našeho cíle.
z důkazu věty o pěti sousedech je možné pomocí minimálního kriminálního nápadu ukázat, že každá mapa může být zbarvena šesti barvami!
Z Regionů Uzlů, Sítí a Topologie
V roce 1879 Alfred Kempe (1849-1922), pomocí techniky podobné jako ty popsané výše, začala se z pěti sousedy majetku a vyvinut postup, známý jako metoda ‚Kempe Řetězce prý důkaz, že Čtyři Barvy Věta. Tento důkaz publikoval vAmerický žurnál matematiky. Našel dva jednodušší versionsthat byly zveřejněny v příštím roce, a jeho důkaz stál za víc jak deset let, než Percy Heawood (1861-1955), ukázal, že byla zásadní chyba v důkazu-metoda, která Kempe měl použít.


Alfred Kempe (1849-1922), PeterGuthrie Tait (1831-1901) a Percy Heawood (1861-1955)
V roce 1880 P. G. Tait (1831-1901) matematický fyzik, offereda řešení problému. Nezávisle, Tait založil thatmaps, kde sudé číslo linky hranice se setkat na každém místě,by mohl být barvené s dvěma barvami, i když i tento výsledek hadappeared dříve v Kempe papíry.
během let 1876-77 se Tait stal známým pro své studium aklasifikace uzlů. V té době bylo řadarůzné teorie o struktuře atomů. William Thompson(Později Lord Kelvin 1824-1907) inspirován experimenty fc Fyzik Hermann von Helmholtz (1821-1894) navrhované atheory, že atomy jsou vázané trubky z éteru. Kelvinova teorie „atomů vortexu“ byla brána vážně asi dvacet let, a to vyžadovalo Tait provést klasifikaci uzlů. Tait, Thomsona James Clark Maxwell (1831-1879) vynalezl mnoho topologických myšlenekběhem studia. Kelvinova teorie však byla zásadněpřipomenuti a fyzici ztratili zájem o Taitovu práci.


Hermann von Helmholtz (1821-1879),Lord Kelvin (1824-1907) a James Clark Maxwell (1831-1879)

Tait začal s způsobů, v němž jednoduchou uzavřenou smyčku šňůry by mohly být vázané. Neměl systematicmethod na začátku, a začal v intuitivním způsobem tím, že jednoduchou uzavřenou smyčku a experimentovat s způsoby, v nichž mohl být vázané. Šňůra musela být samozřejmě otevřená (jako ashoelace), poté svázaná a spojená. Všimněte si, že pokud budete postupovat thecord kolem uzlu, přechody „over – under“ se budou střídat.Poté pokračoval v experimentování se dvěma smyčkami a způsoby, jakými by mohly být svázány dohromady. Zde jsou zobrazeny uzly s až šestipřekroky pro jednu smyčku.
Jedním z výsledků Tait studie byla jeho Hamiltonian graf dohad.
mapa je považována za mnohostěn nakreslený na kouli a může být promítnut do roviny. Tait navrhl, aby každá kubická polyhedrální mapa měla Hamiltoniánský cyklus . Taitova metoda se zaměřila na okraje grafu aukázal, že Hamiltonovský cyklus může vytvořit čtyřbarevnou mapu. Teprve v roce 1946 našel William Tutte (1917-2002) první protipříklad Taitovy domněnky.
Tait a spojení s uzly
Taitinitiated studium naštvaným v roce 1880, když ukázal, že fourcolour věta je ekvivalentní tvrzení, že ne snark isplanar. Rovinný graf je ten, který lze nakreslit v roviněžádné překročení okrajů. Vypadá to, jako by Taitova myšlenka na neplanární grafymůže pocházet z jeho studia uzlů a Hamiltonovských drah .
první známý snark byl Petersen graf objevena v roce 1898,a matematici začali shánět více z těchto druhů graphsbut to nebylo až do roku 1946, že další snark byl nalezen.
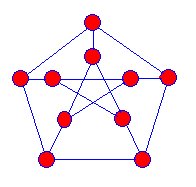 |
Naštvaným jsou projekce trojrozměrné grafy na theplane. Neexistují žádné vrcholy, kde se objevují modré okrajenávzájem. Snarky mají následující vlastnosti:
|
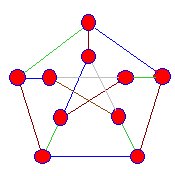 |
hrany setkání vrcholy tohoto snark jsou barevné modré,zelené a hnědé, ale my jsme vždy dosáhnout fáze, kde to processcannot být i nadále. |
Julia Peterson (1839-1910)
Lov theSnark je báseň, kterou napsal Lewis Carroll, a Martin Gardnernamed tyto grafy Naštvaným, protože byli tak nepolapitelný.
transformace problému a hledání nových metod.
i když Heawood našel hlavní chybu v Kempe je důkaz, metoda in1890, byl schopen jít na to, aby dokázal, čtyři barvy věta, ale učinil významný průlom a přesvědčivě dokázal všechny mapy by mohly být colouredwith pěti barvách.
Heawood významně přispěl k problému a přesunul pozornost z oblastí mapy na hranice mezi nimi. Do roku 1898 dokázal, že je-li počet krajů v jednotlivých krajích dělitelný 3, mohly by být regiony obarveny čtyřmi barvami.
Cauchyova důkaz Eulerova vzorce také nápad thatany síť mnohostěnu může být trojúhelníkový přidáním hrany makenon-trojúhelníkové plochy na trojúhelníky. Poté vypracoval postup, kdy okraje jeden po druhém vymazal, což ukazuje, že Eulerova forma může být zachována na každém kroku.
Cauchyova Důkaz Eulerova Vzorce
Cauchyova 1813 důkaz Eulerovy Formule začal s myšlenkou aprojection mnohostěnu získat letadlo čisté. Dále prokázal (a), že jakákoli síť může být triangulována, a jeho důkaz(b) Eulerova vzorce byl v té době přijat.
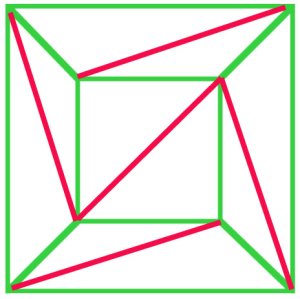 (a)
|
In principle, every polygonal net can be triangulated. In thisnet of a cube (a), $f + v – e$ is $10 + 8 – 17 = 1$, and Euler’sformula still holds. |
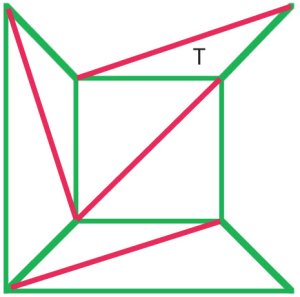 (b)
|
Cauchyova argumentem bylo odstranit vnější hrany z grafu(a), jeden po druhém, a když už se dostali do fáze, stejně jako v diagramu (b)odstraněn celý trojúhelník T, tedy zachování Eulerova vzorce. Mnozí z počátku devatenáctého století se shodli na tompostup prokázal důkaz Eulerova vzorce pro allpolyhedra. |
v roce 1900, matematici věděli, že rovinný graf lze beconstructed z jakékoliv mapě pomocí silný koncept duality . V duálu jsou teregiony reprezentovány vrcholy a dva vrcholy jsou spojeny hranou, pokud regiony sousedí. V těchto grafech se Fourcolour domněnka nyní ptá, zda vrcholy grafu mohou být zbarveny 4 barvami, takže žádné dva sousední vrcholy nejsou stejnou barvou.
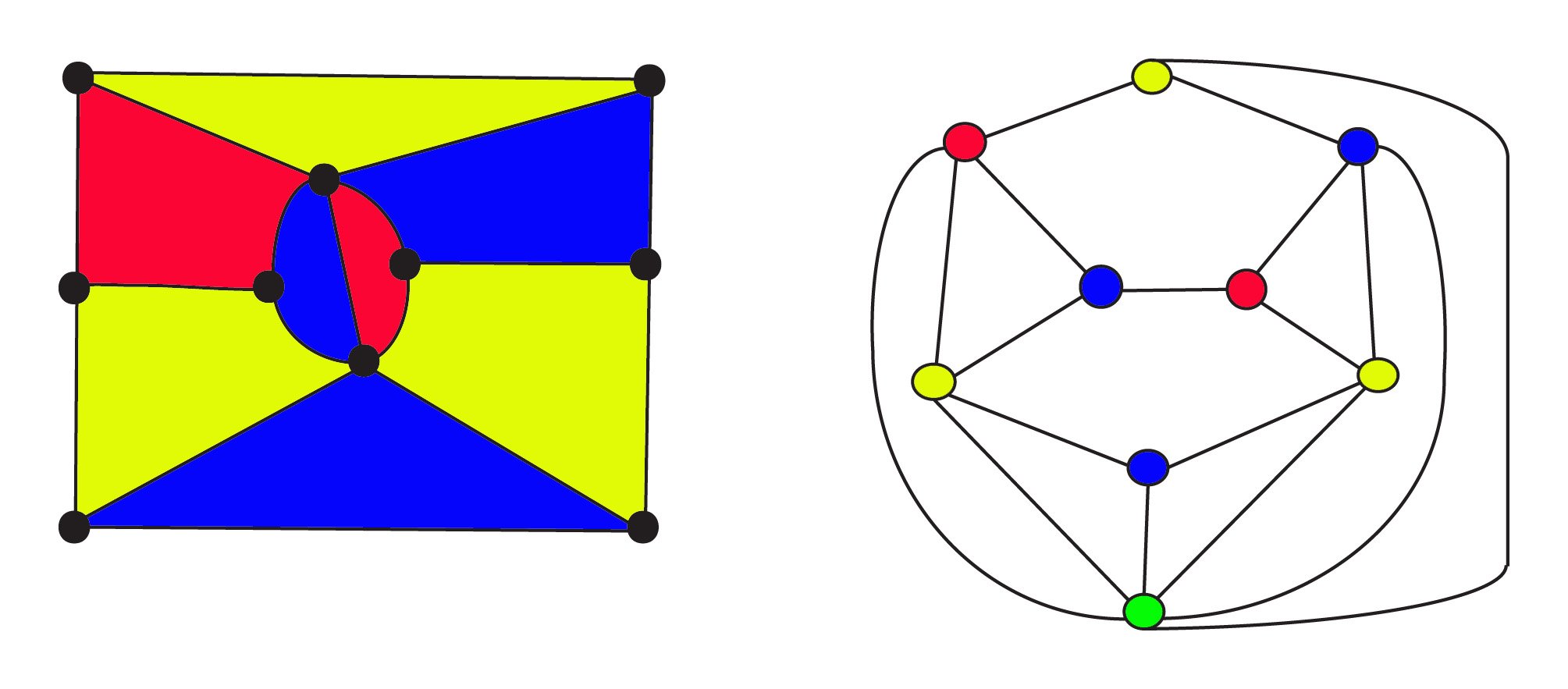
3-barevná mapa na levé straně je$8$ regionů $10$ vrcholů a $17$ hran. Jeho duální graf na theright má$ 9 $ regiony$ 9 $ vrcholy a $ 17 $ hrany, kde thevertices jsou barevné stejně jako oblasti mapy. Greenvertex ve spodní části grafu představuje nekonečnou vnější oblast mapy. Jak původní mapa, tak její duální Eulerova formula pro sítě $f + v-e = 1$ nebo, $\text{regiony} +\text{vrcholy} – \text{hrany} = 1$. Vztah duality je asymetrický: dvojkou duálu bude původní graf, kde se vyměňují giony a vrcholy.
Během první poloviny dvacátého století, mathematiciansfocused o úpravě těchto druhů techniky reducecomplicated mapy speciální případy, které by mohly být identifikovány andclassified, zkoumat jejich konkrétní vlastnosti anddeveloped myšlenka minimální sadu map konfigurace thatcould být testovány.
V první řadě, bylo, že obsahují nearly9,000 členů, což byl obrovský úkol, a tak mathematiciansturned počítačové techniky psát algoritmy, které by mohl udělat thetesting pro ně. Algoritmy používané modifikované verze Kempe’soriginal nápad řetězů spolu s dalšími techniky reducethe počet členů minimální sadu.
Po spolupráci s John Koch na problém ofreducibility, v roce 1976 na Univerzitě v Illinois, Kenneth Appeland Wolfgang Haken nakonec snížena na testování problém anunavoidable set s 1,936 konfigurace, a kompletní solutionto Čtyři Barvy Domněnkou bylo dosaženo. Tento problém kontroly redukovatelnosti map jeden po druhém byl dvakrát zkontrolováns různými programy a různými počítači. Jejich důkaz ukázal, že alespoň jedna mapa s nejmenším možným počtem oblastí vyžadujících pět barev nemůže existovat.
od prvního důkazu byly nalezeny efektivnější algoritmy pro 4-barevné mapy a do roku 1994 byla nevyhnutelná sada konfigurací snížena na 633.
je „důkaz“ provedený na počítači řádným důkazem?
protože důkaz byl proveden pomocí počítače, došlo k okamžitému výkřiku. Mnoho matematiků a filozofů tvrdilo, že důkaz nebyl legitimní. Někteří říkali, že důkazy shouldonly být ‚dokázala‘ lidé, ne stroje, zatímco jiní, z vícepraktické mysli zpochybnil spolehlivost obou algorithmsand schopnost stroje vykonávat bez chyby.Nicméně, mnoho důkazů napsaných matematiky bylozjistil, že je vadný, takže argument o spolehlivosti se zdá být prázdný.Ať už názory, situace se vyrábí seriousdiscussion o povaze důkazu, který stále continuestoday.
pro pedagogické poznámky:
použijte kartu Poznámky v horní části tohoto článku nebo klikněte zde .
poznámky
- více podrobností o tomto a dalších postupech nalezených v této části lze vidět v knize Robina Wilsona Čtyři barvy postačí .
- uzly mohou být leváky nebo praváky a dnes existujídůležité aplikace této vlastnosti v chemii,farmacii, biologii a fyzice. (Viz pedagogické poznámky)
- pojmenované po William Rowan Hamilton (1805-1865). Hamiltonovská cesta v grafu navštívíkaždý vrchol přesně jednou. Hamiltonovský cyklus (nebo obvod) je apath, který navštíví každý vrchol přesně jednou a vrátí se do výchozího vrcholu.(Viz pedagogické poznámky)
- kniha Imre Lakatos, důkazy a vyvrácení má adiskuse a kritiku Cauchyho postupu (strany 6-12) a mnohem více o příběhu Eulerovy věty.
- myšlenka duality vznikla v 16. a 17. stoletívývoj v projektivní geometrii. Matematici jako Pascal andDesargues zjistili, že nové věty lze nalézt výměnou tetermů „point“ a „line“ v popisech určitých geometrických konfigurací. Příkladem je pravidelná polyhedra, kdeverticles jednoho odpovídají obličejům druhého. Takže dvojka čtyřstěnu je další čtyřstěn a dvojka krychle je osmistěn. Duální duální je originálpolyhedron.
velmi populární, snadno čitelná kniha o čtyřech ColourTheorem je:
Wilson, R. (2003)
postačí Čtyři barvy.
Londýn. Tučňák Knihy.
Pro podrobnější a technické historie, standardreference kniha je:
Biggs, N.; Lloyd, E. & Wilson, R. (1986) (1998)
Teorie Grafů,1736-1936
Oxford. Oxford University Press.
Tento nás přivádí k dnešnímu dni, s novějšími základy afilosofie.
Fritsch, R a Fritsch, G (2000)
čtyřbarevná věta: historie, topologické základy a myšlenka důkazu
New York. Springer-Verlag.
Téměř žádné obecné dějiny kniha má mnohem na toto téma, ale poslední kapitola v Katz nazývá Počítačů a Aplikací má asection na Teorii Grafů, a Čtyři Barvy Věta je mentionedtwice.
Polya G. jak SolveIt.
Toto je klasická kniha o řešení problémů. There have beenmany vydání této knihy, protože se poprvé objevil v roce 1950 aje stále snadno dostupné. Je zajímavé, že nedávné vydání bylydát podtitul „nový aspekt matematické metody“.
Lakatos, i. (1976) důkazy arefutace: logika matematického objevu.
Cambridge. C. U. P.
To je další důležitá kniha, která vedla k výzkumu intoProblem Řešení a Vyšetřování v roce 1970. Začíná to jako aclassroom diskuse mezi učitelem a skupinou studentsabout důkaz Eulerova vzorce, a pohybuje se přes nápady,námitky a možností, které byly diskutovány bymathematicians a vědci v devatenáctém století. To raisessome z nejdůležitějších otázek o výuce a learningproblém řešení a o matematických metod a důkazu.
Související odkazy
už nějakou dobu jsem měl malou knihu o Stringových hrách. Když jsem byl ve škole, říkalo se tomu kočičí kolébka a hráli jsme to v naší době.
nedávno francouzský časopis publikoval článek o „algebře“ strunných postav! Pokud jste jít na Amazon najdete anice kniha Ann Swain a Michael Taylor nazývá Prst Struny: Kniha Kočky, Kolébky andString Údaje zveřejní Floris books v September2008. Tam jsou některé 80 Obrázky popsané s barevnými diagrams.It spirála je vázána, takže zůstane otevřená, zatímco budete postupovat podle pokynů. Dodává se také s několika smyčkami!
pro odborníky na uzly je AshleyBook uzlů klasikou pro každého, kdo má zájemstovky různých druhů uzlů a jejich použití. Amazon márůzné edice dostupné za různé ceny.
Odkazy
Pro obecný přehled a odkazy na mnoho lidí a témat, theMacTutor webové stránky je
A samozřejmě MacTutor životopisy těch, kteří jsou zapojeni v rozvojových všechny různé matematické aspekty lze nalézt na MacTutor Životopisy Index.
čtyři barevné věty a tři důkazy. Pro matematickypersistent následující webové stránky má zajímavý nový přístup k útoku na problém konstrukce nového algoritmu pro řešení problému, a vázání snížit závislost na počítači.http://www.emu.edu.tr/~cahit/the%20four%20color%20theorem%20—%20three%20proofs.htm
pro teorii grafů poskytuje Wikipedia dobrý přehled a můžete získat opravdu technické věci. Ukazuje druhy moderníchaplikace této oblasti matematiky. Pokud přejdete na GraphColouring a kliknete na větu Four Color, pak najdetemnohem více informací.
zajímavá a ne příliš technická historie teorie uzlů – jak se myšlenka z Kelvinovy fyziky vrací k atomové Teoriidnes.
Asociace učitelů matematiky má Celtic Knotdesign plakáty. Přejděte na jejich webové stránky a procházejte abeceduseznam zdrojů.
zjistěte vše o uzlech na atlasu uzlů! Pokud nejste anexpert-stačí si užít pestrost a komplexnost databáze „v duchu wiki“
více umělecké a barevné – ale neméně matematické je místo spiknutí.
pro ty, kteří chtějí některé z původních věcí a historicaldetail jít do historie teorie uzlů na: