regresia către medie este un fenomen statistic comun care ne poate induce în eroare atunci când observăm lumea. Învățarea de a recunoaște când regresia la medie este în joc ne poate ajuta să evităm interpretarea greșită a datelor și să vedem modele care nu există.

***

este important să minimalizăm cazurile de judecată proastă și să abordăm punctele slabe din raționamentul nostru. Învățarea despre regresie la medie ne poate ajuta.psihologul Daniel Kahneman, laureat al Premiului Nobel, a scris o carte despre prejudecăți care ne întunecă raționamentul și ne distorsionează percepția asupra realității. Se pare că există un întreg set de erori logice pe care le comitem, deoarece intuiția și creierul nostru nu se ocupă bine de statistici simple. Una dintre erorile pe care le examinează în gândirea rapidă și lentă este regresia infamă către medie.

noțiunea de regresie la medie a fost elaborată pentru prima dată de Sir Francis Galton. Regula spune că, în orice serie cu fenomene complexe care depind de multe variabile, unde este implicată șansa, rezultatele extreme tind să fie urmate de cele mai moderate.

în căutarea înțelepciunii, Peter Bevelin oferă exemplul lui John, care era nemulțumit de performanța noilor angajați, așa că i-a pus într-un program de îmbunătățire a abilităților, unde a măsurat abilitățile angajaților:

scorurile lor sunt acum mai mari decât erau la primul test. Concluzia lui John: „programul de îmbunătățire a abilităților a determinat îmbunătățirea abilităților.”Acest lucru nu este neapărat adevărat. Scorurile lor mai mari ar putea fi rezultatul regresiei la medie. Deoarece acești indivizi au fost măsurați ca fiind la capătul scăzut al scalei de calificare, ei ar fi arătat o îmbunătățire chiar dacă nu ar fi luat programul de îmbunătățire a abilităților. Și ar putea exista multe motive pentru performanța lor anterioară — stres, oboseală, boală, distragere a atenției etc. Poate că adevărata lor abilitate nu s-a schimbat.

performanța noastră variază întotdeauna în jurul unei performanțe medii reale. Performanța extremă tinde să devină mai puțin extremă data viitoare. De ce? Măsurătorile de testare nu pot fi niciodată exacte. Toate măsurătorile sunt alcătuite dintr-o parte adevărată și o parte de eroare aleatorie. Când măsurătorile sunt extreme, este posibil ca acestea să fie parțial cauzate de întâmplare. Șansa este probabil să contribuie mai puțin la a doua oară când măsurăm performanța.dacă trecem de la un mod de a face ceva la altul doar pentru că nu reușim, este foarte probabil să ne descurcăm mai bine data viitoare, chiar dacă noul mod de a face ceva este egal sau mai rău.

acesta este unul dintre motivele pentru care este periculos să extrapolați de la dimensiuni mici ale eșantioanelor, deoarece datele ar putea să nu fie reprezentative pentru distribuție. De asemenea, James March susține că, cu cât cineva rămâne mai mult la locul de muncă, „cu atât este mai mică diferența probabilă dintre înregistrarea observată a performanței și capacitatea reală.”Orice se poate întâmpla pe termen scurt, mai ales în orice efort care implică o combinație de îndemânare și noroc. (Raportul dintre abilitate și noroc influențează, de asemenea, regresia la medie.)

regresia la medie

efectele regresiei la medie pot fi observate frecvent în sport, unde efectul provoacă o mulțime de speculații nejustificate.

în Thinking Fast and Slow, Kahneman își amintește că a urmărit saltul de schi masculin, o disciplină în care scorul final este o combinație de două salturi separate. Conștient de regresia la medie, Kahneman a fost surprins să audă predicțiile comentatorului despre al doilea salt. El scrie:

Norvegia a avut un prim salt grozav; va fi tensionat, sperând să-și protejeze avantajul și probabil va face mai rău” sau „Suedia a avut un prim salt rău și acum știe că nu are nimic de pierdut și va fi relaxat, ceea ce ar trebui să-l ajute să facă mai bine.

Kahneman subliniază că comentatorul a observat regresia la medie și a venit cu o poveste pentru care nu existau dovezi cauzale (vezi eroarea narativă). Asta nu înseamnă că povestea lui nu poate fi adevărată. Poate, dacă am măsura ritmul cardiac înainte de fiecare salt, am vedea că sunt mai relaxați dacă primul salt ar fi rău. Cu toate acestea, nu asta este ideea. Ideea este că regresia la medie se întâmplă atunci când norocul joacă un rol, așa cum a făcut-o în rezultatul primului salt.

lecția din sport se aplică oricărei activități în care șansa joacă un rol. Adesea atașăm explicații ale influenței noastre asupra unui anumit proces la progresul sau lipsa acestuia.

în realitate, știința performanței este complexă, dependentă de situație și adesea o mare parte din ceea ce credem că este sub controlul nostru este cu adevărat aleator.

în cazul săriturilor de schi, un vânt puternic împotriva jumperului va duce chiar și la cel mai bun atlet care prezintă rezultate mediocre. În mod similar, un vânt puternic și condiții de schi în favoarea unui jumper mediocru poate duce la o creștere considerabilă, dar temporară a rezultatelor sale. Cu toate acestea, aceste efecte vor dispărea odată ce condițiile se schimbă și rezultatele vor regresa înapoi la normal.

acest lucru poate avea implicații serioase pentru coaching și urmărirea performanței. Regulile de regresie sugerează că atunci când evaluăm performanța sau angajarea, trebuie să ne bazăm mai mult pe înregistrări decât pe rezultatele unor situații specifice. În caz contrar, suntem predispuși să fim dezamăgiți.

când Kahneman a ținut o prelegere Forțelor Aeriene israeliene despre psihologia instruirii eficiente, unul dintre ofițeri și-a împărtășit experiența că extinderea laudelor către subordonații săi a dus la performanțe mai slabe, în timp ce certarea a dus la o îmbunătățire a eforturilor ulterioare. În consecință, el devenise generos cu feedback negativ și devenise destul de precaut să dea prea multe laude.

Kahneman a observat imediat că a fost regresie la media la locul de muncă. El a ilustrat concepția greșită printr-un exercițiu simplu pe care poate doriți să-l încercați singur. El a desenat un cerc pe o tablă și apoi le-a cerut ofițerilor unul câte unul să arunce o bucată de cretă în centrul cercului cu spatele orientat spre tablă. Apoi a repetat experimentul și a înregistrat performanța fiecărui ofițer în primul și al doilea proces.desigur, cei care s-au descurcat incredibil de bine la prima încercare au avut tendința de a face mai rău la a doua încercare și invers. Eroarea a devenit imediat clară: schimbarea performanței are loc în mod natural. Asta din nou nu înseamnă că feedback – ul nu contează deloc-poate că nu, dar ofițerul nu a avut nici o dovadă pentru a concluziona că a făcut-o.

corelația imperfectă și șansa

În acest moment, s-ar putea să vă întrebați de ce se întâmplă regresia la medie și cum ne putem asigura că suntem conștienți de ea atunci când apare.

pentru a înțelege regresia la medie, trebuie să înțelegem mai întâi corelația.

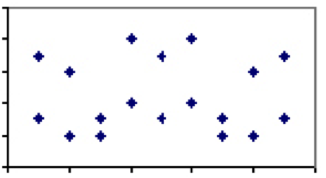
coeficientul de corelație dintre două măsuri care variază între -1 și 1, este o măsură a ponderii relative a factorilor pe care îi împărtășesc. De exemplu, două fenomene cu puțini factori împărțiți, cum ar fi consumul de apă îmbuteliată versus rata sinuciderii, ar trebui să aibă un coeficient de corelație apropiat de 0. Adică, dacă ne-am uita la toate țările din lume și am trasa ratele sinuciderilor dintr-un anumit an față de consumul de apă îmbuteliată pe cap de locuitor, complotul nu ar arăta deloc un model.

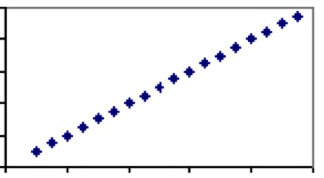
dimpotrivă, există măsuri care depind exclusiv de același factor. Un bun exemplu în acest sens este temperatura. Singurul factor care determină temperatura-viteza moleculelor-este împărțit de toate scalele, prin urmare fiecare grad în Celsius va avea exact o valoare corespunzătoare în Fahrenheit. Prin urmare, temperatura în grade Celsius și Fahrenheit va avea un coeficient de corelație de 1, iar parcela va fi o linie dreaptă.

există puține fenomene în științele umane care au un coeficient de corelație de 1. Există, totuși, o mulțime în care asocierea este slabă până la moderată și există o anumită putere explicativă între cele două fenomene. Luați în considerare corelația dintre înălțime și greutate, care ar ateriza undeva între 0 și 1. În timp ce practic fiecare copil de trei ani va fi mai ușor și mai scurt decât fiecare bărbat adult, nu toți bărbații maturi sau copiii de trei ani de aceeași înălțime vor cântări la fel.

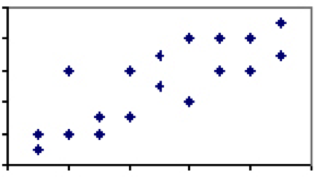
această variație și gradul inferior corespunzător de corelație implică faptul că, în timp ce înălțimea este în general un predictor bun, există în mod clar alți factori decât înălțimea în joc. Când corelația a două măsuri este mai puțin decât perfectă, trebuie să fim atenți la efectele regresiei la medie.

Kahneman a observat o regulă generală: ori de câte ori corelația dintre două scoruri este imperfectă, va exista regresie la medie.

Acest lucru la început ar putea părea confuz și nu foarte intuitiv, dar gradul de regresie la medie este direct legat de gradul de corelare a variabilelor. Acest efect poate fi ilustrat cu un exemplu simplu.

presupuneți că sunteți la o petrecere și întrebați de ce femeile extrem de inteligente tind să se căsătorească cu bărbați care sunt mai puțin inteligenți decât sunt. Majoritatea oamenilor, chiar și cei cu o anumită pregătire în statistici, vor sări rapid cu o varietate de explicații cauzale, de la evitarea concurenței până la temerile de singurătate cu care se confruntă aceste femei. Un subiect de astfel de controverse este probabil să stârnească o mare dezbatere.acum, dacă am întreba De ce corelația dintre scorurile de inteligență ale soților este mai puțin decât perfectă? Această întrebare nu este la fel de interesantă și este puțin de ghicit – știm cu toții că acest lucru este adevărat. Paradoxul constă în faptul că cele două întrebări se întâmplă să fie echivalente algebric. Kahneman explică:

dacă corelația dintre inteligența soților este mai mică decât perfectă (și dacă bărbații și femeile în medie nu diferă în inteligență), atunci este o inevitabilitate matematică că femeile extrem de inteligente vor fi căsătorite cu soți care sunt în medie mai puțin inteligenți decât sunt (și invers, desigur). Regresia observată la medie nu poate fi mai interesantă sau mai explicabilă decât corelația imperfectă.

presupunând că corelația este imperfectă, șansele ca doi parteneri să reprezinte primii 1% în ceea ce privește orice caracteristică este mult mai mică decât un partener care reprezintă primii 1%, iar celălalt – cei 99% inferiori.

cauza, efectul și tratamentul

ar trebui să fim deosebit de atenți la regresia la fenomenul mediu atunci când încercăm să stabilim cauzalitatea între doi factori. Ori de câte ori corelația este imperfectă, cel mai bun va părea întotdeauna să se înrăutățească și cel mai rău va părea să se îmbunătățească în timp, indiferent de orice tratament suplimentar. Acesta este un lucru pe care mass-media generală și, uneori, chiar și oamenii de știință instruiți nu reușesc să-l recunoască.

luați în considerare exemplul dat de Kahneman:

copiii deprimați tratați cu o băutură energizantă se îmbunătățesc semnificativ pe o perioadă de trei luni. Am făcut acest titlu de ziar, dar faptul că rapoartele este adevărat: dacă ați tratat un grup de copii deprimați de ceva timp cu o băutură energizantă, acestea ar arăta o îmbunătățire semnificativă clinic. Este, de asemenea, cazul în care copiii deprimați care petrec ceva timp în picioare pe cap sau îmbrățișează o pisică timp de douăzeci de minute pe zi vor arăta, de asemenea, îmbunătățiri.

ori de câte ori vine peste astfel de titluri este foarte tentant pentru a sări la concluzia că băuturile energizante, în picioare pe cap sau îmbrățișarea pisici sunt toate cure perfect viabile pentru depresie. Cu toate acestea, aceste cazuri întruchipează încă o dată regresia la medie:

copiii deprimați sunt un grup extrem, sunt mai deprimați decât majoritatea celorlalți copii—iar grupurile extreme regresează la medie în timp. Corelația dintre scorurile depresiei în ocazii succesive de testare este mai puțin decât perfectă, astfel încât va exista o regresie la medie: copiii deprimați se vor îmbunătăți oarecum în timp, chiar dacă nu îmbrățișează pisici și nu beau Red Bull.

adesea atribuim greșit o politică sau un tratament specific ca fiind cauza unui efect, când schimbarea grupurilor extreme s-ar fi întâmplat oricum. Aceasta prezintă o problemă fundamentală: cum putem ști dacă efectele sunt reale sau pur și simplu datorate variabilității?

Din fericire, există o modalitate de a spune între o îmbunătățire reală și regresie la medie. Aceasta este introducerea așa-numitului grup de control, care se așteaptă să se îmbunătățească doar prin regresie. Scopul cercetării este de a determina dacă grupul tratat se îmbunătățește mai mult decât poate explica regresia.

în situațiile din viața reală cu performanța anumitor indivizi sau Echipe, unde singurul punct de referință real este performanța trecută și nu poate fi introdus niciun grup de control, efectele regresiei pot fi dificile, dacă nu chiar imposibil de dezlegat. Putem compara cu media industriei, colegii din grupul de cohortă sau ratele istorice de îmbunătățire, dar niciuna dintre acestea nu este o măsură perfectă.

***

Din fericire, conștientizarea regresiei la fenomenul mediu în sine este deja un prim pas important către o abordare mai atentă a înțelegerii Norocului și a performanței.

dacă există ceva de învățat de la regresie la medie, este importanța înregistrărilor, mai degrabă decât să se bazeze pe povești de succes unice. Sper că data viitoare când veți întâlni o calitate extremă în parte guvernată de șansă, veți realiza că efectele sunt susceptibile de a regresa în timp și vă vor ajusta așteptările în consecință.

ce să citiți în continuare

• Îmbunătățiți-vă gândirea cu 113 modele mentale explicate.
• citiți despre gândirea de nivelul doi, astfel încât să puteți evita consecințele negative.