Nota editorului

următorul raport de cercetare a studenților a fost pregătit pentru clasa de matematică 255 a profesorului Judit Kardos, care a avut loc la Colegiul din New Jersey. Acesta a fost un curs introductiv de 3 credite în istoria matematicii. Acest raport a fost calculat la 30% din nota finală. Este un exemplu al tipului de cercetare istorică pe care studenții o pot face folosind surse secundare.

soluția lui Leonard Euler la problema podului K. N. Nigsberg

K. N. Nigsberg

povestea noastră începe în secolul al 18-lea, în ciudatul oraș K. Nigsberg, Prusia, pe malurile râului Pregel. În 1254, cavalerii teutoni au fondat orașul K-Nigsberg sub conducerea regelui boem Ottoker al II-lea după a doua lor cruciadă împotriva prusacilor. În Evul Mediu, K a devenit un oraș și un centru comercial foarte important, cu locația sa poziționată strategic pe râu. Opera de arta din secolul al XVIII-lea prezinta K Centicturnigsberg ca un oraș înfloritor, în cazul în care flotele de nave umple Pregel, și comerțul lor oferă un stil de viață confortabil atât comercianților locali și familiile lor. Economia sănătoasă a permis oamenilor din oraș să construiască șapte poduri peste râu, dintre care majoritatea conectate la insula Kneiphof; locațiile lor pot fi văzute în imaginea însoțitoare .

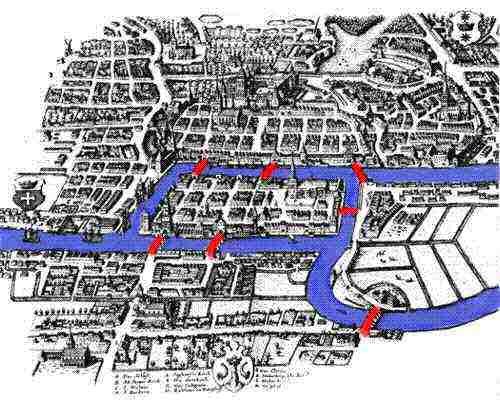
pe măsură ce râul curgea în jurul Kneiphof, adică literalmente pub yard și o altă insulă, a împărțit orașul în patru regiuni distincte. Cele șapte poduri au fost numite Podul Fierarului, Podul de legătură, Podul Verde, Podul comerciantului, Podul de lemn, Podul Înalt și Podul mierii. Potrivit lore, cetățenii din K-Nigsberg obișnuiau să petreacă după-amiaza de duminică plimbându-se în jurul frumosului lor oraș. În timp ce se plimbau, oamenii orașului au decis să creeze un joc pentru ei înșiși, scopul lor fiind acela de a concepe un mod în care să poată merge în jurul orașului, traversând fiecare dintre cele șapte poduri o singură dată. Chiar dacă niciunul dintre cetățenii din K-Nigsberg nu a putut inventa un traseu care să le permită să traverseze fiecare dintre poduri o singură dată, totuși nu au putut dovedi că este imposibil. Din fericire pentru ei, K Inktoknigsberg nu era prea departe de Sankt Petersburg, casa celebrului matematician Leonard Euler.

Euler și problema podului

de ce s-ar preocupa Euler de o problemă atât de lipsită de legătură cu domeniul matematicii? De ce un matematician atât de mare ar petrece mult timp cu o problemă banală precum problema podului K-Nigsberg? Euler a fost evident un om ocupat, publicând peste 500 de cărți și lucrări în timpul vieții sale. Numai în 1775, a scris în medie o lucrare matematică pe săptămână, iar în timpul vieții sale a scris pe o varietate de subiecte în afară de matematică, inclusiv mecanică, optică, astronomie, navigație și hidrodinamică. Nu este surprinzător faptul că Euler a considerat că această problemă este banală, afirmând într-o scrisoare din 1736 către Carl Leonhard Gottlieb Ehler, Primarul din Danzig, care i-a cerut o soluție la problemă :

. . . Astfel, vedeți, domnule nobil, cum acest tip de soluție are o relație mică cu matematica și nu înțeleg de ce vă așteptați ca un matematician să o producă, mai degrabă decât oricine altcineva, pentru că soluția se bazează doar pe rațiune, iar descoperirea ei nu depinde de niciun principiu matematic. Din această cauză, nu știu de ce chiar și întrebările care au o relație atât de mică cu matematica sunt rezolvate mai repede de matematicieni decât de alții.

chiar dacă Euler a găsit problema banală, el a fost încă intrigat de ea. Într-o scrisoare scrisă în același an lui Giovanni Marinoni, un matematician și inginer Italian, Euler a spus:

această întrebare este atât de banală, dar mi s-a părut demnă de atenție în faptul că geometria, nici algebra, nici măcar arta numărării nu au fost suficiente pentru a o rezolva.

Euler credea că această problemă era legată de un subiect pe care Gottfried Wilhelm Leibniz îl discutase cândva și dorea să lucreze cu el, lucru pe care Leibniz îl numea geometria situs sau geometria poziției. Această așa-numită geometrie a poziției este ceea ce se numește acum teoria grafurilor, pe care Euler o introduce și o folosește în timp ce rezolvă această faimoasă problemă.

dovada lui Euler

la 26 August 1735, Euler prezintă o lucrare care conține soluția la problema podului Konigsberg. El abordează atât această problemă specifică, cât și o soluție generală cu orice număr de mase terestre și orice număr de poduri. Această lucrare, numită Solutio problematis ad geometriam situs pertinentis, a fost publicată mai târziu în 1741 . Lucrarea lui Euler este împărțită în douăzeci și unu de paragrafe numerotate și, în cele ce urmează, va fi prezentată o versiune simplificată a paragrafelor lui Euler.

în primele două paragrafe ale dovezii lui Euler, el introduce problema podului Konigsberg. În paragraful 1, Euler afirmă că el crede că această problemă se referă la geometrie, dar nu geometria bine cunoscută de contemporanii săi, care implică măsurători și calcule, ci în schimb un nou tip de geometrie, pe care Leibniz l-a denumit geometria poziției. Apoi, în paragraful 2, Euler explică publicului său cum funcționează problema Konigsberg. Euler a furnizat o schiță a problemei (vezi Figura 1 a lui Euler) și a numit cele șapte poduri distincte: A, b, c, d, e, f, și, g. în acest paragraf el afirmă întrebarea generală a problemei: „se poate afla dacă este sau nu posibil să traversăm fiecare pod exact o dată?”

Figura 1 a lui Euler din „Solutio problematis ad geometriam situs pertinentis,” Enestr 53

după enunțarea întrebării generale pe care încearcă să o rezolve, Euler începe să exploreze diferite metode de găsire a unei soluții. În paragraful 3, Euler îi spune cititorului că, pentru a rezolva această problemă specifică, ar putea scrie toate căile posibile, dar această tehnică ar dura mult timp și nu ar funcționa pentru configurații mai mari cu mai multe poduri și mase de teren. Din cauza acestor probleme, Euler a decis să aleagă o metodă diferită pentru rezolvarea acestei probleme.

în paragraful 4, el începe să simplifice problema inventând un sistem convenabil pentru a reprezenta trecerea unui pod. Euler decide că, în loc să folosească literele mici pentru a reprezenta traversarea unui pod, va scrie literele majuscule reprezentând masele terestre. De exemplu, referindu-se la figura 1, AB ar însemna o călătorie care a început în masa terestră a și s-a încheiat în B. Mai mult, dacă după călătoria de la masa terestră a la B, cineva decide să se mute în masa terestră D, aceasta ar fi pur și simplu notată, ABD. În paragraful 5, Euler își continuă discuția cu privire la acest proces explicând că în ABDC, deși există patru majuscule, au fost traversate doar trei poduri. Euler explică faptul că, indiferent de câte poduri există, va mai exista o scrisoare care să reprezinte trecerea necesară. Din această cauză, întreaga problemă a podului K. Nigsberg a necesitat traversarea a șapte poduri și, prin urmare, opt majuscule.în paragraful 6, Euler continuă să explice detaliile metodei sale. El îi spune cititorului că, dacă există mai multe poduri care pot fi traversate atunci când mergeți de la o masă terestră la alta, nu contează ce pod este folosit. De exemplu, chiar dacă există două poduri, a și b, care pot duce un călător de la A la B, nu contează cu notația lui Euler care pod este luat. În acest paragraf, Euler discută, de asemenea, problema specifică cu care se confruntă. El explică, folosind figura sa originală, că problema K-Nigsberg are nevoie exact de opt litere,unde perechile de (a,B) și (a, C) trebuie să apară una lângă alta exact de două ori, indiferent de litera care apare prima. În plus,perechile (A, D), (B, D) și (C,D) trebuie să apară împreună exact o dată pentru ca o cale care traversează fiecare pod o dată și o singură dată să existe.

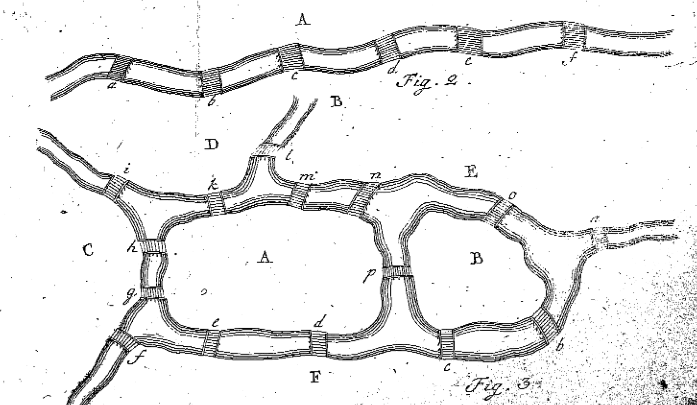
figurile 2 și 3 ale lui Euler din ‘Solutio problematis ad geometriam situs pertinentis,’ Enestr 53

în paragraful 7, Euler informează cititorul că fie trebuie să găsească o secvență de opt litere care să satisfacă problema, fie trebuie să demonstreze că nu există o astfel de secvență. Înainte de a face acest lucru pentru problema podului K, el decide să găsească o regulă pentru a descoperi dacă există o cale pentru o problemă mai generală. El face acest lucru la punctul 8 uitându-se la un exemplu mult mai simplu de mase terestre și poduri. Euler desenează Figura 2 și începe să evalueze situațiile în care regiunea A este parcursă. Euler afirmă că, dacă podul a este parcurs o dată, A a fost fie locul în care călătoria a început, fie s-a încheiat și, prin urmare, a fost folosit o singură dată. Dacă punțile A, b și c sunt toate parcurse o dată, A este folosit exact de două ori, indiferent dacă este locul de început sau de sfârșit. În mod similar, dacă cinci poduri duc la A, masa terestră A ar apărea exact de trei ori în călătorie. Euler afirmă că, „în general, dacă numărul de poduri este orice număr impar și dacă este mărit cu unul, atunci numărul de apariții ale lui A este jumătate din rezultat.”Cu alte cuvinte, dacă există un număr impar de poduri care leagă A de alte mase terestre, adăugați unul la numărul de poduri și împărțiți-l la două, pentru a afla de câte ori trebuie utilizat A în cale, unde fiecare pod este folosit o singură dată (adică. Aparițiile totale ale lui A unde A are un impar # de poduri = (#de Poduri – 1) / 2 ).

folosind acest fapt, Euler rezolvă problema podului K de la punctul 9. În acest caz, deoarece există cinci poduri care duc la A, trebuie să apară de trei ori (vezi figura lui 1, de mai sus). În mod similar, B, C și D trebuie să apară de două ori, deoarece toate au trei poduri care duc la ele. Prin urmare, 3(pentru A) + 2(Pentru B) + 2(Pentru C) + 2(pentru D) = 9, dar Euler a afirmat deja că trebuie să existe doar opt apariții pentru cele șapte poduri. Aceasta este o contradicție! Prin urmare, este imposibil să călătorești podurile din orașul K Centictnigsberg o singură dată și o singură dată. Sfârșitul, sau este? În timp ce oamenii din K. Nigsberg ar putea fi mulțumiți de această soluție, marele matematician Leonhard Euler nu a fost mulțumit. Euler își continuă dovada pentru a face față unor situații mai generale.

generalizarea lui Euler

în paragraful 10, Euler își continuă discuția observând că, dacă situația implică toate masele terestre cu un număr impar de poduri, este posibil să se spună dacă o călătorie poate fi făcută folosind fiecare pod o singură dată. Euler afirmă că, dacă suma de câte ori trebuie să apară fiecare literă este încă una decât numărul total de poduri, se poate face o călătorie. Cu toate acestea, dacă numărul de apariții este mai mare decât unul mai mult decât numărul de poduri, nu se poate face o călătorie, cum ar fi problema podului K. Acest lucru se datorează faptului că regula, pe care Euler o dă pentru un număr impar de poduri, folosind figura sa 2, este valabilă pentru situația generală dacă există doar o altă masă terestră sau mai multe.la punctele 11 și 12, Euler tratează situația în care o regiune are atașat un număr par de poduri. Această situație nu apare în problema K-Nigsberg și, prin urmare, a fost ignorată până acum. În situația cu o masă de teren X cu un număr par de poduri, pot apărea două cazuri. Primul caz este când X este punctul de plecare pentru călătorie. În acest caz, X va apărea de două ori, o dată ca punct de plecare și din nou ca punct final. În celălalt caz, X nu este punctul de plecare. Dacă acest lucru s-ar întâmpla, X ar apărea o singură dată, deoarece călătoria ar trebui să intre printr-un pod și să plece imediat prin Singurul altul disponibil. În mod similar, dacă există patru poduri atașate la X, numărul de apariții ale lui X depinde dacă este sau nu un punct de plecare. Dacă călătoria începe în X, trebuie să apară de trei ori, dar dacă nu începe în X, ar apărea doar de două ori. Deci, în general, dacă X are un număr par de poduri atașate, atunci dacă călătoria nu începe în X, X apare de jumătate din numărul de ori ca poduri (adică. Aparițiile lui X unde X este egal și nu punctul de plecare = (# de Poduri) / 2). Dacă călătoria începe în X, atunci X apare de jumătate din numărul de ori ca poduri, plus unul (adică apariții ale lui X unde X este par și punct de plecare = ((#de Poduri) / 2) + 1).

în paragrafele 13-15, Euler explică cum să ne dăm seama dacă există o cale care folosește fiecare pod o singură dată și prezintă propriul său exemplu pentru a arăta cum funcționează. Euler explică mai întâi metoda sa simplă în șase pași pentru a rezolva orice situație generală cu mase terestre împărțite de râuri și conectate prin poduri. Primul Euler denotă fiecare masă de teren cu o scrisoare de capital. În al doilea rând, el ia numărul total de poduri, adaugă unul și scrie acest lucru deasupra graficului pe care urmează să îl facă. Apoi, ia literele majuscule, le pune într-o coloană, iar lângă ele scrie numărul de poduri. În al patrulea rând, el indică cu asteriscuri masele terestre care au un număr par de poduri. Apoi, alături de fiecare număr par, scrie numărul de numărul unu, iar lângă fiecare număr impar plasează numărul de numărul unu plus numărul unu. În cele din urmă, Euler adaugă numerele scrise în coloana din dreapta și dacă suma este una mai mică sau egală cu numărul de poduri plus una, atunci călătoria necesară este posibilă. Cu toate acestea, este important să rețineți că, dacă suma este una mai mică decât numărul de poduri plus unul, atunci călătoria trebuie să înceapă de la una dintre masele de teren marcate cu un asterisc. Dacă suma este egală cu numărul de poduri plus unul, călătoria trebuie să înceapă într-o regiune care nu este marcată cu un asterisc.

Exemple

folosind problema Konigsberg ca primul său exemplu Euler arată următoarele:

Numărul de poduri = 7, Numărul de poduri plus unu = 8

Regiunea Poduri ori Regiunea trebuie să apară

a 5 3

B 3 2

C 3 2

D 3 2

cu toate acestea, 3 + 2 + 2 + 2 = 9, care este mai mult de 8, deci călătoria este imposibilă.

deoarece acest exemplu este mai degrabă de bază, Euler decide să-și proiecteze propria situație cu două insule, patru râuri și cincisprezece poduri. Situația creată de Euler poate fi văzută în Figura 3 de mai sus. Euler încearcă acum să-și dea seama dacă există o cale care permite cuiva să treacă peste fiecare pod o singură dată. Euler urmează aceiași pași ca mai sus, denumind cele cinci regiuni diferite cu majuscule și creează un tabel pentru a verifica dacă este posibil, cum ar fi următoarele:

Numărul de poduri = 15, Numărul de poduri plus unu = 16

Poduri Regiune ori Regiunea trebuie să apară

A* 8 4

B* 4 2

C* 4 2

D 3 2

E 5 3

f* 6 3

În plus, 4 + 2 + 2 + 2 + 3 + 3 = 16, care este egal cu numărul de poduri, plus unul, ceea ce înseamnă că călătoria este, de fapt, posibilă. Deoarece suma este egală cu numărul de poduri plus unul, călătoria trebuie să înceapă fie în D, fie în E. Acum, că Euler știe că este posibil să facă o călătorie, tot ce trebuie să facă este să precizeze care va fi calea. Euler alege calea EaFbBcFdAeFfCgAhCiDkAmEnApBoElD, unde include Ce poduri sunt traversate între literele care reprezintă masele terestre. Deși aceste informații sunt străine, deoarece podul exact nu contează știind că o călătorie este posibilă, este utilă atunci când selectați o cale. Acesta este un bun exemplu care arată metoda pe care Euler ar folosi-o atunci când rezolvă orice problemă de această natură.

concluziile lui Euler

în următoarele câteva paragrafe, Euler prezintă un alt mod de a afla dacă o călătorie poate fi făcută având în vedere orice set de mase terestre, poduri și râuri. La punctul 16, Euler subliniază că numărul total al numerelor enumerate direct în dreapta maselor terestre se ridică la dublul numărului total de poduri. Acest fapt devine mai târziu cunoscut sub numele de lema de strângere de mână. Practic, lema de strângere de mână afirmă că fiecare pod este numărat de două ori, o dată pentru fiecare masă de teren la care este atașat. La punctul 17, Euler continuă să afirme că suma tuturor podurilor care duc la fiecare regiune este uniformă, deoarece jumătate din acest număr este egal cu numărul total de poduri. Cu toate acestea, acest lucru este imposibil dacă există un număr impar de mase terestre cu un număr impar de poduri. Prin urmare, Euler dovedește că, dacă există unele numere impare atașate maselor terestre, trebuie să existe un număr par de aceste mase terestre.

cu toate acestea, acest lucru nu este suficient pentru a dovedi când există o cale în care fiecare pod este folosit o dată și o singură dată, deoarece problema podului K-Nigsberg are un număr par de mase terestre cu un număr impar de poduri care merg către ele. Din această cauză, Euler adaugă mai multe restricții la punctele 18 și 19. Euler explică faptul că, din moment ce numărul total de poduri atașate fiecărei mase terestre este egal cu dublul numărului de poduri (așa cum se vede în lema de strângere de mână), deci, dacă adăugați două la această sumă și apoi împărțiți la două, veți obține numărul de poduri totale plus unul. Acest număr este același cu cel folosit anterior, care este folosit pentru a spune dacă este posibilă o cale. Dacă toate numerele sunt uniforme, atunci a treia coloană din tabel va însuma cu una mai mică decât numărul total de poduri plus una.

Euler explică apoi că este evident că dacă există două mase terestre cu un număr impar de poduri, călătoria va fi întotdeauna posibilă dacă călătoria începe într-una din regiunile cu un număr impar de poduri. Acest lucru se datorează faptului că, dacă numerele pare sunt înjumătățite și fiecare dintre cele impare este mărită cu una și înjumătățită, suma acestor jumătăți va fi egală cu una mai mult decât numărul total de poduri. Cu toate acestea, dacă există patru sau mai multe mase terestre cu un număr impar de poduri, atunci este imposibil să existe o cale. Acest lucru se datorează faptului că suma jumătăților numerelor impare plus unu împreună cu suma tuturor jumătăților numerelor pare vor face ca suma celei de-a treia coloane să fie mai mare decât numărul total de poduri plus unu. Prin urmare, Euler tocmai a dovedit că pot exista cel mult două mase terestre cu un număr impar de poduri.

cu acest lucru fiind declarat, Euler poate face acum concluziile sale cu privire la forme mai generale ale problemei podului K-Nigsberg. În paragraful 20, Euler oferă cele trei linii directoare pe care cineva le poate folosi pentru a afla dacă există o cale folosind fiecare pod o singură dată. În primul rând, el a susținut că dacă există mai mult de două mase terestre cu un număr impar de poduri, atunci nu este posibilă o astfel de călătorie. În al doilea rând, dacă numărul de poduri este impar pentru exact două mase terestre, atunci călătoria este posibilă dacă începe într-una din cele două mase terestre numerotate impare. În cele din urmă, Euler afirmă că, dacă nu există regiuni cu un număr impar de mase terestre, atunci călătoria poate fi realizată începând din orice regiune. După ce a afirmat aceste trei fapte, Euler își încheie dovada cu paragraful 21, care afirmă pur și simplu că, după ce cineva își dă seama că există o cale, ei trebuie să treacă prin efortul de a scrie o cale care funcționează. Euler credea că metoda de a realiza acest lucru era banală și nu dorea să petreacă mult timp pe ea. Cu toate acestea, Euler a sugerat să se concentreze asupra modului de a ajunge de la o masă terestră la alta, în loc să se concentreze la început pe podurile specifice.

dovada lui Euler și teoria grafurilor

când citim dovada originală a lui Euler, descoperim o lucrare matematică relativ simplă și ușor de înțeles; cu toate acestea, nu este dovada reală, ci pașii intermediari care fac această problemă faimoasă. Marea inovație a lui Euler a fost în vizualizarea abstractă a problemei podului K. Nigsberg, folosind linii și litere pentru a reprezenta situația mai largă a maselor terestre și a podurilor. El a folosit majuscule pentru a reprezenta mase terestre și litere mici pentru a reprezenta poduri. Acesta a fost un tip de gândire complet nou pentru acea vreme, iar în lucrarea sa, Euler a declanșat accidental o nouă ramură a matematicii numită Teoria grafurilor, unde un grafic este pur și simplu o colecție de vârfuri și margini. Astăzi, o cale dintr-un grafic, care conține fiecare margine a graficului o singură dată, se numește cale Euleriană, din cauza acestei probleme. Din momentul în care Euler a rezolvat această problemă până astăzi, teoria grafurilor a devenit o ramură importantă a matematicii, care ghidează baza gândirii noastre despre rețele.

problema podului K-ului este motivul pentru care Biggs afirmă,

originile teoriei grafurilor sunt umile, chiar frivole … problemele care au dus la dezvoltarea teoriei grafurilor au fost adesea puțin mai mult decât puzzle-uri, concepute pentru a testa ingeniozitatea, mai degrabă decât pentru a stimula imaginația. Dar, în ciuda aparentei trivialități a unor astfel de puzzle-uri, acestea au captat interesul matematicienilor, astfel încât teoria grafurilor a devenit un subiect bogat în rezultate teoretice de o varietate și profunzime surprinzătoare.

după cum ar sugera afirmația lui Biggs, această problemă este atât de importantă încât este menționată în primul capitol al fiecărei cărți de teorie a grafurilor care a fost citită în bibliotecă.

după descoperirea lui Euler (sau invenție, în funcție de modul în care cititorul o privește), teoria grafurilor a explodat cu contribuții majore aduse de mari matematicieni precum Augustin Cauchy, William Hamilton, Arthur Cayley, Gustav Kirchhoff și George Polya. Toți acești oameni au contribuit la descoperirea „aproape tot ceea ce se știe despre graficele mari, dar ordonate, cum ar fi rețeaua formată din atomi într-un cristal sau rețeaua hexagonală făcută de albine într-un stup .”Alte probleme celebre ale teoriei grafurilor includ găsirea unei modalități de a scăpa dintr-un labirint sau labirint sau găsirea ordinii mișcărilor cu un cavaler pe o tablă de șah, astfel încât fiecare pătrat să fie aterizat o singură dată și cavalerul să se întoarcă în spațiul pe care a început . Unele alte probleme ale teoriei grafurilor au rămas nerezolvate de secole .

soarta lui K-Nigsberg

în timp ce teoria grafurilor a explodat după ce Euler a rezolvat problema podului K-Nigsberg, orașul K-Nigsberg a avut o soartă mult diferită. În 1875, oamenii din K. Nigsberg au decis să construiască un nou pod, între nodurile B și C, mărind numărul de legături ale acestor două mase terestre la patru. Aceasta a însemnat că doar două mase terestre aveau un număr impar de legături, ceea ce a dat o soluție destul de simplă problemei. Crearea podului suplimentar poate sau nu să fi fost cauzată subconștient de dorința unei căi de rezolvare a celebrei probleme a orașului.

cu toate acestea, un nou pod nu a rezolvat toate problemele viitoare ale lui K-Nigsberg, deoarece orașul nu se aștepta în secolul al XIX-lea, „soarta tristă și sfâșiată de război care o aștepta ca gazdă pentru una dintre cele mai înverșunate bătălii din al doilea război mondial.”Timp de patru zile, în August 1944, bombardierele britanice au distrus atât orașul vechi, cât și părțile nordice ale K-ului. În ianuarie și februarie 1945, regiunea care înconjoară K-Ulnigsberg este înconjurată de forțele rusești. Civilii germani încep să evacueze din oraș, dar se mișcă prea târziu. Mii de oameni sunt uciși încercând să fugă cu barca și pe jos peste apele înghețate ale lagunei Curoniene. În aprilie 1945, Armata Roșie capturează K-Ulnigsberg cu aproximativ nouăzeci la sută din orașul vechi zăcând în ruine.

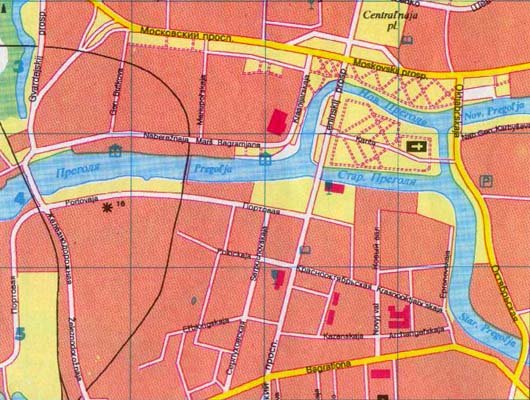
o hartă stradală curentă A K-ului K-Nigsberg este prezentată mai jos . Această hartă arată cât de mult sa schimbat orașul. Multe dintre poduri au fost distruse în timpul bombardamentelor, iar orașul nu mai poate pune aceeași întrebare interesantă pe care au putut-o în secolul al XVIII-lea. Împreună cu un aspect foarte diferit, orașul K. Nigsberg are un nou nume, Kaliningrad, cu râul Pregel redenumit Pregolya . În timp ce soarta lui K-Nigsberg este teribilă, vechea problemă a cafenelei cetățenilor de a traversa fiecare dintre cele șapte poduri vechi exact o singură dată a dus la formarea unei ramuri complet noi a matematicii, teoria grafurilor.

Biggs, Norman L., E. K. Lloyd și Robin J. Wilson. Teoria Grafurilor: 1736-1936. Oxford: Clarendon Press, 1976.

Dunham, William. Euler: stăpânul nostru, al tuturor. Washington: Asociația matematică a Americii, 1999.

Euler, Leonhard, ‘Solutio problematis ad geometriam situs pertinentis’ (1741), Enestr 53, Maa Euler Archive.

„Istoria matematicii: despre Leonhard Euler (1707-1783).”ScienceWeek (2003). 6 noiembrie. 2005.Hopkins, Brian și Robin Wilson. „Adevărul despre K-Nigsberg.”College Mathematics Journal (2004), 35, 198-207.

„Poduri Konigsberg.”Istoria MacTutor de matematică Arhiva:
http://www-history.mcs.st- and.ac.uk/history/Miscellaneous/other_links/Konigsberg.html

Nota editorului: Acest articol a fost publicat inițial în convergență, Volumul 3 (2006).