2.5: fluxul Legii lui Darcy într-un mediu poros
legea lui Darcy este crucială pentru înțelegerea multor ramuri ale geologiei, în special a hidrogeologiei. Înainte de a ne uita la lege și ce ne poate spune, să ne uităm la modul în care a fost dezvoltată. Legea lui Darcy este numită după Henry Darcy, un inginer francez din secolul al 19-lea care a dezvoltat un sistem subteran de conducte sub presiune pentru a furniza apă în jurul orașului Dijon. Sistemul, care a furnizat și apă faimoaselor fântâni Dijon, a revoluționat sistemele de apă și canalizare ale orașului. Sistemul nu a necesitat Pompe și a fost condus exclusiv de gravitație. În timpul procesului de dezvoltare a noului sistem, Darcy a efectuat o serie de experimente în care a încercat să miște apa folosind exclusiv gravitația.
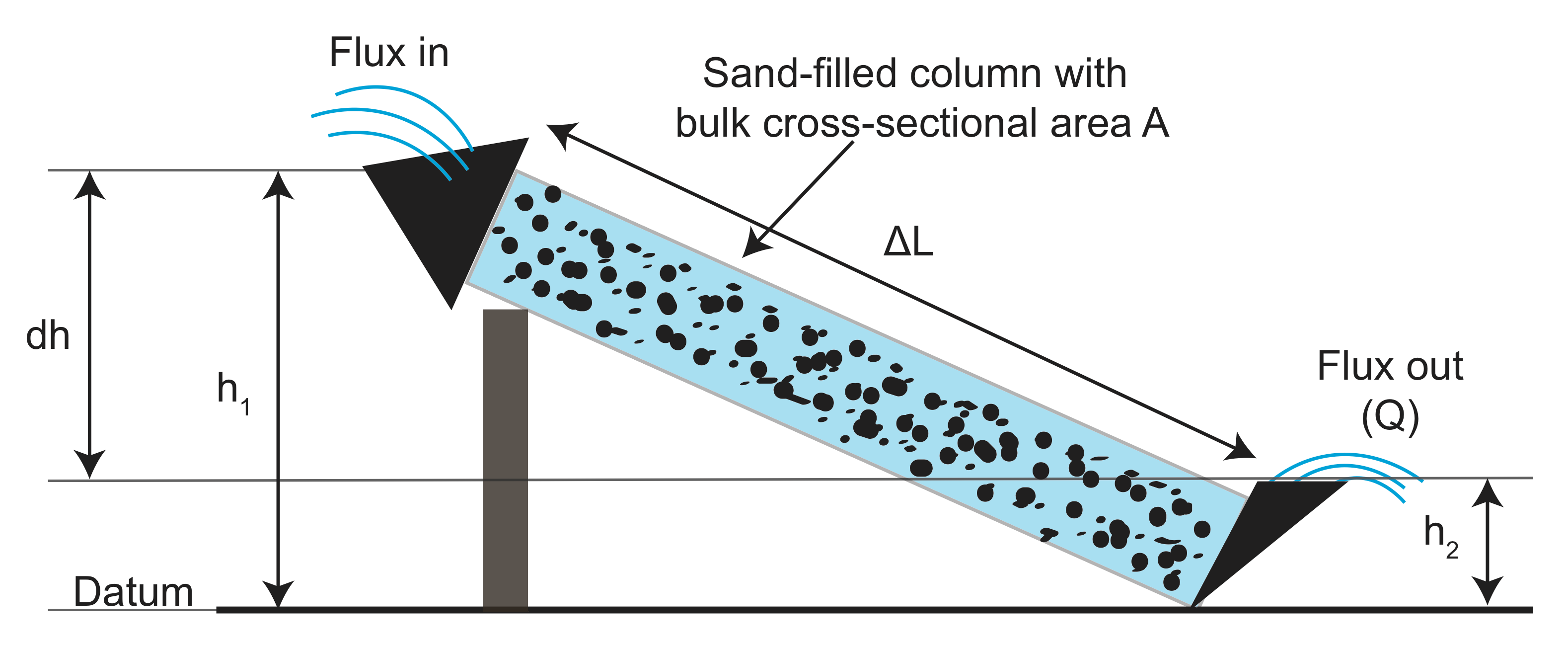
Din experimente, au fost colectate date despre lungimea canalului (\(l\)), aria secțiunii transversale a canalului (\(A\)), diferența de înălțime (\(h_1 – h_2\)) și fluxul de apă care iese \(Q\) atât cu, cât și fără material granular (filtrant) în Flume. Apoi a trasat măsurarea fluxului normalizată de zonă față de raportul dintre diferența de înălțime și lungimea canalului (\( \frac{h_1 – h_2}{l}\)). Ceea ce a descoperit este că există o relație liniară, iar panta depinde de materialul granular pe care l-a folosit în canal:
\
care poate fi rescris ca derivat,
\
unde \(K\) este conductivitatea hidraulică și \(\frac{dh}{dx}\) este gradientul hidraulic. \(Q\), rata totală de descărcare de gestiune, are unități de \(\frac{m^3}{s}\), Volumul de apă pe timp. Semnul negativ se datorează faptului că fluidul curge în jos (negativ) gradientul hidraulic de la valori mai mari la valori mai mici.conductivitatea hidraulică este un parametru fizic care explică cât de ușor se poate deplasa fluidul prin spațiul porilor pentru material. În experimentele originale ale lui Darcy, el a folosit nisipuri cu dimensiuni diferite ale granulelor, cu toate acestea, conductivitatea hidraulică poate fi determinată și pentru rocile solide, deoarece majoritatea rocilor au un spațiu al porilor.
În urma experimentelor originale ale lui Darcy, s-au făcut lucrări suplimentare pentru a înțelege proprietățile fizice ale fluidului și rocii care determină conductivitatea hidraulică eficientă. Din aceste experimente s-a constatat că,
\
unde \(k\) este permeabilitatea intrinsecă a mediului poros (solidul), \(\ETA\) este vâscozitatea dinamică a fluidului și \(\gamma = \rho G\) este greutatea specifică a fluidului, care depinde de densitatea fluidului, \(\rho\) și gravitația, \(g\).
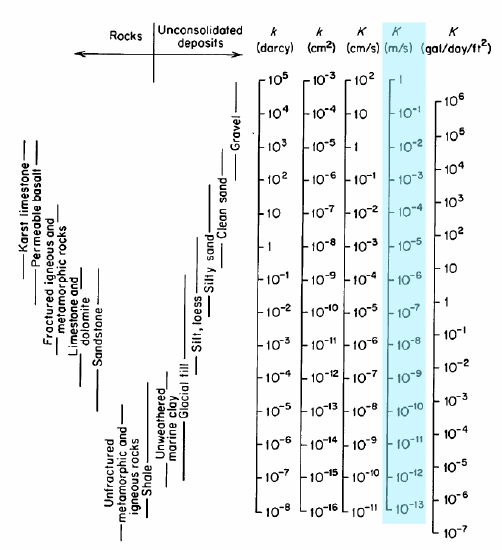
coloana evidențiată din figură este K, conductivitatea hidraulică în \(\frac{m}{s}\); acestea sunt unitățile pe care le vom folosi. Conductivitatea hidraulică este, de asemenea, uneori raportată în termeni de permeabilitate intrinsecă, \(k\), cu unități de darcys sau cm2. Gama completă de valori pentru conductivitatea hidraulică este 1-10-13 \(\frac{m}{s}\). Experimente precum Darcy sunt folosite pentru a măsura K în materiale reale.
rata de descărcare \(q\) este un flux de volum (\(m^3/S\)), dar de obicei ne gândim la fluxul de fluid în termeni de viteză sau viteză. Întrebările de descărcare pot fi rearanjate prin împărțirea prin zonă pentru a defini fluxul Darcy
\\]
sau în termeni de permeabilitate intrinsecă și gradient de presiune,
\
unde \(\eta\) este vâscozitatea fluidului (vezi mai jos pentru derivarea celei de-a doua ecuații).
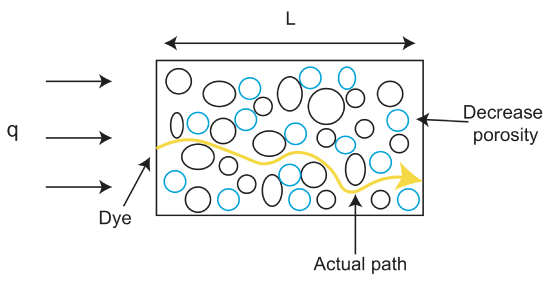
este important să rețineți că fluxul Darcy nu este egal cu viteza fluidului, chiar dacă este în unități de viteză. Viteza fluidului se găsește prin Viteza liniară medie (\(v_a\)), care este medie a vitezei tuturor căilor posibile ale fluidului prin mediul poros: dar găsirea acestei valori este în afara domeniului de aplicare al acestei clase. În schimb, vom observa că viteza fluidului este
\
unde \(\varphi\) este porozitatea și v este viteza fluidului. Porozitatea, \(\varphi\) este calculată ca raport între volumul spațiului gol și volumul total al unui material \(\varphi=\frac{V_{void}}{V_{tot}}\), și este de obicei exprimată ca o fracție între 0 și 1 sau ca procent. Rețineți că dacă \ (\varphi \ leq\) 1 atunci viteza fluidului este mai mare fluxul darcy.
un alt termen care apare atunci când se discută fluxul prin roci și materiale neconsolidate este permeabilitatea. În timp ce porozitatea este fracțiunea reală a porilor (golurilor) din rocă, aceste goluri pot avea forme diferite și conectivitate diferită, ceea ce afectează cât de ușor se poate deplasa un fluid prin spațiul porilor. Permeabilitatea este o măsură a ușurinței cu care lichidele și gazele pot trece printr-o piatră. Cu cât materialul este mai consolidat, cu atât permeabilitatea acestuia este mai mică. Astfel, materialele „libere” precum pietrișul au o permeabilitate ridicată. Unele roci pot avea, de asemenea, permeabilitate anizotropă, ceea ce înseamnă că fluidele pot curge cu ușurință într-o direcție, dar nu în alta. Un exemplu de rocă cu permeabilitate anizotropă este un șist. Fluidele se pot deplasa cu ușurință într-un strat de șist, dar nu se pot deplasa peste straturi.
viteza fluidului
să facem un exemplu de bază.
ni se dă că \(q=2\frac{m}{min}\) și \(\varphi\) este de 25% și doriți să găsiți viteza fluidului.
convertim mai întâi 25% la 0,25.
atunci, \(v=\frac{2}{0.25} \ frac{m}{min}\)
și
\(v=8 \frac{m}{min}\) este viteza fluidului.
cap hidraulic
revenind la experimentele lui Darcy, ceea ce este procesul fizic este de fapt de conducere fluxul de lichid prin canal?
termenul \(\frac{dh}{dx} \) este denumit cap hidraulic, care este presiunea lichidului datorată greutății unui fluid în raport cu o anumită locație de referință: un gradient de presiune. Cu toate acestea, \(\frac{dh}{DX} \) nu are unități de presiune pe unitate de lungime, deci de ce se numește cap hidraulic?
Să analizăm care este presiunea în canalul din experimentele lui Darcy. Pentru a face experimentele, Darcy a avut un rezervor de apă la capătul de sus al canalului oferind un nivel constant de apă în partea de sus a canalului, echivalent cu înălțimea canalului, \(h_1\). În mod similar, a existat un rezervor în partea de jos cu un nivel constant de apă echivalent cu \(h_2\). Prin urmare, presiunea fluidului din fiecare rezervor datorită greutății apei este dată de \(P = \rho g h\). Gradientul de presiune dintre partea de sus și partea de jos a penei este apoi
\
sau
\
substituind în Legea lui Darcy,
\ &=\frac{K}{\rho g}\frac{dp}{DX} \end{align}. \]
Reamintim, de sus că conductivitatea hidraulică poate fi scrisă în termeni de permeabilitate intrinsecă ca\(K = k\frac {\gamma} {\ETA}\) care este echivalent cu\(k\frac {\rho g} {\ETA}\) sau rearanjare, \(\frac{K} {\rho g} = \frac{k} {\eta}\). Prin urmare, putem substitui pentru a da două expresii echivalente pentru Legea lui Darcy, cu un interior al gradientului în înălțime,
\
și al doilea în termeni de gradient în presiune,
astfel,\(\frac{dh}{dx}\) se numește cap hidraulic deoarece originea fizică a termenului în Legea lui Darcy este gradientul de presiune din fluid, care conduce fluxul.
apa care părăsește un acvifer
să facem acum un exemplu calculând viteza fluidului apei care intră într-un acvifer. În schița de sub înălțimea acviferului urmează topografia de pe dealul adiacent văii cu pârâul. Apa curge de la presiune înaltă (înălțimea capului) spre vale și lasă acviferul la pârâu. Putem folosi legea lui Darcy pentru a estima rata debitului de apă din acvifer.
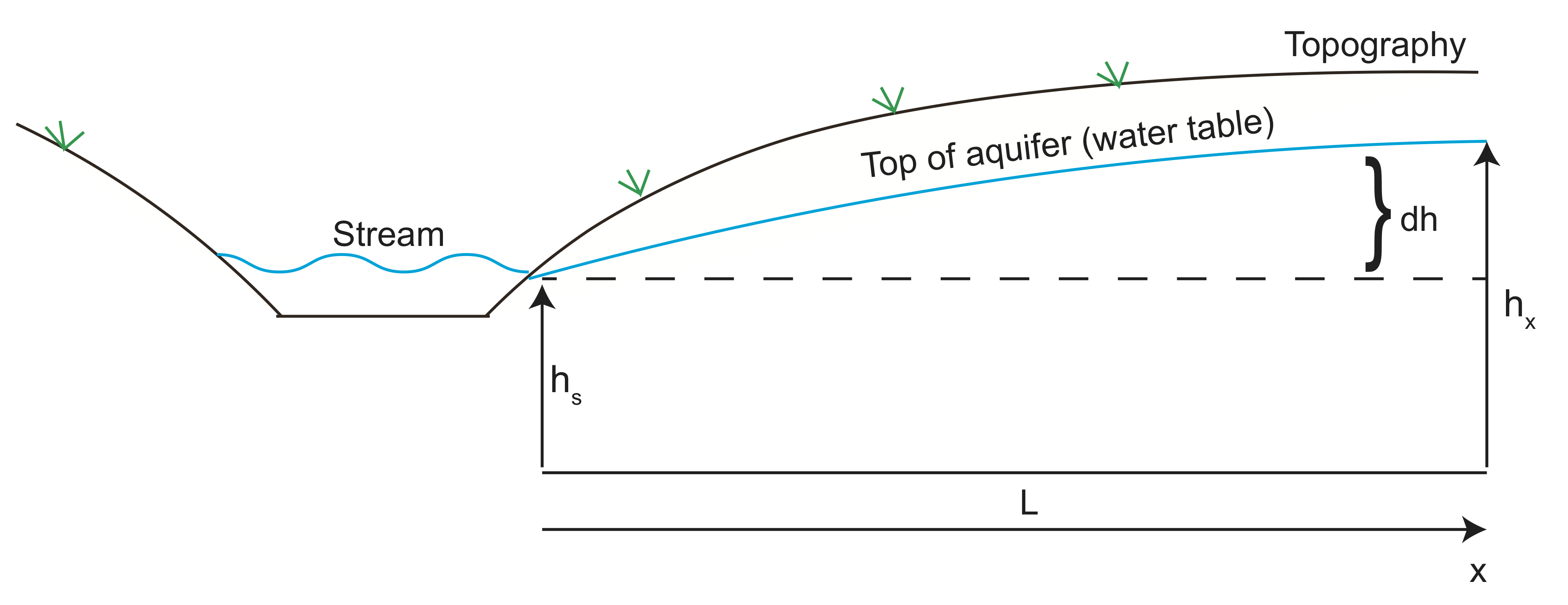
folosind imagistica geofizică, înălțimea acviferului se dovedește a fi de 10 m (\(dh\)) deasupra înălțimii pârâului la aproximativ 100 de metri (\(l\)) distanță. Să presupunem că conductivitatea hidraulică este \ (K=10 ^ {-6}\) m/s și porozitatea este \(\varphi=30\)%.
fluxul darcy este
\
\
viteza fluidului este
\

flux Laminar versus flux Turbulent
una dintre ipotezele implicite din Legea lui Darcy este că fluxul este laminar. Fluxul Laminar este caracterizat ca fiind format din straturi subțiri sau lamele de fluid care se deplasează paralel unul cu celălalt. În schimb, fluxul turbulent se caracterizează prin vârtejuri, vârtejuri și vârtejuri, în care straturile adiacente de fluid diferă și iau diferite căi în jos.
o modalitate prin care putem cuantifica dacă un fluid este laminar sau turbulent este prin calcularea numărului lui Reynold pentru flux, definit ca
\
numărul lui Reynold se găsește luând în considerare cei doi termeni din echilibrul impulsului pentru flux. Primul termen este forța inerțială pe unitatea de volum, care conduce fluxul, \ (\rho u \ frac{du}{dx}\). Al doilea termen este forța vâscoasă pe unitate de volum, care rezistă fluxului, \(\eta\frac{d^2U}{DX^2}\). Acești doi termeni trebuie să echilibreze, astfel încât să le putem seta egal,
\
apoi, vom rescrie Termenii, într-un mod simplificat pentru a capta doar dimensiunile relevante ale variabilelor. Pentru a face, parcurgem ceea ce se numește analiză dimensională, în care înlocuim fiecare variabilă, cu o valoare de referință, ori o formă non-dimensională a variabilei.
de exemplu, termenul \(x\) este rescris ca doar \(L x’\), unde \(L\) este lungimea de referință (adâncimea fluidului) și \(x’\) este distanța nedimensională. În mod similar, lăsăm \(u = u_o u’\). Substituindu-le în ecuație, obținem
\
apoi combinăm valorile constante din față
\
rețineți că combinația variabilelor din față este numărul lui Reynold
\
unde variabilele sunt \(u_o\) viteza de curgere, l adâncimea fluidului și variabilele pe care le-am văzut mai devreme, \(\rho\) densitatea fluidului și \(\ETA\) vâscozitatea fluidului. Parcurgând această analiză, constatăm că orice flux care se caracterizează prin echilibrul acestor doi termeni poate fi comparat prin simpla cunoaștere a valorii numărului lui Reynolds. De exemplu, dacă un flux are o vâscozitate care este de 10 ori vâscozitatea într-un alt flux, cele două fluxuri se vor comporta la fel este densitatea (sau viteza sau lungimea) este, de asemenea, crescută cu un factor de 10 pentru cazul de vâscozitate mai mare; adică numărul Reynolds pentru cele două fluxuri este același.
pentru a avea fluxul Darcy, numărul lui Reynold trebuie să fie mai mic de aproximativ 1-10 (laminar). Pentru \(Re >1-10 \) fluxul nu este strict laminar, dar nu este încă turbulent (neliniar, nu-laminar). Pentru a avea un flux turbulent, numărul lui Reynold trebuie să fie mai mare de aproximativ 2000.
înțelegerea faptului că constantele din numărător și numitor afectează caracteristicile fluxului în mod opus, ajută, de asemenea, să se gândească la modul în care fluidele diferite se vor comporta în condiții externe similare. De exemplu, un fluid mai dens, care are, de asemenea, o viteză rapidă va avea o Re mai mare și prezintă un comportament turbulent. În schimb, un fluid precum gheața care are o vâscozitate ridicată și se mișcă foarte încet va avea o Re scăzută și va avea probabil flux laminar. Vâscozitatea ridicată a gheții acționează pentru stabilizarea fluxului. Ca un alt exemplu, considerăm că două fluide ar putea fi ambele în mișcare la aceeași viteză se comportă diferit dacă celelalte valori din numărul lui Reynold \(\frac{\rho l}{\mu}\) sunt diferite. Prin urmare, tipul de flux depinde nu numai de viteza de curgere, ci și de combinația de variabile din numărul lui Reynold.
aplicarea fluxului lui Darcy
legea lui Darcy este ecuația principală care guvernează fluxul în acvifere și puțuri. Fără ea, nu am fi capabili să forăm puțuri sau să înțelegem mișcarea apei în acvifere, în special în valea centrală a Californiei, unde ambele idei sunt cruciale atât pentru productivitatea agricolă, cât și pentru scăderea apelor subterane.
