La regresión a la media es un fenómeno estadístico común que puede engañarnos cuando observamos el mundo. Aprender a reconocer cuándo está en juego la regresión a la media puede ayudarnos a evitar malinterpretar datos y ver patrones que no existen.

* * *

Es importante minimizar los casos de mal juicio y abordar los puntos débiles en nuestro razonamiento. Aprender sobre la regresión a la media puede ayudarnos.

El psicólogo ganador del premio Nobel Daniel Kahneman escribió un libro sobre prejuicios que nublan nuestro razonamiento y distorsionan nuestra percepción de la realidad. Resulta que hay todo un conjunto de errores lógicos que cometemos porque nuestra intuición y nuestro cerebro no manejan bien las estadísticas simples. Uno de los errores que examina al Pensar Rápido y Lento es la infame regresión hacia la media.

La noción de regresión a la media fue elaborada por primera vez por Sir Francis Galton. La regla es que, en cualquier serie con fenómenos complejos que dependen de muchas variables, donde el azar está involucrado, los resultados extremos tienden a ser seguidos por otros más moderados.

En Seeking Wisdom, Peter Bevelin ofrece el ejemplo de John, que no estaba satisfecho con el rendimiento de los nuevos empleados, por lo que los puso en un programa de mejora de habilidades donde midió las habilidades de los empleados:

Sus puntuaciones ahora son más altas que en la primera prueba. La conclusión de John: «El programa de mejora de habilidades causó la mejora en las habilidades.»Esto no es necesariamente cierto. Sus puntajes más altos podrían ser el resultado de la regresión a la media. Dado que se midió que estos individuos se encontraban en el extremo inferior de la escala de habilidades, habrían mostrado una mejora incluso si no hubieran tomado el programa de mejora de habilidades. Y podría haber muchas razones para su rendimiento anterior: estrés, fatiga, enfermedad, distracción, etc. Su verdadera capacidad tal vez no ha cambiado.

Nuestro rendimiento siempre varía en torno a un rendimiento real promedio. El rendimiento extremo tiende a ser menos extremo la próxima vez. ¿Por qué? Las mediciones de prueba nunca pueden ser exactas. Todas las mediciones se componen de una parte verdadera y una parte de error aleatorio. Cuando las mediciones son extremas, es probable que sean causadas en parte por el azar. Es probable que la probabilidad contribuya menos la segunda vez que medimos el rendimiento.

Si cambiamos de una forma de hacer algo a otra simplemente porque no tenemos éxito, es muy probable que lo hagamos mejor la próxima vez, incluso si la nueva forma de hacer algo es igual o peor.

Esta es una de las razones por las que es peligroso extrapolar muestras de tamaños pequeños, ya que los datos pueden no ser representativos de la distribución. También es por eso que James March argumenta que cuanto más tiempo permanezca alguien en su trabajo, «menor será la diferencia probable entre el registro observado de rendimiento y la capacidad real.»Cualquier cosa puede suceder a corto plazo, especialmente en cualquier esfuerzo que implique una combinación de habilidad y suerte. (La relación entre habilidad y suerte también afecta la regresión a la media.)

Regresión a la Media

Los efectos de la regresión a la media se pueden observar con frecuencia en los deportes, donde el efecto causa muchas especulaciones injustificadas.

Pensando Rápido y lento, Kahneman recuerda ver el salto de esquí para hombres, una disciplina donde la puntuación final es una combinación de dos saltos separados. Consciente de la regresión a la media, Kahneman se sorprendió al escuchar las predicciones del comentarista sobre el segundo salto. Escribe:

Noruega tuvo un gran primer salto; estará tenso, esperando proteger su ventaja y probablemente lo hará peor» o «Suecia tuvo un mal primer salto y ahora sabe que no tiene nada que perder y estará relajado, lo que debería ayudarlo a hacerlo mejor.

Kahneman señala que el comentarista había notado la regresión a la media y se le ocurrió una historia para la que no había evidencia causal (ver falacia narrativa). Esto no quiere decir que su historia no pudiera ser cierta. Tal vez, si medimos las frecuencias cardíacas antes de cada salto, veríamos que están más relajadas si el primer salto fue malo. Sin embargo, ese no es el punto. El punto es que la regresión a la media ocurre cuando la suerte juega un papel, como lo hizo en el resultado del primer salto.

La lección de deportes se aplica a cualquier actividad en la que el azar juega un papel. A menudo adjuntamos explicaciones de nuestra influencia sobre un proceso en particular al progreso o la falta de él.

En realidad, la ciencia del rendimiento es compleja, depende de la situación y, a menudo, gran parte de lo que creemos que está bajo nuestro control es verdaderamente aleatorio.

En el caso de los saltos de esquí, un fuerte viento contra el saltador hará que incluso el mejor atleta muestre resultados mediocres. Del mismo modo, un fuerte viento y condiciones de esquí a favor de un saltador mediocre pueden llevar a un aumento considerable, pero temporal, en sus resultados. Estos efectos, sin embargo, desaparecerán una vez que las condiciones cambien y los resultados vuelvan a la normalidad.

Esto puede tener serias implicaciones para el entrenamiento y el seguimiento del rendimiento. Las reglas de regresión sugieren que al evaluar el desempeño o la contratación, debemos confiar en los registros de seguimiento más que en los resultados de situaciones específicas. De lo contrario, somos propensos a sentirnos decepcionados.

Cuando Kahneman estaba dando una conferencia a la Fuerza Aérea Israelí sobre la psicología del entrenamiento efectivo, uno de los oficiales compartió su experiencia de que extender elogios a sus subordinados llevó a un peor rendimiento, mientras que regañar llevó a una mejora en los esfuerzos posteriores. Como consecuencia, se había vuelto generoso con los comentarios negativos y se había vuelto bastante cauteloso de dar demasiados elogios.

Kahneman inmediatamente se dio cuenta de que era una regresión a la media en el trabajo. Ilustró el concepto erróneo con un simple ejercicio que tal vez desee probar usted mismo. Dibujó un círculo en una pizarra y luego pidió a los oficiales uno por uno que arrojaran un trozo de tiza al centro del círculo con la espalda hacia la pizarra. Luego repitió el experimento y registró la actuación de cada oficial en el primer y segundo juicio.

Naturalmente, aquellos que lo hicieron increíblemente bien en el primer intento tendieron a hacerlo peor en su segundo intento y viceversa. La falacia se hizo evidente de inmediato: el cambio en el rendimiento ocurre naturalmente. De nuevo, eso no quiere decir que los comentarios no importen en absoluto, tal vez sí, pero el oficial no tenía pruebas para concluir que sí.

La Correlación imperfecta y el Azar

En este punto, es posible que se pregunte por qué ocurre la regresión a la media y cómo podemos asegurarnos de que somos conscientes de ello cuando ocurre.

Para entender la regresión a la media, primero debemos entender la correlación.

El coeficiente de correlación entre dos medidas que varía entre -1 y 1, es una medida del peso relativo de los factores que comparten. Por ejemplo, dos fenómenos con pocos factores compartidos, como el consumo de agua embotellada versus la tasa de suicidio, deberían tener un coeficiente de correlación cercano a 0. Es decir, si nos fijamos en todos los países del mundo y se representan las tasas de suicidio de un año específico contra el consumo per cápita de agua embotellada, la parcela no muestran ningún patrón.

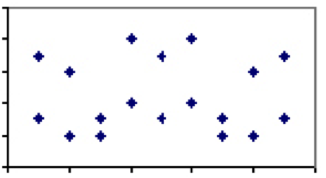
Por el contrario, hay medidas que son exclusivamente de dependencia en el mismo factor. Un buen ejemplo de esto es la temperatura. El único factor que determina la temperatura – la velocidad de las moléculas — es compartido por todas las escalas, por lo tanto, cada grado en Celsius tendrá exactamente un valor correspondiente en Fahrenheit. Por lo tanto, la temperatura en grados Celsius y Fahrenheit tendrá un coeficiente de correlación de 1 y la gráfica será una línea recta.

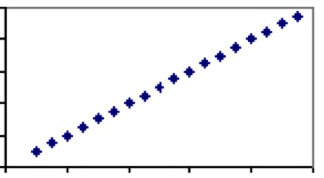
Hay pocos, si alguno, de los fenómenos de las ciencias humanas que tienen un coeficiente de correlación de 1. Sin embargo, hay muchos en los que la asociación es de débil a moderada y hay un cierto poder explicativo entre los dos fenómenos. Considere la correlación entre la altura y el peso, que aterrizaría en algún lugar entre 0 y 1. Mientras que prácticamente cada niño de tres años será más ligero y más bajo que cada hombre adulto, no todos los hombres adultos o niños de tres años de la misma altura pesarán lo mismo.

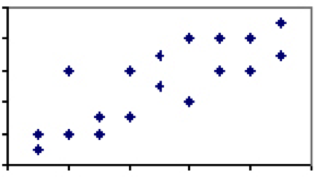
Esta variación y el correspondiente menor grado de correlación implica que, si bien la altura es en general un buen predictor, claramente hay otros factores que no son la altura en juego. Cuando la correlación de dos medidas es menos que perfecta, debemos tener cuidado con los efectos de la regresión a la media.

Kahneman observó una regla general: Siempre que la correlación entre dos puntuaciones sea imperfecta, habrá regresión a la media.

Esto al principio puede parecer confuso y no muy intuitivo, pero el grado de regresión a la media está directamente relacionado con el grado de correlación de las variables. Este efecto se puede ilustrar con un ejemplo sencillo.

Asuma que está en una fiesta y pregunte por qué es que las mujeres altamente inteligentes tienden a casarse con hombres que son menos inteligentes de lo que son. La mayoría de las personas, incluso las que tienen algún entrenamiento en estadísticas, se lanzarán rápidamente con una variedad de explicaciones causales que van desde evitar la competencia hasta los temores de soledad que enfrentan estas mujeres. Es probable que un tema de tal controversia suscite un gran debate.

Ahora, ¿y si preguntamos por qué la correlación entre las puntuaciones de inteligencia de los cónyuges es menos que perfecta? Esta pregunta no es tan interesante y hay poco que adivinar, todos sabemos que es verdad. La paradoja radica en el hecho de que las dos preguntas resultan ser algebraicamente equivalentes. Kahneman explica:

Si la correlación entre la inteligencia de los cónyuges es menos que perfecta (y si los hombres y las mujeres en promedio no difieren en inteligencia), entonces es una inevitabilidad matemática que las mujeres altamente inteligentes se casen con esposos que en promedio son menos inteligentes que ellos (y viceversa, por supuesto). La regresión observada a la media no puede ser más interesante o explicable que la correlación imperfecta.

Suponiendo que la correlación es imperfecta, las posibilidades de que dos socios representen el 1% superior en términos de cualquier característica es mucho menor que un socio que represente el 1% superior y el otro, el 99% inferior.

La Causa, el Efecto y el Tratamiento

Debemos ser especialmente cautelosos con la regresión al fenómeno medio al tratar de establecer la causalidad entre dos factores. Siempre que la correlación sea imperfecta, lo mejor siempre parecerá empeorar y lo peor parecerá mejorar con el tiempo, independientemente de cualquier tratamiento adicional. Esto es algo que los medios de comunicación en general y a veces incluso los científicos capacitados no reconocen.

Considere el ejemplo que Kahneman da:

Los niños deprimidos tratados con una bebida energética mejoran significativamente en un período de tres meses. Inventé este titular de periódico, pero el hecho de que informa es cierto: si trató a un grupo de niños deprimidos durante algún tiempo con una bebida energética, mostrarían una mejoría clínicamente significativa. También es el caso de los niños deprimidos que pasan algún tiempo de pie sobre su cabeza o abrazan a un gato durante veinte minutos al día también mostrarán mejoría.

Siempre que se encuentre con estos titulares, es muy tentador llegar a la conclusión de que las bebidas energéticas, pararse sobre la cabeza o abrazar a los gatos son curas perfectamente viables para la depresión. Estos casos, sin embargo, encarnan una vez más la regresión a la media:

Los niños deprimidos son un grupo extremo, están más deprimidos que la mayoría de los demás niños, y los grupos extremos regresan a la media con el tiempo. La correlación entre los puntajes de depresión en ocasiones sucesivas de pruebas es menos que perfecta, por lo que habrá regresión a la media: los niños deprimidos mejorarán un poco con el tiempo, incluso si no abrazan a los gatos y no beben Red Bull.

A menudo atribuimos erróneamente una política o tratamiento específico como la causa de un efecto, cuando el cambio en los grupos extremos habría ocurrido de todos modos. Esto plantea un problema fundamental: ¿cómo saber si los efectos son reales o simplemente debidos a la variabilidad?

Afortunadamente hay una manera de decir entre una mejora real y una regresión a la media. Se trata de la introducción del denominado grupo de control, que se espera que mejore únicamente mediante regresión. El objetivo de la investigación es determinar si el grupo tratado mejora más de lo que la regresión puede explicar.

En situaciones de la vida real con el desempeño de individuos o equipos específicos, donde el único punto de referencia real es el desempeño pasado y no se puede introducir ningún grupo de control, los efectos de la regresión pueden ser difíciles, si no imposibles, de desenredar. Podemos comparar con el promedio de la industria, los pares en el grupo de cohortes o las tasas históricas de mejora, pero ninguna de estas son medidas perfectas.

***

Afortunadamente, el conocimiento de la regresión al fenómeno medio en sí ya es un gran primer paso hacia un enfoque más cuidadoso para comprender la suerte y el rendimiento.

Si hay algo que aprender de la regresión a la media es la importancia de los registros de seguimiento en lugar de confiar en historias de éxito únicas. Espero que la próxima vez que se encuentre con una calidad extrema en parte gobernada por el azar, se dé cuenta de que es probable que los efectos retrocedan con el tiempo y ajuste sus expectativas en consecuencia.

Qué leer a continuación

• Actualice su pensamiento con 113 modelos mentales explicados.
• Lea sobre el Pensamiento de Segundo Nivel para evitar consecuencias negativas.