En este tutorial, aprenderemos sobre el Puente de Wheatstone. Veremos el principio de funcionamiento del puente Wheatstone, algunos circuitos de ejemplo y algunas aplicaciones importantes.

Introducción al puente de Wheatstone

En el mundo real nos encontramos con varias señales, algunas de ellas se miden por cambios en la resistencia y otras con inductancia y capacitancia.

Si consideramos la resistencia, la mayoría de los sensores industriales como temperatura, deformación, humedad, desplazamiento, nivel de líquido, etc. produce el cambio en el valor de la resistencia para un cambio de variable. Por lo tanto, es necesario un acondicionamiento de señal para cada sensor de resistencia.

Generalmente, la medición de resistencia se divide en tres tipos, medición de baja resistencia, medición de resistencia media y medición de alta resistencia. Si la medición de resistencia es posiblemente de unos pocos miliohmios a micro ohmios, entonces se considera una medición de baja resistencia.

Esta medición se utiliza realmente con fines de investigación. Si la medición es de 1 ohm a 100 k, generalmente se denomina medición de resistencia media. Potenciómetro, termistores, etc. la medición entra en esta categoría.

Y la medición de resistencia muy alta se considera de 100 kilo ohmios a más de 100 mega ohmios. Para encontrar el valor medio de la resistencia se utilizan diferentes métodos, pero sobre todo se utiliza el puente de Wheatstone.

¿Qué es Wheatstone Bridge?

La red de puentes más común y sencilla para encontrar la resistencia es el puente de Wheatstone de CC. Este puente se utiliza cuando se deben medir pequeños cambios en la resistencia, como en aplicaciones de sensores. Esto se usa para convertir un cambio de resistencia en un cambio de voltaje de un transductor.

La combinación de este puente con un amplificador operacional se utiliza ampliamente en industrias para varios transductores y sensores. Un puente de Wheatstone consta de cuatro resistencias que están conectadas en forma de diamante con la fuente de alimentación y los instrumentos indicadores, como se muestra en la figura.

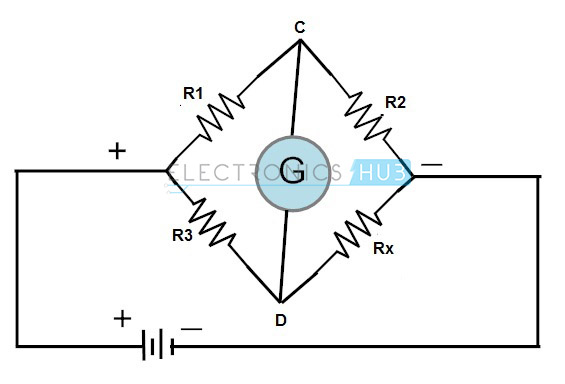
Este puente se utiliza para encontrar la resistencia desconocida de forma muy precisa comparándola con un valor conocido de resistencias. En este puente se utiliza la condición nula o equilibrada para encontrar la resistencia.

Para este puente, la tensión de condición equilibrada en los puntos C y D debe ser igual. Por lo tanto, no fluye corriente a través del galvanómetro. Para obtener la condición equilibrada, una de las resistencias debe ser variable.

From the figure,

The voltage at point D = V × RX / (R3 + RX)

The voltage at point C = V × R2 / (R1 + R2)

The voltage (V) across galvanometer or between C and D is,

VCD = V × RX / (R3 + RX) − V R2 / (R1 + R2)

When the bridge is balanced VCD = 0,

So,

V × RX / (R3 + RX) = V R2 / (R1 + R2)

RXR1 + RXR2 = R2R3 + R2RX

R1RX= R2R3

R2/R1= RX/R3

This es la condición para equilibrar el puente. Y para encontrar el valor desconocido de resistencia

RX = R3 × (R2 / R1)

De la ecuación anterior, R4 o Rx se pueden calcular a partir del valor conocido de resistencia R3 y la relación de R2/R1. Por lo tanto, la mayoría de los casos los valores R2 y R1 son fijos y el valor R3 es variable, de modo que se logra un valor nulo y el puente se equilibra.

Principio de funcionamiento

Sin el galvanómetro, el circuito del puente se parece a un circuito divisor de voltaje, como se muestra en la figura a continuación. Considere R1 = 20 ohmios, R2 = 40 ohmios para un brazo y para el otro considere los mismos valores de R3 y R4 respectivamente.

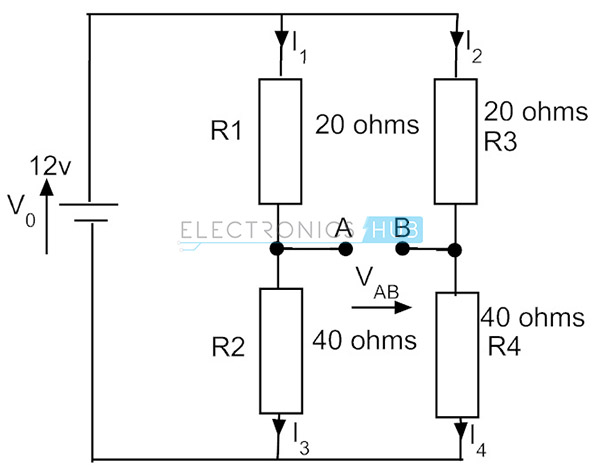
El flujo de corriente en el primer brazo es

I1 = V/ (R1+R2)

I1 = 12V/ (20+40)

I1 = 0.2 A

Y el voltaje en el punto C es igual a la caída de voltaje en la resistencia R2,

VR2 = I1 × R2= 0.2 × 40 = 8V

De manera similar, el voltaje a través de R1 es de 4V (0.2 × 20). Debido a los mismos valores de resistencia, las tensiones en R4 y R3 serán las mismas que las de R1 y R2 respectivamente. Por lo tanto, en los puntos A y B, los voltajes son los mismos, por lo que el galvanómetro muestra una lectura de cero, ya que la diferencia de potencial es cero. En este caso, se dice que el puente está en estado equilibrado.

Supongamos que si invertimos las resistencias en el segundo brazo, el flujo de corriente es el mismo debido al circuito en serie. Pero el voltaje a través de la resistencia R4 cambia, es decir, 0.2 * 20 = 4V. Así que en esta condición el voltaje a través de los puntos A y B es diferente y existe una diferencia de potencial de 8 – 4 = 4V. Esta es la condición desequilibrada del puente.

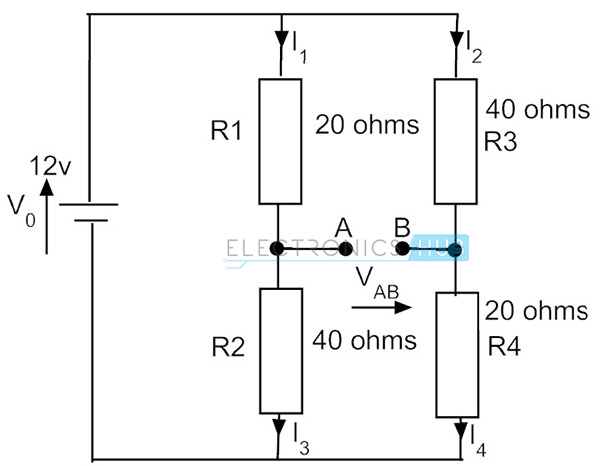
Ejemplo de puente de Wheatstone

Desde arriba, el puente de Wheatstone está desequilibrado cuando la lectura del voltímetro no es cero. Esta lectura puede ser positiva o negativa, dependiendo de las magnitudes de los voltajes en los terminales del medidor. Consideremos el siguiente circuito del puente de Wheatstone que está conectado para encontrar el valor de resistencia desconocido con el uso de la caja de década de resistencia para obtener la resistencia variable de R3.

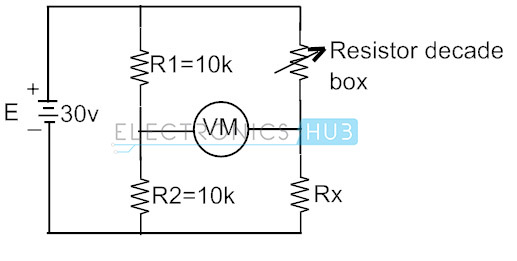
sabemos que la condición para el balance del puente es

R4 = R3 × R2 / R1

Rx = RBOX × (10 x 103)/ (10 x 103)

Rx = RBOX

Aquí, en este caso, el puente de Wheatstone es equilibrado por el ajuste de la década de resistencia de la caja hasta que el voltímetro lee el valor cero. Y el valor de resistencia correspondiente en la caja es igual a la resistencia desconocida. Supongamos que si la condición nula de voltaje ocurre a 250 ohmios de la caja de década de resistencia, entonces la resistencia desconocida también es de 250 ohmios.

Puente de Wheatstone para medición de deformación

Más comúnmente para medir la deformación, se utilizan galgas extensométricas cuya resistencia eléctrica varía con la deformación proporcional en el dispositivo. En la práctica, el rango de resistencia de las galgas extensométricas es de 30 ohmios a 3000 ohmios. Para una deformación dada, el cambio de resistencia puede ser solo una fracción del rango completo. Por lo tanto, para medir extremadamente una fracción de los cambios de resistencia con alta precisión, se utiliza la configuración de puente de Wheatstone. La siguiente figura muestra el puente de Wheatstone donde la resistencia desconocida se reemplaza con una galga extensométrica.

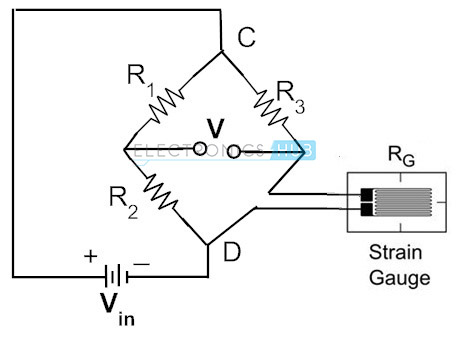
En el circuito anterior, dos resistencias R1 y R2 son iguales entre sí y R3 es la resistencia variable. Sin aplicar fuerza a la galga extensométrica, el reóstato se varía y finalmente se coloca de tal manera que el voltímetro indique una desviación cero. Esto se denomina condición de equilibrio de puente. Esta condición representa que no hay tensión en el medidor.

Si la galga extensométrica está tensa o comprimida, la resistencia puede aumentar o disminuir. Por lo tanto, esto causa un desequilibrio del puente. Esto produce una indicación de voltaje en el voltímetro que corresponde al cambio de tensión. Si la tensión aplicada en una galga extensométrica es mayor, entonces la diferencia de voltaje a través de los terminales del medidor es mayor. Si la tensión es cero, el puente equilibra y el medidor muestra una lectura cero.

Se trata de la medición de resistencia mediante un puente de Wheatstone para una medición precisa. Debido a la medición fraccionada de la resistencia, los puentes de Wheatstone se utilizan principalmente en mediciones de galgas extensométricas y termómetros.

Aplicaciones

1. El puente Wheatstone se utiliza para medir con precisión los valores de resistencia muy bajos.
2. El puente de Wheatstone junto con el amplificador operativo se utiliza para medir los parámetros físicos como temperatura, tensión, luz, etc.
3. También podemos medir las cantidades de capacitancia, inductancia e impedancia utilizando las variaciones en el puente Wheatstone.