The Four Colour Theorem
The Four Colour Conjecture was first stated just over 150 yearsago, and finally proved conclusively in 1976. Trata-se de um exemplo notável de como as velhas ideias combinam-se com novas descobertas e técnicas em diferentes domínios da matemática para proporcionar novas abordagens a um problema. É também um exemplo de como um problema aparentemente simples foi pensado para ser’ resolvido’, mas então tornou-se mais complexo, e é o primeiro exemplo espetacular onde um computador foi envolvido em provar um teorema matemático.
No Começo
A conjectura de que qualquer mapa pode becoloured usando apenas quatro cores apareceu pela primeira vez em uma carta fromAugustus De Morgan (1806-1871), primeiro professor de matemática sentado novo University College de Londres, para o seu amigo William RowanHamilton (1805-1865) o Irlandês famoso matemático, em 1852. Foi sugerido a Morgan por um de seus alunos, FrederikGuthrie, em nome de seu irmão mais velho Francis (que mais tarde tornou-se professor de matemática na Universidade da Cidade Do Cabo).


Augustus De Morgan (1807-1871) andWilliam Rowan Hamilton (1805-1865)
O problema, então, simplesmente de descrever, mas tão tentadoramente difficultto provar, capturado a imaginação de muitos matemáticos em thetime. No final da década de 1860 de Morgan até levou o problema e sua prova para a América, onde, entre outros, Benjamin Peirce (1809-1880), um matemático e astrônomo famoso, tornou-se interessado nele como distante para desenvolver seus métodos lógicos.de Morgan usou o fato de que em um mapa com quatro regiões, cada uma das outras três, uma delas está completamente fechada pelos outros. Como ele não conseguiu encontrar uma maneira de provar isso, ele usou-o como um axioma , a base de sua prova.
a copy of de Morgan’s originalsketch in his letter to Hamilton and a simple four colour map.em 1878, Arthur Cayley (1821-1895), em uma reunião da sociedade anatômica de Londres, perguntou se alguém tinha encontrado uma solução para a pergunta original de Morgan, mas embora tivesse havido algum interesse, ninguém tinha feito qualquer progresso significativo. Cayley becameinterested no problema e em 1879 publicou um pequeno paperOn a coloração da mapswhere ele explicou algumas das dificuldades na tentativa de proofand fez algumas contribuições importantes para a forma como o problema wasapproached. A sua pergunta é a seguinte: “se um determinado mapa já tiver sido bem sucedido, com quatro cores,e se acrescentarmos outra área, podemos manter a mesma cor?”iniciou-se uma outra linha de investigação que levou à aplicação deindução matemática ao problema.

Arthur Cayley (1821-1895)
Arthur Cayley mostrou que, se fourcolours já tinha sido usada para colorir um mapa, e uma nova região wasadded, nem sempre foi possível manter o originalcolouring.
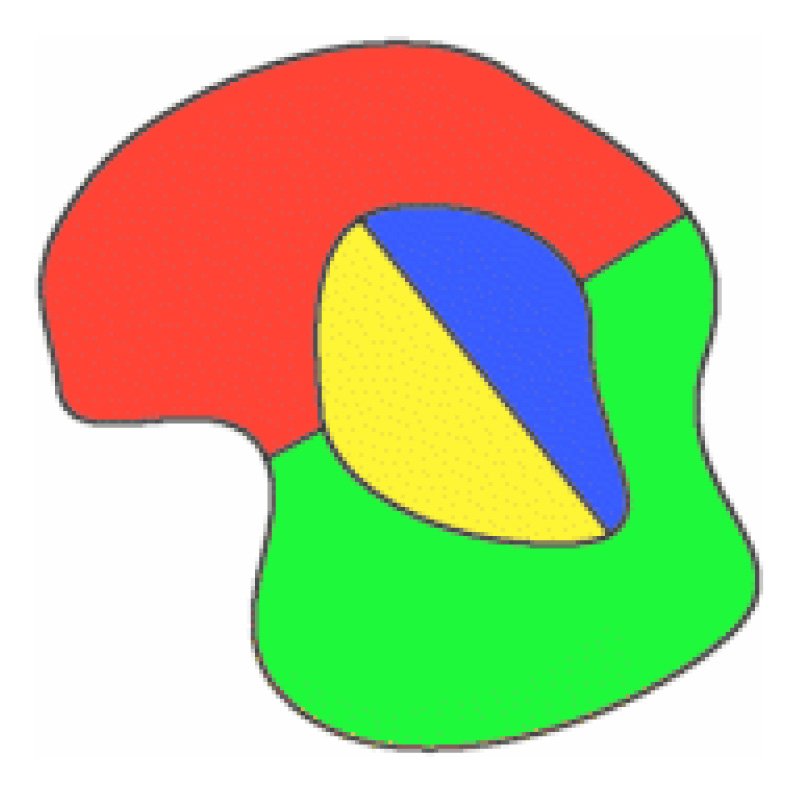
acima, todas as quatro cores foram usadas no mapa original, e uma nova região é desenhada para rodeá-lo. Neste caso, uma região vermelha mudou para azul, de modo que o vermelho pode ser usado na nova região circundante.
Cayley also observed that it was possible to solve a version of the problem by restricting the way the boundaries met. Por exemplo, os mapas onde apenas três países se encontraram têm três bordas se reunindo em avertex. Estes são chamados de “mapas cúbicos”, e os mapas utilizados na discussão seguinte são todos mapas cúbicos. Além disso, se um mapa puder ser colorido com quatro cores, apenas três cores aparecerão na fronteira.
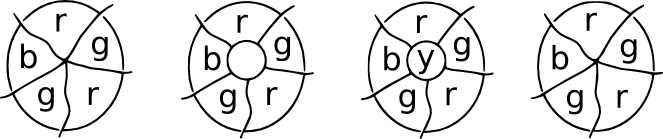
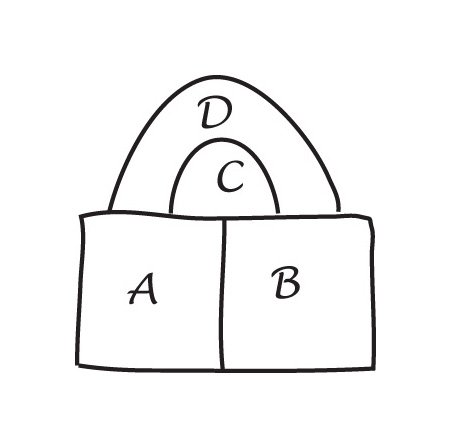
O Patch de demonstração. Imagine que em algum lugar de um mapa vários países se encontram em um ponto. Agora coloque um patch sobre o ponto de encontro, e todos os novos pontos de encontro terão Três Fronteiras emanando deles. Estes são mapas cúbicos, e uma quarta cor pode ser usada para a região central. Ao remover o adesivo, podemos voltar à coloração original.
algumas técnicas antigas, novas condições e mais problemas!
a fim de acompanhar os desenvolvimentos do problema, precisamos investigar brevemente algumas das ideias, procedimentos e tecnologias que os matemáticos desenvolveram nas suas tentativas de resolvê-lo.
a única conjectura de cinco vizinhos
‘Se não conseguir resolver um problema aparticular, encontre um mais fácil que possa resolver.'(Polya. Como resolvê-lo)
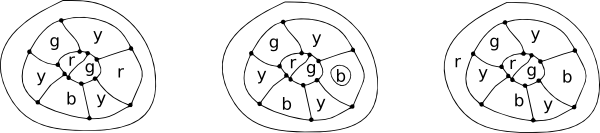
‘cada mapa tem pelo menos um país com cinco ou menos vizinhos.Imagine um mapa de uma ilha rodeada pelo mar. No povoamento dos países da ilha, o mar é considerado uma região única. Alguns países podem ter apenas duas fronteiras (um digon), algumas três (como em um triângulo), algumas quatro (um quadrado) e algumas cinco (aptógono) ou mais.
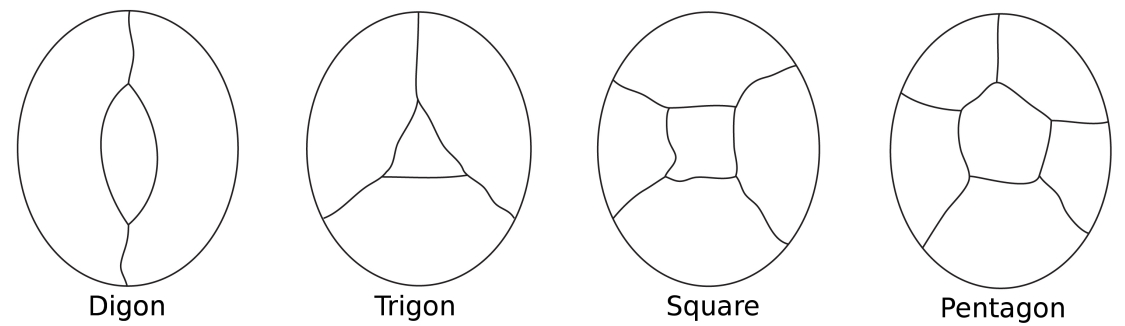
as possíveis configurações mais simples para circundar uma região central.
Note que em todas estas configurações cada nó tem apenas trechos.
em 1813, a fórmula de Euler para poliedra foi adaptada para duas dimensões por Augustin Cauchy (1759-1857) ao empurrar o poliedro para um plano formando assim a rede de thesolid. Desta forma, a fórmula tornou – se $f + v-e = 1$, porque Cauchy não contou a região “externa” da rede.

Augustin Cauchy (1759-1857)
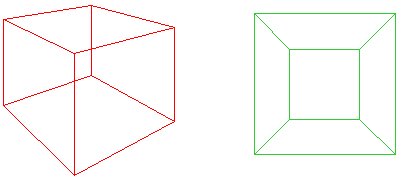
Imagine esmagar o cubo vermelho downonto um plano de modo que sua base está aberto para formar o outsideedge da rede verde. A ideia de Cauchy era cortar uma face do lubrificante, de modo que para um polígono de avião, $f + v – e = 1$. Alternativamente, se o ‘fora’ da rede é considerado como uma face com infinitearea, então ainda temos $f + v-e = 2$
podemos assumir que existem pelo menos três linhas de fronteira (arestas)emergindo de cada ponto de encontro (vértices).
A prova de que o mapa tem pelo menos um país rodeado por cinco ou menos vizinhos prossegue por contradição. Se isso levar a um absurdo, temos uma prova.
Agora coloque estes valores na fórmula de Euler: $$F + v-e = 2$$ e temos $1/3 (e) + 2/3(e) – e$$ $ que é zero!este é o absurdo, por isso a nossa suposição original era falsa.Isto significa que deve haver pelo menos um país com cinco ou menos vizinhos!criminosos mínimos!
outra forma de resolver o problema das quatro cores é assumir que é FALSE, e ver onde isso leva. Suponha que existem mapas que precisam de cinco cores ou mais, e nós escolhemos os mapas com o menor número possível de Países. Estes mapas são chamados de contra-exemplos mínimos ou criminosos iminimais !isto significa que um criminoso mínimo não pode ser colorido com quatro cores,mas qualquer mapa com menos países pode ser colorido com quatro cores. Se pudermos mostrar que criminosos mínimos não podem existir, então poderemos fazer alguns progressos.
Por exemplo, podemos mostrar que um criminoso mínimo não pode conter um digon.
do mapa original, retire um limite do digon, e teremos um novo mapa com menos Países. Este mapa pode ser colorido com quatro cores (a partir da nossa suposição). Em seguida, colorimos este newmap (só precisamos de duas cores). Agora substitua a fronteira que removemos, e volte a pintar o mapa. Temos usado três cores, e uma vez que ainda há mais uma cor disponível, isto mostra que o nosso mapa pode ser colorido com quatro cores. Mas isto é contra a nossa suposição, por isso um criminoso mínimo não pode deter um digon.
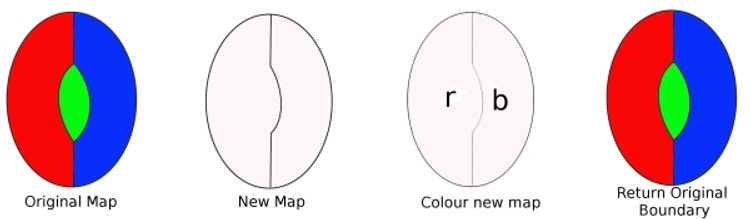
Para mostrar que um Mínimo de Criminalcannot conter uma região com duas bordas (a digon). Suponha que há um criminoso mínimo que contém um digon. A remoção de uma aresta significa que o mapa contém menos regiões. Este novo mapa pode ser colorido com quatro cores. Agora substitua a borda perdida. Uma vez que só eram necessárias duas colorações antes, substituir a aresta significa que podemos usar a cor de um terço, e ainda ter uma quarta cor para usar. Assim, um criminoso mínimo pode ser colorido com quatro cores. Por isso, um criminoso minimalnão pode conter um digon.
este procedimento pode ser repetido para mostrar que um crime mínimo não pode conter um país de três lados (um trigon), mas se quebra quando tentamos a técnica em um quadrado, porque Quando substituímos o tabuleiro, os países ao lado dele podem muito bem estar usando todas as quatro cores, de modo que o procedimento de prova falha. Uma vez que isso aconteceu, torna-se óbvio que não funcionará para pentágonos, e assim por diante.
o teorema das Seis cores
uma técnica similar pode ser aplicada para mostrar que o “Six colourtheorem” é verdadeiro. Primeiro, assumimos que não há mapas que possam ser coloridos com seis cores. Alguns dos mapas podem ser coloridos com sete cores, por isso, ao seleccionar um destes (um criminoso mínimo), se pudermos mostrar que é possível colori-lo com menos de sete cores, atingimos o nosso objectivo.
a partir da prova do teorema dos cinco vizinhos, é possível utilizar a ideia criminosa mínima para mostrar que qualquer mapa pode ser colorido com seis cores!
de regiões A Nós, redes e Topologia
Em 1879 Alfred Kempe (1849-1922), usando técnicas semelhantes às descritas acima, começou a partir da “propriedade de cinco vizinhos” e desenvolveu um procedimento conhecido como o método de “cadeias Kempe” para encontrar uma prova do teorema das quatro cores. Publicou esta prova no American Journal of Mathematics. Ele encontrou dois mais simples versionsthat foram publicados no ano seguinte, e sua prova ficou para tenyears antes de Percy Heawood (1861-1955) mostraram não haver animportant erro na prova-método que Kempe tinha usado.


Alfred Kempe (1849-1922), PeterGuthrie Tait (1831-1901) e Percy Heawood (1861-1955)
Em 1880, P. G. Tait (1831-1901), um físico matemático, offereda solução para o problema. Independentemente, Tait tinha estabelecido que os mapas onde um número par de linhas de fronteira se encontram em cada ponto,poderiam ser coloridos com duas cores, embora este resultado tivesse aparecido mais cedo nos trabalhos de Kempe.
durante 1876-77 Tait tornou-se bem conhecido por seu estudo e classificação de nós. Naquela época havia uma série de teorias diferentes sobre a estrutura dos átomos. William Thompson (later, Lord Kelvin 1824-1907) inspired by the experiments of Thegerman Physicist Hermann von Helmholtz (1821-1894) proposed ateory that atoms were knotted tubes of ether. A teoria de Kelvin de “átomos de vórtice” foi levada a sério por cerca de vinte anos, e levou Tait a realizar uma classificação de nós. Tait, Thomsonand James Clark Maxwell (1831-1879) inventaram muitas ideologias topológicas durante os seus estudos. No entanto, a teoria de Kelvin foi fundamentalmistaken e os físicos perderam o interesse no trabalho de Tait.


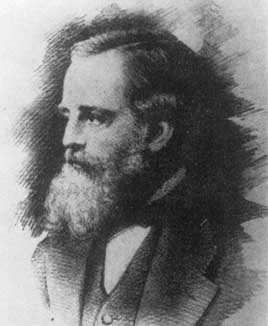
Hermann von Helmholtz (1821-1879),Lord Kelvin (1824-1907) e James Clark Maxwell (1831-1879)

Tait começou com as formas em que um único circuito fechado de cabo poderia ser atado. Ele não tinha nenhum método sistemático no início, e começou de uma forma intuitiva, tomando um único ciclo fechado e experimentando as formas em que ele poderia ser tricotado. É claro que a corda tinha que ser aberta (como ashoelace), em seguida, tricotada, e unida. Note que, se você seguir o acorde em torno do nó, as passagens’ sobre-sob ‘ alternarão.Ele então passou a experimentar com dois loops e as maneiras em que eles poderiam ser unidos juntos. Mostrados aqui são nós com até 6crossings para um único laço.
um dos resultados do estudo de Tait foi sua conjectura de grafo Hamiltoniano.
um mapa é considerado como um poliedro desenhado sobre uma esfera, e Cantão é projetado em um plano. Tait propôs que qualquer mapa cubicpolyhedral tem um ciclo Hamiltoniancycle . O método de Tait focado nas arestas do grafo andhe mostrou que um ciclo Hamiltoniano poderia produzir uma Quatro-coloração de um mapa. Foi apenas em 1946 que William Tutte (1917-2002) encontrou o primeiro contra-exemplo para a conjectura de Tait.
Tait and the connection with knots
Tait initiated the study of snarks in 1880, when he proved that the fourcolour theorem was equivalent to the statement that no snark isplanar. Um grafo planar é aquele que pode ser desenhado no plano sem arestas atravessando. It looks as if Tait’s idea of non-planar graphsmight have come from his study of knots and Hamiltonian paths .
O primeiro snark foi o grafo de Petersen descoberto em 1898,e os matemáticos começaram a caçar mais de um desses tipos de graphsbut não foi até 1946 que outro snark foi encontrado.
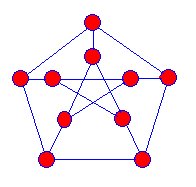 |
Snarks são projeções tridimensionais, gráficos para theplane. Não há vértices onde as arestas azuis parecem cruzar-se. Snarks têm as seguintes propriedades:
|
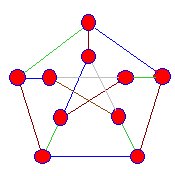 |
As bordas da reunião os vértices deste snark são de cor azul,verde e marrom, mas estamos sempre a chegar a uma fase onde este processcannot ser continuado. |
Júlio Peterson (1839-1910)
A Caça de theSnark é um poema escrito por Lewis Carroll, e Martin Gardnernamed estes gráficos Snarks, porque eles estavam tão indescritível.
transformar o problema e encontrar novos métodos.
embora Hewood tenha encontrado a maior falha no método de prova de Kempe em 1890, ele foi incapaz de continuar a provar o teorema das quatro cores, mas ele fez um avanço significativo e provou conclusivamente que todos os mapas poderiam ser coloridos com cinco cores.
Hewood fez muitas contribuições importantes para o problema,mudando o foco de atenção das áreas de um mapa, para as fronteiras entre eles. Em 1898, ele tinha provado que se o número de pediges em torno de cada região fosse divisível por 3, então as regiões poderiam ser coloridas com quatro cores.a prova de Cauchy da fórmula de Euler também incluiu a ideia de que qualquer rede de um poliedro pode ser triangulada adicionando arestas a faces de makenon-triangulares em triângulos. Em seguida, desenvolveu um procedimento onde apagou as arestas uma a uma, mostrando que a fórmula de Euler poderia ser mantida em cada passo.
Cauchy’s Proof of Euler’s Formula
Cauchy’s 1813 proof of Euler’s Formula began with the idea of aprojection of a polyhedron to obtain a plane net. Ele ainda demonstrou (a) que qualquer rede poderia ser triangulada, e sua prova(B) da fórmula de Euler foi aceita na época.
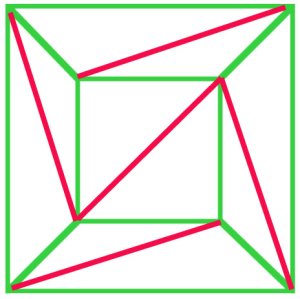 (a)
|
In principle, every polygonal net can be triangulated. In thisnet of a cube (a), $f + v – e$ is $10 + 8 – 17 = 1$, and Euler’sformula still holds. |
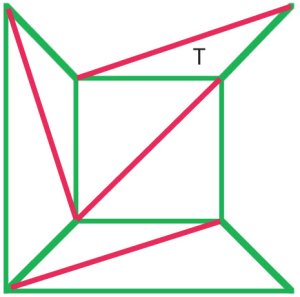 (b)
|
Cauchy argumento foi para remover as bordas externas a partir de diagramas de(a) um por um, e quando ele atingiu um estágio como no diagrama (b)removido todo o triângulo T, preservando, assim, fórmula de Euler. Manymathematicians of the early nineteenth century agreed that this processure demonstrated a proof of Euler’s formula for allpolyhedra. |
por 1900, matemáticos sabiam que um grafo planar pode ser estruturado a partir de qualquer mapa usando o conceito poderoso da dualidade . No dual, as regiões são representadas por vértices e dois vértices são unidos a aresta Biana se as regiões são adjacentes. Nestes grafos, a conjectura de Quatro cores agora pergunta se os vértices do grafo podem ser coloridos com 4 cores, de modo que nenhum dois vértices adjacentes são a mesma cor.
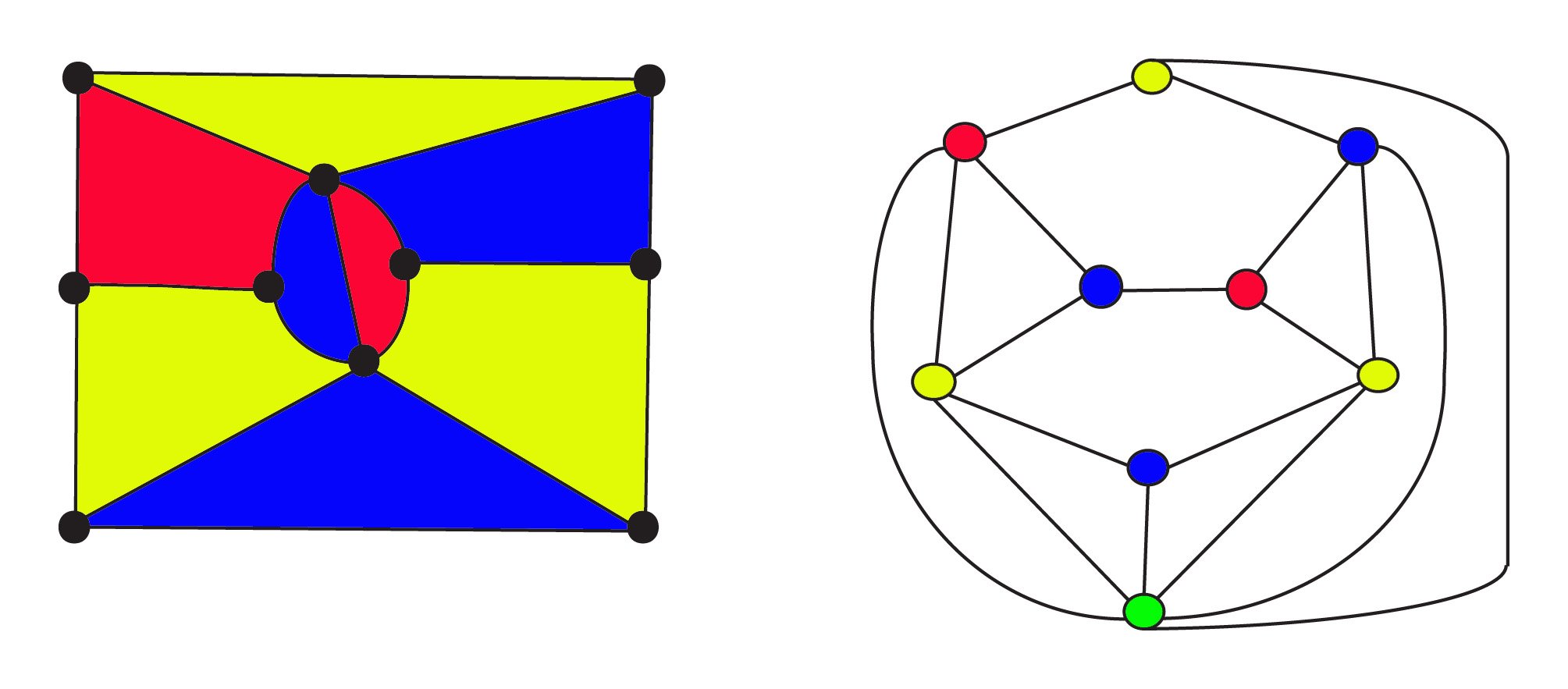
O 3-cor do mapa à esquerda tem$8$ regiões de us $10$ vértices e us $17$ bordas. Seu grafo duplo à direita tem$ 9 $ regiões $ 9$ vértices e$ 17 $ arestas onde os vértices são coloridos da mesma forma que as áreas do mapa. O greenvertex na parte inferior do grafo representa a área externa infinita para o mapa. Tanto o mapa original como a sua formula dual obedecem a Euler para as redes $f + v – e = 1$ ou, $\text{regions} +\text{vertices} – \text{edges} = 1$. A relação da dualidade issimétrica: o dual do dual será o grafo original, onde as regiões e vértices são trocados.
Durante a primeira metade do século xx, mathematiciansfocused sobre como modificar estes tipos de técnicas para reducecomplicated mapas para casos especiais, que poderia ser identificada andclassified, para investigar as suas propriedades particulares anddeveloped a idéia de um conjunto mínimo de mapa configurações thatcould ser testado.
Na primeira instância, o conjunto foi pensado para conter nearly9,000 membros, o qual foi uma tarefa enorme, e por isso o mathematiciansturned para técnicas de computador para escrever algoritmos que poderia fazer thetesting para eles. The algorithms used modified versions of Kempe’s origin idea of chains together with other techniques to reduce the number of members of the minimal set.depois de colaborar com John Koch sobre o problema da redução, em 1976 na Universidade de Illinois, Kenneth Appeland Wolfgang Haken eventualmente reduziu o problema dos testes para um conjunto inevitável com 1.936 configurações, e uma solução completa para a conjectura de Quatro cores foi alcançada. Este problema de verificar a reducibilidade dos mapas, um por um, foi duplamente verificado com diferentes programas e diferentes computadores. A sua prova demonstrava que pelo menos um mapa com o menor número possível de regiões que exigem cinco cores não pode existir.
desde a primeira prova, algoritmos mais eficientes foram encontrados para mapas de 4 cores e, em 1994, o conjunto inevitável de Configurações foi reduzido para 633.
é uma “prova” feita em um computador uma prova adequada?como a prova foi feita com a ajuda de um computador, houve um clamor imediato. Muitos matemáticos e filósofos afirmaram que a prova não era legítima. Alguns diziam que as provas deveriam ser “provadas” por pessoas, não por máquinas, enquanto outros, de uma mente mais prática questionavam a confiabilidade dos algoritmos e a capacidade das máquinas para realizá-las sem erro.No entanto, muitas das provas escritas por matemáticos têm sido consideradas defeituosas, então o argumento sobre confiabilidade parece vazio.Independentemente das opiniões expressas, a situação conduziu a um debate sério sobre a natureza da prova, que ainda hoje continua.
para notas pedagógicas:
Use a página notas no topo deste artigo ou clique aqui.
Notes
- More detail of this and the other procedures found in thissection can be seen in Robin Wilson’s book Four Colours Sufferent .os nós podem ser canhotos ou destros, e hoje existem importantes aplicações desta propriedade em química, farmácia,biologia e física. (Veja notas pedagógicas)
- nomeado em homenagem a William Rowan Hamilton (1805-1865). Um caminho Hamiltoniano em um grafo visitseach vértice exatamente uma vez. Um ciclo Hamiltoniano (ou circuito) é um apath que visita cada vértice exatamente uma vez e retorna ao vértice iniciante.(See Pedagógic Notes)
- O Livro de Imre Lakatos, Proofs and Refutations has adiscussion and criticism of Cauchy’s procedure (pages 6 – 12), andmuch more on the story of Euler’s Theorem.a ideia da dualidade surgiu nos séculos XVI e XVII com desenvolvimentos em geometria projetiva. Matemáticos como Pascal andDesargues descobriram que novos teoremas podiam ser encontrados trocando os Termos “ponto” e “linha” em descrições de certas configurações geométricas. Um exemplo é em poliedros regulares, onde os vértices de um correspondem às faces do outro. Assim, o dual de um tetraedro é outro tetraedro,e o dual de um cubo é um octaedro. O dual do dual é o polígono de origem.
the very best popular, easy to read book on the Four ColourTheorem is:
Wilson, R. (2003)
Four Colours Sufferent.
London. Penguin Books.
For a more detailed and technical history, the standardreference book is:
Biggs, N.; Lloyd, E. & Wilson, R. (1986) (1998)
Graph Theory,1736-1936
Oxford. Oxford University Press.este traz-nos à actualidade, com fundações e filosofia mais recentes.
Fritsch, R and Fritsch, G (2000)
The Four Color Theorem: History,Topological Foundations, and Idea of Proof
New York. Springer-Verlag.
quase nenhum livro de história geral tem muito sobre o assunto, mas o último capítulo em Katz chamado “computadores e aplicações” tem assecção na teoria dos grafos, e o teorema das quatro cores é mencionado duas vezes.Polya G. Como resolver.este é o livro clássico sobre resolução de problemas. Tem havido muitas edições deste livro desde que ele apareceu pela primeira vez na década de 1950 e ainda está facilmente disponível. Curiosamente, edições recentes deram origem ao subtítulo “um novo aspecto do método matemático”.
Lakatos, I. (1976) Proof andRefutations: the Logic of Mathematical Discovery.
Cambridge. C. U. P.
Este é outro livro importante que levou à pesquisa de resolução de problemas e investigações na década de 1970. Começa como uma discussão em sala de aula entre um professor e um grupo de estudantesobre a prova da fórmula de Euler, e varia através das ideias,objeções e possibilidades que foram realmente discutidas porimatematicianos e cientistas no século XIX. É uma das questões mais importantes sobre a resolução de problemas de ensino e aprendizagem e sobre os métodos matemáticos e a prova.
references Related
i have had a little book on String Games for some time. Quando eu estava na escola chamava-se Cat’s Cradle, e tocámo-lo na nossa época de alvorada.recentemente, uma revista francesa publicou um artigo sobre o’ Algebra ‘ de figuras de cordas! Se você for para a Amazon, você encontrará um livro de Anice de Ann Swain e Michael Taylor chamado Finger Strings: um livro de Cats berços e figuras de cordas a ser publicado pela Floris books em Setembro de 2008. Existem cerca de 80 figuras descritas com cores diagrams.It a espiral vai ficar aberta enquanto segues as instruções. Ele também vem com um par de laços de corda!
para especialistas em nós, o AshleyBook dos nós é um clássico para qualquer pessoa interessada nos sonhos de diferentes tipos de nós e seus usos. A Amazon tem várias edições disponíveis a preços diferentes.
web Links
para uma visão geral e links para muitas pessoas e tópicos, o Website do usuário é
E, claro, biografias MacTutor de todos os envolvidos no desenvolvimento de todos os diferentes aspectos matemáticos podem ser encontrados no Índice de biografias do MacTutor.
O teorema das quatro cores e três provas. Para o matematicamente persistente, o seguinte website tem uma nova abordagem intrigante para atacar o problema de construir um novo algoritmo para resolver o problema, e tentar reduzir a dependência de um computador.http://www.emu.edu.tr/~cahit/the%20four%20color%20theorem%20—%20three%20proofs.htm
Para A Teoria dos Grafos, Wikipedia dá uma boa visão geral, e você pode esquiar o material realmente técnico. Ele mostra os tipos de aplicações modernas desta área da matemática. Se você for para GraphColouring e clicar no teorema das quatro cores, então você vai encontrar muito mais informações.
An interesting, and not too technical History of Knot Theory-how an idea from Kelvin’s Physics returns to Atomic Theorytoday.
A Associação de Professores de matemática tem cartazes de Knotdesign Celta. Vá ao seu site e navegue na lista alfabética de recursos.
descubra tudo Sobre nós no Atlas dos nós! Se você não é um perito – basta desfrutar da variedade e complexidade da base de dados “no espírito do wiki”
Mais artístico e colorido – mas não menos matemático é o local da trama conhecida.
For those who want some of the original stuff and historicaldetail go to the History of Knot Theory on: