símbolos do diagrama de Venn explicados
símbolos do diagrama de Venn
∪: união de dois conjuntos. Um diagrama Venn completo representa a união de dois conjuntos.
∩: intersecção de dois conjuntos. A intersecção mostra quais itens são compartilhados entre categorias.
Ac: complemento de um conjunto. O complemento é o que não está representado em um conjunto.está na hora de ter uma conversa séria sobre diagramas Venn—e não estamos a falar dos diagramas Venn dos seus dias de escola primária. Estamos a falar dos visuais hardcore produzidos por profissionais sérios para representar ideias matemáticas complexas.diagramas
Venn são representações visuais de conjuntos matemáticos—ou coleções de objetos—que são estudados usando um ramo da lógica chamado Teoria dos conjuntos. A teoria dos conjuntos é um dos sistemas fundamentais para a matemática, e ajudou a desenvolver a nossa compreensão moderna do infinito e dos números reais.pesquisadores e matemáticos desenvolveram uma linguagem e um sistema de notação em torno da teoria dos conjuntos. Se você quiser entrar em seus segredos, você vai querer se familiarizar com estes símbolos de diagrama de Venn.
Este guia irá guiá-lo através do processo de fazer um diagrama de Venn, explicando os símbolos ao longo do caminho. Estaremos usando Lucidchart para construir nossos exemplos porque é fácil de usar e completamente livre. Se você gostaria de acompanhar ou construir o seu próprio diagrama Venn, tudo que você tem a fazer é clicar em baixo e criar uma conta gratuita. Agora vamos a isso!
diagramas de Venn e teoria dos conjuntos
Existem mais de 30 símbolos usados na teoria dos conjuntos, mas apenas três que você precisa saber para entender o básico. Depois de dominares isto, estás à vontade para passar às coisas mais complicadas.
União de dois conjuntos: ∪
cada círculo ou elipse representa uma categoria. A união de dois conjuntos é representada por ∪. (Não confunda este símbolo com a letra “U.”)
Este é um diagrama de Venn de dois círculos. O círculo verde é A, e o círculo azul é B. O diagrama de Venn completo representa a união de A E B, ou a ∪ B. Sinta-se à vontade para clicar na imagem para tentar este diagrama como um modelo.
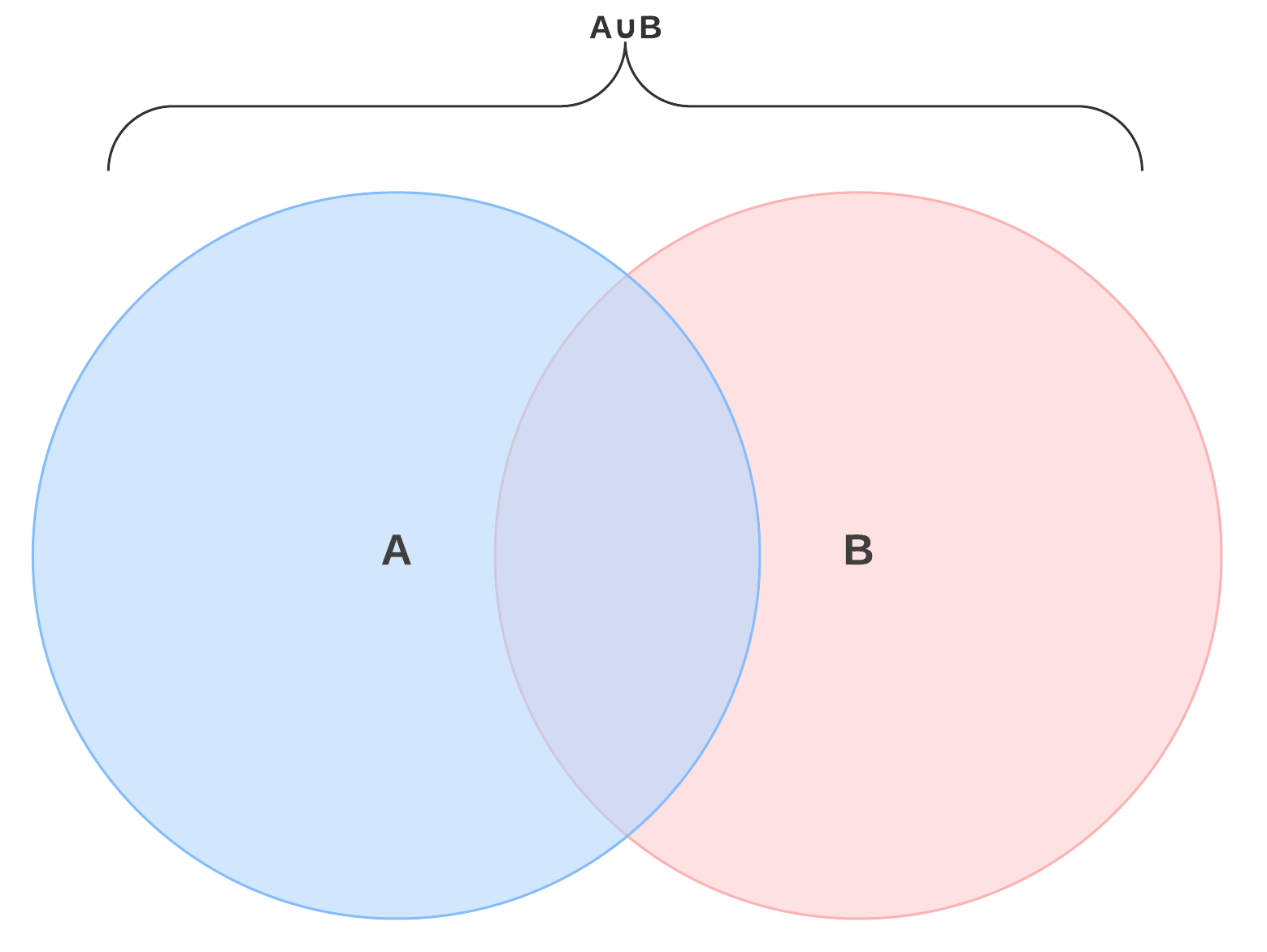
What would the union of two sets look like in the real world? Set a pode representar um grupo de pessoas que tocam piano. O Set B pode representar guitarristas. A ∪ B representa aqueles que tocam piano, guitarra ou ambos.
intersecção de dois conjuntos: ∩
ao fazer um diagrama de Venn, estamos muitas vezes interessados na intersecção de dois conjuntos—isto é, que itens são compartilhados entre categorias. Neste diagrama, a área marreca (onde o azul e o verde se sobrepõem) representa a intersecção de A E B, ou a ∩ B.
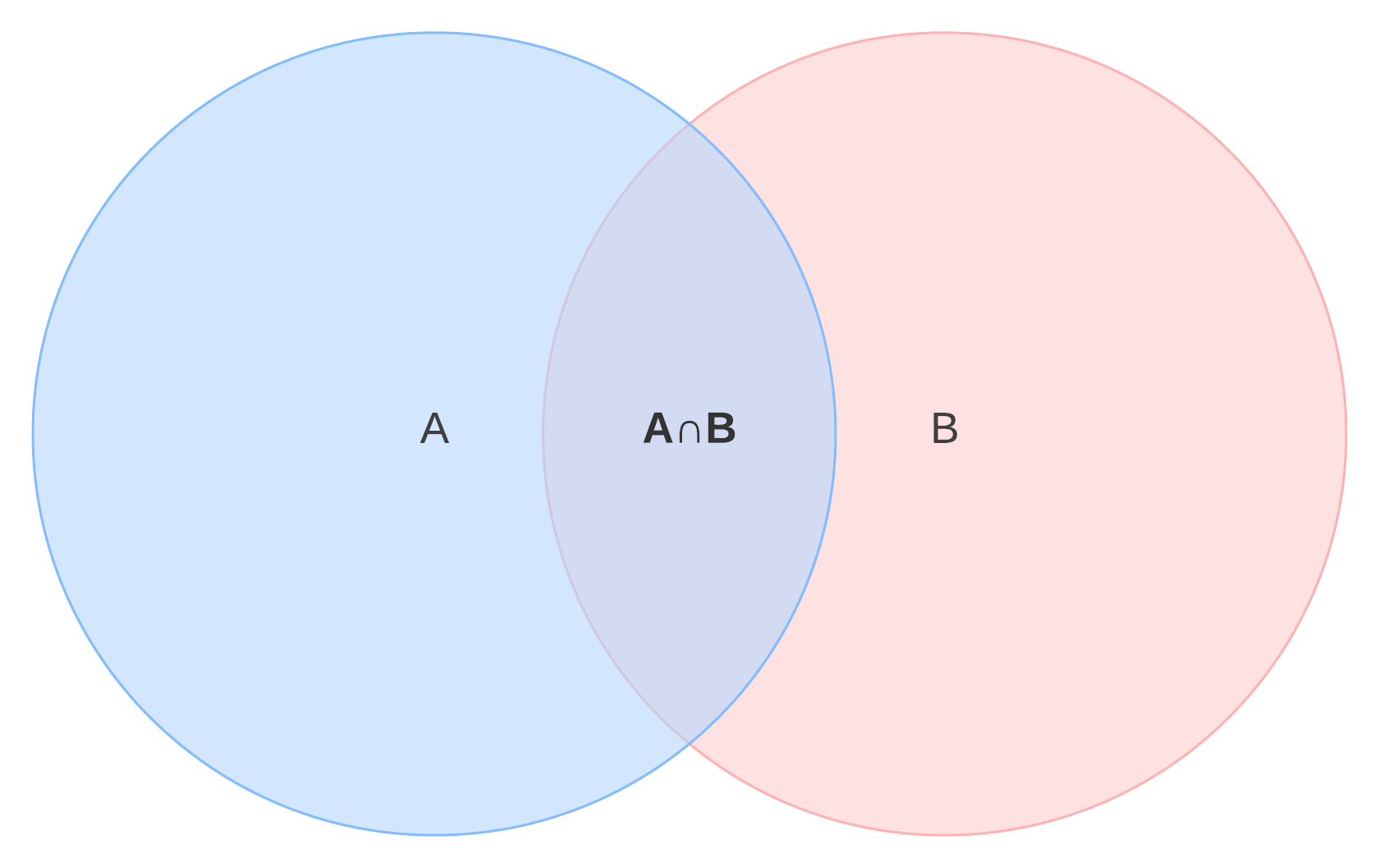
Para continuar o exemplo, o cruzamento de piano e guitarra jogadores inclui aqueles que dominam ambos os instrumentos.
complemento de um conjunto: Ac
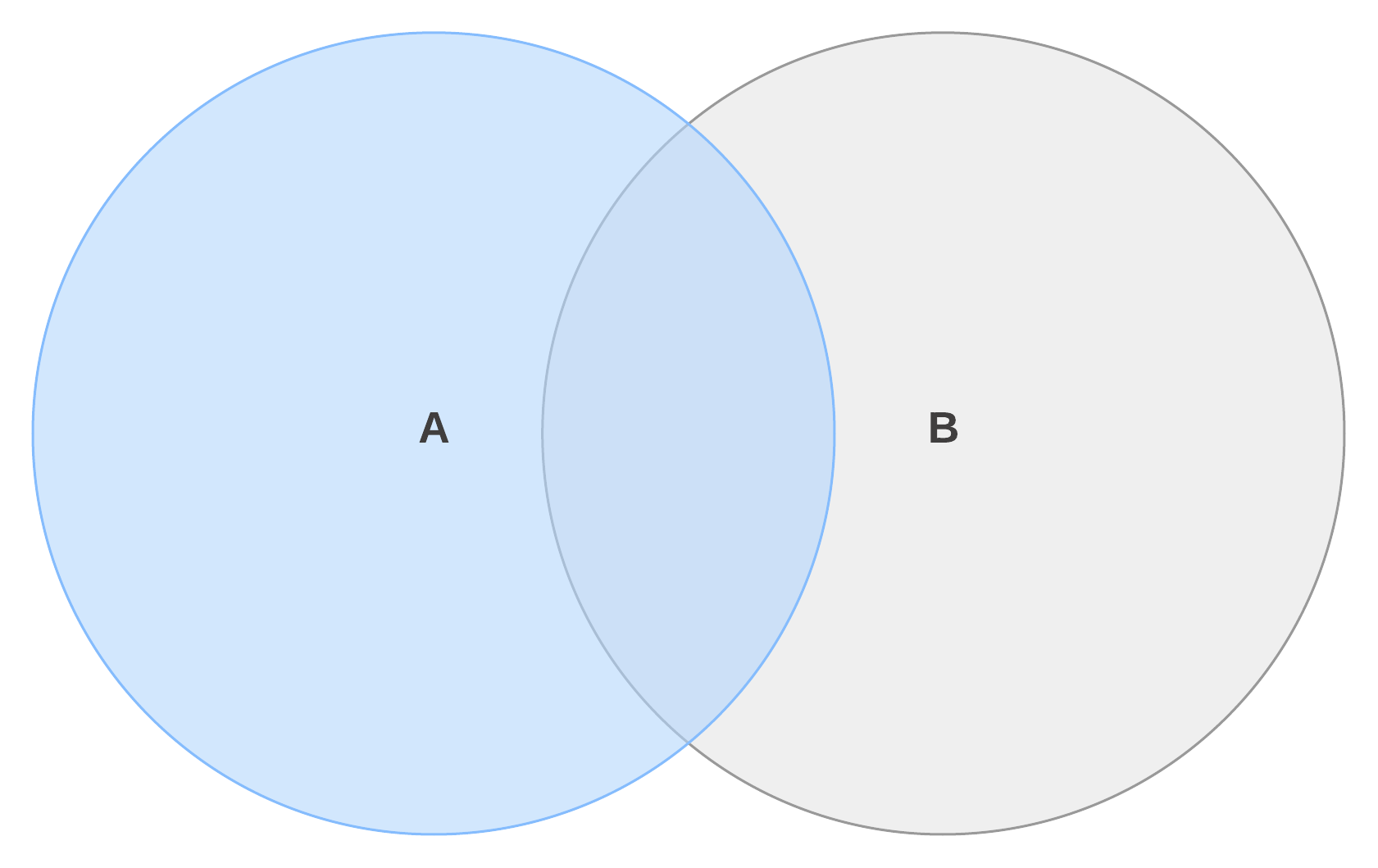
ao fazer um diagrama de Venn, você também pode querer considerar o que não é representado num conjunto. Este é o complemento de um conjunto, ou Ac, para o conjunto A.
O complemento absoluto de um conjunto é tudo o que não está incluído no conjunto. Isto significa que, dado um universo U, a letra desta vez), tudo o que existe no universo, exceto Uma, é a absoluta complementar de A em U. Isto pode ser representada pela equação Ac = U \ A.
A seguir está uma Cademeuuisque diagrama para o absoluto como complemento de Uma em U. O cinza seção mostra tudo fora de A. o instrumento musical caso, seria de todo aquele que não jogar o piano.
Um fast food diagrama de Venn ilustrando a teoria dos conjuntos
Para o ajudar a solidificar a aplicação prática da teoria dos conjuntos, vejamos através de um exemplo. Vamos começar com um levantamento das preferências de fast food de três pessoas. Estas três pessoas, a quem atribuiremos A, B E C, indicam que restaurantes gostam. Um diagrama de três círculos cobre todas as possibilidades: que um restaurante não será escolhido por nenhum entrevistado, um, dois ou todos os três.Aqui estão os resultados.:
| Restaurant | A | B | C |
|---|---|---|---|
| McDonald’s | X | X | |
| Wendy’s | X | X | |
| Burger King | |||
| In-N-Out | X | X | |
| Taco Bell | X | X | |
| KFC | |||
| A&W | |||
| Chick-fil-A | X | X | X |
Agora é hora de criar um diagrama de Venn representando os resultados. Começamos com este modelo abaixo. Ele usa o símbolo que explicamos,∩, para mostrar a intersecção entre dois e três conjuntos. Há oito regiões que os nossos restaurantes podem ocupar.
now we fill in our Venn diagram according to the results. No A B B, temos o Wendy’s porque o respondente a e o respondente B o escolheram. Burger King foi escolhido por ninguém, mas existe no universo de restaurantes de fast food disponíveis, então ele vai no espaço branco fora do diagrama. A intersecção de todos os Três, A ∩ B ∩ C, tem Chick-fil-A, uma vez que todos os três entrevistados o escolheram.
Aqui está o que o final do diagrama parece:
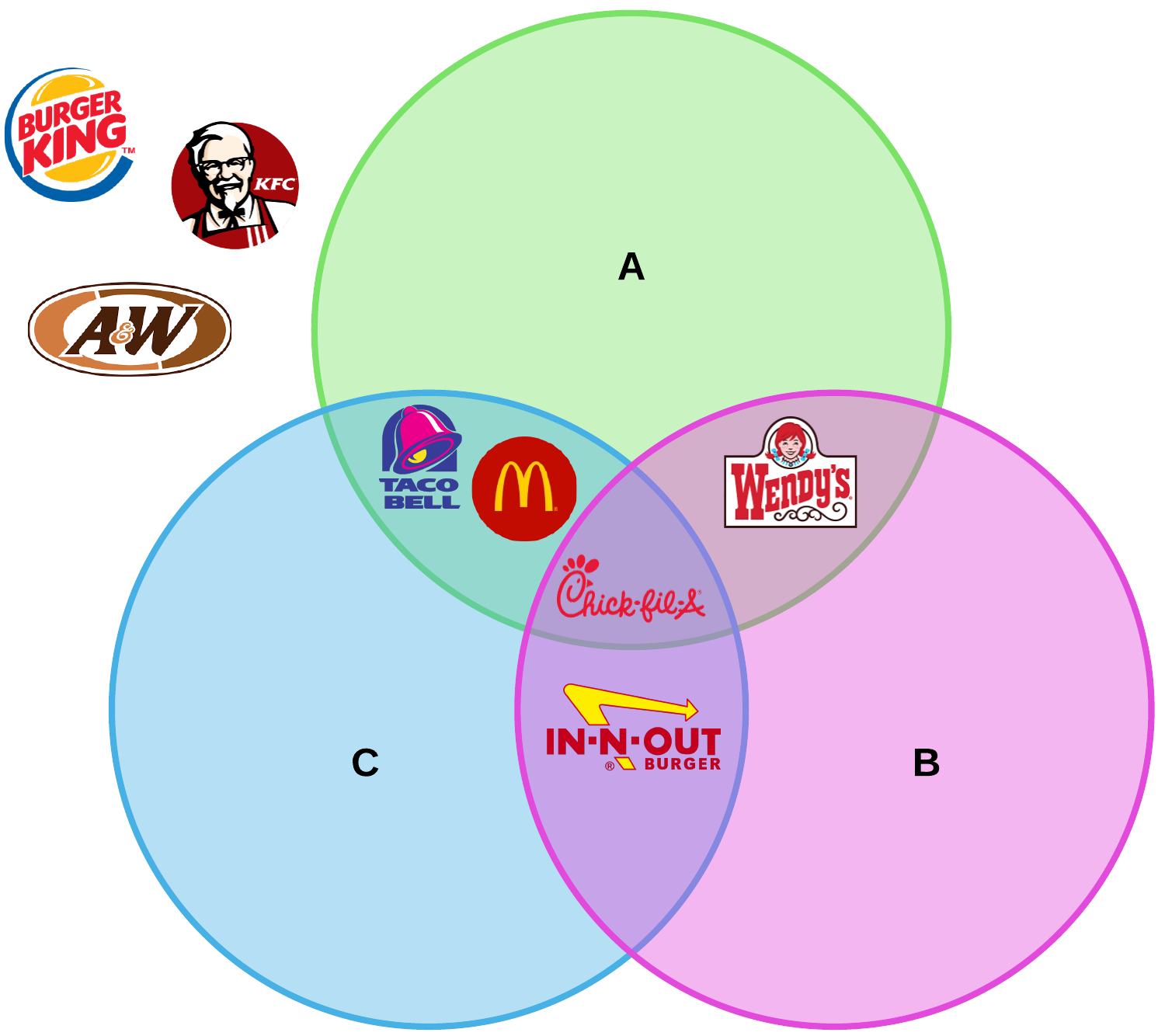
Agora temos um auxílio visual se estamos escolhendo onde estas três pessoas devem sair para o almoço!
Agora que você viu um diagrama de Venn em ação, aqui está um exemplo que você pode facilmente personalizar para criar o seu próprio!

Agora que você sabe o diagrama de Venn símbolos, leia como fazer um!
Aprenda como
leitura adicional para símbolos de diagramas de Venn
Se estiver interessado em aprender mais sobre a teoria dos conjuntos e criar diagramas de Venn de alta qualidade, Existem vários recursos disponíveis. Por exemplo, a enciclopédia Stanford tem uma introdução à teoria básica dos conjuntos.
para saber mais sobre a história dos diagramas de Venn, leia a resposta da nossa página: “o que é um diagrama de Venn?”Embora John Venn popularizado representando a teoria dos conjuntos com círculos sobrepostos, as ideias e símbolos nos diagramas de Venn realmente o antecederam.
uma palavra rápida
Se você tem seguido em Lucidchart, você percebeu que é a solução ideal para diagramas de Venn. Como você está editando na nuvem, você pode facilmente colaborar com colegas, importar imagens e compartilhar seus diagramas digitalmente ou através de impressão.
ver como funciona o nosso fabricante de diagramas Venn.
Saiba mais