regressão à média é um fenômeno estatístico comum que pode nos induzir em erro quando observamos o mundo. Aprender a reconhecer quando a regressão à média está em jogo pode nos ajudar a evitar má interpretação de dados e ver padrões que não existem.

**

é importante minimizar os casos de mau julgamento e abordar os pontos fracos do nosso raciocínio. Aprender sobre a regressão ao meio pode ajudar-nos.o psicólogo vencedor do Prémio Nobel Daniel Kahneman escreveu um livro sobre preconceitos que toldam o nosso raciocínio e distorcem a nossa percepção da realidade. Acontece que há todo um conjunto de erros lógicos que cometemos porque a nossa intuição e cérebro não lidam bem com estatísticas simples. Um dos erros que ele examina no pensamento rápido e lento é a regressão infame em direção à média.

A noção de regressão à média foi primeiramente trabalhada por Sir Francis Galton. A regra diz que, em qualquer série com fenômenos complexos que dependem de muitas variáveis, onde o acaso está envolvido, os resultados extremos tendem a ser seguidos por mais moderados.na busca da sabedoria, Peter Bevelin oferece o exemplo de John, que estava insatisfeito com o desempenho de novos empregados, então ele colocou-os em um programa de aumento de habilidades onde ele mediu a habilidade dos empregados:

suas pontuações são agora mais altas do que estavam no primeiro teste. John’s conclusion: “The skill-enhancing program caused the improvement in skill.”Isto não é necessariamente verdade. Suas pontuações mais altas podem ser o resultado de regressão à média. Uma vez que estes indivíduos foram medidos como estando na extremidade baixa da escala da habilidade, eles teriam mostrado uma melhoria mesmo se não tivessem tomado o programa de aumento da habilidade. E pode haver muitas razões para o seu desempenho anterior-estresse, fadiga, doença, distração, etc. A sua verdadeira capacidade talvez não tenha mudado.

nosso desempenho varia sempre em torno de algum desempenho médio verdadeiro. O desempenho extremo tende a ficar menos extremo da próxima vez. Por quê? As medições de teste nunca podem ser exatas. Todas as medições são feitas de uma parte verdadeira e uma parte de erro aleatório. Quando as medições são extremas, é provável que sejam parcialmente causadas por acaso. É provável que o Chance contribua menos na segunda vez que medimos o desempenho.

se mudarmos de uma maneira de fazer algo para outra simplesmente porque não temos sucesso, é muito provável que façamos melhor da próxima vez, mesmo que a nova maneira de fazer algo seja igual ou pior.

esta é uma das razões pelas quais é perigoso extrapolar de pequenas dimensões de amostras, uma vez que os dados podem não ser representativos da distribuição. É também por isso que James March argumenta que quanto mais tempo alguém permanece em seu trabalho, ” quanto menor a diferença provável entre o registro observado de desempenho e capacidade real.”Tudo pode acontecer a curto prazo, especialmente em qualquer esforço que envolva uma combinação de habilidade e sorte. (A relação entre habilidade e sorte também afeta a regressão à média.)

regressão à média

os efeitos da regressão à média podem ser frequentemente observados nos desportos, onde o efeito causa muitas especulações injustificadas.ao pensar rápido e devagar, Kahneman lembra de ver o salto de ski dos homens, uma disciplina onde a pontuação final é uma combinação de dois saltos separados. Ciente da regressão à média, Kahneman foi surpreendido ao ouvir as previsões do comentarista sobre o segundo salto. Ele escreve:

a Noruega tinha um grande primeiro salto; ele vai ser tenso, esperando para proteger a sua liderança e provavelmente vai fazer pior” ou “a Suécia tinha um mau primeiro salto e agora ele sabe que não tem nada a perder e vai ser relaxado, o que deve ajudá-lo a fazer melhor.

Kahneman aponta que o comentador tinha notado a regressão à média e surgiu com uma história para a qual não havia evidência causal (ver falácia narrativa). Isto não quer dizer que a sua história não pudesse ser verdadeira. Talvez, se medirmos os batimentos cardíacos antes de cada salto, veremos que eles estão mais relaxados se o primeiro salto foi ruim. No entanto, a questão não é essa. A questão é que a regressão à média acontece quando a sorte desempenha um papel, como aconteceu no resultado do primeiro salto.

a lição do desporto aplica-se a qualquer actividade onde o acaso desempenha um papel. Muitas vezes atribuímos explicações da nossa influência sobre um determinado processo ao progresso ou à falta dele.

na realidade, a ciência do desempenho é complexa, dependente da situação e muitas vezes muito do que pensamos estar dentro do nosso controle é verdadeiramente aleatório.no caso de saltos de esqui, um vento forte contra o saltador levará até o melhor atleta mostrando resultados medíocres. Da mesma forma, um vento forte e condições de esqui em favor de um saltador medíocre pode levar a um considerável, mas um alto temporário em seus resultados. Estes efeitos, no entanto, desaparecerão quando as condições mudarem e os resultados regressarem ao normal.

isto pode ter implicações graves para o treino e acompanhamento do desempenho. As regras de regressão sugerem que, ao avaliar o desempenho ou contratação, devemos confiar em registros de pista mais do que resultados de situações específicas. Caso contrário, somos propensos a ficar desapontados.quando Kahneman estava dando uma palestra à Força Aérea Israelense sobre a psicologia de treinamento efetivo, um dos oficiais compartilhou sua experiência de que estender o louvor a seus subordinados levou a pior performance, enquanto que repreensão levou a uma melhoria nos esforços subsequentes. Como consequência, ele tinha crescido a ser generoso com feedback negativo e tornou-se bastante cauteloso de dar muito elogio.Kahneman imediatamente percebeu que era regressão à média no trabalho. Ele ilustrou o equívoco através de um simples exercício que você pode querer experimentar a si mesmo. Ele desenhou um círculo em um quadro-negro e, em seguida, pediu aos oficiais, um a um, para jogar um pedaço de giz no centro do círculo com suas costas voltadas para o quadro-negro. Ele então repetiu a experiência e gravou o desempenho de cada oficial no primeiro e segundo julgamento.

naturalmente, aqueles que fizeram incrivelmente bem na primeira tentativa tendem a fazer pior em sua segunda tentativa e vice-versa. A falácia imediatamente se tornou clara: a mudança no desempenho ocorre naturalmente. Isso mais uma vez não quer dizer que o feedback não importa de todo – talvez faça, mas o oficial não tinha nenhuma evidência para concluir que fez.

a correlação imperfeita e a Chance

neste ponto, você pode estar se perguntando Por que a regressão à média acontece e como podemos ter certeza que estamos cientes dela quando ela ocorre.

A fim de compreender a regressão à média, devemos primeiro compreender a correlação.

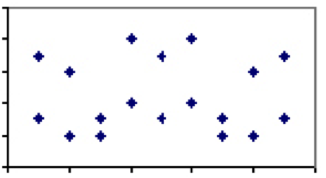
O coeficiente de correlação entre duas medidas que varia entre -1 e 1, é uma medida do peso relativo dos fatores que compartilham. Por exemplo, dois fenômenos com poucos fatores compartilhados, como o consumo de água engarrafada versus taxa de suicídio, devem ter um coeficiente de correlação de quase 0. Ou seja, se olhássemos para todos os países do mundo e traçássemos taxas de suicídio de um ano específico contra o consumo per capita de água engarrafada, a parcela não mostraria qualquer padrão.

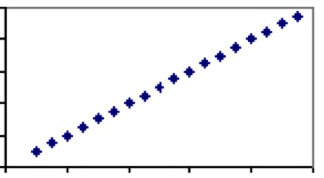
ao contrário, há medidas que são exclusivamente dependentes do mesmo fator. Um bom exemplo disso é a temperatura. O único fator que determina a temperatura-velocidade das moléculas-é compartilhado por todas as escalas, portanto cada grau em Celsius terá exatamente um valor correspondente em Fahrenheit. Portanto, a temperatura em Celsius e Fahrenheit terá um coeficiente de correlação de 1 e a parcela será uma linha reta.

Há poucos fenômenos na área de ciências humanas que têm um coeficiente de correlação de 1. Há, no entanto, abundância onde a associação é fraca a moderada e há algum poder explicativo entre os dois fenômenos. Considere a correlação entre altura e peso, que aterrissaria em algum lugar entre 0 e 1. Enquanto virtualmente cada criança de três anos será mais leve e menor do que qualquer homem adulto, nem todos os homens adultos ou crianças de três anos da mesma altura pesarão o mesmo.

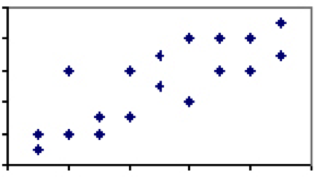
Esta variação e o correspondente menor grau de correlação implica que, enquanto a altura é geralmente um bom indicador, há, claramente, são outros factores que não a altura em jogo. Quando a correlação de duas medidas é menos do que perfeita, devemos estar atentos aos efeitos da regressão à média.

Kahneman observou uma regra geral: sempre que a correlação entre duas pontuações é imperfeita, haverá regressão à média.

isto no início pode parecer confuso e não muito intuitivo, mas o grau de regressão à média está diretamente relacionado com o grau de correlação das variáveis. Este efeito pode ser ilustrado com um exemplo simples.suponha que você está em uma festa e pergunte por que é que mulheres altamente inteligentes tendem a se casar com homens que são menos inteligentes do que eles. A maioria das pessoas, mesmo aqueles com algum treinamento em estatísticas, irá rapidamente saltar para dentro com uma variedade de explicações causais que vão desde evitar a concorrência aos medos de solidão que estas mulheres enfrentam. Um tema de tal Controvérsia é susceptível de suscitar um grande debate.e se perguntássemos por que razão a correlação entre as pontuações de inteligência dos cônjuges é menos do que perfeita? Esta questão não é tão interessante e há pouco a adivinhar-todos sabemos que isso é verdade. O paradoxo reside no fato de que as duas questões são algebricamente equivalentes. Kahneman explica:

Se a correlação entre a inteligência dos cônjuges é menos do que perfeito (e se os homens e as mulheres, em média, não diferem em termos de inteligência), então ele é um matemático inevitabilidade que, muito inteligente, as mulheres vão ser casada com um marido que são, em média, menos inteligentes que eles são (e vice-versa, claro). A regressão observada à média não pode ser mais interessante ou explicável do que a correlação imperfeita.

assumindo que a correlação é imperfeita, as chances de dois parceiros representando o 1% de topo em termos de qualquer característica é muito menor do que um parceiro representando o 1% de topo e o outro – o 99% de baixo.

a causa, efeito e tratamento

devemos ser especialmente cautelosos com a regressão ao fenômeno médio ao tentar estabelecer a causalidade entre dois fatores. Sempre que a correlação é imperfeita, o melhor sempre parecerá piorar e o pior parecerá melhorar ao longo do tempo, independentemente de qualquer tratamento adicional. Isto é algo que os meios de comunicação social em geral e, por vezes, até cientistas treinados não conseguem reconhecer.

considere o exemplo que Kahneman dá:

Crianças deprimidas tratadas com uma bebida energética melhoram significativamente durante um período de três meses. Eu inventei esta manchete de jornal, mas o facto é que é verdade.: se tratasse um grupo de crianças deprimidas durante algum tempo com uma bebida energética, elas demonstrariam uma melhoria clinicamente significativa. É também o caso de crianças deprimidas que passam algum tempo de pé em sua cabeça ou abraçar um gato por vinte minutos por dia também vai mostrar melhoria.

sempre que se depara com tais títulos, é muito tentador chegar à conclusão de que bebidas energéticas, de pé na cabeça ou abraçando gatos são curas perfeitamente viáveis para a depressão. Estes casos, porém, incorporam mais uma vez a regressão à média:

Crianças deprimidas são um grupo extremo, estão mais deprimidas do que a maioria das outras crianças—e grupos extremos regressam à média ao longo do tempo. A correlação entre as pontuações da depressão em sucessivas ocasiões de testes é menos do que perfeita, então haverá regressão à média: as crianças deprimidas vão ficar um pouco melhor com o tempo, mesmo se não abraçam gatos e não bebem Red Bull.

muitas vezes atribuímos erradamente uma política ou tratamento específico como a causa de um efeito, quando a mudança nos grupos extremos teria acontecido de qualquer maneira. Isto apresenta um problema fundamental: como podemos saber se os efeitos são reais ou simplesmente devido à variabilidade?

felizmente há uma maneira de dizer entre uma melhoria real e regressão à média. Trata-se da introdução do chamado grupo de controlo, que se espera venha a melhorar apenas por regressão. O objetivo da pesquisa é determinar se o grupo tratado melhora mais do que a regressão pode explicar.

em situações da vida real com o desempenho de indivíduos ou equipes específicas, onde o único parâmetro de referência real é o desempenho passado e nenhum grupo de controle pode ser introduzido, os efeitos da regressão pode ser difícil, se não impossível de desengatar. Podemos comparar com a média da indústria, os pares do grupo de coortes ou as taxas históricas de melhoria, mas nenhuma destas medidas é perfeita.

**

felizmente a consciência da regressão ao próprio fenómeno médio já é um grande primeiro passo para uma abordagem mais cuidadosa para a compreensão da Sorte e do desempenho.

Se há alguma coisa a ser aprendida a partir da regressão à média, é a importância dos registros de pista ao invés de depender de histórias de sucesso de uma só vez. Espero que, da próxima vez que se depararem com uma qualidade extrema, em parte governada pelo acaso, compreendam que os efeitos são susceptíveis de regredir ao longo do tempo e ajustem as vossas expectativas em conformidade.

o que ler a seguir

• actualize o seu pensamento com 113 modelos mentais explicados.leia sobre o pensamento de segundo nível para evitar consequências negativas.