Editor Note

the following student research report was prepared for Professor Judit Kardos’ Math 255 class, held at the College of New Jersey. Este foi um curso introdutório de 3 créditos na história da Matemática. Este relatório foi contado para 30% da nota final. É um exemplo do tipo de pesquisa histórica que os estudantes podem fazer usando fontes secundárias.a solução de Leonard Euler para o problema da Ponte de Königsberg Königsberg Königsberg

a nossa história começa no século XVIII, na pitoresca cidade de Königsberg, Prússia nas margens do rio Pregel. Em 1254, os Cavaleiros Teutônicos fundaram a cidade de Königsberg sob a liderança do Rei boêmio Ottoker II após sua segunda cruzada contra os prussianos. Na Idade Média, Königsberg tornou-se uma cidade muito importante e centro de comércio com sua localização estrategicamente posicionada no Rio. Obras de arte do século XVIII mostram Königsberg como uma cidade próspera, onde frotas de navios enchem o Pregel, e seu comércio oferece um estilo de vida confortável tanto para os comerciantes locais e suas famílias. A economia saudável permitiu que as pessoas da cidade construíssem sete pontes através do rio, a maior parte das quais conectadas à Ilha de Kneiphof; suas localizações podem ser vistas na imagem que acompanha .

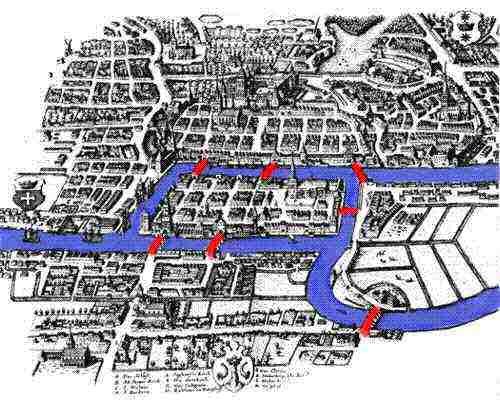
À medida que o rio fluía em torno de Kneiphof, literalmente significando pátio do pub, e outra ilha, dividiu a cidade em quatro regiões distintas. As sete pontes foram chamadas de Ponte do Ferreiro, Ponte de ligação, Ponte Verde, Ponte mercante, Ponte De Madeira, Ponte Alta e Ponte Honey. Segundo a tradição, os cidadãos de Königsberg passavam as tardes de domingo a passear pela sua bela cidade. Enquanto caminhavam, o povo da cidade decidiu criar um jogo para si mesmo, seu objetivo era criar uma maneira em que eles pudessem andar ao redor da cidade, atravessando cada uma das sete pontes apenas uma vez. Embora nenhum dos cidadãos de Königsberg pudesse inventar uma rota que lhes permitisse atravessar cada uma das pontes apenas uma vez, ainda assim não podiam provar que era impossível. Felizmente para eles, Königsberg não estava muito longe de São Petersburgo, casa do famoso matemático Leonard Euler.

Euler and the Bridge Problem

Why would Euler concern himself with a problem so unrelated to the field of mathematics? Por que um matemático tão grande gastaria muito tempo com um problema trivial como o problema da Ponte de Königsberg? Euler era obviamente um homem ocupado, publicando mais de 500 livros e papéis durante sua vida. Só em 1775, escreveu uma média de um trabalho matemático por semana, e durante sua vida escreveu sobre uma variedade de tópicos além da matemática, incluindo mecânica, óptica, Astronomia, navegação e hidrodinâmica. Não é surpreendente que Euler sentiu que este problema era trivial, afirmando em uma carta de 1736 para Carl Leonhard Gottlieb Ehler, prefeito de Danzig, que lhe pediu uma solução para o problema :

. . . Assim você vê, mais nobre Senhor, como este tipo de solução tem pouca relação com a matemática, e eu não entendo por que você espera de um matemático para produzi-lo, ao invés do que qualquer outra pessoa, pois a solução é baseada na razão, e sua descoberta não depende de qualquer princípio matemático. Por causa disso, não sei por que mesmo as questões que têm tão pouca relação com a matemática são resolvidas mais rapidamente pelos matemáticos do que por outros.

apesar de Euler achar o problema trivial, ele ainda estava intrigado com ele. Em uma carta, escrita no mesmo ano Giovanni Marinoni, um italiano, engenheiro e matemático, Euler disse:

Esta pergunta é tão banal, mas me pareceu digno de atenção, em que a geometria, nem álgebra, nem mesmo a arte de contar foi o suficiente para resolvê-lo.

Euler acreditava que este problema estava relacionado a um tópico que Gottfried Wilhelm Leibniz já havia discutido e desejado trabalhar com, algo que Leibniz se refere como geometria situs, ou geometria de posição. Esta chamada geometria da posição é o que agora é chamado de teoria dos grafos, que Euler introduz e utiliza enquanto resolve este famoso problema.em 26 de agosto de 1735, Euler apresenta um artigo contendo a solução para o problema da Ponte Konigsberg. Ele aborda tanto este problema específico, como uma solução geral com qualquer número de massas de terra e qualquer número de pontes. Este artigo, chamado “Solutio problematis ad geometriam situs pertinentis”, foi mais tarde publicado em 1741 . O documento de Euler é dividido em 21 parágrafos numerados, e no que se segue, uma versão simplificada dos parágrafos de Euler será apresentada.nos dois primeiros parágrafos da prova de Euler, ele introduz o problema da Ponte Konigsberg. No parágrafo 1, Euler afirma que acredita que este problema diz respeito à geometria, mas não à geometria bem conhecida por seus contemporâneos, que envolve medições e cálculos, mas em vez disso um novo tipo de geometria, que Leibniz referiu como geometria de posição. Depois, no nº 2, Euler explica à sua audiência como funciona o problema de Konigsberg. Euler forneceu um esboço do problema (ver Figura 1 de Euler), e chamou as sete pontes distintas: A, b, c, d, E, f, E, G. neste parágrafo ele afirma a questão geral do problema, “pode-se descobrir se é possível ou não atravessar cada ponte exatamente uma vez?”

Euler Figura 1 do ‘escopo d problematis ad geometriam situs pertinentis,’ Eneström 53

Depois de declarar a questão geral que ele está tentando resolver, Euler começa a explorar diferentes formas de encontrar uma solução. No parágrafo 3, Euler diz ao leitor que para resolver este problema específico, ele poderia escrever todos os caminhos possíveis, mas esta técnica levaria muito tempo, e não trabalharia para Configurações maiores com mais pontes e massas de terra. Por causa destas questões, Euler decidiu escolher um método diferente para resolver este problema. no parágrafo 4, ele começa a simplificar o problema inventando um sistema conveniente para representar a travessia de uma ponte. Euler decide que em vez de usar as letras minúsculas para representar a travessia de uma ponte, ele iria escrever as letras maiúsculas representando os landmasses. Por exemplo, referenciando sua figura 1, AB significaria uma viagem que começou em landmass A, e terminou em B. Além disso, se depois de viajar de landmass a para B, alguém decide se mudar para landmass D, Isso seria simplesmente denotado, ABD. No parágrafo 5, Euler continua sua discussão sobre este processo explicando que em ABDC, embora haja quatro letras maiúsculas, apenas três pontes foram atravessadas. Euler explica que não importa quantas pontes existem, haverá mais uma carta para representar a travessia necessária. Por causa disso, todo o problema da Ponte de Königsberg exigiu que sete pontes fossem atravessadas e, portanto, oito letras maiúsculas.no parágrafo 6, Euler continua explicando os detalhes de seu método. Ele diz ao leitor que se há mais de uma ponte que pode ser atravessada quando se vai de um landmass para o outro, não importa qual ponte é usada. Por exemplo, embora existam duas pontes, a e b, que podem levar um viajante de A Para B, não importa com a notação de Euler qual ponte é tomada. Neste parágrafo, Euler também discute o problema específico com o qual está lidando. Ele explica, usando sua figura original, que o problema de Königsberg precisa exatamente de oito letras,onde os pares de (A,B) E (A, C) devem aparecer ao lado um do outro exatamente duas vezes, não importa qual letra aparece primeiro. Além disso,os pares (A, D), (B, D), E (C, D) devem ocorrer juntos exatamente uma vez para um caminho que cruza cada ponte uma vez e apenas uma vez para existir.

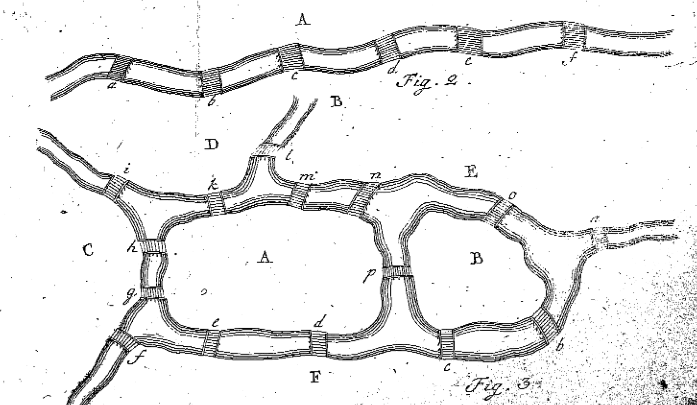
Euler Figuras 2 e 3 de ” escopo d problematis ad geometriam situs pertinentis,’ Eneström 53

No Parágrafo 7, Euler informa o leitor de que ele precisa encontrar um oito-carta seqüência que satisfaz o problema, ou ele precisa provar que não esta sequência existir. Antes que ele faça isso para o problema da Ponte de Königsberg, ele decide encontrar uma regra para descobrir se existe um caminho para um problema mais geral. Ele faz isso no parágrafo 8, olhando para um exemplo muito mais simples de massas de terra e pontes. Euler Desenha a Figura 2, e começa a avaliar as situações em que a região A é atravessada. Euler afirma que se a Ponte a é percorrida uma vez, A Foi onde a viagem começou ou terminou, e portanto foi usada apenas uma vez. Se as pontes A, b E c são todas viajadas uma vez, A é usado exatamente duas vezes, não importa se é o lugar inicial ou final. Da mesma forma, se Cinco Pontes levassem a A, O landmass A ocorreria exatamente três vezes na viagem. Euler afirma que, ” em geral, se o número de pontes é qualquer número ímpar, e se é aumentado por um, então o número de ocorrências de A é metade do resultado.”Em outras palavras, se houver um número ímpar de pontes ligando A a outras massas de terra, adicione uma ao número de pontes, e divida-as por duas, para descobrir quantas vezes totais A deve ser usado no caminho, onde cada ponte é usada uma vez e apenas uma vez (i.e. Ocorrências totais de A onde A tem um # ímpar de pontes = (#de pontes – 1) / 2 ). usando este facto, Euler resolve o problema da ponte de Königsberg no parágrafo 9. Nesse caso, uma vez que há cinco pontes que levam a A, ela deve ocorrer três vezes (veja sua figura 1, acima). Da mesma forma, B, C E D devem aparecer duas vezes, pois todos eles têm três pontes que os levam a eles. Portanto 3 (para a) + 2(para b) + 2(para C) + 2 (para D) = 9, mas Euler já afirmou que só deve haver oito ocorrências para as sete pontes. Isto é uma contradição! Portanto, é impossível viajar as pontes na cidade de Königsberg uma vez e só uma vez. Fim, ou é? Embora o povo de Königsberg possa estar satisfeito com esta solução, o grande matemático Leonhard Euler não ficou satisfeito. Euler continua sua prova de lidar com situações mais gerais.

Euler Generalização

No Parágrafo 10, Euler continua sua discussão observando que, se a situação envolve todas as massas de terra com um número ímpar de pontes, é possível dizer se uma viagem pode ser feita usando cada ponte apenas uma vez. Euler afirma que se a soma do número de vezes que cada letra deve aparecer é mais uma, Então o número total de pontes, uma viagem pode ser feita. No entanto, se o número de ocorrências for maior do que um a mais do que o número de pontes, não se pode fazer uma viagem, como o problema da Ponte de Königsberg. Isto porque a regra, que Euler dá para um número ímpar de pontes, usando sua figura 2, é verdadeira para a situação geral se há apenas um outro landmass ou mais de um.nos pontos 11 e 12, Euler trata da situação em que uma região tem um número par de pontes ligadas a ela. Esta situação não aparece no problema de Königsberg e, por conseguinte, tem sido ignorada até agora. Na situação com um landmass X com um número par de pontes, dois casos podem ocorrer. O primeiro caso é quando X é o ponto de partida para a viagem. Neste caso, X aparecerá duas vezes, uma Como o ponto de partida, e outra como o ponto final. No outro caso, X não é o ponto de partida. Se isso acontecesse, X só apareceria uma vez, pois a viagem teria que entrar através de uma ponte e imediatamente sair através da única outra disponível. Da mesma forma, se há quatro pontes anexadas a X o número de ocorrências de X depende se é ou não um ponto de partida. Se a viagem começa em X, ela deve aparecer três vezes, mas se ela não começar em X, ela só aparecerá duas vezes. Assim, em geral, Se X tem um número par de pontes anexadas, então se a viagem não começa em X, X aparece metade do número de vezes como pontes (i.e. Ocorrências de X onde X é par e não o ponto de partida = (#de pontes) / 2). Se a viagem começa em X então X aparece metade do número de vezes como pontes, mais uma (ou seja, ocorrências de X onde X é par e ponto de partida = (#de pontes) / 2) + 1).

nos parágrafos 13 a 15, Euler explica como descobrir se existe um caminho usando cada ponte uma vez e apenas uma vez e apresenta o seu próprio exemplo para mostrar como funciona. Euler primeiro explica seu método simples de seis etapas para resolver qualquer situação geral com massas de terra divididas por rios e conectadas por pontes. O primeiro Euler denota cada landmass com uma letra maiúscula. Em segundo lugar, ele pega o número total de pontes, adiciona uma, e escreve isso acima do gráfico que ele está prestes a fazer. Em seguida, ele pega as letras maiúsculas, coloca – as em uma coluna, e ao lado deles escreve o número de pontes. Em quarto lugar, ele indica com asteriscos as massas de terra que têm um número par de pontes. Então, ao lado de cada número par, ele escreve ½ do número e ao lado de cada número ímpar ele coloca ½ o número mais um. Finalmente, Euler adiciona os números escritos na coluna mais direita e se a soma for uma menor do que, ou igual a, o número de pontes mais uma, então a jornada necessária é possível. É importante notar, no entanto, que se a soma for uma a menos do que o número de pontes mais uma, então a viagem deve começar a partir de um dos landmasses marcados com um asterisco. Se a soma for igual ao número de pontes mais uma, a viagem deve começar numa região não marcada com asterisco.

exemplos

Usando o problema de Konigsberg como o seu primeiro exemplo Euler mostra o seguinte:

Número de pontes = 7, o Número de pontes de mais um = 8

Região de Pontes Vezes Região Deve Aparecer

5 3

B 3 2

C 3 2

D 3 2

no Entanto, 3 + 2 + 2 + 2 = 9, que é mais do que 8, assim, a viagem é impossível.como este exemplo é bastante básico, Euler decide projetar sua própria situação com duas ilhas, quatro rios e quinze pontes. A situação criada por Euler pode ser vista em sua figura 3, acima. Euler agora tenta descobrir se existe um caminho que permite a alguém passar por cada ponte uma vez e só uma vez. Euler segue os mesmos passos acima, nomeando-as em cinco regiões diferentes, com letras maiúsculas, e cria uma tabela para verificar se ela é possível, como o seguinte:

Número de pontes = 15, Número de pontes de mais um = 16

Região de Pontes Vezes Região Deve Aparecer

A* 8 4

B* 4 2

C* 4 2

D 3 2

E 5 3

F* 6 3

além, 4 + 2 + 2 + 2 + 3 + 3 = 16, que é igual ao número de pontes, mais um, o que significa que a viagem é, de fato, possível. Uma vez que a soma é igual ao número de pontes mais uma, a viagem deve começar em D ou E. Agora que Euler sabe que é possível fazer uma viagem, tudo o que precisa de fazer é indicar qual será o caminho. Euler escolhe o caminho Eafbcfdaeffcgahcidkamenapboeld, onde ele inclui quais pontes são cruzadas entre as cartas que representam as massas de terra. Embora esta informação seja estranha, como a ponte exata não importa em saber que uma viagem é possível, é útil ao selecionar um caminho. Este é um bom exemplo que mostra o método que Euler usaria para resolver qualquer problema desta natureza. nas conclusões de Euler nos parágrafos seguintes, Euler apresenta outra maneira de descobrir se uma viagem pode ser feita em qualquer conjunto de massas de terra, pontes e rios. No parágrafo 16, Euler ressalta que o total dos números listados diretamente à direita dos landmasses totaliza o dobro do número total de pontes. Este fato mais tarde se torna conhecido como o lema do aperto de mão. Basicamente, o lema do handshaking afirma que cada ponte é contada duas vezes, uma para cada landmass a que está ligada. No parágrafo 17, Euler continua a afirmar que a soma de todas as pontes que conduzem a cada região é igual, uma vez que metade deste número é igual ao número total de pontes. No entanto, isso é impossível se houver um número ímpar de massas de terra com um número ímpar de pontes. Portanto, Euler prova que se há alguns números ímpares ligados às massas de terra, deve haver um número par desses massas de terra.

no entanto, isto não é suficiente para provar quando há um caminho onde cada ponte é usada uma e apenas uma vez, como o problema da Ponte de Königsberg tem um número par de massas de terra com um número ímpar de pontes indo para eles. Por esta razão, a Euler acrescenta mais restrições aos pontos 18 e 19. Euler explica que, uma vez que o total dos números de pontes anexadas a cada massa de terra é igual ao dobro do número de pontes (como visto no lema do handshaking), portanto, se você adicionar dois a esta soma e, em seguida, dividir por dois, você vai obter o número de pontes totais mais um. Este número é o mesmo usado antes, que é usado para dizer se um caminho é possível. Se todos os números são pares, então a terceira coluna na tabela somará a menos um do que o número total de pontes mais um.

Euler então explica que é óbvio que se existem dois landmasses com um número ímpar de pontes, então a viagem será sempre possível se a viagem começar em uma das regiões com um número ímpar de pontes. Isto porque se os números pares forem reduzidos para metade, e cada um dos ímpares for aumentado para uma e metade, a soma destas metades será igual a mais uma, Então o número total de pontes. No entanto, se há quatro ou mais landmasses com um número ímpar de pontes, então é impossível que haja um caminho. Isto é porque a soma das metades dos números ímpares mais um junto com a soma de todas as metades dos números pares fará a soma da terceira coluna maior do que o número total de pontes mais um. Portanto, Euler acabou de provar que pode haver, no máximo, dois landmasses com um número ímpar de pontes. com isso sendo afirmado, Euler pode agora fazer suas conclusões sobre formas mais gerais do problema da Ponte de Königsberg. No parágrafo 20, Euler dá as três diretrizes que alguém pode usar para descobrir se um caminho existe usando cada ponte uma vez e apenas uma vez. Primeiro, ele afirmou que se há mais de duas massas de terra com um número ímpar de pontes, então nenhuma viagem é possível. Em segundo lugar, se o número de pontes é ímpar para exatamente dois landmasses, então a viagem é possível se ela começa em um dos dois landmasses numerados ímpares. Finalmente, Euler afirma que se não houver regiões com um número ímpar de massas de terra, então a viagem pode ser realizada a partir de qualquer região. Depois de afirmar estes três fatos, Euler conclui sua prova com o parágrafo 21, que simplesmente afirma que depois de se perceber que existe um caminho, eles ainda devem passar pelo esforço para escrever um caminho que funciona. Euler acreditava que o método para realizar isso era trivial, e ele não queria gastar muito tempo nele. No entanto, Euler sugeriu concentrar-se em como chegar de um landmass para o outro, em vez de concentrar-se nas pontes específicas no início.

a prova e a teoria dos grafos de Euler

ao ler a prova original de Euler, descobre-se um trabalho relativamente simples e facilmente compreensível da matemática; no entanto, não é a prova real, mas os passos intermediários que tornam este problema famoso. A grande inovação de Euler foi ver o problema da ponte de Königsberg de forma abstracta, usando linhas e cartas para representar a maior situação de massas de terra e pontes. Ele usou letras maiúsculas para representar massas de terra, e letras minúsculas para representar pontes. This was a completely new type of thinking for the time, and in his paper, Euler accidentally sparked a new branch of mathematics called graph theory, where a graph is simply a collection of vertices and edges. Hoje um caminho em um grafo, que contém cada aresta do grafo uma vez e somente uma vez, é chamado de um caminho Euleriano, por causa deste problema. Desde o tempo em que Euler resolveu este problema até hoje, a teoria dos grafos tornou-se um ramo importante da matemática, que guia a base de nosso pensamento sobre redes.

A Ponte de Königsberg problema é por Biggs estados ,

As origens da teoria dos grafos são humildes, mesmo frívolo … Os problemas que levaram ao desenvolvimento da teoria de grafos foram muitas vezes pouco mais do que quebra-cabeças, projetado para testar a criatividade em vez de estimular a imaginação. Mas apesar da trivialidade aparente de tais quebra-cabeças, eles capturaram o interesse dos matemáticos, com o resultado de que a teoria dos grafos se tornou um assunto rico em resultados teóricos de uma surpreendente variedade e profundidade.

como a afirmação de Biggs implicaria, este problema é tão importante que é mencionado no primeiro capítulo de cada livro da teoria dos grafos que foi perusado na biblioteca.

Após a descoberta de Euler (ou invenção, dependendo de como o leitor olha para ele), a teoria dos grafos cresceu com grandes contribuições feitas por grandes matemáticos como Augustin Cauchy, William Hamilton, Arthur Cayley, Gustav Kirchhoff, e George Polya. Estes homens contribuíram para descobrir ” quase tudo o que é conhecido sobre grafos grandes, mas ordenados, como a estrutura formada por átomos em um cristal ou a estrutura hexagonal feita por abelhas em uma colmeia . Outros problemas famosos da teoria dos grafos incluem encontrar uma maneira de escapar de um labirinto ou labirinto, ou encontrar a ordem de movimentos com um cavaleiro em um tabuleiro de xadrez de tal forma que cada quadrado é desembarcado apenas uma vez e o cavaleiro retorna ao espaço no qual ele começou . Alguns outros problemas da teoria dos grafos não foram resolvidos por séculos .

the Fate of Königsberg

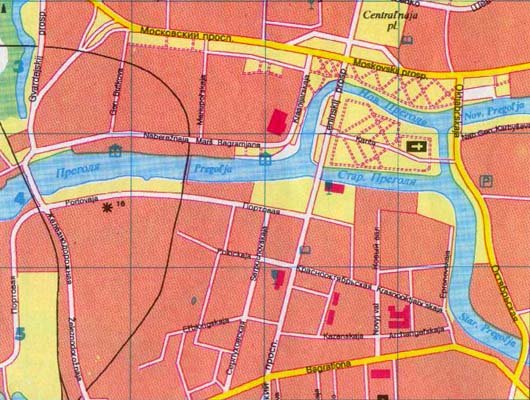
While graph theory boomed after Euler solved the Königsberg Bridge problem, the town of Königsberg had a much different fate. Em 1875, o povo de Königsberg decidiu construir uma nova ponte, entre os nós B E C, aumentando o número de ligações destes dois landmasses para quatro. Isto significava que apenas dois landmasses tinham um número ímpar de ligações, o que dava uma solução bastante simples para o problema. A criação da ponte extra pode ou não ter sido subconscientemente causada pelo desejo de um caminho para resolver o famoso problema da cidade. no entanto, uma nova ponte não resolveu todos os problemas futuros de Königsberg, como a cidade não esperava no século XIX, “o destino triste e devastado pela guerra que a aguardava como sede de uma das batalhas mais ferozes da Segunda Guerra Mundial. Durante quatro dias em agosto de 1944, bombardeiros britânicos destruíram a cidade velha e as partes norte de Königsberg. Em janeiro e fevereiro de 1945, a região em torno de Königsberg está cercada por forças russas. Os civis alemães começam a evacuar da cidade, mas movem-se tarde demais. Milhares de pessoas são mortas tentando fugir de barco e a pé através das águas geladas da Lagoa Curônica. Em abril de 1945, o Exército Vermelho captura Königsberg com cerca de noventa por cento da Cidade Velha em ruínas. o mapa actual de Königsberg é apresentado a seguir . Este mapa mostra o quanto a cidade mudou. Muitas das pontes foram destruídas durante os bombardeios, e a cidade não pode mais fazer a mesma pergunta intrigante que eles foram capazes de fazer no século XVIII. Juntamente com um layout muito diferente, a cidade de Königsberg tem um novo nome, Kaliningrado, com o rio Pregel renomeado Pregolya . Enquanto o destino de Königsberg é terrível, o velho problema dos cidadãos de atravessar cada uma das suas antigas sete pontes exatamente uma vez levou à formação de um ramo completamente novo da matemática, a teoria dos grafos.

Biggs, Norman L., E. K. Lloyd, and Robin J. Wilson. Graph Theory: 1736-1936. Oxford: Clarendon Press, 1976.Dunham, William. O mestre de todos nós. Feira: The Mathematical Association of America, 1999.

Euler, Leonhard, ‘Solutio problematis ad geometriam situs pertinentis’ (1741), Eneström 53, Maa Euler Archive.

“History of Mathematics: On Leonhard Euler (1707-1783).”ScienceWeek (2003). 6 Nov. 2005.

Hopkins, Brian, and Robin Wilson. “The Truth about Königsberg.”College Mathematics Journal (2004), 35, 198-207. Pontes Konigsberg.”The MacTutor History of Mathematics Archive:
http://www-history.mcs.st- and.ac.uk/history/Miscellaneous/other_links/Konigsberg.html Nota do Editor: Este artigo foi originalmente publicado no volume 3 (2006) da Convergence.