9. Impedância e ângulo de fase
não falhe…
Explore impedance, current and voltage in an RLC circuit in the applet later on this page.
Impedância
a impedância de um circuito é a resistência efetiva total ao fluxo de corrente por uma combinação dos elementos do circuito.símbolo: Z
unidades: `Ω`
A tensão total em todos os 3 elementos (resistores, capacitores e indutores) está escrito
VRLC
Para encontrar esta tensão total, nós não podemos apenas adicionar as tensões VR, VL e VC.
Devido a VL e VC são considerados imaginário quantidades, temos:
Impedância VRLC = IZ
Então, `Z = R + j(X_L− X_C)`
Agora, a magnitude (tamanho, ou valor absoluto) de Z é dada por:
`|Z|=sqrt(R^2+(X_L-X_C)^2`
ângulo de Fase
`tan\ theta=(X_L-X_C)/R`
o Ângulo θ representa o ângulo de fase entre a corrente e a tensão.
Compare isso com o ângulo de fase que conhecemos anteriormente em Grafos de y = a sin (bx + c).
exemplo 1
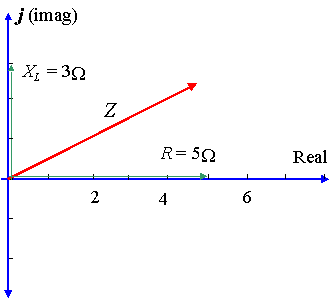
um circuito tem uma resistência de ‘5\ Ω’ EM série com uma reactância em um indutor de `3\ Ω`. Representar a impedância por um número complexo, em forma polar.
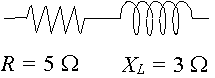
Resposta
neste caso, `X_L= 3\ Ω` e `X_C= 0` para `X_L – X_C= 3\ Ω`.
Então, em forma retangular, a impedância está escrito:
`Z = 5 + 3j\ Ω`
Usando a calculadora, a magnitude de Z é dada por: `5.83`, e o ângulo `θ` (a diferença de fase) é dada por: `de 30,96^@`.
de modo que a tensão leva a corrente em `30.96^@’, como mostrado no diagrama.
apresentando Z como um número complexo( em forma polar), temos:
`Z = 5.83 30 30.96^@\ Ω`.
Exemplo 2(a)
Um determinado circuito de ca tem um resistor de “4\ Ω`, uma reatância através de um indutor de” 8\ Ω` e uma reatância através de um capacitor de `11\ Ω`. Expressa a impedância do circuito como um número complexo em forma polar.
resposta
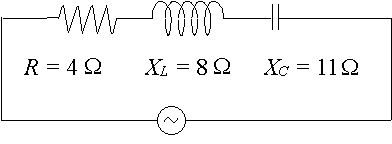
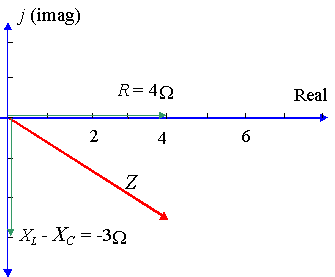
neste caso, temos: `X_L – X_C= 8 – 11 = -3\ Ω`
Então, `Z = 4 – 3j\ Ω` na forma retangular.
Agora, para expressá-lo na forma polar:
Usando a calculadora, encontramos `r = 5` e ` θ = -36.87^@`.
Então, `Z = 5 ∠ -36.87^@\ Ω`
Interativo RLC gráfico
Abaixo está um gráfico interativo para jogar (não é uma imagem estática). Você pode explorar o efeito de um resistor, capacitor e indutor na impedância total em um circuito de AC.
actividades para este interactivo
- Em Primeiro Lugar, Basta brincar com as barras deslizantes. Você pode:
Arraste o controle deslizante superior para a esquerda ou para a direita para variar a impedância devido ao resistor, `R`,
Arraste o XL controle deslizante para cima ou para baixo para variar a impedância devido ao indutor, `X_L`, e
Arraste o XC controle deslizante para cima ou para baixo para variar a impedância devido ao capacitor, `X_C`. - Observe os efeitos de diferentes impedâncias nos valores de XL-XC e Z.
- Observe os efeitos de diferentes impedâncias Sobre θ, o ângulo que a linha de “resultado” vermelha faz com a horizontal (em radianos).
- considere os gráficos de tensão e corrente no interativo. Observe a quantidade de lag ou chumbo à medida que você muda os sliders.o que aprendeu a brincar com esta interactividade?