2.5: A Lei de Darcy – Flow em um meio poroso
a lei de Darcy é crucial para entender muitos ramos da geologia, especialmente a hidrogeologia. Antes de olharmos para a lei e o que ela pode nos dizer, vamos ver como ela foi desenvolvida. A lei de Darcy é nomeada em homenagem a Henry Darcy, um engenheiro francês do século XIX que desenvolveu um sistema subterrâneo de tubos pressurizados para entregar água em torno da cidade de Dijon. O sistema, que também forneceu água para as famosas fontes de Dijon, revolucionou os sistemas de água da cidade e esgoto. O sistema não necessitava de bombas e era conduzido puramente pela gravidade. Durante o processo de desenvolvimento do novo sistema, Darcy conduziu uma série de experimentos onde ele tentou mover a água apenas usando a gravidade.
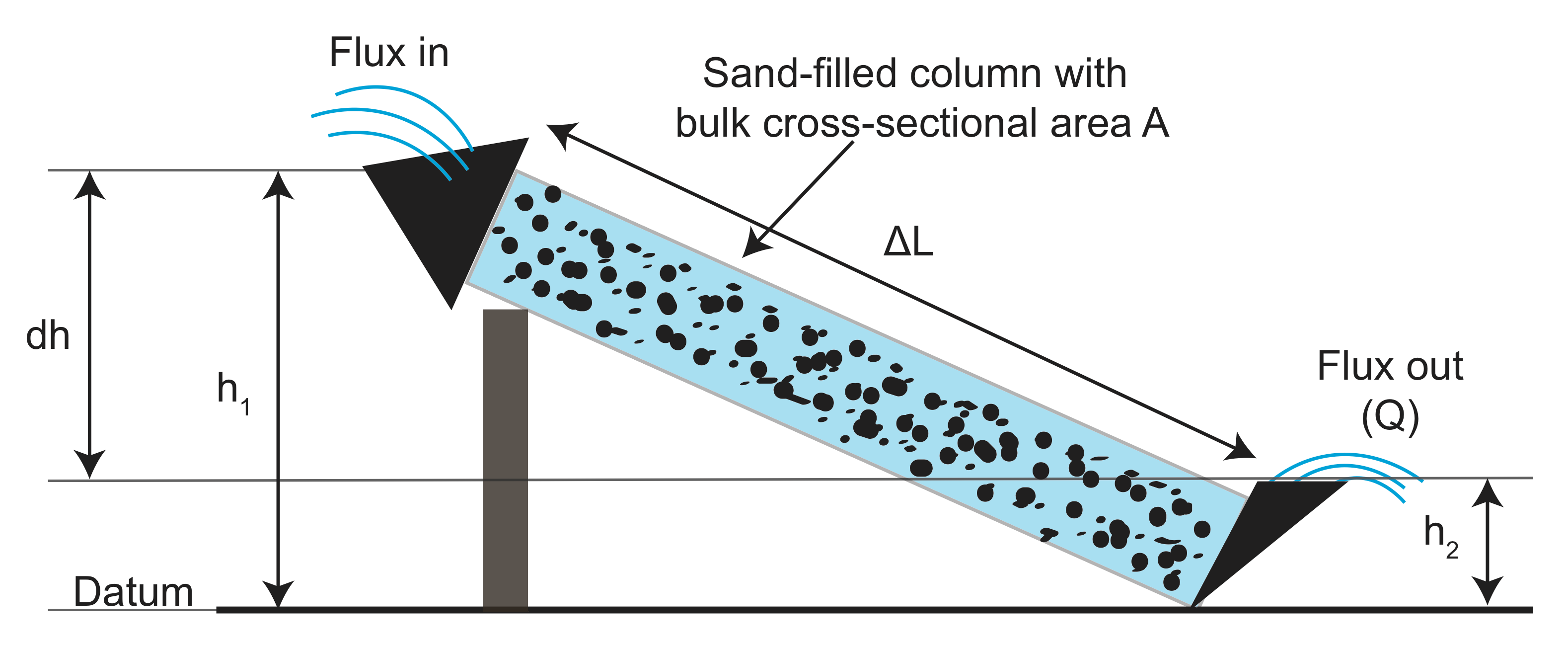
a Partir de experimentos, os dados recolhidos sobre o comprimento do canal (\(L\)), a área da seção transversal do canal (\(A\)), a diferença de altura (\(h_1 – h_2\)), e o fluxo de água que sai \(P\) com e sem granular (filtragem) do material no canal. Ele então plotou a medição do fluxo normalizada pela área versus a razão da diferença de altura para o comprimento da chaminé (\( \frac{h_1 – h_2}{l}\)). O que ele descobriu é que há uma relação linear, e a inclinação depende do material granular que ele usou no canal:
\
o que pode ser reescrito como um derivado,
\
onde \(K\) é a condutividade hidráulica e \(\frac{dh}{dx}\) é o gradiente hidráulico. \(Q\), A taxa de descarga total, tem unidades de \(\frac{m^3}{s}\), o volume de água por tempo. O sinal negativo é devido ao fato de que o fluido flui para baixo (negativo) o gradiente Hidráulico de valores mais elevados para valores mais baixos.
A condutividade hidráulica é um parâmetro físico que explica a facilidade com que o fluido pode mover-se através do espaço poro para o material. Nas experiências originais de Darcy, ele usou areias com diferentes tamanhos de grãos, no entanto, a condutividade hidráulica pode ser determinada para rochas sólidas, bem como, como a maioria das rochas tem algum espaço poro.seguindo os experimentos originais de Darcy, mais trabalho foi feito para entender as propriedades físicas do fluido e da rocha que determinam a condutividade hidráulica efetiva. A partir desses experimentos verificou-se que,
\
onde \(k\) é a permeabilidade intrínseca do meio poroso (sólido), \(\eta\) é a viscosidade dinâmica do fluido, e \(\gamma = \rho g\) é o peso específico do fluido, a qual depende da densidade do fluido, \(\rho\) e de gravidade, de \(g\).
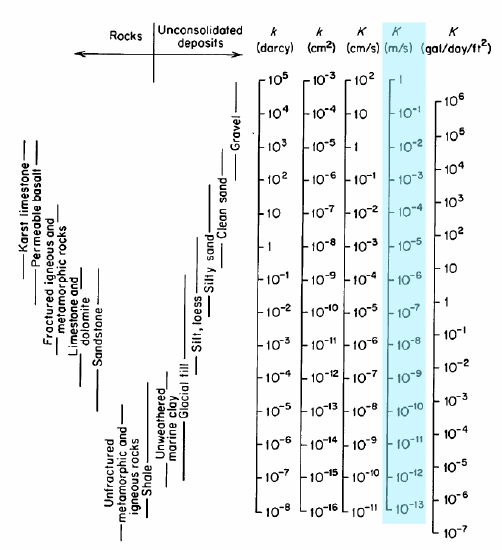
a coluna seleccionada na figura é K, A condutividade hidráulica em \(\frac{m}{s}\); Estas são as unidades que vamos usar. A condutividade hidráulica também é por vezes relatada em termos de permeabilidade intrínseca, \(k\), com unidades de darcys ou cm2. A gama completa de valores para a condutividade hidráulica é de 1-10-13 \(\frac{m}{s}\). Experiências como as da Darcy são usadas para medir K em materiais reais.
A taxa de descarga \(P\) é um volume de fluxo (\(m^3/s\)), mas nós geralmente pensamos de fluxo de fluidos em termos de velocidade ou velocidade. A descarga perguntas podem ser reorganizadas dividindo-se através da área para definir o Fluxo de Darcy
\ \]
Ou em termos de permeabilidade intrínseca e gradiente de pressão,
\
onde \(\eta\) é a viscosidade do fluido (veja abaixo a derivação da segunda equação).é importante notar que o fluxo de Darcy não iguala a velocidade do fluido, embora esteja em unidades de velocidade. A velocidade do fluido é encontrada através da velocidade linear média (\(v_a\)), que é a média da velocidade de todos os caminhos de fluido possíveis através do meio poroso: mas encontrar este valor está fora do âmbito desta classe. Em vez disso, vamos notar que a velocidade do fluido é
\
onde \(\varphi\) é a porosidade e v é a velocidade do fluido. A porosidade, \(\varphi\) é calculada como razão entre o volume de espaço vazio e o volume total de um material \(\varphi=\frac{V_{void}}} {V_{tot}}}\), e é normalmente expressa como uma fracção entre 0 e 1 ou como uma percentagem. Note que se \(\varphi\leq\) 1 então a velocidade do fluido é maior o fluxo de darcy.outro termo que surge quando se discute o fluxo através de rochas e materiais não consolidados é permeabilidade. Enquanto a porosidade é a fração real de poros (vazios) na rocha, esses vazios podem ter diferentes formas e conectividade, o que afeta a facilidade com que um fluido pode se mover através do espaço de poros. A permeabilidade é uma medida da facilidade com que líquidos e gases podem passar através de uma rocha. Quanto mais consolidado o material, menor a sua permeabilidade. Assim, materiais “soltos” como cascalho têm alta permeabilidade. Algumas rochas também podem ter permeabilidade anisotrópica, o que significa que os fluidos podem fluir facilmente em uma direção, mas não em outra. Um exemplo de uma rocha com permeabilidade anisotrópica é um xisto. Os fluidos podem mover-se facilmente dentro de uma camada do Xisto, mas não podem mover-se através de camadas.
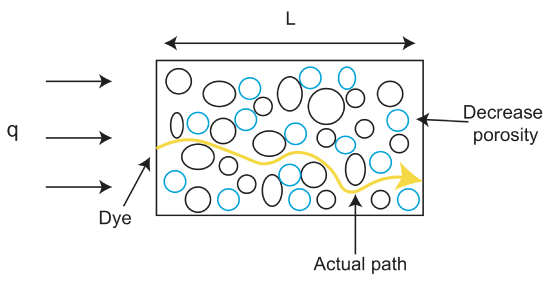
Velocidade do fluido
Let’s do a basic example.
é-nos dado que \(q=2\frac{m}{min}\) e \(\varphi\) é 25% e quer encontrar a velocidade do fluido.primeiro convertemos 25% para 0, 25.
então, \(v= \ frac{2}{0.25}\frac{m}{min}\)
E
\(v=8 \frac{m}{min}\) é a velocidade do fluido.retornando às experiências de Darcy, Qual é o processo físico que está realmente impulsionando o fluxo de fluido através da chaminé?
o termo \(\frac{dh}{dx} \) é referido como a cabeça hidráulica, que é a pressão líquida devido ao peso de um fluido em relação a algum local de referência: um gradiente de pressão. No entanto, \(\frac{dh}{dx} \) não tem unidades de pressão por unidade de comprimento, então por que é chamado de cabeça hidráulica?vamos considerar qual é a pressão na chaminé nas experiências de Darcy. A fim de fazer experiências, de Darcy tinha um tanque de água na extremidade superior da calha oferecendo um nível constante de água na parte superior do canal, o equivalente a altura do canal, \(h_1\). Da mesma forma, havia um tanque no fundo com um nível constante de água equivalente a \(h_2\). Portanto, a pressão do fluido em cada um dos tanques devido ao peso da água é dada por \(P = \rho g h\). O gradiente de pressão entre o topo e a parte inferior da pluma é, em seguida,
\
ou
\
Substituindo na Lei de Darcy,
\ &=\frac{K}{\rho g}\frac{dp}{dx} \end{align}. \]
Recall, a partir de cima que a condutividade hidráulica pode ser escrito em termos da permeabilidade intrínseca como \(K = k\frac{\gamma}{\eta}\), que é equivalente a \(k\frac{\rho g}{\eta} \) ou reorganização, \(\frac{K}{\rho g} = \frac{k}{\eta} \). Portanto, podemos substituir a dar duas expressões equivalentes para Darcy da Lei, com um interms do gradiente de altura,
\
e o segundo em termos do gradiente de pressão,
\
Assim, \(\frac{dh}{dx}\) é chamado o cabeça hidráulica porque a origem física do termo na Lei de Darcy é o gradiente de pressão no fluido, que conduz o fluxo.
água deixando um aquífero
vamos agora fazer um exemplo calculando a velocidade fluida da água entrando em um aquífero. No esboço abaixo da altura do aquífero segue-se a topografia na colina adjacente ao vale com o riacho. A água flui de alta pressão (altura da cabeça) para o vale e deixa o aquífero na corrente. Podemos usar a lei da Darcy para estimar a taxa de fluxo de água do aquífero.
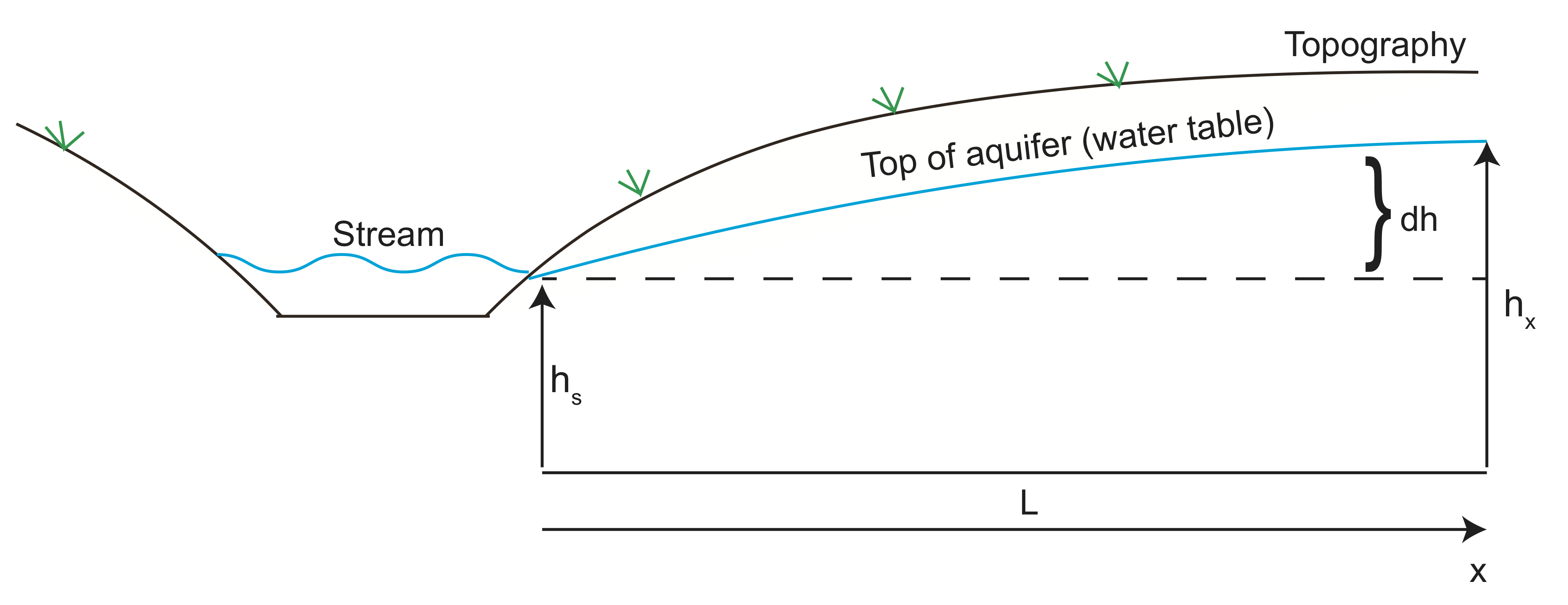
Usando imagens geofísicas, a altura do aquífero encontra-se a 10 m (\(dh\)) acima da altura da corrente a cerca de 100 metros (\(L\)) de distância. Assuma que a condutividade hidráulica é \ (K=10^{-6}\) m/s e a porosidade é \(\varphi=30\)%.
O darcy, o fluxo
\
\
\
A velocidade do fluido é
\
\
\
\

Laminar versus Fluxo Turbulento
Uma das suposições implícitas na lei de Darcy é que o fluxo é laminar. O fluxo Laminar é caracterizado como consistindo de camadas finas ou lâminas de fluido que se movem paralelamente um ao outro. Em contraste, o fluxo turbulento é caracterizado por rodopios, vórtices e eddies, em que camadas adjacentes de fluido divergem e tomam diferentes caminhos para baixo fluxo.uma maneira que podemos quantificar se um fluido é laminar ou turbulento é calculando o número do Reynold para o fluxo, definido como
\
O número do Reynold é encontrado considerando os dois termos no balanço de momento para o fluxo. O primeiro termo é a força inercial por volume de unidade, que impulsiona o fluxo, \(\rho u\frac{du}{dx}\). O segundo termo é a força viscosa por unidade de volume, que resiste ao fluxo, \(\eta\frac{d^2u}{dx^2}\). Estes dois termos devem Balancear, para que possamos defini-los iguais,
\
a seguir, reescrevemos os Termos, de uma forma simplificada para capturar apenas as dimensões relevantes das variáveis. Para fazer, passamos pelo que se chama uma análise dimensional, na qual substituímos cada variável, por valores de referência, vezes uma forma não-dimensional da variável.
Por exemplo, para o termo \(x\) é reescrito como apenas \(L x’\), onde \(L\) é o comprimento de referência (a profundidade do fluido) e \(x’\) é a distância não-dimensional. Da mesma forma, deixamos \(u = u_o u’\). Substituindo estes na equação, obtemos
\
em seguida, combinar os valores constantes na frente
\
Note que a combinação de variáveis em frente é Reynold é o número
\
, onde as variáveis são \(u_o\) velocidade de vazão, L de fluido de profundidade, e as variáveis que vimos anteriormente, \(\rho\) densidade do fluido, e \(\eta\) viscosidade do fluido. Ao passar por esta análise, descobrimos que qualquer fluxo que se caracteriza pelo equilíbrio destes dois termos pode ser comparado simplesmente conhecendo o valor do número de Reynolds. Por exemplo, se um fluxo tem uma viscosidade que é 10 vezes a viscosidade em outro fluxo, os dois fluxos se comportará da mesma é a densidade (ou de velocidade ou duração) também é aumentada por um fator de 10 para a maior viscosidade do caso; isto é, o número de Reynolds para os dois fluxos é o mesmo.para ter Darcy flow, o número de Reynold deve ser inferior a 1-10 (laminar). Para \(Re>1-10 \) o fluxo não é estritamente laminar, mas ainda não é turbulento (não-linear, não-laminar). Para ter um fluxo turbulento, o número do Reynold deve ser superior a cerca de 2000.
entendendo que as constantes no numerador e denominador afetam as características do fluxo da maneira oposta, também ajudam a pensar sobre como diferentes fluidos se comportarão em condições externas semelhantes. Por exemplo, um fluido mais denso que também tem uma velocidade rápida terá um Re maior e exibirá um comportamento turbulento. Em contraste, um fluido como o gelo que tem uma viscosidade elevada e se move muito lentamente terá um Re baixo e provavelmente terá fluxo laminar. A alta viscosidade do gelo atua para estabilizar o fluxo. Como outro exemplo, considere que dois fluidos podem estar se movendo à mesma velocidade se comportam de forma diferente se os outros valores no número \do Reynold (\frac{\rho L} {\mu}\) são diferentes. Portanto, o tipo de fluxo depende não apenas da velocidade do fluxo, mas da combinação de variáveis no número do Reynold.
a aplicação do fluxo de Darcy
a lei de Darcy é a principal equação que rege o fluxo em aquíferos e poços. Sem ela, não seríamos capazes de perfurar poços ou entender o movimento da água em aquíferos, especialmente no Vale Central da Califórnia, onde ambas as ideias são cruciais tanto para a produtividade agrícola como para a subsidência das águas subterrâneas.
