regresja do średniej jest powszechnym zjawiskiem statystycznym, które może wprowadzić nas w błąd, gdy obserwujemy świat. Uczenie się rozpoznawania, kiedy regresja do średniej jest w grze, może pomóc nam uniknąć błędnej interpretacji danych i zobaczenia wzorców, które nie istnieją.

***

ważne jest, aby zminimalizować przypadki złego osądu i rozwiązać słabe punkty w naszym rozumowaniu. Nauka o regresji do średniej może nam pomóc.

uhonorowany Nagrodą Nobla psycholog Daniel Kahneman napisał książkę o uprzedzeniach, które zaciemniają nasze rozumowanie i zniekształcają nasze postrzeganie rzeczywistości. Okazuje się, że popełniamy cały zestaw błędów logicznych, ponieważ nasza intuicja i mózg nie radzą sobie dobrze z prostymi statystykami. Jednym z błędów, które bada w szybkim i wolnym myśleniu, jest niesławna regresja w kierunku średniej.

pojęcie regresji do średniej opracował po raz pierwszy Sir Francis Galton. Zasada mówi, że w każdej serii ze złożonymi zjawiskami zależnymi od wielu zmiennych, w której bierze udział przypadek, ekstremalne wyniki zwykle następują po bardziej umiarkowanych.

w poszukiwaniu mądrości Peter Bevelin podaje przykład Johna, który był niezadowolony z wyników nowych pracowników, więc umieścił ich w programie zwiększającym umiejętności, w którym mierzył umiejętności pracowników:

ich wyniki są teraz wyższe niż w pierwszym teście. Wniosek Johna: „program zwiększający umiejętności spowodował poprawę umiejętności.”To niekoniecznie prawda. Ich wyższe wyniki mogą być wynikiem regresji do średniej. Ponieważ osoby te były mierzone jako znajdujące się na niskim końcu skali umiejętności, wykazałyby poprawę, nawet gdyby nie skorzystały z programu zwiększającego umiejętności. A może być wiele powodów ich wcześniejszego działania-stres, zmęczenie, choroba, rozproszenie uwagi itp. Ich prawdziwa zdolność może się nie zmieniła.

nasza wydajność zawsze waha się wokół pewnej średniej prawdziwej wydajności. Ekstremalne osiągi stają się mniej ekstremalne następnym razem. Dlaczego? Pomiary testowe nigdy nie mogą być dokładne. Wszystkie pomiary składają się z jednej części rzeczywistej i jednej części błędu losowego. Gdy pomiary są ekstremalne, mogą być częściowo spowodowane przez przypadek. Przy drugim mierzeniu wydajności szansa prawdopodobnie wniesie mniejszy wkład.

Jeśli przechodzimy z jednego sposobu robienia czegoś na inny tylko dlatego, że nam się nie udaje, jest bardzo prawdopodobne, że następnym razem radzimy sobie lepiej, nawet jeśli nowy sposób robienia czegoś jest równy lub gorszy.

jest to jeden z powodów, dla których niebezpieczne jest ekstrapolowanie na podstawie małych rozmiarów próbek, ponieważ dane mogą nie być reprezentatywne dla dystrybucji. Dlatego też James March twierdzi, że im dłużej ktoś pozostaje w swojej pracy, „tym mniejsza jest prawdopodobna różnica między obserwowanym zapisem wydajności a rzeczywistymi zdolnościami.”Wszystko może się zdarzyć w krótkim czasie, zwłaszcza w każdym wysiłku, który wymaga połączenia umiejętności i szczęścia. (Stosunek umiejętności do szczęścia wpływa również na regresję do średniej.)

regresja do średniej

skutki regresji do średniej można często zaobserwować w sporcie, gdzie efekt powoduje wiele nieuzasadnionych spekulacji.

myśląc szybko i powoli, Kahneman przypomina sobie oglądanie skoków narciarskich mężczyzn, dyscypliny, w której końcowy wynik jest połączeniem dwóch oddzielnych skoków. Świadomy regresji do średniej, Kahneman był zaskoczony, słysząc prognozy komentatora dotyczące drugiego skoku. Pisze::

Norwegia miała świetny pierwszy skok; będzie spięty, mając nadzieję, że obroni prowadzenie i prawdopodobnie zrobi gorzej” lub „Szwecja miała zły pierwszy skok i teraz wie, że nie ma nic do stracenia i będzie zrelaksowany, co powinno mu pomóc zrobić lepiej.

Kahneman zwraca uwagę, że komentator zauważył regresję do średniej i wymyślił historię, dla której nie było dowodów przyczynowych (patrz błąd narracyjny). Nie oznacza to, że jego historia nie może być prawdziwa. Być może, gdybyśmy zmierzyli tętno przed każdym skokiem, zobaczylibyśmy, że są bardziej zrelaksowani, jeśli pierwszy skok był zły. Jednak nie o to chodzi. Chodzi o to, że regresja do średniej ma miejsce, gdy szczęście odgrywa rolę, tak jak miało to miejsce w wyniku pierwszego skoku.

lekcja ze sportu dotyczy każdej aktywności, w której los odgrywa rolę. Często dołączamy wyjaśnienia naszego wpływu na dany proces do postępu lub jego braku.

w rzeczywistości nauka o wydajności jest złożona, zależna od sytuacji i często wiele z tego, co myślimy, że jest pod naszą kontrolą, jest naprawdę przypadkowe.

w przypadku skoków narciarskich Silny Wiatr w stosunku do skoczka doprowadzi nawet do tego, że nawet najlepszy zawodnik osiągnie przeciętne wyniki. Podobnie silny wiatr i warunki narciarskie na korzyść przeciętnego skoczka mogą prowadzić do znacznego, ale chwilowego przeskoku w jego wynikach. Efekty te jednak znikną, gdy Warunki się zmienią, a wyniki powrócą do normy.

może to mieć poważne konsekwencje dla coachingu i śledzenia wyników. Zasady regresji sugerują, że oceniając wydajność lub zatrudnienie, musimy polegać bardziej na wynikach niż na wynikach konkretnych sytuacji. W przeciwnym razie jesteśmy skłonni do rozczarowania.

Kiedy Kahneman wygłaszał wykład dla Izraelskich Sił Powietrznych na temat psychologii skutecznego szkolenia, jeden z oficerów podzielił się swoim doświadczeniem, że wysławianie podwładnych prowadzi do gorszych wyników, podczas gdy karcenie prowadzi do poprawy w późniejszych wysiłkach. W rezultacie stał się hojny z negatywnymi opiniami i stał się raczej ostrożny w udzielaniu zbyt wielu pochwał.

Kahneman natychmiast zauważył, że jest to regresja do średniej w pracy. Zilustrował błędne przekonanie prostym ćwiczeniem, które możesz wypróbować. Narysował okrąg na tablicy, a następnie poprosił oficerów, jeden po drugim, aby rzucili kawałek kredy na środek koła plecami do tablicy. Następnie powtórzył eksperyment i zapisał wyniki każdego oficera w pierwszej i drugiej próbie.

naturalnie, ci, którzy radzili sobie niesamowicie dobrze przy pierwszej próbie, Zwykle radzili sobie gorzej przy drugiej próbie i odwrotnie. Błąd natychmiast stał się jasny: zmiana wydajności występuje naturalnie. To znowu nie znaczy, że sprzężenie zwrotne w ogóle nie ma znaczenia-może tak, ale oficer nie miał dowodów, aby stwierdzić, że tak.

niedoskonała korelacja i przypadek

w tym momencie możesz się zastanawiać, dlaczego regresja do średniej ma miejsce i jak możemy upewnić się, że jesteśmy tego świadomi, gdy to nastąpi.

aby zrozumieć regresję do średniej, musimy najpierw zrozumieć korelację.

współczynnik korelacji między dwoma miarami, który waha się między -1 a 1, jest miarą względnej wagi dzielonych przez nie czynników. Na przykład dwa zjawiska z kilkoma wspólnymi czynnikami, takie jak spożycie wody butelkowanej a wskaźnik samobójstw, powinny mieć współczynnik korelacji bliski 0. Oznacza to, że gdybyśmy przyjrzeli się wszystkim krajom na świecie i wykreślili wskaźnik samobójstw w danym roku w stosunku do spożycia wody butelkowanej na mieszkańca, Wykres nie wykazałby żadnego wzorca.

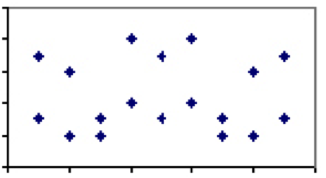
przeciwnie, istnieją środki, które są zależne wyłącznie od tego samego czynnika. Dobrym przykładem jest temperatura. Jedyny czynnik określający temperaturę-prędkość cząsteczek-jest dzielony przez wszystkie skale, stąd każdy stopień w stopniach Celsjusza będzie miał dokładnie jedną odpowiadającą mu wartość w Fahrenheicie. Dlatego temperatura w stopniach Celsjusza i Fahrenheita będzie miała współczynnik korelacji 1, A wykres będzie linią prostą.

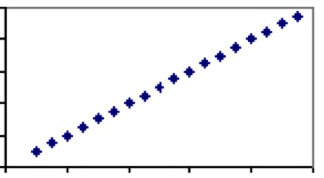
w naukach humanistycznych istnieje kilka zjawisk, jeśli w ogóle występują, które mają współczynnik korelacji 1. Istnieje jednak wiele przypadków, w których związek jest słaby do umiarkowanego i istnieje pewna siła wyjaśniająca między tymi dwoma zjawiskami. Rozważmy korelację między wysokością i wagą, która wylądowałaby gdzieś pomiędzy 0 a 1. Podczas gdy praktycznie każdy trzylatek będzie lżejszy i krótszy niż każdy dorosły mężczyzna, nie wszyscy dorośli mężczyźni lub trzylatki tego samego wzrostu będą ważyć tyle samo.

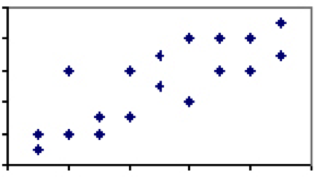
ta zmienność i odpowiadający jej niższy stopień korelacji oznacza, że chociaż wzrost jest ogólnie rzecz biorąc dobrym wskaźnikiem, wyraźnie istnieją czynniki inne niż wzrost. Kiedy korelacja dwóch miar jest mniejsza niż doskonała, musimy uważać na skutki regresji do średniej.

Kahneman przestrzega ogólnej zasady: ilekroć korelacja między dwoma Wynikami jest niedoskonała, następuje regresja do średniej.

to na początku może wydawać się mylące i niezbyt intuicyjne, ale stopień regresji do średniej jest bezpośrednio związany ze stopniem korelacji zmiennych. Efekt ten można zilustrować prostym przykładem.

Załóżmy, że jesteś na imprezie i zapytaj, dlaczego wysoce inteligentne kobiety mają tendencję do poślubienia mężczyzn, którzy są mniej inteligentni niż oni. Większość ludzi, nawet tych z pewnym wyszkoleniem w statystykach, szybko wskoczy do różnych przyczynowych wyjaśnień, począwszy od unikania konkurencji po lęki przed samotnością, z którymi borykają się te kobiety. Temat takich kontrowersji może wywołać wielką debatę.

a co jeśli zapytamy, dlaczego korelacja między wynikami inteligencji małżonków jest mniejsza niż doskonała? To pytanie nie jest tak interesujące i nie ma co zgadywać – wszyscy wiemy, że to prawda. Paradoks polega na tym, że te dwa pytania są algebraicznie równoważne. Kahneman wyjaśnia:

Jeśli korelacja między inteligencją małżonków jest mniejsza niż doskonała (i jeśli mężczyźni i kobiety średnio nie różnią się inteligencją), to matematyczną nieuchronnością jest, że wysoce inteligentne kobiety będą poślubiać mężów, którzy są średnio mniej inteligentni niż oni (i odwrotnie, oczywiście). Obserwowana regresja do średniej nie może być bardziej interesująca lub bardziej wyjaśnialna niż korelacja niedoskonała.

zakładając, że korelacja jest niedoskonała, szanse dwóch partnerów reprezentujących górny 1% pod względem jakiejkolwiek cechy są znacznie mniejsze niż jeden partner reprezentujący górny 1%, a drugi – dolny 99%.

przyczyna, skutek i leczenie

powinniśmy być szczególnie ostrożni z regresją do zjawiska średniej, próbując ustalić związek przyczynowy między dwoma czynnikami. Ilekroć korelacja jest niedoskonała, Najlepsze zawsze wydają się pogarszać, a najgorsze wydają się z czasem poprawiać, niezależnie od dodatkowego leczenia. Jest to coś, czego ogólne media, a czasem nawet wyszkoleni naukowcy, nie potrafią rozpoznać.

rozważ przykład, który podaje Kahneman:

dzieci z depresją leczonych napojem energetycznym znacznie poprawiają się w okresie trzech miesięcy. Wymyśliłem ten nagłówek gazety, ale fakt, że donosi, jest prawdą: jeśli przez jakiś czas leczysz grupę dzieci z depresją napojem energetycznym, wykazałyby one klinicznie istotną poprawę. Zdarza się również, że depresyjne dzieci, które spędzają trochę czasu stojąc na głowie lub przytulając kota przez dwadzieścia minut dziennie, również wykazują poprawę.

za każdym razem, gdy natkniesz się na takie nagłówki, bardzo kuszące jest wyciągnięcie wniosku, że napoje energetyczne, stanie na głowie lub przytulanie kotów są doskonale realnymi lekarstwami na depresję. Te przypadki, jednak po raz kolejny ucieleśniają regresję do średniej:

dzieci z depresją są grupą skrajną, są bardziej przygnębione niż większość innych dzieci—a grupy skrajne z czasem regresują do średniej. Korelacja między wynikami depresji przy kolejnych testach jest mniejsza niż idealna, więc nastąpi regresja do średniej: dzieci z depresją będą nieco lepsze z czasem, nawet jeśli nie będą przytulać kotów i nie będą pić Red Bulla.

często błędnie przypisujemy określoną politykę lub leczenie jako przyczynę skutku, gdy zmiana w skrajnych grupach i tak by się wydarzyła. Stanowi to fundamentalny problem: skąd możemy wiedzieć, czy efekty są rzeczywiste, czy po prostu spowodowane zmiennością?

na szczęście istnieje sposób, aby odróżnić prawdziwą poprawę od regresji do średniej. Jest to wprowadzenie tak zwanej grupy kontrolnej, która ma się poprawić poprzez samą regresję. Celem badań jest ustalenie, czy badana grupa poprawia się bardziej niż regresja może wyjaśnić.

w rzeczywistych sytuacjach z wynikami konkretnych osób lub zespołów, gdzie jedynym prawdziwym punktem odniesienia jest przeszła wydajność i nie można wprowadzić grupy kontrolnej, skutki regresji mogą być trudne, jeśli nie niemożliwe do rozwikłania. Możemy porównać ze średnią branżową, rówieśnikami w grupie kohortowej lub historycznymi wskaźnikami poprawy, ale żaden z nich nie jest doskonałym miernikiem.

***

na szczęście świadomość regresji do samego zjawiska średniej jest już świetnym pierwszym krokiem w kierunku bardziej ostrożnego podejścia do zrozumienia szczęścia i wydajności.

Jeśli jest coś, czego można się nauczyć od regresji do średniej, to znaczenie rekordów osiągnięć, a nie polegania na jednorazowych historiach sukcesu. Mam nadzieję, że następnym razem, gdy natkniesz się na ekstremalną jakość częściowo rządzoną przez przypadek, zdasz sobie sprawę, że efekty mogą się z czasem cofać i odpowiednio dostosujesz swoje oczekiwania.

co dalej czytać

• Ulepsz swoje myślenie dzięki 113 modelom mentalnym.
• przeczytaj o myśleniu drugiego poziomu, aby uniknąć negatywnych konsekwencji.