Nota wydawcy

poniższy raport z badań studenckich został przygotowany dla klasy profesor Judit Kardos Math 255, która odbyła się w College of New Jersey. Był to 3-kredytowy kurs wprowadzający w historii matematyki. Raport ten był liczony do 30% końcowej oceny. Jest to przykład tego rodzaju badań historycznych studenci mogą zrobić przy użyciu źródeł wtórnych.

rozwiązanie problemu mostu Königsberg przez Leonarda Eulera

Königsberg

nasza historia zaczyna się w XVIII wieku, w uroczym mieście Königsberg, w Prusach, nad brzegiem rzeki Pregel. W 1254 roku Krzyżacy założyli miasto Królewiec pod wodzą czeskiego króla Ottokara II po drugiej krucjacie przeciwko Prusom. W średniowieczu Königsberg stał się bardzo ważnym miastem i centrum handlowym z jego strategicznym położeniem nad rzeką. Grafika z XVIII wieku pokazuje Königsberg jako prężnie rozwijające się miasto, w którym floty statków wypełniają Pregel, a ich handel oferuje komfortowy styl życia zarówno lokalnym kupcom, jak i ich rodzinom. Zdrowa gospodarka pozwoliła mieszkańcom miasta zbudować siedem mostów przez rzekę, z których większość łączyła się z wyspą Kneiphof; ich lokalizacje można zobaczyć na załączonym zdjęciu .

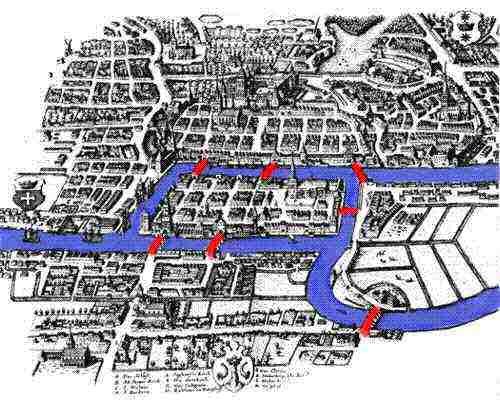
gdy rzeka płynęła wokół Kneiphof, dosłownie oznaczając pub yard, i inną wyspę, podzieliła miasto na cztery odrębne regiony. Siedem mostów nazwano mostem Kowala, mostem łącznikowym, mostem Zielonym, mostem kupieckim, mostem drewnianym, mostem wysokim i Mostem miodowym. Według legendy, mieszkańcy Królewca spędzali niedzielne popołudnia spacerując po swoim pięknym mieście. Podczas spaceru mieszkańcy miasta postanowili stworzyć grę dla siebie, a ich celem było wymyślenie sposobu, w jaki mogliby chodzić po mieście, przekraczając każdy z siedmiu mostów tylko raz. Chociaż żaden z mieszkańców Królewca nie mógł wymyślić trasy, która pozwoliłaby im przekroczyć każdy z mostów tylko raz, nie mogli udowodnić, że jest to niemożliwe. Na szczęście Königsberg nie był zbyt daleko od Petersburga, domu słynnego matematyka Leonarda Eulera.

Euler i Problem mostu

Dlaczego Euler miałby zajmować się problemem tak niezwiązanym z dziedziną matematyki? Dlaczego tak wielki matematyk miałby spędzać dużo czasu z trywialnym problemem, takim jak problem mostu królewieckiego? Euler był oczywiście zajętym człowiekiem, wydając w ciągu swojego życia ponad 500 książek i referatów. Tylko w 1775 roku napisał średnio jedną pracę matematyczną tygodniowo, a za życia pisał na różne tematy oprócz matematyki, w tym mechanikę, optykę, astronomię, nawigację i hydrodynamikę. Nic dziwnego, że Euler uznał ten problem za trywialny, stwierdzając w liście z 1736 roku do Carla Leonharda Gottlieba Ehlera, burmistrza Gdańska, który poprosił go o rozwiązanie tego problemu :

. . . Tak więc widzi pan, najszlachetniejszy panie, jak ten rodzaj rozwiązania ma niewielki związek z matematyką i nie rozumiem, dlaczego oczekuje Pan, że matematyk go stworzy, a nie ktokolwiek inny, ponieważ rozwiązanie opiera się wyłącznie na rozumowaniu, a jego odkrycie nie zależy od żadnej matematycznej Zasady. Z tego powodu nie wiem dlaczego nawet pytania, które mają tak mały związek z matematyką, są rozwiązywane szybciej przez matematyków niż przez innych.

mimo, że Euler uznał problem za trywialny, nadal był nim zaintrygowany. W liście napisanym w tym samym roku do Giovanniego Marinoniego, włoskiego matematyka i inżyniera, Euler powiedział:

to pytanie jest tak banalne, ale wydawało mi się godne uwagi w tym, że geometria, ani algebra, ani nawet sztuka liczenia nie były wystarczające, aby je rozwiązać.

Euler uważał, że ten problem jest związany z tematem, który Gottfried Wilhelm Leibniz kiedyś omawiał i chciał nad nim pracować, czymś, co Leibniz określał jako geometria situs, czyli geometria położenia. Ta tak zwana geometria położenia jest tym, co obecnie nazywa się teorią grafów, którą Euler wprowadza i wykorzystuje przy rozwiązywaniu tego słynnego problemu.

dowód Eulera

26 sierpnia 1735 roku Euler przedstawia pracę zawierającą rozwiązanie problemu mostu królewieckiego. Zajmuje się zarówno tym specyficznym problemem, jak i ogólnym rozwiązaniem z dowolną liczbą mas lądowych i dowolną liczbą mostów. Praca ta, zatytułowana „Solutio problematis ad geometriam situs pertinentis”, została później opublikowana w 1741 roku . Artykuł Eulera podzielony jest na dwadzieścia jeden ponumerowanych akapitów, a w dalszej części zostanie przedstawiona uproszczona wersja akapitów Eulera.

w dwóch pierwszych akapitach dowodu Eulera wprowadza problem mostu królewieckiego. W ust. 1 Euler stwierdza, że jego zdaniem problem ten dotyczy geometrii, ale nie geometrii dobrze znanej jego rówieśnikom, która obejmuje pomiary i obliczenia, ale nowego rodzaju geometrii, którą Leibniz nazwał geometrią położenia. Następnie w ust. 2 Euler wyjaśnia swoim słuchaczom, jak działa problem Królewiec. Euler przedstawił szkic problemu (patrz rysunek Eulera 1) i nazwał siedem różnych mostów: a, b, c, d, e, f I, g. w tym akapicie stwierdza ogólne Pytanie problemu: „czy można dowiedzieć się, czy można przekroczyć każdy most dokładnie raz?”

rysunek Eulera 1 z 'Solutio problematis ad geometriam situs pertinentis,’ Eneström 53

po określeniu ogólnego pytania, które próbuje rozwiązać, Euler zaczyna badać różne metody znalezienia rozwiązania. W ustępie 3 Euler mówi czytelnikowi, że aby rozwiązać ten konkretny problem, mógłby zapisać wszystkie możliwe ścieżki, ale ta technika zajęłaby dużo czasu i nie działałaby w większych konfiguracjach z większą liczbą mostów i mas lądowych. Z powodu tych problemów Euler postanowił wybrać inną metodę rozwiązania tego problemu.

w ust. 4 zaczyna upraszczać problem wymyślając wygodny system do reprezentowania przejścia przez most. Euler zdecydował, że zamiast używać małych liter do reprezentowania przejścia przez most, napisze wielkie litery reprezentujące obszary lądowe. Na przykład, odwołując się do jego rysunku 1, AB oznaczałoby podróż, która rozpoczęła się w przejściu a, a zakończyła na B. Ponadto, jeśli po podróży z przejścia a do B, ktoś zdecyduje się przejść do przejścia D, byłoby to po prostu oznaczone, ABD. W ustępie 5 Euler kontynuuje dyskusję na ten temat, wyjaśniając, że w ABDC, choć istnieją cztery duże litery, tylko trzy mosty zostały skrzyżowane. Euler wyjaśnia, że bez względu na to, ile jest mostów, będzie jeszcze jedna litera reprezentująca konieczne przejście. Z tego powodu cały problem mostu Königsberg wymagał przekroczenia siedmiu mostów, a zatem ośmiu wielkich liter.

w punkcie 6 Euler kontynuuje objaśnianie szczegółów swojej metody. Mówi czytelnikowi, że jeśli istnieje więcej niż jeden most, który można przekroczyć, przechodząc z jednego przejścia do drugiego, nie ma znaczenia, który most jest używany. Na przykład, nawet jeśli istnieją dwa mosty, a i b, które mogą zabrać podróżnego z A do B, nie ma znaczenia w notacji Eulera, który most zostanie przejęty. W tym punkcie Euler omawia również konkretny problem, z którym ma do czynienia. Wyjaśnia, wykorzystując swoją oryginalną figurę, że problem Königsberga potrzebuje dokładnie ośmiu liter, gdzie pary (A, B) I (A, C) muszą pojawić się obok siebie dokładnie dwa razy, bez względu na to, która litera pojawia się pierwsza. Ponadto pary (A,D), (B,D) i (C, D) muszą wystąpić razem dokładnie raz,aby ścieżka, która przecina każdy most raz i tylko raz, istniała.

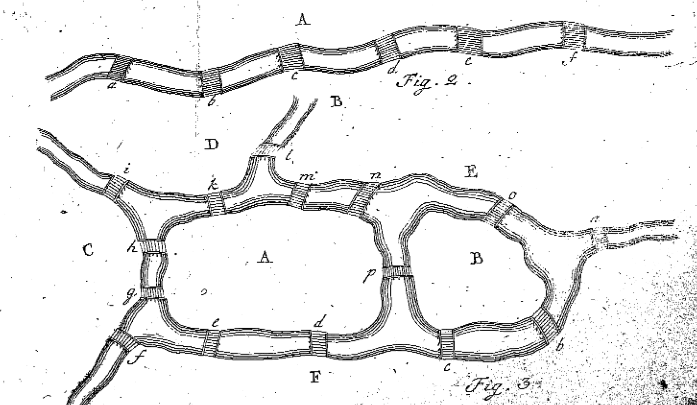
figury Eulera 2 i 3 z „Solutio problematis ad geometriam situs pertinentis,” Eneström 53

w paragrafie 7 Euler informuje czytelnika, że albo musi znaleźć ośmioliterową sekwencję, która zaspokoi problem, albo musi udowodnić, że taka sekwencja nie istnieje. Zanim zrobi to dla problemu mostu Königsberg, postanawia znaleźć regułę, aby odkryć, czy istnieje ścieżka dla bardziej ogólnego problemu. Czyni to w ustępie 8, patrząc na znacznie prostszy przykład mostów i mostów. Euler rysuje Rysunek 2 i zaczyna oceniać sytuacje, przez które przemierza się region A. Euler twierdzi, że jeśli most a został przejechany raz, to A było miejscem rozpoczęcia lub zakończenia podróży i dlatego był używany tylko raz. Jeśli mosty a, b i c są przejechane raz, A jest używane dokładnie dwa razy, bez względu na to, czy jest to miejsce początkowe, czy końcowe. Podobnie, jeśli pięć mostów prowadzi do A, to w trakcie podróży lądowisko A wystąpiłoby dokładnie trzy razy. Euler stwierdza, że ” ogólnie rzecz biorąc, jeśli liczba mostów jest dowolną liczbą nieparzystą i jeśli jest zwiększona o jeden, to liczba wystąpień a jest połową wyniku.”Innymi słowy, jeśli istnieje Nieparzysta liczba mostów łączących A z innymi lądami, dodaj jeden do liczby mostów i podziel ją przez dwa, aby dowiedzieć się, ile razy należy użyć a na ścieżce, gdzie każdy most jest używany raz i tylko raz (tj. Wszystkie wystąpienia A, gdzie A ma nieparzyste # mostów = (#mostów-1) / 2).

korzystając z tego faktu Euler rozwiązuje problem mostu Königsberg w pkt 9. W takim przypadku, ponieważ istnieje pięć mostów, które prowadzą do A, musi wystąpić trzy razy (patrz jego rysunek 1, powyżej). Podobnie B, C i D muszą pojawić się dwa razy, ponieważ wszystkie mają trzy mosty, które do nich prowadzą. Dlatego 3(Dla a) + 2(dla B) + 2(dla C) + 2 (dla D) = 9, ale Euler stwierdził już, że musi być tylko osiem wystąpień dla siedmiu mostów. To jest sprzeczność! Dlatego nie można podróżować mostami w mieście Königsberg raz i tylko raz. Koniec, czy już? Chociaż mieszkańcy Królewca mogą być zadowoleni z tego rozwiązania, wielki matematyk Leonhard Euler nie był zadowolony. Euler kontynuuje swój dowód, aby radzić sobie z bardziej ogólnymi sytuacjami.

uogólnienie Eulera

w ustępie 10 Euler kontynuuje swoją dyskusję, zauważając, że jeśli sytuacja dotyczy wszystkich lądowisk o nieparzystej liczbie mostów, można stwierdzić, czy podróż może być wykonana przy użyciu każdego mostu tylko raz. Euler stwierdza, że jeśli suma liczby razy każda litera musi się pojawić jest o jeden więcej niż całkowita liczba mostów, można wykonać podróż. Jeśli jednak liczba wystąpień jest większa niż o jeden więcej niż liczba mostów, nie można wykonać podróży, jak w przypadku problemu mostu Königsberg. Dzieje się tak dlatego, że reguła, którą daje Euler dla nieparzystej liczby mostów, używając swojej liczby 2, jest prawdziwa dla ogólnej sytuacji, czy istnieje tylko jeden inny ląd, czy więcej niż jeden.

w paragrafach 11 i 12 Euler zajmuje się sytuacją, w której dany region posiada parzystą liczbę mostów. Sytuacja ta nie pojawia się w problemie Königsberga i dlatego była ignorowana do dziś. W sytuacji, gdy landmass X ma parzystą liczbę mostów, mogą wystąpić dwa przypadki. Pierwszy przypadek dotyczy sytuacji, gdy X jest punktem wyjścia do podróży. W tym przypadku X pojawi się dwa razy, raz jako punkt początkowy i ponownie jako punkt końcowy. W drugim przypadku X nie jest punktem wyjścia. Gdyby tak się stało, x pojawiłby się tylko raz, ponieważ podróż musiałaby wejść przez jeden most i natychmiast opuścić jedyny dostępny most. Podobnie, jeśli istnieją cztery mosty przymocowane do X, liczba wystąpień x zależy od tego, czy jest to punkt początkowy. Jeśli podróż zaczyna się w X, musi pojawić się trzy razy, ale jeśli nie rozpocznie się w X, pojawi się tylko dwa razy. Tak więc ogólnie, jeśli X ma parzystą liczbę mostów dołączonych, to jeśli podróż nie rozpoczyna się w X, X pojawia się o połowę więcej niż liczba razy jako mosty (tj. Wystąpienia X, gdzie X jest parzyste, a nie punkt wyjścia = (# mostów) / 2). Jeśli podróż zaczyna się w X, to X pojawia się w połowie liczby razy jako mosty, plus jeden (tj. wystąpienia X, gdzie X jest parzyste i punkt początkowy = ((#mostów) / 2) + 1).

w paragrafach 13-15 Euler wyjaśnia, jak ustalić, czy istnieje ścieżka korzystająca z każdego mostu raz i tylko raz, i przedstawia swój własny przykład, aby pokazać, jak to działa. Euler najpierw wyjaśnia swoją prostą, sześciostopniową metodę rozwiązywania wszelkich ogólnych sytuacji z lądami podzielonymi przez rzeki i połączonymi mostami. Pierwszy Euler oznacza każdy teren wielką literą. Po drugie, bierze całkowitą liczbę mostów, dodaje jeden i pisze To nad wykresem, który ma zamiar zrobić. Następnie bierze wielkie litery, umieszcza je w kolumnie, a obok nich pisze liczbę mostów. Po czwarte, wskazuje gwiazdkami lądowiska, które mają parzystą liczbę mostów. Następnie, obok każdej parzystej liczby, zapisuje ½ liczby, a obok każdej nieparzystej liczby umieszcza ½ liczby plus jeden. Wreszcie, Euler dodaje liczby zapisane w prawej kolumnie i jeśli suma jest o jeden mniejsza lub równa liczbie mostów plus jeden, to wymagana podróż jest możliwa. Ważne jest jednak, aby pamiętać, że jeśli suma jest o jeden mniej niż liczba mostów plus jeden, to podróż musi rozpocząć się od jednego z lądów oznaczonych gwiazdką. Jeśli suma jest równa liczbie mostów plus jeden, podróż musi rozpocząć się w regionie nie oznaczonym gwiazdką.

przykłady

używając problemu Królewca jako pierwszego przykładu Euler pokazuje następujące:

Liczba mostów = 7, Liczba mostów plus Jeden = 8

Region mosty razy Region musi się pojawić

a 5 3

B 3 2

C 3 2

D 3 2

jednak, 3 + 2 + 2 + 2 = 9, czyli więcej niż 8, więc podróż jest niemożliwa.

ponieważ ten przykład jest raczej podstawowy, Euler decyduje się zaprojektować własną sytuację z dwiema wyspami, czterema rzekami i piętnastu mostami. Sytuację stworzoną przez Eulera widać na rysunku 3 powyżej. Euler próbuje teraz ustalić, czy istnieje ścieżka, która pozwala komuś przejść przez każdy most raz i tylko raz. Euler wykonuje te same czynności, co powyżej, nazywając pięć różnych regionów wielkimi literami i tworzy tabelę, aby sprawdzić, czy jest to możliwe, na przykład:

liczba mostów = 15, liczba mostów plus jeden = 16

Region mosty razy Region powinien zostać wyświetlony

a* 8 4

B* 4 2

C* 4 2

D 3 2

E 5 3

F* 6 3

oprócz, 4 + 2 + 2 + 2 + 3 + 3 = 16, co jest równe liczbie mostów plus jeden, co oznacza, że podróż jest zasadniczo możliwa. Ponieważ suma jest równa liczbie mostów plus jeden, podróż musi rozpocząć się w D lub E. Teraz, gdy Euler wie, że możliwe jest odbycie podróży, musi tylko podać, jaka będzie ścieżka. Euler wybiera ścieżkę Eafbbcfdaefcgahcidkamenapboeld, gdzie podaje, które mosty przecinają się między literami reprezentującymi grunty. Chociaż informacje te są nieistotne, ponieważ dokładny most nie ma znaczenia, wiedząc, że podróż jest możliwa, jest to przydatne przy wyborze ścieżki. Jest to dobry przykład, który pokazuje metodę, której Euler użyłby przy rozwiązywaniu każdego problemu tego rodzaju.

wnioski Eulera

w kilku następnych akapitach Euler przedstawia inny sposób, aby dowiedzieć się, czy można odbyć podróż, biorąc pod uwagę dowolny zestaw lądów, mostów i rzek. W pkt 16 Euler wskazuje, że suma liczb wymienionych bezpośrednio na prawo od lądowisk stanowi dwukrotność całkowitej liczby mostów. Ten fakt później staje się znany jako lemat uścisku dłoni. Zasadniczo lemat uściślający stwierdza, że każdy most jest liczony dwa razy, raz dla każdego lądu, do którego jest przymocowany. W ust. 17 Euler stwierdza dalej, że suma wszystkich mostów prowadzących do każdego regionu jest parzysta, ponieważ połowa tej liczby jest równa całkowitej liczbie mostów. Jest to jednak niemożliwe, jeśli istnieje Nieparzysta liczba mostów z nieparzystą liczbą mostów. W związku z tym Euler dowodzi, że jeśli istnieją liczby nieparzyste związane z masami lądowymi, musi istnieć liczba parzysta tych mas.

jednak nie jest to wystarczające, aby udowodnić, że istnieje ścieżka, w której każdy most jest używany raz i tylko raz, ponieważ problem mostu Königsberg ma parzystą liczbę przejść z nieparzystą liczbą mostów prowadzących do nich. Z tego powodu Euler dodaje więcej ograniczeń w pkt 18 i 19. Euler wyjaśnia, że ponieważ całkowita liczba mostów przyłączonych do każdego lądu jest równa dwukrotności liczby mostów (jak widać w lemacie uściślania dłoni), więc jeśli dodasz dwa do tej sumy, a następnie podzielisz przez dwa, otrzymasz liczbę łącznych mostów plus jeden. Liczba ta jest taka sama jak poprzednio, która służy do określenia, czy ścieżka jest możliwa. Jeśli wszystkie liczby są parzyste, wtedy Trzecia kolumna w tabeli sumuje się do jednego mniej niż całkowita liczba mostów plus jeden.

Euler wyjaśnia, że jest oczywiste, że jeśli istnieją dwa lądowiska o nieparzystej liczbie mostów, podróż zawsze będzie możliwa, jeśli podróż rozpocznie się w jednym z regionów o nieparzystej liczbie mostów. Dzieje się tak, ponieważ jeśli liczby parzyste zostaną zmniejszone o połowę, a każda z nieparzystych zostanie zwiększona o jedną i zmniejszona o połowę, suma tych połówek będzie równa o jedną więcej niż całkowita liczba mostów. Jeśli jednak istnieją cztery lub więcej lądowisk z nieparzystą liczbą mostów, niemożliwe jest istnienie ścieżki. Dzieje się tak dlatego, że suma połówek liczb nieparzystych plus jeden wraz z sumą wszystkich połówek liczb parzystych sprawi, że suma trzeciej kolumny będzie większa niż całkowita liczba mostów plus jeden. W związku z tym Euler udowodnił, że mogą istnieć co najwyżej dwa lądowiska o nieparzystej liczbie mostów.

mając to na uwadze, Euler może teraz sformułować swoje wnioski dotyczące bardziej ogólnych form problemu mostu Königsberg. W paragrafie 20 Euler podaje trzy wskazówki, których można użyć, aby dowiedzieć się, czy ścieżka istnieje przy użyciu każdego mostu raz i tylko raz. Po pierwsze, twierdził, że jeśli istnieje więcej niż dwa lądowiska z nieparzystą liczbą mostów, to żadna taka podróż nie jest możliwa. Po drugie, jeśli liczba mostów jest nieparzysta dla dokładnie dwóch lądowisk, podróż jest możliwa, jeśli rozpoczyna się w jednym z dwóch nieparzystych ponumerowanych lądowisk. Wreszcie, Euler stwierdza, że jeśli nie ma regionów o nieparzystej liczbie lądów, to podróż może być zrealizowana począwszy od dowolnego regionu. Po przedstawieniu tych trzech faktów Euler kończy swój dowód ustępem 21, który po prostu stwierdza, że po ustaleniu, że ścieżka istnieje, nadal musi przejść przez wysiłek, aby napisać ścieżkę, która działa. Euler uważał, że metoda osiągnięcia tego celu jest trywialna i nie chciał poświęcać na to zbyt wiele czasu. Jednak Euler zasugerował skoncentrowanie się na tym, jak dostać się z jednego lądu do drugiego, zamiast koncentrować się na konkretnych Mostach na początku.

dowód Eulera i teoria grafów

czytając oryginalny dowód Eulera, odkrywa się stosunkowo proste i łatwo zrozumiałe dzieło matematyki; jednak to nie faktyczny dowód, ale pośrednie kroki, które czynią ten problem sławnym. Wielką innowacją Eulera było abstrakcyjne postrzeganie problemu mostu w Królewcu, poprzez wykorzystanie linii i liter do przedstawienia większej sytuacji lądowisk i mostów. Używał wielkich liter do reprezentowania lądów, a małych liter do reprezentowania mostów. Był to zupełnie nowy rodzaj myślenia na ten czas, a w swoim artykule Euler przypadkowo zapoczątkował nową gałąź matematyki zwaną teorią grafów, gdzie wykres jest po prostu zbiorem wierzchołków i krawędzi. Dziś ścieżka w grafie, która zawiera każdą krawędź grafu raz i tylko raz, nazywana jest ścieżką Euleriana, z powodu tego problemu. Od czasu rozwiązania tego problemu przez Eulera do dziś teoria grafów stała się ważną gałęzią matematyki, która kieruje podstawą naszego myślenia o sieciach.

problem z mostem Königsberg jest powodem, dla którego Biggs stwierdza,

początki teorii grafów są skromne, a nawet niepoważne … problemy, które doprowadziły do rozwoju teorii grafów, były często czymś więcej niż zagadkami, zaprojektowanymi w celu sprawdzenia pomysłowości, a nie pobudzenia wyobraźni. Jednak pomimo pozornej trywialności takich zagadek, wzbudziły one zainteresowanie matematyków, w wyniku czego teoria grafów stała się przedmiotem bogatym w wyniki teoretyczne o zaskakującej różnorodności i głębi.

jak sugeruje twierdzenie Biggsa, problem ten jest tak ważny, że jest wymieniony w pierwszym rozdziale każdej książki z teorią grafów, która była czytana w bibliotece.

po odkryciu Eulera (lub wynalazku, w zależności od tego, jak czytelnik na to patrzy) teoria grafów rozkwitła z dużym wkładem wielkich matematyków, takich jak Augustin Cauchy, William Hamilton, Arthur Cayley, Gustav Kirchhoff i George Polya. Wszyscy ci ludzie przyczynili się do odkrycia ” prawie wszystkiego, co wiadomo o dużych, ale uporządkowanych wykresach, takich jak krata utworzona przez atomy w krysztale lub sześciokątna krata wykonana przez pszczoły w ulu .”Inne znane problemy z teorią grafów obejmują znalezienie sposobu na ucieczkę z labiryntu lub labiryntu, lub znalezienie kolejności ruchów z rycerzem na szachownicy w taki sposób, że każdy kwadrat jest lądowany tylko raz, a rycerz powraca do przestrzeni, na której zaczął . Inne problemy z teorią grafów nie zostały rozwiązane od wieków .

losy Królewca

podczas gdy teoria grafów rozkwitła po tym, jak Euler rozwiązał problem mostu w Królewcu, miasto Königsberg miało znacznie inny los. W 1875 roku mieszkańcy Królewca postanowili zbudować nowy most między węzłami B I C, zwiększając liczbę połączeń tych dwóch lądowisk do czterech. Oznaczało to, że tylko dwa lądowiska miały nieparzystą liczbę linków, co dało dość proste rozwiązanie problemu. Powstanie dodatkowego mostu może, ale nie musi, być podświadomie spowodowane chęcią znalezienia drogi do rozwiązania słynnego problemu miasta.

jednak Nowy Most nie rozwiązał wszystkich przyszłych problemów Królewca, ponieważ miasto nie spodziewało się w XIX wieku „smutnego i rozdartego wojną losu, który oczekiwał go jako gospodarza jednej z najgroźniejszych bitew II wojny światowej.”W ciągu czterech dni w sierpniu 1944 roku brytyjskie bombowce zniszczyły zarówno stare miasto, jak i północną część Królewca. W styczniu i lutym 1945 roku okolice Królewca zostały otoczone przez wojska rosyjskie. Niemieccy cywile zaczynają ewakuować się z miasta, ale ruszają za późno. Tysiące ludzi ginie próbując uciec łodzią i pieszo przez lodowate wody Zalewu Kurońskiego. W kwietniu 1945 r. Armia Czerwona zdobywa Königsberg, gdzie około dziewięćdziesięciu procent starego miasta leży w ruinie.

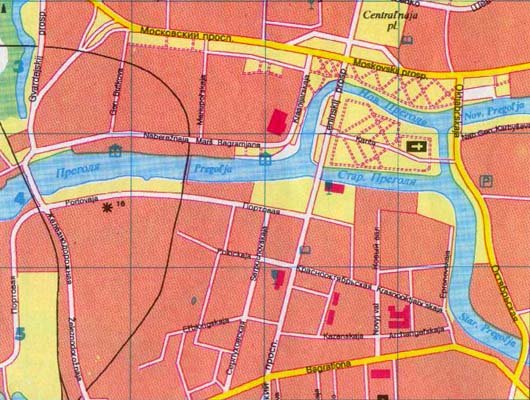
poniżej znajduje się aktualna mapa ulic Królewca . Ta mapa pokazuje, jak bardzo Miasto się zmieniło. Wiele mostów zostało zniszczonych podczas bombardowań, a miasto nie może już zadawać tego samego intrygującego pytania, które udało się w XVIII wieku. Wraz z zupełnie innym układem, miasto Königsberg ma nową nazwę, Kaliningrad, z rzeką Pregel przemianowaną na Pregolya . O ile losy Królewca są straszne, o tyle stary problem mieszkańców, polegający na przebyciu każdego ze starych siedmiu mostów dokładnie jeden raz, doprowadził do powstania zupełnie nowej gałęzi matematyki, teorii grafów.

Biggs, Norman L., E. K. Lloyd i Robin J. Wilson. Teoria Grafów: 1736-1936. Oxford: Clarendon Press, 1976.

Euler: Pan nas wszystkich. Waszyngton: The Mathematical Association of America, 1999.

Euler, Leonhard, „Solutio problematis ad geometriam situs pertinentis” (1741), Eneström 53, Maa Archiwum Eulera.

„History of Mathematics: On Leonhard Euler (1707-1783).”ScienceWeek (2003). 6 listopada 2005.

Hopkins, Brian, and Robin Wilson. „Prawda o Królewcu.”College Mathematics Journal (2004), 35, 198-207.

„mosty Królewca.”Archiwum historii matematyki MacTutor:
http://www-history.mcs.st – and.ac.uk/history/Miscellaneous/other_links/Konigsberg.html

Nota wydawcy: Ten artykuł został pierwotnie opublikowany w Convergence, Volume 3 (2006).