2.5: prawo Darcy’ ego – przepływ w Medium porowatym
prawo Darcy ’ ego jest kluczowe dla zrozumienia wielu gałęzi geologii, zwłaszcza hydrogeologii. Zanim przyjrzymy się prawu i temu, co może nam ono powiedzieć, przyjrzyjmy się, jak zostało opracowane. Prawo Darcy 'ego zostało nazwane na cześć Henry’ ego Darcy ’ ego, dziewiętnastowiecznego francuskiego inżyniera, który opracował podziemny system rur ciśnieniowych do dostarczania wody w mieście Dijon. System, który dostarczał również wodę do słynnych fontann w Dijon, zrewolucjonizował miejskie systemy wodociągowe i kanalizacyjne. System nie wymagał pomp i był napędzany wyłącznie grawitacją. Podczas opracowywania nowego systemu Darcy przeprowadził serię eksperymentów, w których próbował poruszać wodą wyłącznie za pomocą grawitacji.
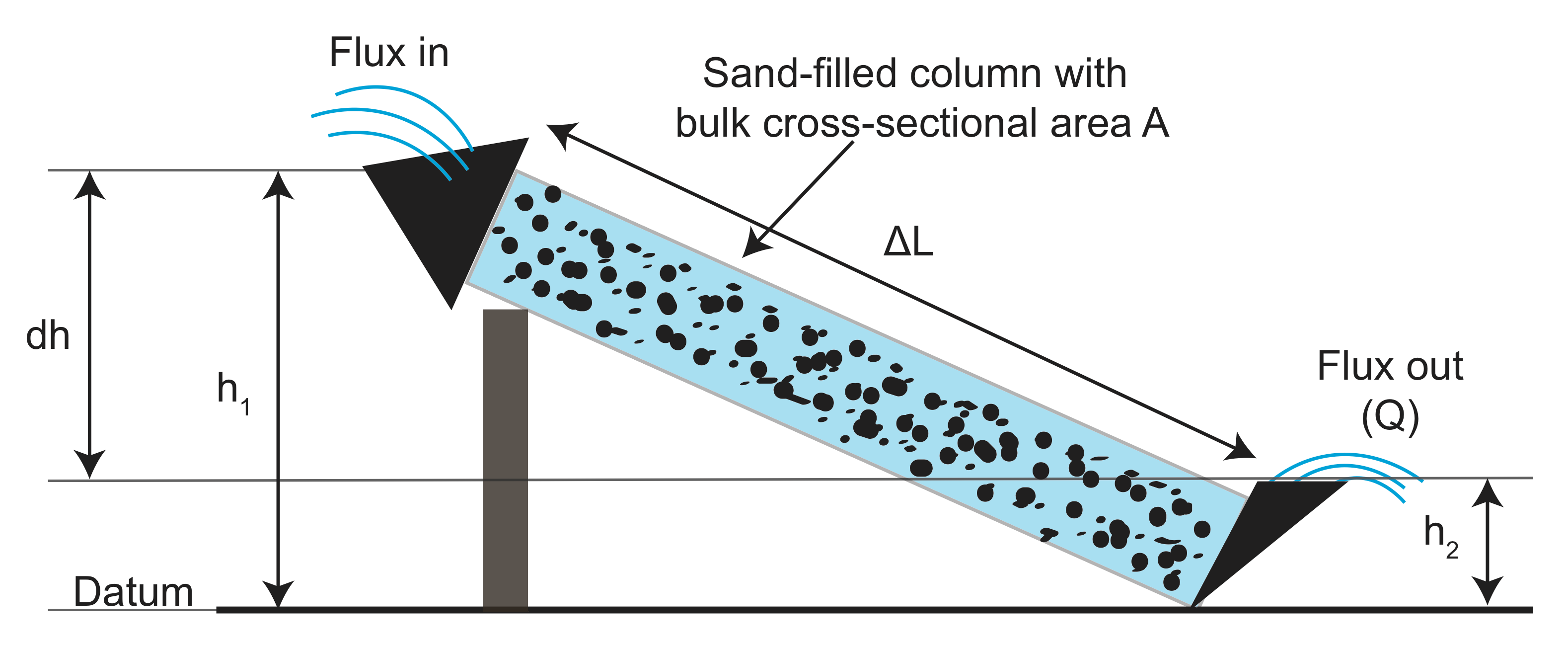
z eksperymentów, zebranych danych na temat długości flume (\(L\)), powierzchni przekroju flume (\(a\)), różnicy wysokości (\(h_1 – h_2\)) i strumienia wody wychodzącej \(Q\) zarówno z granulowanym (filtrującym) materiałem, jak i bez Flume. Następnie wykreślił pomiar strumienia znormalizowanego przez powierzchnię w stosunku do stosunku różnicy wysokości do długości strumienia (\(\frac{h_1-h_2}{l}\)). Odkrył, że istnieje zależność liniowa, a nachylenie zależy od materiału ziarnistego, którego użył w strumieniu:
\
, który można przepisać jako pochodną,
\
gdzie \(k\) to przewodność hydrauliczna, a \(\frac{Dh}{dx}\) to gradient hydrauliczny. \ (Q\), całkowita szybkość rozładowania, ma jednostki \(\frac{m^3}{s}\), objętość wody na czas. Znak ujemny wynika z faktu, że płyn przepływa w dół (ujemny) gradientu hydraulicznego od wyższych wartości do niższych wartości.
przewodność hydrauliczna jest parametrem fizycznym, który określa, jak łatwo płyn może poruszać się w przestrzeni porów dla materiału. W oryginalnych eksperymentach Darcy ’ ego używał piasków o różnych rozmiarach ziaren, jednak przewodność hydrauliczną można określić również dla skał litych, ponieważ większość skał ma pewną przestrzeń porów.
Po oryginalnych eksperymentach Darcy ’ ego przeprowadzono dalsze prace nad zrozumieniem fizycznych właściwości płynu i skały, które determinują skuteczne przewodnictwo hydrauliczne. Z tych eksperymentów stwierdzono, że
\
gdzie \(k\) jest wewnętrzną przepuszczalnością porowatego ośrodka (ciała stałego), \(\eta\) jest lepkością dynamiczną płynu, a \(\gamma = \Rho g\) jest ciężarem właściwym płynu, który zależy od gęstości płynu, \(\Rho\) i grawitacji, \(g\).
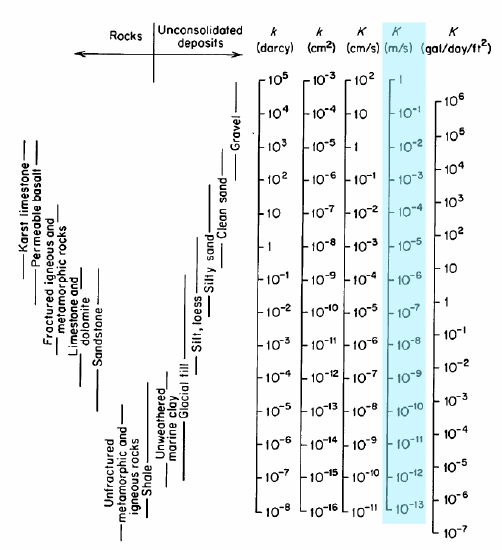
wyróżniona kolumna na rysunku to K, przewodność hydrauliczna w \(\frac{m} {s}\); są to jednostki, których będziemy używać. Przewodność hydrauliczna jest również czasami podawana pod względem wewnętrznej przepuszczalności, \(k\), z jednostkami darcys lub cm2. Pełny zakres wartości przewodności hydraulicznej wynosi 1-10-13 \(\frac{m}{s}\). Eksperymenty takie jak Darcy ’ ego są używane do pomiaru K w materiałach rzeczywistych.
szybkość rozładowania \(Q\) jest strumieniem objętościowym (\(m^3/S\)), ale zwykle myślimy o przepływie płynu w kategoriach prędkości lub prędkości. Pytania dotyczące wyładowania można przestawić dzieląc przez pole, aby zdefiniować strumień Darcy ’ ego
\ \]
lub w kategoriach wewnętrznej przepuszczalności i gradientu ciśnienia,
\
gdzie \(\eta\) jest lepkością płynu (patrz poniżej wyprowadzenie drugiego równania).
należy zauważyć, że strumień Darcy ’ ego nie jest równy prędkości płynu, mimo że jest w jednostkach prędkości. Prędkość płynu znajduje się poprzez średnią prędkość liniową (\(v_a\)), która jest średnią prędkością wszystkich możliwych dróg płynu przez porowate media: ale znalezienie tej wartości jest poza zakresem tej klasy. Zamiast tego zauważymy, że prędkość płynu wynosi
\
gdzie \(\varphi\) to porowatość, A v to prędkość płynu. Porowatość, \(\varphi\) jest obliczana jako stosunek objętości pustej przestrzeni do całkowitej objętości materiału \(\varphi=\frac{V_{void}}{v_{tot}}\) i jest zwykle wyrażana jako ułamek między 0 a 1 lub jako procent. Zauważ, że jeśli \(\varphi \ leq\)1, to prędkość płynu jest większa niż strumień darcy ’ ego.
innym terminem, który pojawia się przy omawianiu przepływu przez skały i nieskonsolidowane Materiały, jest przepuszczalność. Podczas gdy porowatość jest faktycznym ułamkiem porów (pustek) w skale, pustki te mogą mieć różne kształty i różne połączenia, co wpływa na to, jak łatwo płyn może poruszać się w przestrzeni porów. Przepuszczalność jest miarą łatwości, z jaką ciecze i gazy mogą przechodzić przez skałę. Im bardziej skonsolidowany Materiał, tym niższa jego przepuszczalność. Tak więc „luźne” materiały, takie jak żwir, mają wysoką przepuszczalność. Niektóre skały mogą również mieć anizotropową przepuszczalność, co oznacza, że płyny mogą płynąć łatwo w jednym kierunku, ale nie w innym. Przykładem skały o anizotropowej przepuszczalności jest łupek. Płyny mogą łatwo poruszać się w warstwie łupków, ale nie mogą poruszać się po warstwach.
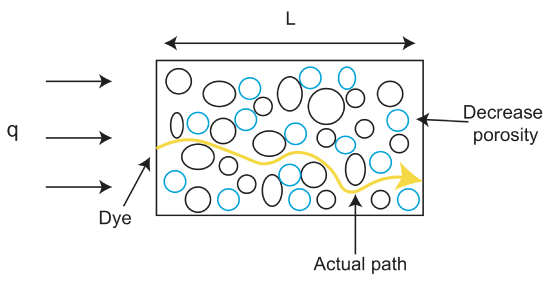
prędkość płynu
zróbmy podstawowy przykład.
otrzymujemy, że \(q=2 \ frac{m} {min}\) i \(\varphi\) wynosi 25% i chcemy znaleźć prędkość płynu.
najpierw zamieniamy 25% Na 0.25.
wtedy, \(v = \ frac{2}{0.25}\frac{m}{min}\)
i
\(v=8 \frac{m}{min}\) jest prędkością płynu.
głowica hydrauliczna
Wracając do eksperymentów Darcy ’ ego, czym jest proces fizyczny napędzający przepływ płynu przez flume?
termin \(\frac{dh}{DX} \) jest określany jako głowica hydrauliczna, która jest ciśnieniem cieczy wynikającym z masy płynu w stosunku do pewnego miejsca odniesienia: gradientu ciśnienia. Jednak \(\frac{dh}{dx}\) nie ma jednostek ciśnienia na jednostkę długości, więc dlaczego nazywa się to głowicą hydrauliczną?
zastanówmy się, jakie jest Ciśnienie w strumieniu w eksperymentach Darcy ’ ego. W celu przeprowadzenia eksperymentów, Darcy ’ s miał zbiornik wody na górnym końcu flume, zapewniający stały poziom wody na szczycie flume, równoważny wysokości flume, \(h_1\). Podobnie na dnie znajdował się zbiornik o stałym poziomie wody równym \(h_2\). Dlatego ciśnienie płynu w każdym ze zbiorników ze względu na ciężar wody jest podane przez \(P = \Rho g h\). Gradient ciśnienia od góry do dołu pióropusza jest wtedy
\
lub
\
podstawiając do prawa Darcy ’ ego,
\ & =\frac{K}{\rho g}\frac{dp}{dx} \end{align}. \]
Przypomnijmy, z góry, że przewodność hydrauliczna może być zapisana w kategoriach przenikalności wewnętrznej jako \(k = k\frac{\gamma}{\eta}\), co jest równoważne \(k\frac{\Rho g}{\eta}\) lub przestawianie, \(\frac{K}{\Rho g} = \frac{k}{\eta}\). Dlatego możemy podstawić dwa równoważne wyrażenia dla prawa Darcy 'ego, z jednym intermsem gradientu wysokości,
\
i drugim pod względem gradientu ciśnienia,
\
Tak więc, \(\frac{dh}{dx}\) nazywa się głowicą hydrauliczną, ponieważ fizycznym pochodzeniem terminu w prawie Darcy’ ego jest gradient ciśnienia w płynie, który napędza przepływ.
woda opuszcza warstwę wodonośną
zróbmy teraz przykład obliczania prędkości płynu wody wchodzącej do warstwy wodonośnej. Na rysunku poniżej wysokość warstwy wodonośnej przedstawia topografię wzgórza przylegającego do doliny z potokiem. Woda wypływa z wysokiego ciśnienia (wysokości głowy) w kierunku doliny i opuszcza warstwę wodonośną przy strumieniu. Możemy użyć prawa Darcy ’ ego do oszacowania szybkości przepływu wody z warstwy wodonośnej.
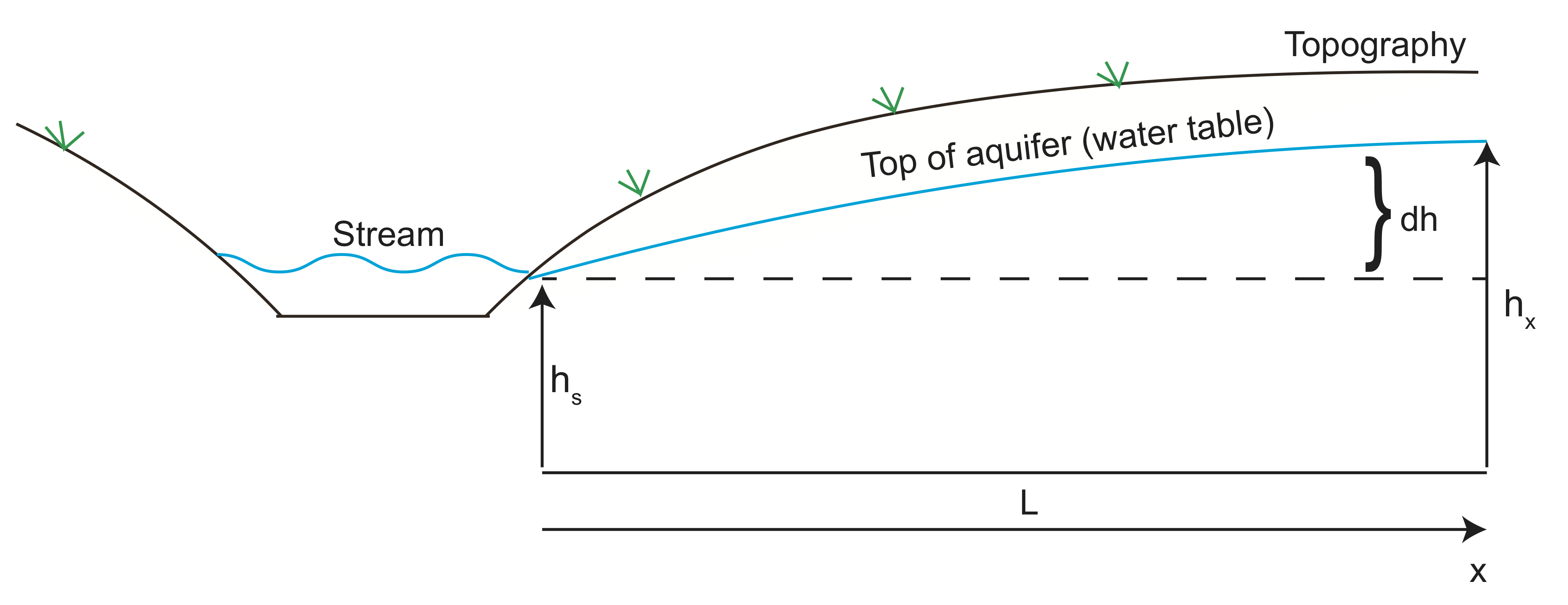
korzystając z obrazowania geofizycznego, wysokość warstwy wodonośnej znajduje się 10 m (\(dh\)) powyżej wysokości strumienia około 100 metrów (\(L\)) od siebie. Załóżmy, że przewodność hydrauliczna wynosi \ (K=10^{-6}\) m / s, a porowatość wynosi \(\varphi=30\)%.
strumień darcy jest
\
\
\
prędkość płynu jest
\
\
\
\
\

Laminar versus Turbulent Flow
jednym z domniemanych założeń prawa Darcy ’ ego jest to, że przepływ jest laminarny. Przepływ laminarny jest scharakteryzowany jako składający się z cienkich warstw lub laminae płynu wszystkie poruszające się równolegle do siebie. Natomiast przepływ turbulentny charakteryzuje się wirami, wirami i wirami, w których sąsiednie warstwy płynu rozchodzą się i podążają różnymi ścieżkami w dół strumienia.
jednym ze sposobów, w jaki możemy określić, czy płyn jest laminarny, czy burzliwy, jest obliczenie liczby Reynolda dla przepływu, zdefiniowanej jako
\
liczba Reynolda znajduje się poprzez rozważenie dwóch terminów w równowadze pędu dla przepływu. Pierwszym terminem jest siła bezwładności na jednostkę objętości, która napędza przepływ, \(\rho u\frac{du}{dx}\). Drugim terminem jest siła lepka na jednostkę objętości, która opiera się przepływowi, \(\eta \ frac{d^2U}{DX^2}\). Te dwa terminy muszą się równoważyć, więc możemy ustawić je równe,
\
następnie przepisujemy terminy, w uproszczony sposób, aby uchwycić tylko odpowiednie wymiary zmiennych. Aby to zrobić, przechodzimy przez to, co nazywa się analizą wymiarową, w której zastępujemy każdą zmienną, wartościami referencyjnymi, razy niewymiarową postać zmiennej.
na przykład dla wyrażenia \(x\) jest przepisywane jako po prostu \(L x’\), gdzie \(L\) jest długością odniesienia (głębokością płynu) i \(x’\) jest odległością wymiarową. Podobnie, let \(u = u_o u’\). Podstawiając je do równania, otrzymujemy
\
następnie łączymy wartości stałe z przodu
\
zauważ, że kombinacja zmiennych z przodu jest liczbą Reynolda
\
gdzie zmiennymi są \(u_o\) prędkość przepływu, l głębokość płynu i zmienne, które widzieliśmy wcześniej, \(\rho\) gęstość płynu i \(\eta\) lepkość płynu. Przechodząc przez tę analizę, odkrywamy, że każdy przepływ, który charakteryzuje się równowagą tych dwóch wyrażeń, może być porównany przez prostą znajomość wartości liczby Reynoldsa. Na przykład, jeśli jeden przepływ ma lepkość, która jest 10 razy lepkość w innym przepływie, dwa przepływy zachowają się tak samo, gdy gęstość (lub prędkość lub długość) jest również zwiększona o współczynnik 10 dla przypadku wyższej lepkości; to znaczy, Liczba Reynoldsa dla dwóch przepływów jest taka sama.
aby mieć przepływ, Liczba Reynolda musi być mniejsza niż około 1-10 (laminarna). Dla \ (Re>1-10\) przepływ nie jest ściśle laminarny, ale nie jest jeszcze burzliwy (nieliniowy, nie-laminarny). Aby mieć przepływ turbulentny, Liczba Reynolda musi być większa niż około 2000.
zrozumienie, że stałe w liczniku i mianowniku wpływają na charakterystykę przepływu w przeciwny sposób, pomaga również zastanowić się, jak różne płyny będą zachowywać się w podobnych warunkach zewnętrznych. Na przykład gęstszy płyn, który ma również dużą prędkość, będzie miał wyższe Re i wykazuje burzliwe zachowanie. W przeciwieństwie do tego, płyn, taki jak lód, który ma wysoką lepkość i porusza się bardzo wolno, będzie miał niski Re i prawdopodobnie będzie miał przepływ laminarny. Wysoka lepkość lodu działa stabilizująco na przepływ. Jako inny przykład, rozważmy dwa płyny, które poruszają się z tą samą prędkością, zachowują się inaczej, jeśli inne wartości liczby Reynolda \(\frac{\Rho L}{\mu}\) są różne. Dlatego rodzaj przepływu zależy nie tylko od prędkości przepływu, ale od kombinacji zmiennych w liczbie Reynolda.
zastosowanie przepływu Darcy 'ego
prawo Darcy’ ego jest głównym równaniem, które reguluje przepływ w warstwach wodonośnych i studniach. Bez niego nie bylibyśmy w stanie wiercić studni ani zrozumieć ruchu wody w warstwach wodonośnych, zwłaszcza w środkowej dolinie Kalifornii, gdzie oba te pomysły są kluczowe zarówno dla wydajności rolnictwa, jak i osiadania wód gruntowych.
