regressie naar het gemiddelde is een algemeen statistisch fenomeen dat ons kan misleiden wanneer we de wereld observeren. Leren herkennen wanneer regressie naar het gemiddelde in het spel is, kan ons helpen om verkeerde interpretaties van gegevens te voorkomen en patronen te zien die niet bestaan.

***

Het is belangrijk om gevallen van slecht oordeel te minimaliseren en de zwakke plekken in onze redenering aan te pakken. Leren over regressie naar het gemiddelde kan ons helpen.Nobelprijswinnaar Daniel Kahneman schreef een boek over vooroordelen die onze redenering vertroebelen en onze perceptie van de werkelijkheid vervormen. Het blijkt dat er een hele reeks logische fouten is die we begaan omdat onze intuïtie en hersenen niet goed omgaan met eenvoudige statistieken. Een van de fouten die hij onderzoekt in snel en langzaam denken is de beruchte regressie naar het gemiddelde.het begrip regressie tot het gemiddelde werd voor het eerst uitgewerkt door Sir Francis Galton. De regel luidt dat, in elke reeks met complexe fenomenen die afhankelijk zijn van vele variabelen, waar kans is betrokken, extreme uitkomsten de neiging om te worden gevolgd door meer gematigde degenen.

In het zoeken naar wijsheid geeft Peter Bevelin het voorbeeld van John, die ontevreden was over de prestaties van nieuwe werknemers, dus hij zette hen in een vaardigheidsversterkend programma waar hij de vaardigheden van de werknemers meet:

hun scores zijn nu hoger dan ze op de eerste test waren. John ’s conclusie:” het vaardigheidsverhogende programma veroorzaakte de verbetering van vaardigheden.”Dit is niet noodzakelijk waar. Hun hogere scores kunnen het resultaat zijn van regressie naar het gemiddelde. Aangezien deze individuen werden gemeten als zijnde op de lage kant van de schaal van vaardigheid, zouden ze een verbetering hebben getoond, zelfs als ze niet het vaardigheidsverhogende programma hadden genomen. En er kunnen vele redenen zijn voor hun eerdere prestaties — stress, vermoeidheid, ziekte, afleiding, enz. Hun ware vermogen is misschien niet veranderd.

onze prestaties variëren altijd rond een gemiddelde werkelijke prestaties. Extreme prestaties hebben de neiging om de volgende keer minder extreem te worden. Waarom? Het testen van metingen kan nooit exact zijn. Alle metingen bestaan uit één waar deel en één willekeurig foutdeel. Wanneer de metingen extreem zijn, zijn ze waarschijnlijk deels veroorzaakt door toeval. Kans zal waarschijnlijk minder bijdragen aan de tweede keer dat we prestaties meten.

als we overschakelen van de ene manier om iets te doen naar de andere alleen maar omdat we niet succesvol zijn, is het zeer waarschijnlijk dat we het de volgende keer beter doen, zelfs als de nieuwe manier om iets te doen gelijk of slechter is.

Dit is een van de redenen waarom het gevaarlijk is om uit kleine steekproefgrootten te extrapoleren, omdat de gegevens mogelijk niet representatief zijn voor de distributie. Het is ook de reden waarom James March stelt dat hoe langer iemand blijft in hun baan, ” hoe minder het waarschijnlijke verschil tussen de waargenomen record van prestaties en de werkelijke capaciteit.”Er kan van alles gebeuren op de korte termijn, vooral bij elke inspanning die een combinatie van vaardigheid en geluk met zich meebrengt. (De verhouding van vaardigheid tot geluk beïnvloedt ook de regressie naar het gemiddelde.)

regressie tot het gemiddelde

De effecten van regressie tot het gemiddelde kunnen vaak worden waargenomen in sport, waar het effect veel ongerechtvaardigde speculaties veroorzaakt.in snel en langzaam denken herinnert Kahneman zich dat hij naar de skischans van mannen keek, een discipline waar de eindscore een combinatie is van twee afzonderlijke sprongen. Zich bewust van de regressie naar het gemiddelde, Kahneman was geschrokken om de voorspellingen van de commentator over de tweede sprong te horen. Hij schrijft:

Noorwegen had een geweldige eerste sprong; hij zal gespannen zijn, in de hoop zijn voorsprong te beschermen en het waarschijnlijk slechter doen” of “Zweden had een slechte eerste sprong en nu weet hij dat hij niets te verliezen heeft en zal ontspannen zijn, wat hem zou moeten helpen het beter te doen.

Kahneman wijst erop dat de commentator de regressie tot het gemiddelde had opgemerkt en met een verhaal kwam waarvoor geen causaal bewijs was (zie narratieve misvatting). Dit wil niet zeggen dat zijn verhaal niet waar kan zijn. Misschien, als we de hartslag meten voor elke sprong, zouden we zien dat ze meer ontspannen zijn als de eerste sprong slecht was. Maar daar gaat het niet om. Het punt is, regressie naar het gemiddelde gebeurt wanneer geluk een rol speelt, zoals het deed in de uitkomst van de eerste sprong.

de les uit sport is van toepassing op elke activiteit waarbij kans een rol speelt. We hechten vaak verklaringen van onze invloed op een bepaald proces aan de vooruitgang of het gebrek daaraan.

in werkelijkheid is de wetenschap van de prestaties complex, afhankelijk van de situatie en vaak is veel van wat we denken dat binnen onze controle is echt willekeurig.

bij skischansen zal een sterke wind tegen de springer ertoe leiden dat zelfs de beste atleet middelmatige resultaten laat zien. Ook een sterke wind en ski-omstandigheden in het voordeel van een middelmatige jumper kan leiden tot een aanzienlijke, maar een tijdelijke hobbel in zijn resultaten. Deze effecten zullen echter verdwijnen zodra de omstandigheden veranderen en de resultaten zullen weer normaal worden.

Dit kan ernstige gevolgen hebben voor coaching en prestatietracking. De regressieregels suggereren dat we bij het evalueren van prestaties of aanwervingen meer moeten vertrouwen op trackrecords dan op resultaten van specifieke situaties. Anders zijn we geneigd teleurgesteld te worden.toen Kahneman een lezing gaf aan de Israëlische luchtmacht over de psychologie van effectieve training, deelde een van de officieren zijn ervaring dat het loven van lof aan zijn ondergeschikten leidde tot slechtere prestaties, terwijl schelden leidde tot een verbetering in latere inspanningen. Als gevolg daarvan was hij grootmoedig geworden met negatieve feedback en was hij nogal op zijn hoede voor het geven van te veel lof.

Kahneman merkte onmiddellijk dat het een regressie was naar het gemiddelde op het werk. Hij illustreerde de misvatting door een eenvoudige oefening die u misschien zelf wilt proberen. Hij tekende een cirkel op een schoolbord en vroeg de officieren een voor een om een stuk krijt te gooien in het midden van de cirkel met hun rug naar het schoolbord. Hij herhaalde het experiment en nam de prestaties van elke officier op in de eerste en tweede proef.

natuurlijk deden degenen die het bij de eerste poging ongelooflijk goed deden het bij de tweede poging slechter en vice versa. De misvatting werd meteen duidelijk: de verandering in de prestaties gebeurt natuurlijk. Dat wil weer niet zeggen dat feedback er helemaal niet toe doet – misschien wel, maar de officier had geen bewijs om te concluderen dat het wel zo was.

de onvolmaakte correlatie en kans

Op dit punt vraagt u zich misschien af waarom de regressie naar het gemiddelde plaatsvindt en hoe we ervoor kunnen zorgen dat we ons ervan bewust zijn wanneer het zich voordoet.

om regressie tot het gemiddelde te begrijpen, moeten we eerst correlatie begrijpen.

de correlatiecoëfficiënt tussen twee maten, die varieert tussen -1 en 1, is een maat voor het relatieve gewicht van de factoren die zij delen. Bijvoorbeeld, twee verschijnselen met weinig factoren gedeeld, zoals gebotteld waterverbruik versus zelfmoordpercentage, moet een correlatiecoëfficiënt van dicht bij 0 hebben. Dat wil zeggen, als we naar alle landen in de wereld zouden kijken en de zelfmoordcijfers van een bepaald jaar zouden berekenen ten opzichte van het verbruik per hoofd van de bevolking van gebotteld water, dan zou de plot helemaal geen patroon vertonen.

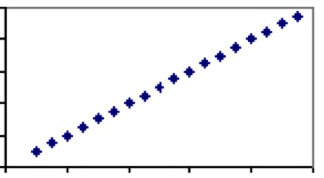
integendeel, er zijn maatregelen die uitsluitend afhankelijk zijn van dezelfde factor. Een goed voorbeeld hiervan is de temperatuur. De enige factor die de temperatuur bepaalt – de snelheid van moleculen — wordt gedeeld door alle schalen, vandaar dat elke graad in Celsius precies één overeenkomstige waarde in Fahrenheit zal hebben. Daarom zal de temperatuur in Celsius en Fahrenheit een correlatiecoëfficiënt van 1 hebben en zal de plot een rechte lijn zijn.

Er zijn weinig of geen verschijnselen in de Humane Wetenschappen met een correlatiecoëfficiënt van 1. Er zijn er echter genoeg waar de associatie zwak tot matig is en er is enige verklarende kracht tussen de twee verschijnselen. Denk aan de correlatie tussen lengte en gewicht, die ergens tussen 0 en 1 zou landen. Terwijl vrijwel elke driejarige lichter en korter zal zijn dan elke volwassen man, zullen niet alle volwassen mannen of driejarigen van dezelfde lengte hetzelfde wegen.

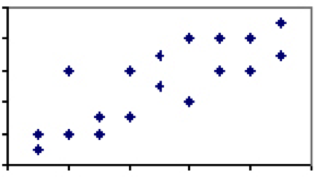
Deze variatie en de overeenkomstige lagere correlatie impliceert dat, hoewel hoogte over het algemeen een goede voorspeller is, er duidelijk andere factoren dan de hoogte in het spel zijn. Wanneer de correlatie tussen twee maatregelen minder dan perfect is, moeten we oppassen voor de effecten van regressie tot het gemiddelde.

Kahneman nam een algemene regel in acht: wanneer de correlatie tussen twee scores onvolmaakt is, zal er regressie zijn naar het gemiddelde.

Dit lijkt in eerste instantie verwarrend en niet erg intuïtief, maar de mate van regressie tot het gemiddelde is direct gerelateerd aan de mate van correlatie van de variabelen. Dit effect kan worden geïllustreerd met een eenvoudig voorbeeld.

neem aan dat u op een feestje bent en vraag waarom zeer intelligente vrouwen de neiging hebben om mannen te trouwen die minder intelligent zijn dan ze zijn. De meeste mensen, zelfs die met enige opleiding in de statistiek, zullen snel springen in met een verscheidenheid van causale verklaringen variërend van het vermijden van concurrentie tot de angsten van eenzaamheid die deze vrouwen geconfronteerd. Een onderwerp van zo ‘ n controverse zal waarschijnlijk een groot debat op gang brengen.

nu, wat als we ons afvragen waarom de correlatie tussen de intelligentiescores van echtgenoten minder dan perfect is? Deze vraag is nauwelijks zo interessant en er is weinig te raden – we weten allemaal dat dit waar is. De paradox ligt in het feit dat de twee vragen toevallig algebraïsch equivalent zijn. Kahneman legt uit:

als de correlatie tussen de intelligentie van echtgenoten minder dan perfect is (en als mannen en vrouwen gemiddeld niet verschillen in intelligentie), dan is het een wiskundige onvermijdelijkheid dat zeer intelligente vrouwen zullen trouwen met echtgenoten die gemiddeld minder intelligent zijn dan zij zijn (en vice versa, natuurlijk). De waargenomen regressie tot het gemiddelde kan niet interessanter of verklaarbaarder zijn dan de onvolmaakte correlatie.

aangenomen dat de correlatie onvolmaakt is, is de kans dat twee partners de top 1% vertegenwoordigen in termen van een kenmerk veel kleiner dan één partner die de top 1% vertegenwoordigt en de andere – de bottom 99%.

de oorzaak, het Effect en de behandeling

We moeten vooral voorzichtig zijn met de regressie naar het gemiddelde fenomeen wanneer we proberen causaliteit tussen twee factoren vast te stellen. Wanneer correlatie onvolmaakt is, zal het beste altijd slechter lijken te worden en het slechtste zal na verloop van tijd beter lijken te worden, ongeacht eventuele aanvullende behandeling. Dit is iets dat de algemene media en soms zelfs getrainde wetenschappers niet herkennen.

neem het voorbeeld dat Kahneman geeft:

depressieve kinderen die met een energiedrank worden behandeld, verbeteren aanzienlijk over een periode van drie maanden. Ik verzon deze krantenkop, maar het feit dat het rapporteert is waar: als u een groep depressieve kinderen enige tijd met een energiedrank zou behandelen, zouden ze een klinisch significante verbetering vertonen. Het is ook zo dat depressieve kinderen die enige tijd op hun hoofd staan of een kat twintig minuten per dag knuffelen ook verbetering zullen vertonen.

wanneer dergelijke krantenkoppen zich voordoen, is het zeer verleidelijk om tot de conclusie te komen dat energiedranken, op het hoofd staan of katten omhelzen, allemaal perfect levensvatbare behandelingen zijn voor depressie. Deze gevallen belichamen echter opnieuw de achteruitgang naar het gemiddelde.:

depressieve kinderen zijn een extreme groep, ze zijn depressiever dan de meeste andere kinderen—en extreme groepen dalen in de loop van de tijd tot het gemiddelde. De correlatie tussen depressiescores bij opeenvolgende testen is minder dan perfect, dus er zal regressie zijn naar het gemiddelde: depressieve kinderen zullen in de loop van de tijd iets beter worden, zelfs als ze geen katten omhelzen en geen Red Bull drinken.

We schrijven vaak ten onrechte een specifiek beleid of een specifieke behandeling toe als de oorzaak van een effect, wanneer de verandering in de extreme groepen toch zou hebben plaatsgevonden. Dit levert een fundamenteel probleem op: hoe kunnen we weten of de effecten echt zijn of gewoon te wijten zijn aan variabiliteit?

gelukkig is er een manier om te vertellen tussen een echte verbetering en regressie naar het gemiddelde. Dat is de invoering van de zogenaamde controlegroep, die naar verwachting alleen door regressie zal verbeteren. Het doel van het onderzoek is om te bepalen of de behandelde groep meer verbetert dan regressie kan verklaren.

in reële situaties met de prestaties van specifieke individuen of teams, waarbij de enige echte benchmark de prestaties uit het verleden is en er geen controlegroep kan worden ingevoerd, kunnen de effecten van regressie moeilijk, zo niet onmogelijk te ontwarren zijn. We kunnen vergelijken met industriegemiddelde, leeftijdsgenoten in de cohortgroep of historische verbeterpercentages, maar geen van deze zijn perfecte maatstaven.

***

gelukkig is het bewustzijn van de regressie naar het gemiddelde fenomeen zelf al een grote eerste stap naar een zorgvuldiger benadering van geluk en prestaties.

als er iets te leren valt van de regressie naar het gemiddelde is het het belang van track records in plaats van te vertrouwen op eenmalige succesverhalen. Ik hoop dat de volgende keer dat je tegenkomt een extreme kwaliteit gedeeltelijk beheerst door het toeval zul je beseffen dat de effecten zijn waarschijnlijk terug te nemen in de tijd en zal uw verwachtingen dienovereenkomstig aan te passen.

wat te lezen

• Upgrade uw denken met 113 mentale modellen uitgelegd.
• lees over denken op het tweede niveau, zodat u negatieve gevolgen kunt vermijden.