Noot van de redactie

het volgende onderzoeksrapport werd opgesteld voor Professor Judit Kardos’ Math 255 class, gehouden aan het College van New Jersey. Dit was een 3-credit inleidende cursus in de geschiedenis van de wiskunde. Dit rapport werd meegeteld voor 30% van de eindklassering. Het is een voorbeeld van het soort historische onderzoeksstudenten kunnen doen met behulp van secundaire bronnen.Leonard Eulers oplossing voor het probleem van de brug van Königsberg

Königsberg

ons verhaal begint in de 18e eeuw, in het schilderachtige stadje Königsberg, Pruisen aan de oevers van de Pregel. In 1254 stichtten de Duitse ridders de stad Königsberg onder leiding van de Boheemse koning Ottoker II na hun tweede kruistocht tegen de Pruisen. In de Middeleeuwen werd Königsberg een zeer belangrijke stad en handelscentrum met zijn strategische ligging aan de rivier. Kunstwerken uit de achttiende eeuw tonen Königsberg als een bloeiende stad, waar vloten van schepen vullen de Pregel, en hun handel biedt een comfortabele levensstijl voor zowel de lokale kooplieden en hun families. Door de gezonde economie konden de inwoners van de stad zeven bruggen over de rivier bouwen, waarvan de meeste verbonden waren met het eiland Kneiphof; hun locaties zijn te zien op de begeleidende foto .

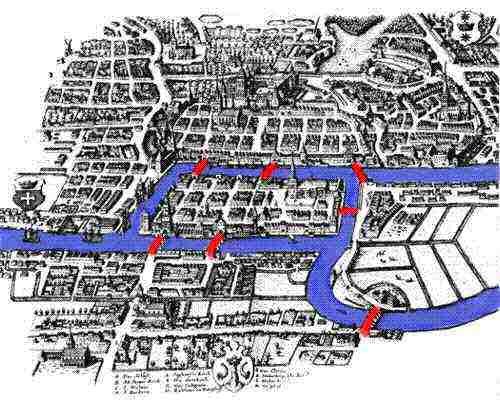
omdat de rivier rond Kneiphof stroomde, wat letterlijk pubwerf betekent, en een ander eiland, verdeelde het de stad in vier verschillende regio ‘ s. De zeven bruggen werden Blacksmith ’s bridge, Connecting Bridge, Green Bridge, Merchant’ s Bridge, Wooden Bridge, High Bridge en Honey Bridge genoemd. Volgens de overlevering brachten de inwoners van Königsberg zondagmiddag door in hun prachtige stad. Tijdens het lopen besloten de mensen van de stad om een spel voor zichzelf te maken, hun doel was om een manier te bedenken waarop ze door de stad konden lopen, waarbij ze elk van de zeven bruggen slechts één keer overstaken. Hoewel geen van de inwoners van Königsberg een route kon bedenken die hen in staat zou stellen om elk van de bruggen slechts één keer over te steken, konden ze nog steeds niet bewijzen dat het onmogelijk was. Gelukkig voor hen was Königsberg niet ver van St. Petersburg, de thuisbasis van de beroemde wiskundige Leonard Euler.

Euler en het Brugprobleem

waarom zou Euler zich bezighouden met een probleem dat zo los staat van het gebied van de wiskunde? Waarom zou zo ‘ n groot wiskundige veel tijd besteden aan een triviaal probleem zoals het Brugprobleem in Königsberg? Euler was duidelijk een drukbezet man, die tijdens zijn leven meer dan 500 boeken en papers publiceerde. Alleen al in 1775 schreef hij gemiddeld één wiskundig artikel per week, en tijdens zijn leven schreef hij over verschillende onderwerpen naast wiskunde, waaronder mechanica, optica, astronomie, navigatie en hydrodynamica. Het is niet verwonderlijk dat Euler vond dat dit probleem triviaal was, verklaarde in een brief uit 1736 aan Carl Leonhard Gottlieb Ehler, burgemeester van Danzig, die hem vroeg om een oplossing voor het probleem :

. . . Zo ziet gij, edelmoedige Heer, hoe dit soort oplossingen weinig verband houdt met de wiskunde, en ik begrijp niet, waarom gij verwacht, dat een wiskundige het voortbrengt, meer dan iemand anders, want de oplossing is alleen gebaseerd op de rede, en de ontdekking ervan is niet afhankelijk van enig wiskundig Principe. Daarom Weet ik niet waarom zelfs vragen die zo weinig verband houden met de wiskunde sneller door wiskundigen worden opgelost dan door anderen.

hoewel Euler het probleem triviaal vond, was hij er nog steeds door geïntrigeerd. In een brief geschreven in hetzelfde jaar aan Giovanni Marinoni, een Italiaanse wiskundige en ingenieur, zei Euler ,

deze vraag is zo banaal, maar leek mij de aandacht waard in dat meetkunde, noch algebra, noch zelfs de kunst van het tellen voldoende was om het op te lossen.

Euler geloofde dat dit probleem gerelateerd was aan een onderwerp dat Gottfried Wilhelm Leibniz ooit had besproken en waar hij naar verlangde om mee te werken, iets waar Leibniz naar verwees als geometria situs, of meetkunde van positie. Deze zogenaamde meetkunde van positie is wat nu grafentheorie wordt genoemd, die Euler introduceert en gebruikt bij het oplossen van dit beroemde probleem.

Euler ‘ s Proof

Op 26 augustus 1735 presenteert Euler een document met de oplossing voor het brugprobleem in Konigsberg. Hij behandelt zowel dit specifieke probleem als een algemene oplossing met een willekeurig aantal landmassa ‘ s en een willekeurig aantal bruggen. Dit artikel, getiteld ‘Solutio problematis ad geometriam situs pertinentis’, werd later gepubliceerd in 1741 . Het artikel van Euler is verdeeld in eenentwintig genummerde alinea ‘s, en in wat volgt zal een vereenvoudigde versie van de alinea’ s van Euler worden gepresenteerd.

in de eerste twee alinea ‘ s van het bewijs van Euler introduceert hij het probleem van de brug van Konigsberg. In Paragraaf 1 stelt Euler dat hij van mening is dat dit probleem betrekking heeft op de meetkunde, maar niet op de meetkunde die zijn tijdgenoten goed kennen en die metingen en berekeningen omvat, maar op een nieuw soort Meetkunde, die Leibniz de meetkunde van positie noemt. Vervolgens legt Euler in Paragraaf 2 aan zijn publiek uit hoe het Konigsberg-probleem werkt. Euler gaf een schets van het probleem (zie Figuur 1 van Euler), en noemde de zeven verschillende bruggen: a, b, c, d, e, f en g. In deze paragraaf stelt hij de algemene vraag van het probleem, “kan men erachter komen of het mogelijk is om elke brug precies één keer over te steken?”

Euler ’s Figuur 1 uit’ Solutio problematis ad geometriam situs pertinentis, ‘ eneström 53

Na het stellen van de algemene vraag die hij probeert op te lossen, begint Euler verschillende methoden te verkennen om een oplossing te vinden. In Paragraaf 3 vertelt Euler de lezer dat om dit specifieke probleem op te lossen, hij alle mogelijke paden zou kunnen opschrijven, maar deze techniek zou veel tijd in beslag nemen en niet werken voor grotere configuraties met meer bruggen en landmassa ‘ s. Vanwege deze problemen besloot Euler een andere methode te kiezen om dit probleem op te lossen.

in Paragraaf 4 begint hij het probleem te vereenvoudigen door een handig systeem uit te vinden om het oversteken van een brug weer te geven. Euler besluit dat in plaats van de kleine letters te gebruiken om het oversteken van een brug weer te geven, hij de hoofdletters zou schrijven die de landmassa ‘ s vertegenwoordigen. Bijvoorbeeld, refererend aan zijn figuur 1, zou AB een reis betekenen die begon in landmassa A, en eindigde in B. Bovendien, als na het reizen van landmassa A naar B, iemand besluit om te verhuizen naar landmassa D, zou dit simpelweg worden aangeduid, ABD. In Paragraaf 5 zet Euler zijn discussie over dit proces voort en legt hij uit dat in ABDC, hoewel er vier hoofdletters zijn, slechts drie bruggen zijn overgestoken. Euler legt uit dat het niet uitmaakt hoeveel bruggen er zijn, er nog een letter zal zijn om de noodzakelijke kruising weer te geven. Om deze reden waren voor het gehele probleem van de brug van Königsberg zeven bruggen nodig, en dus acht hoofdletters.

in Paragraaf 6 gaat Euler verder met het toelichten van de details van zijn methode. Hij vertelt de lezer dat als er meer dan één brug is die kan worden overgestoken wanneer je van de ene landmassa naar de andere gaat, het niet uitmaakt welke brug wordt gebruikt. Hoewel er bijvoorbeeld twee bruggen zijn, a en b, die een reiziger van A naar B kunnen brengen, maakt het met Euler ‘ s notatie niet uit welke brug wordt genomen. In deze paragraaf bespreekt Euler ook het specifieke probleem waarmee hij te maken heeft. Aan de hand van zijn oorspronkelijke figuur legt hij uit dat het probleem van de Königsberg precies acht letters nodig heeft, waarbij de paren van (A, B) en (A, C) precies twee keer naast elkaar moeten verschijnen,ongeacht welke letter het eerst verschijnt. Bovendien moeten de paren (A, D), (B, D), en (C, D) exact één keer samen voorkomen om een pad dat elke brug één keer kruist te laten bestaan.

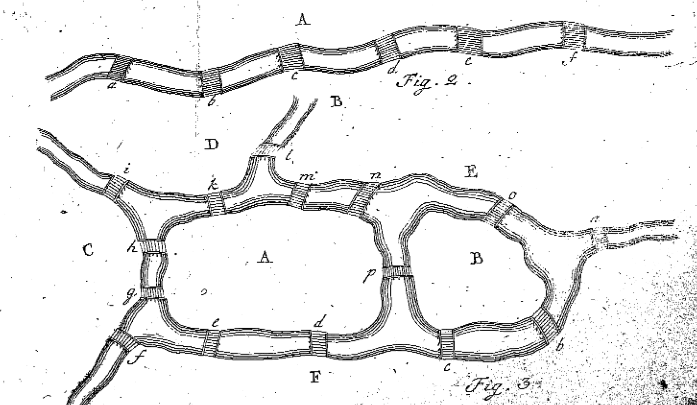
Euler ’s Figures 2 and 3 from’ Solutio problematis ad geometriam situs pertinentis, ‘ eneström 53

In paragraaf 7 informeert Euler de lezer dat hij ofwel een achtlettersequentie moet vinden die aan het probleem voldoet, ofwel dat hij moet bewijzen dat een dergelijke reeks niet bestaat. Voordat hij dit doet voor het probleem van de brug van Königsberg, besluit hij een regel te vinden om te ontdekken of er een pad bestaat voor een meer algemeen probleem. Dat doet hij in paragraaf 8 door te kijken naar veel eenvoudiger voorbeelden van landmassa ‘ s en bruggen. Euler tekent Figuur 2, en hij begint de situaties te beoordelen waar Regio A doorheen wordt gereisd. Euler stelt dat als brug a eenmaal wordt afgelegd, a ofwel de plaats was waar de reis begon Of eindigde, en daarom slechts één keer werd gebruikt. Als de bruggen a, b en c allemaal één keer worden afgelegd, wordt A precies twee keer gebruikt, ongeacht of het de begin-of eindplaats is. Op dezelfde manier, als vijf bruggen naar A leiden, zou de landmassa A precies drie keer in de reis voorkomen. Euler stelt dat, ” in het algemeen, als het aantal bruggen een oneven getal is, en als het met één wordt verhoogd, dan is het aantal voorvallen van A de helft van het resultaat.”Met andere woorden, als er een oneven aantal bruggen is die A verbinden met andere landmassa’ s, voeg dan één bij het aantal bruggen, en deel het door twee, om erachter te komen hoeveel keer A in totaal gebruikt moet worden in het pad, waar elke brug slechts één keer gebruikt wordt (d.w.z. Totaal aantal keren dat A een oneven # van bruggen heeft = (# Van Bruggen-1) / 2). met behulp van dit feit Lost Euler in Paragraaf 9 het probleem van de brug van Königsberg op. In dat geval, omdat er vijf bruggen zijn die naar A leiden, moet het drie keer voorkomen (zie zijn figuur 1 hierboven). Op dezelfde manier moeten B, C en D twee keer verschijnen omdat ze allemaal drie bruggen hebben die naar hen leiden. Dus 3(Voor A) + 2(Voor B) + 2(voor C) + 2 (Voor D) = 9, maar Euler zei al dat er slechts acht voorvallen moeten zijn voor de zeven bruggen. Dit is een contradictie! Daarom is het onmogelijk om de bruggen in de stad Königsberg één keer te bewandelen. Het einde, of is het? Hoewel de inwoners van Königsberg blij mogen zijn met deze oplossing, was de grote wiskundige Leonhard Euler niet tevreden. Euler vervolgt zijn bewijs om meer algemene situaties aan te pakken.

Euler ’s generalisatie

in paragraaf 10 vervolgt Euler zijn discussie met de opmerking dat als de situatie alle landmassa’ s met een oneven aantal bruggen betreft, het mogelijk is om uit te maken of een reis met elke brug slechts één keer kan worden gemaakt. Euler stelt dat als de som van het aantal keren dat elke letter moet verschijnen één meer is dan het totale aantal bruggen, een reis kan worden gemaakt. Echter, als het aantal voorvallen groter is dan één meer dan het aantal bruggen, kan een reis niet worden gemaakt, zoals het probleem van de brug van Königsberg. Dit komt omdat de regel, die Euler geeft voor een oneven aantal bruggen, met behulp van zijn figuur 2, geldt voor de algemene situatie of er slechts één andere landmassa of meer dan één is.

in de paragrafen 11 en 12 behandelt Euler de situatie waarin een regio een even aantal bruggen heeft. Deze situatie komt niet voor in het Königsberg-probleem en is daarom tot nu toe genegeerd. In de situatie met een landmassa X met een even aantal bruggen kunnen twee gevallen voorkomen. Het eerste geval is wanneer X het startpunt is voor de reis. In dit geval verschijnt X tweemaal, eenmaal als startpunt en opnieuw als eindpunt. In het andere geval is X niet het uitgangspunt. Als dit zou gebeuren, zou X slechts één keer verschijnen, omdat de reis via de ene brug zou moeten binnenkomen en onmiddellijk zou moeten vertrekken via de enige andere beschikbare brug. Ook als er vier bruggen verbonden zijn aan X hangt het aantal keren dat X voorkomt af van of het al dan niet een startpunt is. Als de reis in X begint, moet ze drie keer verschijnen, maar als ze niet in X begint, zou ze slechts twee keer verschijnen. Dus in het algemeen, als X heeft een even aantal bruggen bevestigd, dan als de reis niet begint in X, X verschijnt de helft van het aantal keren als bruggen (d.w.z. Gevallen van X waarbij X even is en niet het beginpunt = (#van Bruggen) / 2). Als de reis begint in X dan verschijnt X de helft van het aantal keren als bruggen, plus één (dat wil zeggen gevallen van X waar X gelijk is en startpunt = ((#van Bruggen) / 2) + 1).

in de paragrafen 13 tot en met 15 legt Euler uit hoe te achterhalen of een pad dat elke brug eenmaal en slechts eenmaal gebruikt, bestaat en geeft hij zijn eigen voorbeeld om te laten zien hoe het werkt. Euler legt eerst zijn eenvoudige zes-stappen methode uit om een algemene situatie op te lossen met landmassa ‘ s gedeeld door rivieren en verbonden door bruggen. Eerste Euler geeft elke landmassa aan met een hoofdletter. Ten tweede neemt hij het totale aantal bruggen, voegt er een toe en schrijft dit boven de grafiek die hij gaat maken. Vervolgens neemt hij de hoofdletters, zet ze in een kolom, en naast hen schrijft het aantal bruggen. Ten vierde geeft hij met sterretjes de landmassa ‘ s aan die een even aantal bruggen hebben. Vervolgens schrijft hij naast elk even getal ½ van het getal en naast elk oneven getal plaatst hij ½ van het getal plus één. Tot slot voegt Euler de getallen in de rechter kolom toe en als de som één kleiner is dan of gelijk is aan het aantal bruggen plus één, dan is de vereiste reis mogelijk. Het is echter belangrijk op te merken dat als de som één minder is dan het aantal bruggen plus één, dan moet de reis beginnen bij een van de landmassa ‘ s gemarkeerd met een sterretje. Als de som gelijk is aan het aantal bruggen plus één, moet de reis beginnen in een gebied dat niet met een sterretje is gemarkeerd.

voorbeelden

met behulp van het Konigsberg probleem als zijn eerste voorbeeld Euler toont het volgende:

aantal bruggen = 7, Aantal bruggen plus één = 8

Regio bruggen tijden regio moet verschijnen

A 5 3

B 3 2

C 3 2

d 3 2

echter, 3 + 2 + 2 + 2 = 9, dat is meer dan 8, dus de reis is onmogelijk.

omdat dit voorbeeld vrij basisch is, besluit Euler zijn eigen situatie te ontwerpen met twee eilanden, vier rivieren en vijftien bruggen. De situatie die Euler geschapen heeft is te zien in zijn figuur 3 hierboven. Euler probeert nu te achterhalen of er een pad is dat iemand toestaat om één keer over elke brug te gaan en slechts één keer. Euler volgt dezelfde stappen als hierboven, de naam van de vijf verschillende regio ‘ s met hoofdletters, en maakt een tabel om het te controleren als mogelijk is, zoals de volgende:

Aantal bruggen = 15, Aantal bruggen plus één = 16

Regio Bruggen Keer Gebied Moet worden Weergegeven

Een* 8 4

B* 4 2

C* 4 2

D 3 2

E 5 3

F* 6 3

verder, 4 + 2 + 2 + 2 + 3 + 3 = 16, die is gelijk aan het aantal van bruggen, plus één, wat betekent dat de reis is in feite mogelijk. Aangezien de som gelijk is aan het aantal bruggen plus één, moet de reis beginnen In D of E. Nu Euler weet dat het mogelijk is om een reis te maken, hoeft hij alleen maar te zeggen wat het pad zal zijn. Euler kiest voor het pad EaFbBcFdAeFfCgAhCiDkAmEnApBoElD, waar hij aangeeft welke bruggen worden gekruist tussen de letters die de landmassa ‘ s vertegenwoordigen. Hoewel deze informatie vreemd is, omdat de exacte brug er niet toe doet te weten dat een reis mogelijk is, is het nuttig bij het kiezen van een pad. Dit is een goed voorbeeld dat de methode laat zien die Euler zou gebruiken bij het oplossen van een probleem van deze aard.

Euler ’s Conclusions

in de volgende alinea’ s geeft Euler een andere manier om erachter te komen of een reis kan worden gemaakt met een verzameling landmassa ‘ s, bruggen en rivieren. In Paragraaf 16 wijst Euler erop dat het totaal van de aantallen die direct rechts van de landmassa ‘ s worden vermeld, tweemaal zo groot is als het totale aantal bruggen. Dit feit wordt later bekend als het handshaking lemma. In principe stelt het handshaking lemma dat elke brug twee keer wordt geteld, één keer voor elke landmassa waaraan hij is bevestigd. In paragraaf 17 stelt Euler verder dat de som van alle bruggen die naar elke regio Leiden gelijk is, aangezien de helft van dit aantal gelijk is aan het totale aantal bruggen. Dit is echter onmogelijk als er een oneven aantal landmassa ‘ s met een oneven aantal bruggen. Daarom bewijst Euler dat als er enkele oneven getallen aan landmassa ’s verbonden zijn, er een even aantal van deze landmassa’ s moet zijn.

echter, dit is niet genoeg om te bewijzen wanneer er een pad is waar elke brug één en slechts één keer wordt gebruikt, omdat het probleem van de brug in Königsberg een even aantal landmassa ‘ s heeft met een oneven aantal bruggen die er naartoe gaan. Daarom voegt Euler in de paragrafen 18 en 19 meer beperkingen toe. Euler legt uit dat aangezien het totaal van de aantallen bruggen die aan elke landmassa zijn bevestigd gelijk is aan tweemaal het aantal bruggen (zoals te zien is in het handshaking lemma), dus als je er twee bij optelt en dan door twee deelt, krijg je het aantal bruggen plus één. Dit getal is hetzelfde als het eerder gebruikte, dat wordt gebruikt om te vertellen of een pad mogelijk is. Als alle getallen even zijn, dan zal de derde kolom in de tabel optellen tot één minder dan het totale aantal bruggen plus één.

Euler legt vervolgens uit dat het duidelijk is dat als er twee landmassa ’s met een oneven aantal bruggen zijn, de reis altijd mogelijk zal zijn als de reis begint in een van de regio’ s met een oneven aantal bruggen. Dit is omdat als de even getallen worden gehalveerd, en elk van de oneven getallen worden verhoogd met één en gehalveerd, de som van deze helften zal gelijk zijn aan één meer dan het totale aantal bruggen. Echter, als er vier of meer landmassa ‘ s met een oneven aantal bruggen, dan is het onmogelijk voor er een pad. Dit komt omdat de som van de helften van de oneven getallen plus één samen met de som van alle helften van de even getallen de som van de derde kolom groter maakt dan het totale aantal bruggen plus één. Daarom bewees Euler net dat er hooguit twee landmassa ‘ s met een oneven aantal bruggen kunnen zijn. dit gezegd zijnde kan Euler nu zijn conclusies trekken over meer algemene vormen van het Brugprobleem in Koningsbergen. In Paragraaf 20 geeft Euler de drie richtlijnen die iemand kan gebruiken om erachter te komen of er een pad bestaat met behulp van elke brug één keer en slechts één keer. Ten eerste, hij beweerde dat als er meer dan twee landmassa ‘ s met een oneven aantal bruggen, dan is een dergelijke reis niet mogelijk. Ten tweede, als het aantal bruggen oneven is voor precies twee landmassa ‘s, dan is de reis mogelijk als het begint in een van de twee oneven genummerde landmassa’ s. Tot slot stelt Euler dat als er geen regio ’s zijn met een oneven aantal landmassa’ s, de reis in elke regio kan worden uitgevoerd. Na deze drie feiten te hebben uiteengezet, besluit Euler zijn bewijs met paragraaf 21, waarin eenvoudig wordt gesteld dat wanneer men ontdekt dat er een pad bestaat, men nog steeds de moeite moet nemen om een pad uit te schrijven dat werkt. Euler geloofde dat de methode om dit te bereiken triviaal was, en hij wilde er niet veel tijd aan besteden. Euler stelde echter voor zich te concentreren op hoe je van de ene landmassa naar de andere kunt komen, in plaats van je eerst te concentreren op de specifieke bruggen.

Euler ‘ s Proof and Graph Theory

bij het lezen van Eulers originele proof, ontdekt men een relatief eenvoudig en gemakkelijk te begrijpen wiskundig werk; het is echter niet het feitelijke bewijs maar de tussenliggende stappen die dit probleem beroemd maken. De grote innovatie van Euler was het abstract bekijken van het probleem van de brug van Königsberg, door lijnen en letters te gebruiken om de grotere situatie van landmassa ‘ s en bruggen weer te geven. Hij gebruikte hoofdletters om landmassa ‘ s voor te stellen, en kleine letters om bruggen voor te stellen. Dit was een volledig nieuw soort denken voor die tijd, en in zijn paper, veroorzaakte Euler per ongeluk een nieuwe tak van de wiskunde genaamd grafiettheorie, waar een grafiek gewoon een verzameling van hoekpunten en randen is. Vandaag de dag wordt een pad in een grafiek, dat elke rand van de grafiek één keer bevat, een euleriaans pad genoemd, vanwege dit probleem. Vanaf het moment dat Euler dit probleem oploste tot vandaag, is de grafentheorie een belangrijke tak van de wiskunde geworden, die de basis vormt van ons denken over netwerken. het probleem van de brug van Königsberg is waarom Biggs stelt:

De oorsprong van de grafentheorie is bescheiden, zelfs frivool … de problemen die leidden tot de ontwikkeling van de grafentheorie waren vaak weinig meer dan puzzels, ontworpen om de vindingrijkheid te testen in plaats van de verbeelding te stimuleren. Maar ondanks de schijnbare trivialiteit van dergelijke puzzels, veroverden ze de interesse van wiskundigen, met als resultaat dat de grafentheorie een onderwerp is geworden dat rijk is aan theoretische resultaten van een verrassende verscheidenheid en diepte.

zoals Biggs’ verklaring zou impliceren, is dit probleem zo belangrijk dat het wordt vermeld in het eerste hoofdstuk van elk Grafiettheorieboek dat in de bibliotheek werd gelezen.

na Eulers ontdekking (of uitvinding, afhankelijk van hoe de lezer ernaar kijkt), groeide de grafentheorie met belangrijke bijdragen van grote wiskundigen als Augustin Cauchy, William Hamilton, Arthur Cayley, Gustav Kirchhoff en George Polya. Deze mensen hebben allemaal bijgedragen aan het blootleggen van ” zowat alles wat bekend is over grote maar geordende grafieken, zoals het rooster gevormd door atomen in een kristal of het zeshoekige rooster gemaakt door bijen in een bijenkorf .”Andere bekende grafiettheoretische problemen zijn het vinden van een manier om te ontsnappen uit een doolhof of labyrint, of het vinden van de volgorde van zetten met een ridder op een schaakbord zodanig dat elk vierkant is geland op slechts een keer en de Ridder keert terug naar de ruimte waarop hij begon . Sommige andere graftheoretische problemen zijn al eeuwenlang onopgelost gebleven .

Het Lot van Königsberg

Tijdens grafiek theorie klonk na Euler opgelost de Königsberg Brug probleem, de stad Königsberg had een heel ander lot. In 1875 besloten de inwoners van Königsberg om een nieuwe brug te bouwen, tussen knooppunten B en C, waardoor het aantal verbindingen van deze twee landmassa ‘ s werd verhoogd tot vier. Dit betekende dat slechts twee landmassa ‘ s een oneven aantal verbindingen hadden, wat een vrij eenvoudige oplossing voor het probleem gaf. De creatie van de extra brug kan al dan niet onbewust zijn veroorzaakt door het verlangen naar een pad om het beroemde probleem van de stad op te lossen. een nieuwe brug Lost echter niet alle toekomstige problemen van Königsberg op, omdat de stad in de negentiende eeuw niet had verwacht dat het een triest en door oorlog verscheurd lot zou zijn dat het als gastheer voor een van de hevigste veldslagen van de Tweede Wereldoorlog zou zijn. In augustus 1944 verwoestten Britse bommenwerpers zowel de oude stad als de noordelijke delen van Königsberg. In januari en februari 1945 wordt de regio rond Königsberg omsingeld door Russische troepen. Duitse burgers beginnen te evacueren uit de stad, maar komen te laat. Duizenden mensen worden gedood door te vluchten per boot en te voet over de ijzige wateren van de Curonische lagune. In april 1945 verovert het Rode Leger Königsberg met ongeveer negentig procent van de oude stad in puin.

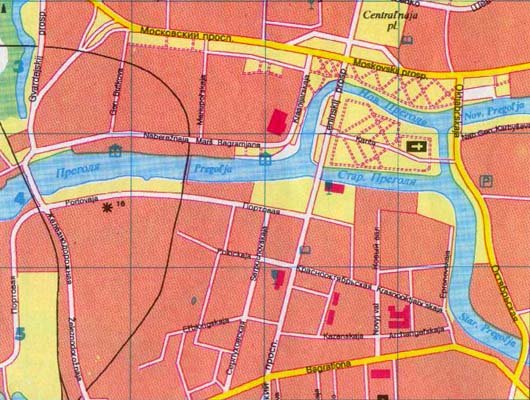
hieronder vindt u een actuele plattegrond van Königsberg . Deze kaart laat zien hoeveel de stad is veranderd. Veel van de bruggen werden vernietigd tijdens de bombardementen, en de stad kan niet meer dezelfde intrigerende vraag die ze in de achttiende eeuw konden stellen. Königsberg heeft een nieuwe naam, Kaliningrad, met de rivier de Pregel omgedoopt tot Pregolya . Terwijl het lot van Königsberg verschrikkelijk is, leidde het oude koffiehuisprobleem van de burgers om elk van hun oude zeven bruggen precies één keer te doorkruisen tot de vorming van een volledig nieuwe tak van de wiskunde, de grafentheorie.

Biggs, Norman L., E. K. Lloyd, and Robin J. Wilson. Grafentheorie: 1736-1936. Oxford: Clarendon Press, 1976.

Dunham, William. Euler: de meester van ons allemaal. Washington: The Mathematical Association of America, 1999.Euler, Leonhard, ‘Solutio problematis ad geometriam situs pertinentis’ (1741), eneström 53, Maa Euler Archive.”History of Mathematics: On Leonhard Euler (1707-1783).”ScienceWeek (2003). 6 Nov. 2005.

Hopkins, Brian, and Robin Wilson. “De waarheid over Königsberg.”College Mathematics Journal (2004), 35, 198-207.

” Konigsberg Bridges.”The MacTutor History of Mathematics Archive:
http://www-history.mcs.st- and.ac.uk/history/Miscellaneous/other_links/Konigsberg.html

Noot van de redactie: Dit artikel is oorspronkelijk gepubliceerd in Convergence, Volume 3 (2006).