9. Impedantie en fasehoek
missen niet…
onderzoek impedantie, stroom en spanning in een RLC circuit in de applet later op deze pagina.
Impedantie
De impedantie van een circuit is de totale effectieve weerstand tegen de stroomstroom door een combinatie van de elementen van het circuit.
symbool: z
eenheden: `Ω ‘
de totale spanning over alle 3 elementen (weerstanden, condensatoren en inductoren) is geschreven
VRLC
om deze totale spanning te vinden, kunnen we niet gewoon de spanningen VR, VL en VC optellen.
omdat VL en VC als imaginaire grootheden worden beschouwd, hebben we:
impedantie VRLC = IZ
So `Z = R + j(X_L− X_C)`
nu wordt de magnitude (grootte, of absolute waarde) van z gegeven door:
`|Z/=sqrt(R^2+(X_L-X_C)^2`
fasehoek
`tan\ theta=(X_L-X_C)/R`
hoek θ vertegenwoordigt de fasehoek tussen de stroom en de spanning.
vergelijk dit met de fasehoek die we eerder tegenkwamen in grafieken van y = a sin (bx + c).
Voorbeeld 1
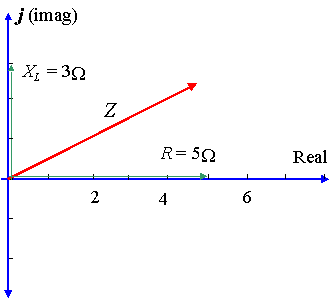
een circuit heeft een weerstand van` 5\ Ω `in serie met een reactantie over een inductor van`3\ Ω’. Stel de impedantie voor door een complex getal, in polaire vorm.
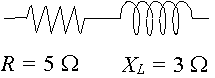
antwoord
In dit geval, `x_l= 3\ ω` en `x_c= 0` dus `x_l – x_c= 3\ ω`.
in rechthoekige vorm wordt de impedantie geschreven:
`Z = 5 + 3j\ Ω`
met behulp van een rekenmachine wordt de magnitude van Z gegeven door: `5.83`, en de hoek `θ` (het faseverschil) wordt gegeven door: `30.96^@`.
dus de spanning leidt de stroom met `30.(`) Zie diagram.
presenterend als een complex getal (in polaire vorm), hebben we:
`Z = 5,83 30 30,96^@\ Ω`.
Voorbeeld 2(a)
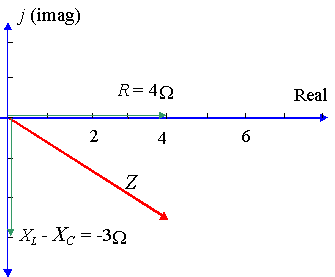
een bepaalde wisselstroomkring heeft een weerstand van `4\ Ω`, een reactantie over een inductor van `8\ Ω` en een reactantie over een condensator van `11\ Ω`. Druk de impedantie van het circuit uit als een complex getal in polaire vorm.
antwoord
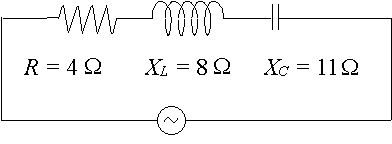
In dit geval hebben we: `X_L – X_C= 8 – 11 = -3\ Ω`
So `Z = 4 – 3j\ ω` in rechthoekige vorm.
om het nu in polaire vorm uit te drukken:
met behulp van een rekenmachine vinden we `r = 5` en ` θ = -36.87^@`.
So `Z = 5 ∠ -36.87^@\ Ω`
interactieve RLC grafiek
Hieronder is een interactieve grafiek om mee te spelen (het is geen statische afbeelding). U kunt het effect van een weerstand, condensator en inductor op de totale impedantie in een wisselstroomcircuit onderzoeken.
activiteiten voor deze interactieve
- speel eerst met de schuifregelaars. U kunt:
sleep de bovenste schuifregelaar naar links of rechts om de impedantie door de weerstand te variëren, `R`,
sleep de XL schuifregelaar omhoog of omlaag om de impedantie door de inductor te variëren, `X_L`, en
sleep de XC schuifregelaar omhoog of omlaag om de impedantie door de condensator te variëren, `X_C`. - observeer de effecten van verschillende impedanties op de waarden van XL-XC en Z.
- observeer de effecten van verschillende impedanties op θ, de hoek die de rode “resultaat” lijn maakt met de horizontale (in radialen).
- overweeg de grafieken van spanning en stroom in de interactieve. Let op de hoeveelheid vertraging of lood als u de schuifregelaars te veranderen.
- Wat heb je geleerd van het spelen met deze interactieve?