2.5: Darcy’ s Law – Flow in a Porous Medium
Darcy ‘ s law is cruciaal voor het begrijpen van vele takken van de geologie, met name hydrogeologie. Voordat we kijken naar de wet en wat het ons kan vertellen, laten we kijken naar hoe het is ontwikkeld. De wet van Darcy is vernoemd naar Henry Darcy, een 19e-eeuwse Franse ingenieur die een ondergronds leidingsysteem onder druk ontwikkelde om water te leveren rond de stad Dijon. Het systeem, dat ook water leverde aan de beroemde Dijon fonteinen, revolutioneerde stad water en riolering systemen. Het systeem had geen pompen nodig en werd puur door de zwaartekracht aangedreven. Tijdens het proces van de ontwikkeling van het nieuwe systeem, Darcy voerde een reeks experimenten waar hij probeerde om water te verplaatsen uitsluitend met behulp van zwaartekracht.
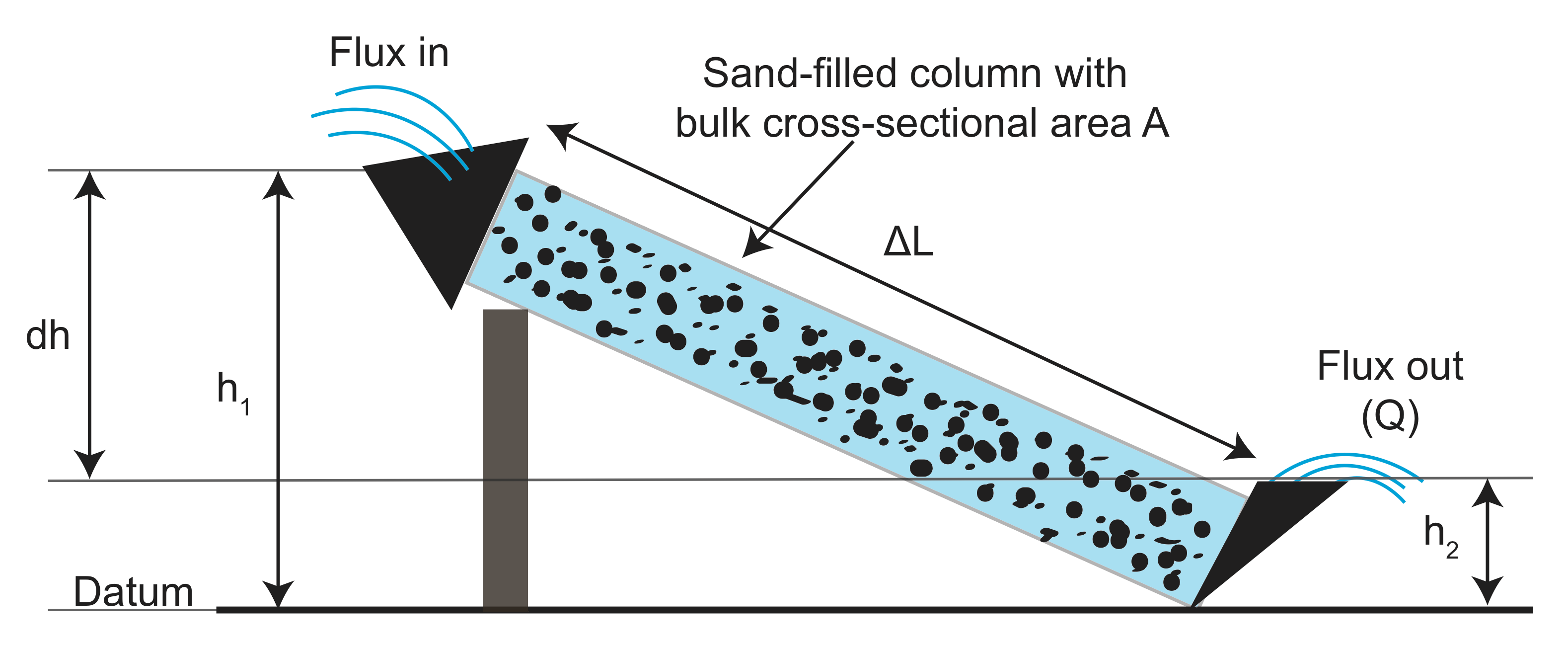
uit de experimenten, verzamelde gegevens over de lengte van de goot (\(L\)), de doorsnede van de goot (\(A\)), het hoogteverschil (\(h_1 – h_2\)), en de flux van water die \(Q\) zowel met als zonder korrelig (filtering) materiaal in de goot. Vervolgens zette hij de flux meting genormaliseerd door het gebied versus de verhouding van het hoogteverschil tot de lengte van de goot (\( \frac{h_1 – h_2}{l}\)). Wat hij ontdekte is dat er een lineair verband is, en de helling hangt af van het korrelige materiaal dat hij in de goot gebruikte:
\
die als afgeleide kan worden herschreven,
\
waarin \(K\) de hydraulische geleidbaarheid is en \(\frac{dh}{dx}\) de hydraulische gradiënt is. \(Q\), de totale afvoersnelheid, heeft eenheden van \(\frac{m^3}{s}\), het volume water per keer. Het negatieve teken is te wijten aan het feit dat de vloeistof naar beneden (negatief) de hydraulische gradiënt van hogere waarden naar lagere waarden.
De hydraulische geleidbaarheid is een fysische parameter die aangeeft hoe gemakkelijk de vloeistof door de porieruimte van het materiaal kan bewegen. In Darcy ‘ s originele experimenten gebruikte hij zand met verschillende korrelgroottes, maar de hydraulische geleidbaarheid kan ook worden bepaald voor vaste rotsen, omdat de meeste rotsen wat porieruimte hebben.in navolging van Darcy ‘ s originele experimenten werd verder onderzoek gedaan naar de fysische eigenschappen van de vloeistof en het gesteente die de effectieve hydraulische geleidbaarheid bepalen. Uit deze experimenten bleek dat
\
waarin \(k\) de intrinsieke permeabiliteit van het poreuze medium (de vaste stof) is, \(\eta\) de dynamische viscositeit van de vloeistof is, en \(\gamma = \rho g\) het soortelijk gewicht van de vloeistof is, dat afhankelijk is van de Vloeistofdichtheid, \(\rho\) en zwaartekracht, \(g\).
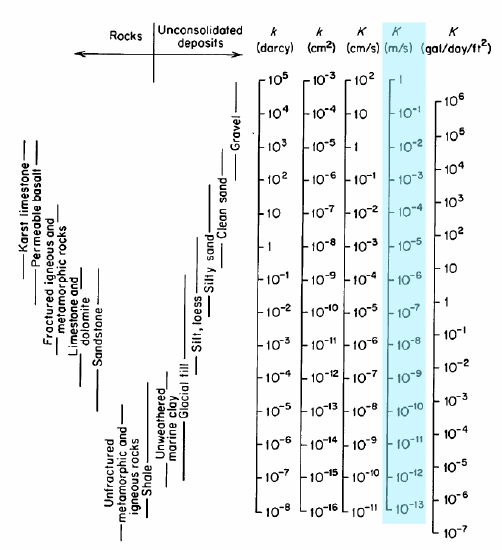
de gemarkeerde kolom in de figuur is K, de hydraulische geleidbaarheid in \(\frac{m}{s}\); Dit zijn de eenheden die we gaan gebruiken. De hydraulische geleidbaarheid wordt soms ook gerapporteerd in termen van de intrinsieke permeabiliteit, \(k\), met eenheden van Darcy ‘ s of cm2. Het volledige bereik van waarden voor hydraulische geleidbaarheid is 1-10-13 \(\frac{m}{s}\). Experimenten zoals Darcy ‘ s worden gebruikt om K te meten in echte materialen.
De lozingen \Q\) is een volume flux (\(m^3/s\)), maar we denken meestal van de stroming in termen van snelheid of de snelheid. De ontladingsvragen kunnen worden herschikt door door het gebied te delen om de Darcy Flux
\ \]
te definiëren of in termen van de intrinsieke permeabiliteit en drukgradiënt,
\
waarin \(\eta\) de vloeibare viscositeit is (zie hieronder voor de afleiding van de tweede vergelijking).
Het is belangrijk op te merken dat Darcy flux niet gelijk is aan de vloeistofsnelheid, ook al is het in eenheden van snelheid. De vloeistofsnelheid wordt gevonden door de gemiddelde lineaire snelheid (\(v_a\)), die het gemiddelde is van de snelheid van alle mogelijke vloeistofbanen door de poreuze media: maar het vinden van deze waarde valt buiten het bereik van deze klasse. In plaats daarvan zullen we opmerken dat de vloeistofsnelheid
\
is waarbij \(\varphi\) de porositeit is en v de vloeistofsnelheid. De porositeit, \(\varphi\) wordt berekend als de verhouding van het volume van de lege ruimte tot het totale volume van een materiaal \(\varphi=\frac{V_{void}}{V_{tot}}\), en wordt meestal uitgedrukt als een breuk tussen 0 en 1 of als een percentage. Merk op dat als \(\varphi\leq\)1 dan de vloeistofsnelheid groter is dan de darcy flux.
een andere term die ontstaat bij het bespreken van stroom door rotsen en niet-geconsolideerde materialen is permeabiliteit. Hoewel porositeit de werkelijke fractie van poriën (holtes) in de rots is, kunnen deze holtes verschillende vormen en verschillende connectiviteit hebben, wat van invloed is op hoe gemakkelijk een vloeistof door de porieruimte kan bewegen. De permeabiliteit is een maat voor het gemak waarmee vloeistoffen en gassen door een rots kunnen gaan. Hoe meer geconsolideerd het materiaal, hoe lager de permeabiliteit. Dus “losse” materialen zoals grind hebben een hoge permeabiliteit. Sommige rotsen kunnen ook anisotrope permeabiliteit hebben, wat betekent dat vloeistoffen gemakkelijk in de ene richting kunnen stromen, maar niet in de andere. Een voorbeeld van een rots met anisotrope permeabiliteit is een leisteen. Vloeistoffen kunnen gemakkelijk binnen een laag van de leisteen bewegen, maar kunnen niet over lagen bewegen.
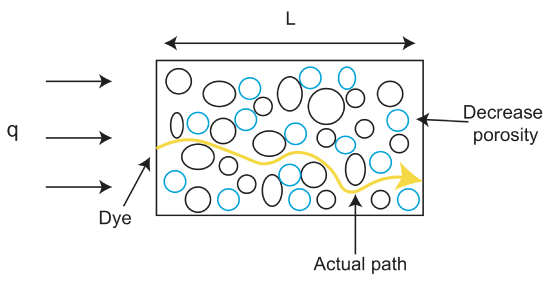
Fluid Velocity
laten we een basisvoorbeeld doen.
we krijgen dat \(q = 2 \ frac{m}{min}\) en \(\varphi\) 25% is en de vloeistofsnelheid willen vinden.
we converteren eerst 25% naar 0.25.
dan, \(v = \frac{2}{0.25}\frac{m}{min}\)
en
\(v=8 \frac{m}{min}\) is de vloeistofsnelheid.
hydraulische leiding
terugkerend naar Darcy ‘ s experimenten, Wat is het fysieke proces eigenlijk drijft de stroom van vloeistof door de goot?
De term \(\frac{dh}{dx} \) wordt aangeduid als de hydraulische kop, die de vloeistofdruk is als gevolg van het gewicht van een vloeistof ten opzichte van een referentieplaats: een drukgradiënt. Echter, \(\frac{dh}{dx} \) heeft geen eenheden van een druk per lengte-eenheid, dus waarom wordt het de hydraulische kop genoemd?
laten we eens kijken wat de druk is in de goot in Darcy ‘ s experimenten. Om de experimenten te doen, Darcy ‘ s had een tank van water aan de bovenkant van de goot die een constant niveau van water aan de bovenkant van de goot, gelijk aan de hoogte van de goot, \(h_1\). Op dezelfde manier was er een tank aan de onderkant met een constant waterniveau gelijk aan \(h_2\). Daarom wordt de vloeistofdruk in elk van de tanks als gevolg van het gewicht van het water gegeven door \(P = \rho g h\). De drukgradiënt tussen de boven-en onderkant van de Pluim is dan
\
of
\
vervangt de wet van Darcy,
\ &=\frac{K}{\rho g}\frac{dp}{dx} \end{align}. \ ]
bedenk, van bovenaf, dat de hydraulische geleidbaarheid kan worden geschreven in termen van de intrinsieke permeabiliteit als \(K = k\frac{\gamma}{\eta}\) wat gelijk is aan \(k\frac{\rho g}{\eta} \) of herschikken, \(\frac{K}{\rho g} = \frac{k}{\eta} \). Daarom kunnen we twee equivalente uitdrukkingen voor Darcy ’s wet vervangen, met één interms van de gradiënt in hoogte,
en de tweede in termen van de gradiënt in druk,
\
dus,\(\frac{dh}{dx}\) wordt de hydraulische kop genoemd omdat de fysische oorsprong van de term in Darcy’ s wet de drukgradiënt in de vloeistof is, die de stroom drijft.
Water dat een Aquifer verlaat
laten we nu een voorbeeld geven voor het berekenen van de vloeistofsnelheid van water dat een aquifer binnenkomt. In de schets Hieronder volgt de hoogte van de aquifer de topografie op de heuvel naast de vallei met de Beek. Water stroomt van hoge druk (hoofdhoogte) naar de vallei en verlaat de aquifer bij de Beek. We kunnen Darcy ‘ s Wet gebruiken om de waterstroom van de aquifer te schatten.
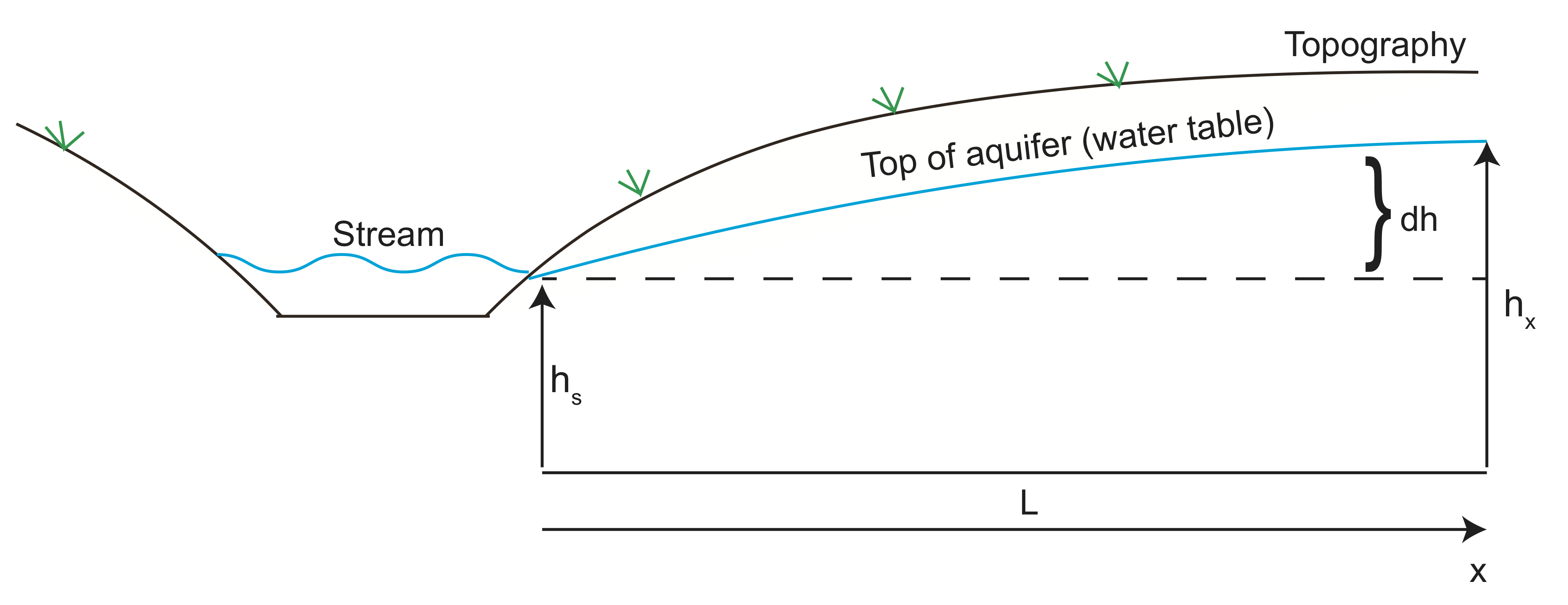
met behulp van geofysische beeldvorming blijkt de hoogte van de aquifer 10 m (\(dh\)) boven de stroomhoogte ongeveer 100 meter (\(L\)) verwijderd te zijn. Stel dat de hydraulische geleidbaarheid \( K=10^{-6}\) m/s is en de porositeit \(\varphi=30\)%.
De darcy flux is
\
\
de vloeistofsnelheid is
\
\
\
\
\

laminaire versus turbulente stroom
een van de impliciete veronderstellingen in Darcy ‘ s wet is dat de stroom laminaire is. Laminaire stroming wordt gekenmerkt als bestaande uit dunne lagen of laminae van vloeistof die allemaal parallel aan elkaar bewegen. Turbulente stroming wordt daarentegen gekenmerkt door wervelingen, wervelingen en wervelingen, waarbij aangrenzende lagen van vloeistof uiteenlopen en verschillende paden langs de stroom nemen.
een manier om te kwantificeren of een vloeistof laminair of turbulent is, is door het getal van Reynold voor de stroom te berekenen, gedefinieerd als
het getal van Reynold wordt gevonden door de twee termen in de momentumbalans voor de stroom te beschouwen. De eerste term is de traagheidskracht per volume-eenheid, die de stroom drijft, \(\rho u \ frac{du}{dx}\). De tweede term is de viskeuze kracht per volume-eenheid, die flow weerstaat, \(\eta \ frac{d^2u}{dx^2}\). Deze twee termen moeten balanceren, zodat we ze gelijk kunnen stellen,
\
vervolgens herschrijven we de termen, op een vereenvoudigde manier om alleen de relevante dimensies van de variabelen vast te leggen. Om dit te doen, gaan we door wat een dimensionale analyse wordt genoemd, waarin we elke variabele vervangen, door een referentiewaarden, maal een niet-dimensionale vorm van de variabele.
bijvoorbeeld voor de term \(x\) wordt herschreven als gewoon \(L x’\), waarbij \(L\) de referentielengte is (de vloeistofdiepte) en \(x’\) de niet-dimensionale afstand is. Evenzo laten we \(u = u_o u’\). Door deze in de vergelijking te vervangen krijgen we
\
vervolgens combineren we de constante waarden vooraan
\
merk op dat de combinatie van variabelen vooraan het Reynold ‘ s nummer
\
is waarbij de variabelen \(u_o\) stroomsnelheid, l vloeistofdiepte, en de variabelen die we eerder gezien hebben, \(\rho\) Vloeistofdichtheid, en \(\eta\) vloeistofviscositeit zijn. Door het doorlopen van deze analyse, vinden we dat elke stroom die wordt gekenmerkt door de balans van deze twee termen kan worden vergeleken door simpelweg het kennen van de waarde van het getal van Reynolds. Bijvoorbeeld, als een stroom heeft een viscositeit die 10 keer de viscositeit in een andere stroom, de twee stromen zal gedragen hetzelfde is de dichtheid (of snelheid of lengte) wordt ook verhoogd met een factor 10 voor de hogere viscositeit geval; dat wil zeggen, het getal Reynolds voor de twee stromen is hetzelfde.
om Darcy te laten stromen, moet het getal van Reynold kleiner zijn dan ongeveer 1-10 (laminair). Voor \(Re>1-10 \) is de stroom niet strikt laminair, maar nog niet turbulent (niet-lineair, niet-laminair). Om turbulente stroming te hebben, moet het aantal Reynold groter zijn dan ongeveer 2000.
begrijpen dat de constanten in de teller en noemer de eigenschappen van de stroom op de tegenovergestelde manier beïnvloeden, helpen ook om na te denken over hoe verschillende vloeistoffen zich zullen gedragen onder vergelijkbare externe omstandigheden. Bijvoorbeeld, zal een dichtere vloeistof die ook een snelle snelheid heeft een hogere Re hebben en turbulent gedrag vertonen. Daarentegen zal een vloeistof zoals ijs die een hoge viscositeit heeft en zeer langzaam beweegt een lage Re hebben en waarschijnlijk laminaire stroming hebben. De hoge viscositeit van het ijs werkt om de stroming te stabiliseren. Als een ander voorbeeld, beschouw twee vloeistoffen kunnen beide bewegen met dezelfde snelheid zich anders gedragen als de andere waarden in het Reynold ‘ s nummer \(\frac {\rho L}{\mu}\) verschillend zijn. Daarom hangt het stromingstype niet alleen af van de stromingssnelheid, maar ook van de combinatie van variabelen in het Reynold ‘ s getal.
toepassing van Darcy ’s Flow
Darcy’ s law is de belangrijkste vergelijking die de flow in aquifers en putten regelt. Zonder dat, zouden we niet in staat zijn om putten te boren of te begrijpen water beweging in aquifers, vooral in Californië central valley, waar beide ideeën zijn cruciaal voor zowel de landbouw productiviteit en grondwaterdaling.
