i denne opplæringen vil vi lære Om Wheatstone Bridge. Vi vil se Arbeidsprinsippet Til Wheatstone Bridge, få eksempelkretser og noen viktige applikasjoner.

Introduksjon Til Wheatstone Bridge

i den virkelige verden kommer vi over ulike signaler, noen av dem måles ved endringer i motstand og noen av dem er med induktans og kapasitans.

hvis vi vurderer motstanden, vil de fleste industrielle sensorer som temperatur, belastning, fuktighet, forskyvning, væskenivå, etc. produserer endringen i verdien av motstanden for en variabel endring. Derfor er det behov for en signalkondisjonering for hver motstandssensor.generelt er motstandsmålingen delt inn i tre typer, lav motstandsmåling, middels motstandsmåling og høy motstandsmåling. Hvis motstandsmålingen muligens er fra noen få milliohm til mikro ohm, betraktes det som en lav motstandsmåling.

denne målingen brukes faktisk til forskningsformål. Hvis målingen er fra 1 ohm til 100 k er generelt referert til som en middels motstandsmåling. Potensiometer, termistorer, etc. måling kommer under denne kategorien.

og meget høy motstandsmåling regnes fra 100 kilo ohm til større enn 100 mega ohm. For å finne mediumverdien av motstanden brukes forskjellige metoder, men det meste Brukes Wheatstone bridge.

Hva Er Wheatstone Bridge?

DET vanligste og enkleste bronettet for å finne motstanden er DC Wheatstone Bridge. Denne broen brukes der små endringer i motstand skal måles som i sensorapplikasjoner. Dette brukes til å konvertere en motstandsendring til en spenningsendring av en svinger.kombinasjonen av denne broen med operasjonsforsterker brukes mye i bransjer for ulike transdusere og sensorer. En Wheatstone bro bestar av fire motstander som er koblet i form av en diamant med forsyningskilden og angir instrumenter som vist i fig.

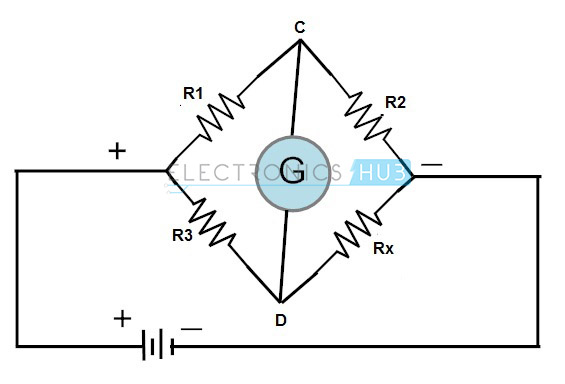
denne broen brukes til å finne den ukjente motstanden veldig nøyaktig ved å sammenligne den med en kjent verdi av motstander. I denne broen brukes null eller balansert tilstand til å finne motstanden.

for denne brobalanserte tilstanden må spenningen Ved punktene C og D være lik. Derfor strømmer ingen strøm gjennom galvanometeret. For å få balansert tilstand må en av motstandene være variabel.

From the figure,

The voltage at point D = V × RX / (R3 + RX)

The voltage at point C = V × R2 / (R1 + R2)

The voltage (V) across galvanometer or between C and D is,

VCD = V × RX / (R3 + RX) − V R2 / (R1 + R2)

When the bridge is balanced VCD = 0,

So,

V × RX / (R3 + RX) = V R2 / (R1 + R2)

RXR1 + RXR2 = R2R3 + R2RX

R1RX= R2R3

R2/R1= RX/R3

This er betingelsen for å balansere broen. Og for å finne den ukjente verdien av motstand

RX = R3 × (R2 / R1)

Fra ovennevnte ligning R4 eller Rx kan beregnes ut fra den kjente verdien av motstand R3 Og forholdet R2/R1. Derfor er de fleste tilfeller r2 og R1 verdier fast Og r3-verdien er variabel slik at nullverdien oppnås og broen blir balansert.

Arbeidsprinsipp

uten galvanometeret ser brokretsen bare ut som en spenningsdelerkrets som vist på figuren nedenfor. Vurder R1 = 20 ohm, R2= 40 ohm for en arm og for den andre vurdere samme verdier av henholdsvis r3 og r4.

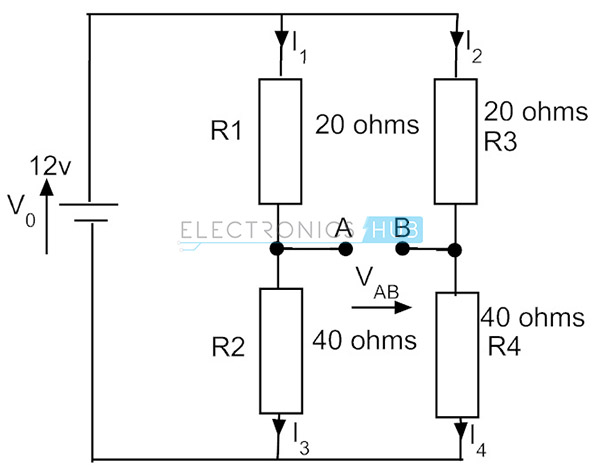
strømmen i første arm er

I1 = v/(R1+R2)

i1 = 12v/(20+40)

I1 = 0.2 a

og spenningen ved punkt c er lik spenningsfallet ved motstanden R2,

vr2 = i1 × r2= 0,2 × 40 = 8v

på samme måte er spenningen over r1 4v (0,2 × 20). På grunn av de samme motstandsverdiene vil spenningene Ved R4 og R3 være de samme som For henholdsvis r1 og R2. Derfor er punktene A og B spenninger samme, derfor viser galvanometeret nullavlesning da potensiell forskjell er null. I dette tilfellet sies broen å være i balansert tilstand.

Anta at hvis vi reverserer motstandene i den andre armen, er strømmen den samme på grunn av seriekretsen. Men spenningen over motstanden r4 endres, dvs. 0,2 * 20 = 4V. Så ved denne tilstanden er spenningen over punktene A og B forskjellige og eksisterer en potensiell forskjell på 8 – 4 = 4v. Dette er broens ubalanserte tilstand.

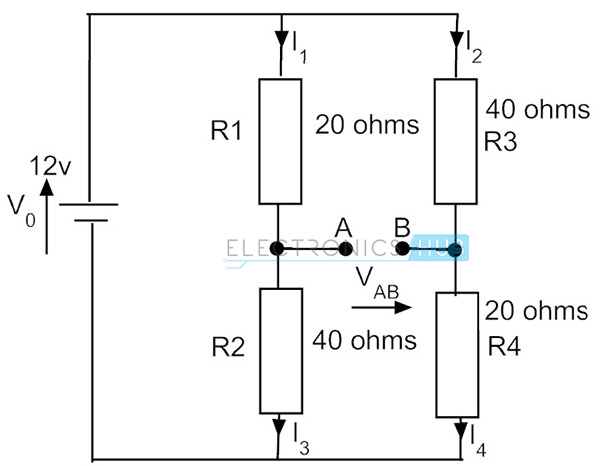
Eksempel På Wheatstone Bridge

fra oven er Wheatstone-broen ubalansert når voltmeteravlesningen ikke er null. Denne avlesningen kan være positiv eller negativ, avhenger av størrelsen på spenningene på målerterminalene. La oss se på den under kretsen Av Wheatstone bridge som er koblet til å finne den ukjente motstandsverdien ved bruk av motstand tiår boks for å få den variable motstanden Til R3.

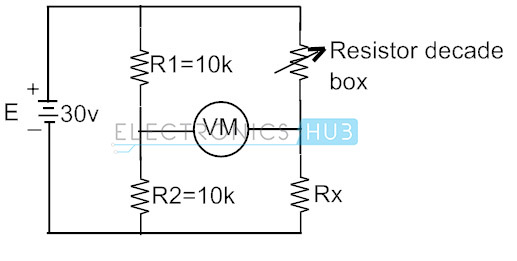
vi vet at betingelsen for bro balanse er

R4 = R3 × R2 / R1

rx = rbox × (10 x 103)/ (10 x 103)

rx = rbox

her i dette tilfellet balanseres wheatstone-broen ved å justere tiårsmotstandsboksen til voltmeteret leser nullverdi. Og den tilsvarende motstandsverdien i boksen er lik den ukjente motstanden. Anta at hvis spenningsnulltilstanden oppstår ved 250 ohm av motstandsboksen, er den ukjente motstanden også 250 ohm.

Wheatstone Bro For Belastningsmåling

vanligvis for måling av belastningen, brukes belastningsmålere hvis elektrisk motstand varierer med forholdsmessig belastning i enheten. I praksis er rekkevidden av spenningsmålermotstand fra 30 ohm til 3000 ohm. For en gitt belastning kan motstandsendringen bare være en brøkdel av hele spekteret. Derfor, for å måle ekstremt en brøkdel av motstandsendringer med høy nøyaktighet, Brukes Wheatstone brokonfigurasjon. Figuren nedenfor viser Wheatstone-broen hvor den ukjente motstanden er erstattet med en spenningsmåler.

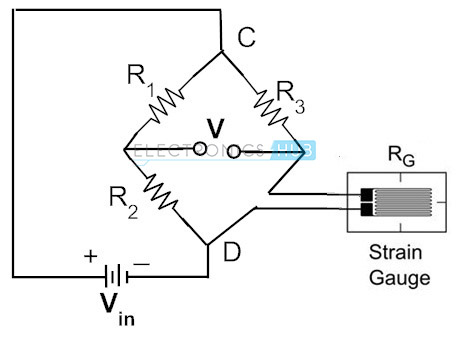
i den ovennevnte kretsen er to motstander R1 Og R2 lik hverandre og R3 er den variable motstanden. Med ingen kraft påført spenningsmåleren, er rheostat variert og endelig plassert slik at voltmeteret vil indikere null avbøyning. Dette kalles en bro balansering tilstand. Denne tilstanden representerer at det ikke er noen belastning på måleren.

hvis spenningsmåleren enten er spent eller komprimert, kan motstanden øke eller redusere. Derfor forårsaker dette ubalanse av broen. Dette gir en spenningsindikasjon pa voltmeter som tilsvarer belastningsendringen. Hvis belastningen på en spenningsmåler er mer, er spenningsforskjellen over målerterminalene mer. Hvis belastningen er null, så broen balanserer og meter viser null lesing.

dette handler om motstandsmåling ved hjelp Av En Wheatstone bro for nøyaktig måling. På grunn av brøk måling av motstand, Wheatstone broer er mest brukt i strain gauge og termometer målinger.

Applikasjoner

1. Wheatstone-broen brukes til å måle de svært lave motstandsverdiene nøyaktig.Wheatstone bridge sammen med operasjonsforsterker brukes til å måle de fysiske parametrene som temperatur,belastning, lys, etc.
2. Vi kan også måle mengder kapasitans, induktans og impedans ved hjelp av variasjonene På Wheatstone-broen.