Regresjon til gjennomsnittet er et vanlig statistisk fenomen som kan villede oss når vi observerer verden. Å lære å gjenkjenne når regresjon til gjennomsnittet er på spill, kan hjelpe oss med å unngå å feiltolke data og se mønstre som ikke eksisterer.

***

Det er viktig å minimere tilfeller av dårlig dømmekraft og ta opp de svake punktene i vår resonnement. Lære om regresjon til gjennomsnittet kan hjelpe oss.den Nobelprisvinnende psykologen Daniel Kahneman skrev en bok om skjevheter som overskygger vårt resonnement og forvrenger vår oppfatning av virkeligheten. Det viser seg at det er et helt sett logiske feil som vi begår fordi vår intuisjon og hjerner ikke går bra med enkel statistikk. En av feilene han undersøker I Å Tenke Fort Og Sakte er den beryktede regresjonen mot gjennomsnittet.begrepet regresjon til gjennomsnittet ble først utarbeidet Av Sir Francis Galton. Regelen sier at i alle serier med komplekse fenomener som er avhengige av mange variabler, hvor sjansen er involvert, har ekstreme utfall en tendens til å bli etterfulgt av mer moderate.

Ved Å Søke Visdom, Tilbyr Peter Bevelin eksemplet På John, som var misfornøyd med ytelsen til nye ansatte, så han satte dem inn i et ferdighetsforbedrende program hvor han målte de ansattes ferdigheter:

deres score er nå høyere enn de var på den første testen. Johns konklusjon: «det ferdighetsforbedrende programmet forårsaket forbedringen i ferdigheter.»Dette er ikke nødvendigvis sant. Deres høyere score kan være et resultat av regresjon til gjennomsnittet. Siden disse personene ble målt som å være på den lave enden av ferdighetsskalaen, ville de ha vist en forbedring selv om de ikke hadde tatt ferdighetsforbedrende programmet. Og det kan være mange grunner til deres tidligere ytelse — stress, tretthet, sykdom, distraksjon, etc. Deres sanne evne har kanskje ikke endret seg.

vår ytelse varierer alltid rundt noen gjennomsnittlig sann ytelse. Ekstrem ytelse har en tendens til å bli mindre ekstrem neste gang. Hvorfor? Testmålinger kan aldri være nøyaktige. Alle målinger består av en sann del og en tilfeldig feildel. Når målingene er ekstreme, er de sannsynligvis delvis forårsaket av en tilfeldighet. Sjansen er sannsynlig å bidra mindre på andre gang vi måler ytelse.hvis vi bytter fra en måte å gjøre noe på til en annen bare fordi vi ikke lykkes, er det svært sannsynlig at vi gjør det bedre neste gang, selv om den nye måten å gjøre noe på er lik eller verre.

dette er en av grunnene til at det er farlig å ekstrapolere fra små utvalgsstørrelser, da dataene kanskje ikke er representative for distribusjonen. Det er også Grunnen Til At James March hevder at jo lenger noen forblir i jobben sin, » jo mindre er den sannsynlige forskjellen mellom den observerte oversikten over ytelse og faktisk evne.»Alt kan skje på kort sikt, spesielt i enhver innsats som innebærer en kombinasjon av dyktighet og flaks. (Forholdet mellom ferdighet og flaks påvirker også regresjon til gjennomsnittet.)

Regresjon til Gjennomsnittet

effektene av regresjon til gjennomsnittet kan ofte observeres i sport, hvor effekten forårsaker mange uberettigede spekulasjoner.I Thinking Fast And Slow husker Kahneman å se på menns hopp, en disiplin hvor sluttresultatet er en kombinasjon av to separate hopp. Klar over regresjonen til gjennomsnittet, Ble Kahneman skremt for å høre kommentatorens spådommer om det andre hoppet. Han skriver:

Norge hadde et flott første hopp; Han vil være spent, håper å beskytte sin ledelse og vil trolig gjøre verre» Eller «Sverige hadde et dårlig første hopp og nå vet han at han ikke har noe å tape og vil være avslappet, noe som skal hjelpe ham til å gjøre det bedre.

Kahneman påpeker at kommentatoren hadde lagt merke til regresjonen til gjennomsnittet og kommet opp med en historie som det ikke var årsakssammenheng for (se fortellende feil). Dette er ikke å si at hans historie ikke kunne være sant. Kanskje, hvis vi målte hjertefrekvensen før hvert hopp, ville vi se at de er mer avslappet hvis det første hoppet var dårlig. Men det er ikke poenget. Poenget er at regresjon til gjennomsnittet skjer når flaks spiller en rolle, som det gjorde i utfallet av det første hoppet.

leksjonen fra sport gjelder for enhver aktivitet hvor sjanse spiller en rolle. Vi legger ofte forklaringer på vår innflytelse over en bestemt prosess til fremdriften eller mangelen på den.i virkeligheten er vitenskapen om ytelse kompleks, situasjonsavhengig og ofte er mye av det vi tror er innenfor vår kontroll, virkelig tilfeldig.

ved hopp, vil en sterk vind mot jumperen føre til at selv den beste idrettsutøveren viser middelmådige resultater. På samme måte kan en sterk vind og skiforhold til fordel for en middelmådig jumper føre til en betydelig, men en midlertidig støt i hans resultater. Disse effektene vil imidlertid forsvinne når forholdene endres, og resultatene vil gå tilbake til det normale.

Dette kan ha alvorlige implikasjoner for coaching og prestasjonssporing. Regresjonsreglene tyder på at når vi vurderer ytelse eller ansettelse, må vi stole på mer enn utfall av bestemte situasjoner. Ellers er vi tilbøyelige til å bli skuffet.Da Kahneman holdt Et foredrag For Det Israelske Flyvåpenet om psykologien bak effektiv trening, delte en av offiserene sin erfaring med at det å gi ros til sine underordnede førte til dårligere prestasjoner, mens det å kjefte førte til en forbedring i de påfølgende anstrengelsene. Som en konsekvens, han hadde vokst til å være sjenerøs med negative tilbakemeldinger og hadde blitt ganske skeptisk til å gi for mye ros.

Kahneman oppdaget umiddelbart at det var regresjon til gjennomsnittet på jobben. Han illustrerte misforståelsen ved en enkel øvelse du kanskje vil prøve deg selv. Han tegnet en sirkel på en tavle og spurte offiserene en etter en om å kaste et stykke kritt i midten av sirkelen med ryggen mot tavlen. Han gjentok eksperimentet og registrerte hver offiseres ytelse i første og andre forsøk.Naturligvis hadde De som gjorde det utrolig bra på første forsøk en tendens til å gjøre det verre på sitt andre forsøk og omvendt. Feilen ble umiddelbart klar: endringen i ytelse skjer naturlig. Det igjen er ikke å si at tilbakemelding ikke betyr noe i det hele tatt-kanskje det gjør det, men offiseren hadde ingen bevis for å konkludere med at det gjorde.

Den Ufullkomne Korrelasjonen og Sjansen

På dette punktet lurer du kanskje på hvorfor regresjonen til gjennomsnittet skjer og hvordan vi kan sørge for at vi er klar over det når det skjer.

for å forstå regresjon til gjennomsnittet må vi først forstå korrelasjon.

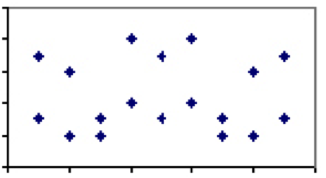
korrelasjonskoeffisienten mellom to mål som varierer mellom -1 og 1, er et mål på den relative vekten av faktorene de deler. For eksempel, to fenomener med få faktorer delt, slik som flaskevann forbruk versus selvmordsrate, bør ha en korrelasjonskoeffisient på nær 0. Det vil si, hvis vi så på alle land i verden og plottet selvmordsrater av et bestemt år mot forbruk av flaskevann per innbygger, ville plottet ikke vise noe mønster i det hele tatt.

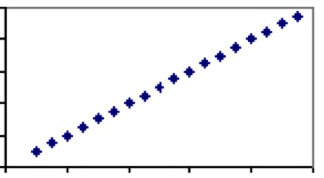
tvert imot er det tiltak som utelukkende er avhengige av samme faktor. Et godt eksempel på dette er temperatur. Den eneste faktoren som bestemmer temperatur – hastighet av molekyler-deles av alle skalaer, derfor vil hver Grad I Celsius ha nøyaktig en tilsvarende verdi I Fahrenheit. Derfor vil temperaturen I Celsius og Fahrenheit ha en korrelasjonskoeffisient på 1 og plottet vil være en rett linje.

det er få om noen fenomener i humanvitenskap som har en korrelasjonskoeffisient på 1. Det er imidlertid mange hvor foreningen er svak til moderat, og det er noen forklaringskraft mellom de to fenomenene. Vurder sammenhengen mellom høyde og vekt, som vil lande et sted mellom 0 og 1. Mens nesten hver treåring vil være lettere og kortere enn hver voksen mann, vil ikke alle voksne menn eller treårige av samme høyde veie det samme.

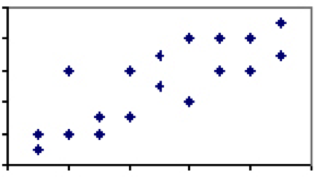
denne variasjonen og tilsvarende lavere grad av korrelasjon innebærer at mens høyden generelt sett er en god prediktor, er det tydelig andre faktorer enn høyden som spiller inn. Når korrelasjonen mellom to tiltak er mindre enn perfekt, må vi passe på effektene av regresjon til gjennomsnittet.

Kahneman observert en generell regel: Når korrelasjonen mellom to score er ufullkommen, vil det være regresjon til gjennomsnittet.

Dette kan i begynnelsen virke forvirrende og ikke veldig intuitivt, men graden av regresjon til gjennomsnittet er direkte relatert til graden av korrelasjon av variablene. Denne effekten kan illustreres med et enkelt eksempel.Anta at du er på en fest og spør hvorfor det er at svært intelligente kvinner har en tendens til å gifte seg med menn som er mindre intelligente enn de er. De fleste, selv de med litt trening i statistikk, vil raskt hoppe inn med en rekke årsaksforklaringer som spenner fra å unngå konkurranse til frykten for ensomhet som disse kvinnene står overfor. Et tema for en slik kontrovers er sannsynlig å hisse opp en stor debatt.Nå, hva om vi spurte hvorfor sammenhengen mellom intelligenspoengene til ektefeller er mindre enn perfekt? Dette spørsmålet er neppe så interessant, og det er lite å gjette – vi vet alle at dette er sant. Paradokset ligger i det faktum at de to spørsmålene tilfeldigvis er algebraisk ekvivalente. Kahneman forklarer:

hvis korrelasjonen mellom ektefellens intelligens er mindre enn perfekt (og hvis menn og kvinner i gjennomsnitt ikke er forskjellige i intelligens), så er det en matematisk uunngåelighet at svært intelligente kvinner vil bli gift med ektemenn som i gjennomsnitt er mindre intelligente enn de er (og omvendt, selvfølgelig). Den observerte regresjonen til gjennomsnittet kan ikke være mer interessant eller mer forklarlig enn den ufullkomne korrelasjonen.

Forutsatt at korrelasjonen er ufullkommen, er sjansene for to partnere som representerer topp 1% i form av noen karakteristikk langt mindre enn en partner som representerer topp 1% og den andre – bunnen 99%.

Årsaken, Effekten og Behandlingen

vi bør være spesielt forsiktige med regresjonen til det gjennomsnittlige fenomenet når vi prøver å etablere årsakssammenheng mellom to faktorer. Når korrelasjonen er ufullkommen, vil det beste alltid synes å bli verre, og det verste ser ut til å bli bedre over tid, uavhengig av ytterligere behandling. Dette er noe som de generelle media og noen ganger til og med trente forskere ikke klarer å gjenkjenne.

Tenk På Eksemplet Kahneman gir:

Deprimerte barn behandlet med en energidrikk forbedrer seg betydelig over en tre måneders periode. Jeg gjorde opp denne avisoverskriften, men det faktum det rapporterer er sant: hvis du behandlet en gruppe deprimerte barn i noen tid med en energidrikk, ville de vise en klinisk signifikant forbedring. Det er også tilfelle at deprimerte barn som tilbringer litt tid på hodet eller klemmer en katt i tjue minutter om dagen, vil også vise forbedring.

når du kommer over slike overskrifter, er det veldig fristende å hoppe til konklusjonen at energidrikker, står på hodet eller klemmer katter er alle perfekt levedyktige kurer for depresjon. Disse tilfellene representerer imidlertid igjen regresjonen til gjennomsnittet:

Deprimerte barn er en ekstrem gruppe, de er mer deprimerte enn de fleste andre barn-og ekstreme grupper går tilbake til gjennomsnittet over tid. Korrelasjonen mellom depresjonspoengene ved påfølgende anledninger av testing er mindre enn perfekt, så det vil være regresjon til gjennomsnittet: deprimerte barn vil bli noe bedre over tid, selv om de klemmer ingen katter og drikker Ingen Red Bull.

vi ofte feilaktig tilskriver en bestemt politikk eller behandling som årsak til en effekt, når endringen i de ekstreme gruppene ville ha skjedd uansett. Dette gir et grunnleggende problem: hvordan kan vi vite om effektene er reelle eller bare på grunn av variabilitet?Heldigvis er Det En måte å fortelle mellom en reell forbedring og regresjon til gjennomsnittet. Det er innføringen av den såkalte kontrollgruppen, som forventes å bli bedre ved regresjon alene. Målet med forskningen er å avgjøre om den behandlede gruppen forbedrer seg mer enn regresjon kan forklare.

I virkelige situasjoner med ytelsen til bestemte personer eller lag, hvor den eneste virkelige referansen er tidligere ytelse og ingen kontrollgruppe kan innføres, kan effektene av regresjon være vanskelig om ikke umulig å disentangle. Vi kan sammenligne med bransjegjennomsnitt, jevnaldrende i kohortgruppen eller historiske forbedringsnivåer, men ingen av disse er perfekte tiltak.

***

Heldigvis er bevissthet om regresjonen til det gjennomsnittlige fenomenet i seg selv allerede et godt første skritt mot en mer forsiktig tilnærming til å forstå flaks og ytelse.

hvis det er noe å lære fra regresjonen til gjennomsnittet, er det betydningen av sporrekorder i stedet for å stole på engangs suksesshistorier. Jeg håper at neste gang du kommer over en ekstrem kvalitet, delvis styrt av en tilfeldighet, vil du innse at effektene sannsynligvis vil regressere over tid og vil justere dine forventninger tilsvarende.

Hva Du Skal Lese Neste

• Oppgrader din tenkning med 113 mentale modeller forklart.
• Les Om Andre Nivå Tenkning slik at du kan unngå negative konsekvenser.