Redaktørens Notat

følgende student forskning rapporten ble utarbeidet For Professor Judit Kardos’ Math 255 klasse, holdt Ved College Of New Jersey. Dette var et 3-kreditt introduksjonskurs I Matematikkens Historie. Denne rapporten ble regnet opp mot 30% av sluttkarakteren. Det er et eksempel på hva slags historisk forskning studenter kan gjøre ved hjelp av sekundære kilder.

Leonard Eulers Løsning På K Hryvnigsberg-Broproblemet

K Hryvnigsberg

vår historie begynner i det 18. århundre, i Den sjarmerende byen K Hryvnigsberg, Preussen ved Bredden av Pregel-Elven. I 1254 grunnla Tyske riddere byen Königsberg under Ledelse av Bohemian King Ottoker II etter deres andre korstog mot Prøysserne. I Middelalderen ble K@nigsberg en svært viktig by og handelssentrum med sin beliggenhet strategisk plassert på elva. Kunstverk fra det attende århundre viser Kö Som en blomstrende by, hvor flåter av skip fylle Pregel, og deres handel tilbyr en komfortabel livsstil til både lokale kjøpmenn og deres familier. Den sunne økonomien tillot folket i byen å bygge syv broer over elven, hvorav de fleste er koblet Til øya Kneiphof; deres steder kan ses i det medfølgende bildet .

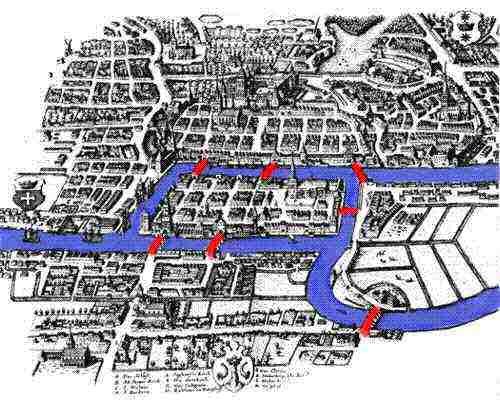
da elven rant rundt Kneiphof, bokstavelig talt betyr pubgård, og en annen øy, delte den byen inn i fire forskjellige regioner. De syv broene ble kalt Blacksmith ‘s bridge, Connecting Bridge, Green Bridge, Merchant’ S Bridge, Wooden Bridge, High Bridge og Honey Bridge. Ifølge lore, innbyggerne I K Hryvnigsberg pleide å tilbringe søndag ettermiddag vandre rundt sin vakre by. Mens du går, folk i byen bestemte seg for å lage et spill for seg selv, deres mål er å tenke ut en måte der de kunne gå rundt i byen, krysset hver av de syv broer bare en gang. Selv om Ingen Av innbyggerne I K Hryvnigsberg kunne finne en rute som ville tillate dem å krysse hver av broene bare en gang, kunne de fortsatt ikke bevise at det var umulig. Heldig For Dem, Königsberg var ikke så langt Fra St. Petersburg, hjemmet til den berømte matematikeren Leonard Euler.

Euler Og Broproblemet

Hvorfor skulle Euler bekymre seg for et problem som ikke er relatert til matematikkfeltet? Hvorfor skulle en så stor matematiker tilbringe mye tid med et trivielt problem som Kö Broproblemet? Euler var åpenbart en travel mann, og publiserte mer enn 500 bøker og papirer i løpet av sin levetid. I 1775 alene skrev han i gjennomsnitt en matematisk papir per uke, og i løpet av sin levetid skrev han på en rekke emner i tillegg til matematikk, inkludert mekanikk, optikk, astronomi, navigasjon og hydrodynamikk. Det er ikke overraskende At Euler følte at dette problemet var trivielt, og skrev i et brev Fra 1736 til Carl Leonhard Gottlieb Ehler, borgermester I Danzig, som ba Ham om en løsning på problemet:

. . . Dermed ser du, mest edle Herre, hvordan denne typen løsning har lite forhold til matematikk, og jeg forstår ikke hvorfor du forventer at en matematiker skal produsere den, heller enn noen andre, for løsningen er basert på grunn alene, og dens oppdagelse er ikke avhengig av noe matematisk prinsipp. På grunn av dette vet jeg ikke hvorfor selv spørsmål som har så lite forhold til matematikk, løses raskere av matematikere enn av andre.

Selv Om Euler fant problemet trivielt, var Han fortsatt fascinert av det. I et brev skrevet samme år Til Giovanni Marinoni, en italiensk matematiker og ingeniør, euler sa,

Dette spørsmålet er så banalt, men syntes for meg verdig oppmerksomhet i at geometri, algebra, eller selv kunsten å telle var tilstrekkelig til å løse det.

Euler trodde dette problemet var relatert til et emne Som Gottfried Wilhelm Leibniz en gang hadde diskutert og lengtet etter å jobbe med, Noe Leibniz referert til som geometria situs, eller geometri av posisjon. Denne såkalte posisjonsgeometrien er det Som nå kalles grafteori, Som Euler introduserer og benytter mens han løser dette berømte problemet.

Eulers Bevis

den 26. August 1735 presenterer Euler et papir som inneholder løsningen På Konigsberg – broproblemet. Han løser både dette spesifikke problemet, samt en generell løsning med et hvilket som helst antall landmasser og et hvilket som helst antall broer. Denne artikkelen, Kalt ‘Solutio problematis ad geometriam situs pertinentis,’ ble senere publisert i 1741 . Eulers papir er delt inn i tjueen nummererte avsnitt, og i det følgende vil En forenklet versjon av eulers avsnitt bli presentert.

i De to første avsnittene i eulers bevis introduserer Han Konigsberg-Broproblemet. I Punkt 1 sier Euler at Han mener at dette problemet gjelder geometri, men ikke geometrien som er kjent av hans samtidige, som involverer målinger og beregninger, men i stedet en ny Type Geometri, Som Leibniz refererte til Som Geometri Av Posisjon. Så i Punkt 2 forklarer Euler for publikum hvordan Konigsberg-problemet fungerer. Euler ga en skisse av problemet (Se Eulers Figur 1), og kalte de syv forskjellige broene: a, b, c, d, e, f og g. I dette avsnittet sier han det generelle spørsmålet om problemet, «Kan man finne ut om det er mulig å krysse hver bro nøyaktig en gang?»

Eulers Figur 1 fra ‘Solutio problematis ad geometriam situs pertinentis,’ Eneströ 53

Etter å ha stilt det generelle spørsmålet Han prøver å løse, begynner Euler å utforske ulike metoder for å finne en løsning. I Punkt 3 forteller euler leseren at For å løse dette spesifikke problemet kunne Han skrive ned alle mulige veier, men denne teknikken ville ta mye tid og ville ikke fungere for større konfigurasjoner med flere broer og landmasser. På grunn av disse problemene bestemte Euler seg for å velge en annen metode for å løse dette problemet. i Punkt 4 begynner han å forenkle problemet ved å finne opp et passende system for å representere krysset av en bro. Euler bestemmer at i stedet for å bruke små bokstaver for å representere krysset av en bro han ville skrive store bokstaver som representerer landmassene. FOR eksempel, refererer Hans Figur 1, AB ville bety en reise som startet i landmasse A, og endte I B. Dessuten, Hvis etter reiser Fra landmasse A Til B, noen bestemmer seg for å flytte Til landmasse D, dette ville bare bli betegnet, ABD. I Punkt 5, Euler fortsetter sin diskusjon om denne prosessen forklarer AT I ABDC, selv om det er fire store bokstaver, bare tre broer ble krysset. Euler forklarer at uansett hvor mange broer det er, vil det være ett brev som representerer den nødvendige krysset. På grunn Av Dette krevde Hele Problemet Med K ③nigsberg Bro syv broer som skulle krysses, og derfor åtte store bokstaver.

I Punkt 6 fortsetter Euler å forklare detaljene i hans metode. Han forteller leseren at hvis det er mer enn en bro som kan krysses når man går fra en landmasse til den andre, spiller det ingen rolle hvilken bro som brukes. For eksempel, selv om det er to broer, a og b, som kan ta en reisende Fra A Til B, spiller Det ingen rolle Med Eulers notasjon hvilken bro som er tatt. I dette avsnittet diskuterer Euler også det spesifikke problemet han har å gjøre med. Han forklarer, ved hjelp av sin opprinnelige figur, At k Hryvnigsberg-problemet trenger nøyaktig åtte bokstaver, hvor parene (A, B) og (A,C) må vises ved siden av hverandre nøyaktig to ganger, uansett hvilket brev som vises først. I tillegg må parene (A, D), (B, D) og (C,D) skje sammen nøyaktig en gang for en bane som krysser hver bro en gang og bare en gang for å eksistere.

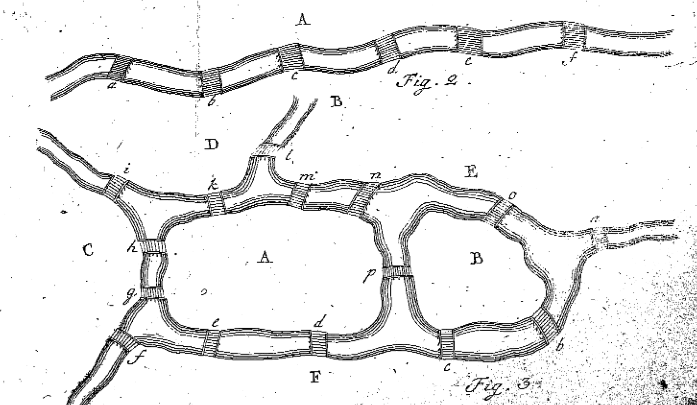
Eulers Tall 2 og 3 fra ‘Solutio problematis ad geometriam situs pertinentis,’ Eneströ 53

I Avsnitt 7 informerer Euler leseren om at han enten må finne en åttebokstavers sekvens som tilfredsstiller problemet, eller at han må bevise at ingen slik sekvens eksisterer. Før Han gjør Dette For Kö Broproblemet, bestemmer han seg for å finne en regel for å finne ut om det finnes en bane for et mer generelt problem. Han gjør dette i Punkt 8 ved å se på mye enklere eksempel på landmasser og broer. Euler tegner Figur 2, og han begynner a vurdere situasjoner Der region A er reist gjennom. Euler sier at hvis bro a er reist en gang, var A enten hvor reisen begynte eller avsluttet, og ble derfor bare brukt en gang. Hvis broer a, b og c er alle reist en gang, brukes a nøyaktig to ganger, uansett om det er start-eller sluttstedet. På samme måte, hvis fem broer fører Til A, vil landmassen A oppstå nøyaktig tre ganger i reisen. Euler sier at » generelt, hvis antall broer er et oddetall, og hvis det økes med en, så er antall forekomster av a halvparten av resultatet.»Med andre ord, hvis Det er et merkelig antall broer som forbinder A med andre landmasser, legg til en til antall broer, og del det med to, for å finne ut hvor mange ganger A må brukes i banen, hvor hver bro brukes en gang og bare en gang (dvs. Totale Forekomster av A hvor A har en merkelig # av broer = (#Av Broer-1) / 2).

Ved å Bruke dette faktum løser Euler Problemet Med Kö Bro i Punkt 9. I sa fall, siden det er fem broer som forer Til A, ma det skje tre ganger (se Hans Figur 1, ovenfor). På Samme måte må B, C og D vises to ganger siden de alle har tre broer som fører til dem. Derfor 3(For A) + 2(For B) + 2(For C) + 2(For D) = 9, Men Euler sa allerede at det bare må være åtte forekomster for de syv broene. Dette er en motsetning! Derfor er det umulig å reise broene i Byen K Hryvnigsberg en gang og bare en gang. Slutten, eller er det? Mens Folk I Königsberg kan være fornøyd med denne løsningen, var den store matematikeren Leonhard Euler ikke fornøyd. Euler fortsetter videre sitt bevis for å håndtere mer generelle situasjoner.

Eulers Generalisering

I Avsnitt 10 fortsetter Euler sin diskusjon ved å merke seg at hvis situasjonen involverer alle landmasser med et ulikt antall broer, er det mulig å fortelle om en reise kan gjøres ved å bruke hver bro bare en gang. Euler sier at hvis summen av antall ganger hver bokstav må vises er en mer så det totale antall broer, en reise kan gjøres. Men hvis antall forekomster er større enn en mer enn antall broer, kan det ikke gjøres en reise, som K@nigsberg Broproblem. Dette skyldes at regelen, Som Euler gir for et oddetall antall broer, ved Hjelp av Figur 2, gjelder for den generelle situasjonen om det bare er en annen landmasse eller mer enn en.

I Avsnitt 11 og 12 omhandler Euler situasjonen der en region har et jevnt antall broer knyttet til den. Denne situasjonen vises ikke I Kö-Problemet, og har derfor blitt ignorert til nå. I situasjonen Med en landmasse X Med et jevnt antall broer kan to tilfeller forekomme. Det første tilfellet er Når X er utgangspunktet for reisen. I Dette tilfellet vil X vises to ganger, en gang som utgangspunkt, og igjen som sluttpunkt. I det andre tilfellet Er X ikke utgangspunktet. Hvis Dette skulle skje, Ville X bare vises en gang, da reisen måtte gå inn gjennom en bro og umiddelbart gå gjennom den eneste andre tilgjengelige. På samme måte, hvis det er fire broer festet Til X, avhenger antall forekomster Av X av om det er et utgangspunkt eller ikke. Hvis reisen starter i X, må den vises tre ganger, men hvis den ikke begynner I X, vil den bare vises to ganger. Så generelt, Hvis X har et jevnt antall broer festet, så hvis reisen ikke starter I X, Vises x halvparten av antall ganger som broer (dvs. Forekomster Av X hvor X er jevn og ikke utgangspunktet = (#Av Broer) / 2). Hvis reisen starter I X, vises x halvparten av antall ganger som broer, pluss en (Dvs. Forekomster Av X hvor X er jevn og utgangspunkt = ((# Av Broer) / 2) + 1).

I Avsnittene 13 til 15 forklarer Euler hvordan man finner ut om en bane som bruker hver bro en gang og bare en gang eksisterer, og presenterer sitt eget eksempel for å vise hvordan den fungerer. Euler forklarer først sin enkle seks-trinns metode for å løse enhver generell situasjon med landmasser delt av elver og forbundet med broer. Første euler betegner hver landmasse med et stort brev. For det andre tar han totalt antall broer, legger til en, og skriver dette over diagrammet han skal lage. Deretter tar han store bokstaver, legger dem i en kolonne, og ved siden av dem skriver antall broer. For det fjerde indikerer han med stjerner landmassene som har et jevnt antall broer. Deretter, ved siden av hvert partall, skriver han ½ av antall og ved siden av hvert oddetall han plasserer ½ antall pluss en. Til Slutt legger Euler til tallene som er skrevet i kolonnen til høyre, og hvis summen er en mindre enn eller lik antall broer pluss en, så er den nødvendige reisen mulig. Det er imidlertid viktig å merke seg at hvis summen er en mindre enn antall broer pluss en, må reisen starte fra en av landmassene merket med en stjerne. Hvis summen er lik antall broer pluss en, må reisen starte i en region som ikke er merket med en stjerne.

Eksempler

Ved Å Bruke Konigsberg-problemet som sitt første eksempel, viser Euler følgende:

antall broer = 7, antall broer pluss en = 8

Regionen Broer Ganger Regionen Må Vises

A 5 3

B 3 2

C 3 2

d 3 2

, 3 + 2 + 2 + 2 = 9, som er mer enn 8, så reisen er umulig.Siden dette eksemplet er ganske grunnleggende, bestemmer Euler seg for å designe sin egen situasjon med to øyer, fire elver og femten broer. Situasjonen Euler opprettet kan ses i Sin Figur 3, ovenfor. Euler forsøker nå å finne ut om det er en sti som gjør at noen kan gå over hver bro en gang og bare en gang. Euler følger de samme trinnene som ovenfor, navngir de fem forskjellige regionene med store bokstaver, og lager et bord for å sjekke det om det er mulig, som følgende:

Antall broer = 15, antall broer pluss en = 16

A* 8 4

B* 4 2

D 3 2

e 5 3

f* 6 3

i tillegg, 4 + 2 + 2 + 2 + 3 + 3 = 16, som tilsvarer antall broer, pluss en, noe som betyr at reisen faktisk er mulig. Siden summen er lik antall broer pluss en, må reisen starte I Enten D Eller E. Nå Som Euler vet at det er mulig å gjøre en reise, er alt han trenger å gjøre, å angi hva veien vil være. Euler velger stien EaFbBcFdAeFfCgAhCiDkAmEnApBoElD, hvor han inkluderer hvilke broer som krysses mellom bokstavene som representerer landmassene. Selv om denne informasjonen er overflødig, da den nøyaktige broen ikke spiller noen rolle i å vite at en reise er mulig, er det nyttig når du velger en sti. Dette er et godt eksempel som viser metoden Som Euler ville bruke når du løser et problem av denne art.

Eulers Konklusjoner

I de neste par avsnittene presenterer Euler en annen måte å finne ut om en reise kan gjøres gitt et sett landmasser, broer og elver. I Punkt 16 påpeker Euler at summen av tallene som er oppført direkte til høyre for landmassene, legger opp til dobbelt så mange broer. Dette faktum blir senere kjent som handshaking lemma. I utgangspunktet sier handshaking lemma at hver bro teller to ganger, en gang for hver landmasse som den er festet til. I Punkt 17 fortsetter Euler å si at summen av alle broene som fører til hver region er jevn, siden halvparten av dette tallet er lik det totale antall broer. Dette er imidlertid umulig hvis det er et merkelig antall landmasser med et merkelig antall broer. Derfor viser Euler at Hvis det er noen odde tall knyttet til landmasser, må det være et jevnt antall av disse landmassene.

dette er Imidlertid Ikke nok til å bevise når det er en sti hvor hver bro brukes en gang og bare en gang, Da Kö Broproblemet har et jevnt antall landmasser med et merkelig antall broer som går til dem. På grunn av Dette legger Euler til flere begrensninger I Punktene 18 og 19. Euler forklarer at siden summen av antall broer knyttet til hver landmasse er lik to ganger antall broer( som sett i handshaking lemma), så derfor hvis du legger to til denne summen og deretter deler med to, vil du få antall totale broer pluss en. Dette nummeret er det samme som det som ble brukt før, som brukes til å fortelle om en bane er mulig. Hvis alle tallene er like, vil den tredje kolonnen i tabellen summere til en mindre enn totalt antall broer pluss en.

euler forklarer da at det er åpenbart at hvis det er to landmasser med et merkelig antall broer, vil reisen alltid være mulig hvis reisen starter i en av regionene med et merkelig antall broer. Dette skyldes at hvis de jevne tallene halveres, og hver av de odde er økt med en og halvert, vil summen av disse halvdelene være lik en mer enn det totale antall broer. Men hvis det er fire eller flere landmasser med et merkelig antall broer, er det umulig for det å være en sti. Dette er fordi summen av halvdelene av oddetall pluss en sammen med summen av alle halvdelene av partall vil gjøre summen av den tredje kolonnen større enn det totale antall broer pluss en. Derfor viste Euler bare at det maksimalt kan være to landmasser med et merkelig antall broer.

Når Dette er sagt, Kan Euler nå trekke sine konklusjoner om mer generelle former For Kö Broproblemet. I Punkt 20 gir Euler de tre retningslinjene som noen kan bruke til å finne ut om en bane eksisterer ved å bruke hver bro en gang og bare en gang. For det første hevdet han om det er mer enn to landmasser med et merkelig antall broer, så er det ikke mulig med en slik reise. For det andre, hvis antall broer er merkelig for nøyaktig to landmasser, så er reisen mulig hvis den starter i en av de to odde nummererte landmassene. Til Slutt sier Euler at Hvis det ikke er noen regioner med et merkelig antall landmasser, kan reisen oppnås i en hvilken som helst region. Etter å ha oppgitt disse tre fakta, avslutter Euler sitt bevis Med Avsnitt 21, som ganske enkelt sier at etter at man har funnet ut at en sti eksisterer, må De fortsatt gå gjennom innsatsen for å skrive ut en sti som fungerer. Euler mente metoden for å oppnå dette var trivielt, og han ønsket ikke å bruke mye tid på det. Imidlertid foreslo Euler å konsentrere seg om hvordan man kommer fra en landmasse til den andre, i stedet for å konsentrere seg om de spesifikke broene først.

Eulers Bevis og Grafteori

når man leser eulers opprinnelige bevis, oppdager man et relativt enkelt og lett forståelig arbeid i matematikk; det er imidlertid ikke det faktiske beviset, men mellomtrinnene som gjør dette problemet kjent. Eulers store nyskapning var å se På broproblemet k ④nigsberg abstrakt, ved å bruke linjer og bokstaver for å representere den større situasjonen for landmasser og broer. Han brukte store bokstaver for å representere landmasser, og små bokstaver for å representere broer. Dette var en helt ny type tenkning for tiden, Og I hans papir utløste Euler ved et uhell en ny gren av matematikk kalt grafteori, hvor en graf bare er en samling av hjørner og kanter. I dag kalles en bane i en graf, som inneholder hver kant av grafen en gang og bare en gang, En eulerisk sti på grunn av dette problemet. Fra Den tiden euler løste dette problemet til i dag, har grafteori blitt en viktig gren av matematikk, som styrer grunnlaget for vår tenkning om nettverk.

Königsberg broproblemet er hvorfor Biggs sier,

opprinnelsen til grafteori er ydmyk, selv frivoløs … problemene som førte til utviklingen av grafteori var ofte lite mer enn gåter, designet for å teste oppfinnsomheten i stedet for å stimulere fantasien. Men til tross for den tilsynelatende trivialiteten til slike gåter, fanget de matematikernes interesse, med det resultat at grafteori har blitt et emne rik på teoretiske resultater av overraskende variasjon og dybde.

Som Biggs ‘ uttalelse skulle tilsi, er dette problemet så viktig at det er nevnt i første kapittel av Hver Grafteori bok som ble gjennomgått i biblioteket.etter eulers oppdagelse (eller oppfinnelse, avhengig av hvordan leseren ser på det), økte grafteorien med store bidrag fra store matematikere som Augustin Cauchy, William Hamilton, Arthur Cayley, Gustav Kirchhoff og George Polya. Disse mennene bidro alle til å avdekke «omtrent alt som er kjent om store, men bestilte grafer, for eksempel gitteret dannet av atomer i en krystall eller det sekskantede gitteret laget av bier i et bikube .»Andre kjente grafteori problemer inkluderer å finne en måte å flykte fra en labyrint eller labyrint, eller finne rekkefølgen på trekk med en ridder på et sjakkbrett slik at hver rute er landet på bare en gang og ridderen vender tilbake til rommet der han begynte . Noen andre grafteoriproblemer har gått uløste i århundrer .

Skjebnen Til K Hryvnigsberg

mens grafteorien oppsving etter At Euler løste Problemet Med K Hryvnigsberg-Broen, hadde Byen K Hryvnigsberg en helt annen skjebne. I 1875 bestemte folket I K Hryvnigsberg seg for å bygge en ny bro, mellom noder B og C, og økte antall koblinger til Disse to landmassene til fire. Dette betydde at bare to landmasser hadde et merkelig antall lenker, noe som ga en ganske enkel løsning på problemet. Opprettelsen av den ekstra broen kan eller ikke har vært ubevisst forårsaket av ønsket om en bane for å løse byens berømte problem. en ny bro løste imidlertid ikke Alle K Hryvnigsbergs fremtidige problemer, da byen ikke forventet tilbake i det nittende århundre, «den triste og krigsherjede skjebnen som ventet det som vert for en Av DE voldsomste slagene I ANDRE VERDENSKRIG.»I løpet av fire dager i August 1944 ødela Britiske bombefly både den gamle bydelen og de nordlige delene Av K Hryvnigsberg. I januar og februar 1945 er Regionen Rundt K Hryvnigsberg omgitt av russiske styrker. Tyske sivile begynner å evakuere fra byen, men beveger seg for sent. Tusenvis av mennesker blir drept prøver å flykte med båt og til fots over det iskalde vannet I Curonian Lagoon. I April 1945, den Røde Hær fanger K Hryvnigsberg Med om lag nitti prosent av gamlebyen ligger i ruiner.

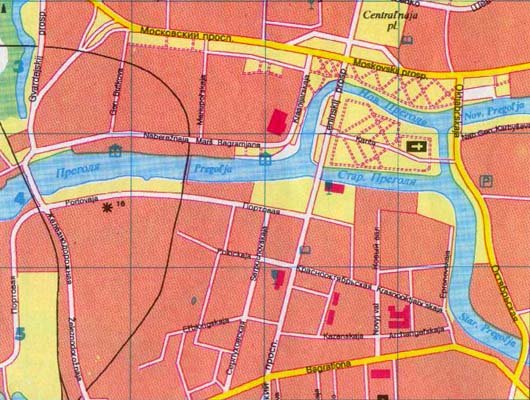
Nedenfor finner du et kart Over Kö Dette kartet viser hvor mye byen har endret seg. Mange av broene ble ødelagt under bombene, og byen kan ikke lenger stille det samme spennende spørsmålet de kunne i det attende århundre. Sammen med en helt annen layout, byen K Hryvnigsberg har et nytt navn, Kaliningrad, med elven Pregel omdøpt Pregolya . Mens skjebnen Til K Hryvnigsberg er forferdelig, borgernes gamle kaffehus problem med å krysse hver av sine gamle syv broer nøyaktig en gang førte til dannelsen av en helt ny gren av matematikk, grafteori.

Biggs, Norman L., E. K. Lloyd og Robin J. Wilson. Grafteori: 1736-1936. Oxford: Clarendon Press, 1976.Dunham, William. Euler: Mesteren Av Oss Alle. Washington: Matematisk Forening Av Amerika, 1999.

Euler, Leonhard, ‘Løsning på problemer med geometrisk tilpasning’ (1741), Eneströ 53, MAA Euler Arkiv.

«Matematikkens Historie: På Leonhard Euler (1707-1783).»ScienceWeek (2003). 6 November. 2005.

Hopkins, Brian Og Robin Wilson. «Sannheten Om Königsberg.»College Matematikk Journal (2004), 35, 198-207.

«Konigsberg Broer.»MacTutor Matematikkens Historie Arkiv:
http://www-history.mcs.st – and.ac.uk/history/Miscellaneous/other_links/Konigsberg.html

Redaktørens notat: Denne artikkelen ble opprinnelig publisert I Convergence, Volume 3 (2006).