2.5: Darcys Lovflyt i Et Porøst Medium
Darcys lov er avgjørende for å forstå mange grener av geologi, spesielt hydrogeologi. Før vi ser på loven og hva den kan fortelle oss, la oss se på hvordan den ble utviklet. Darcys lov er oppkalt Etter Henry Darcy, en fransk ingeniør fra det 19. århundre som utviklet et underjordisk trykkrør for å levere vann rundt Byen Dijon. Systemet, som også ga vann til de berømte Dijon-fontenene, revolusjonerte byens vann-og kloakksystemer. Systemet krevde ingen pumper og ble drevet rent av tyngdekraften. Under prosessen med å utvikle det nye systemet gjennomførte Darcy en rekke eksperimenter der Han prøvde å flytte vann utelukkende ved hjelp av tyngdekraften.
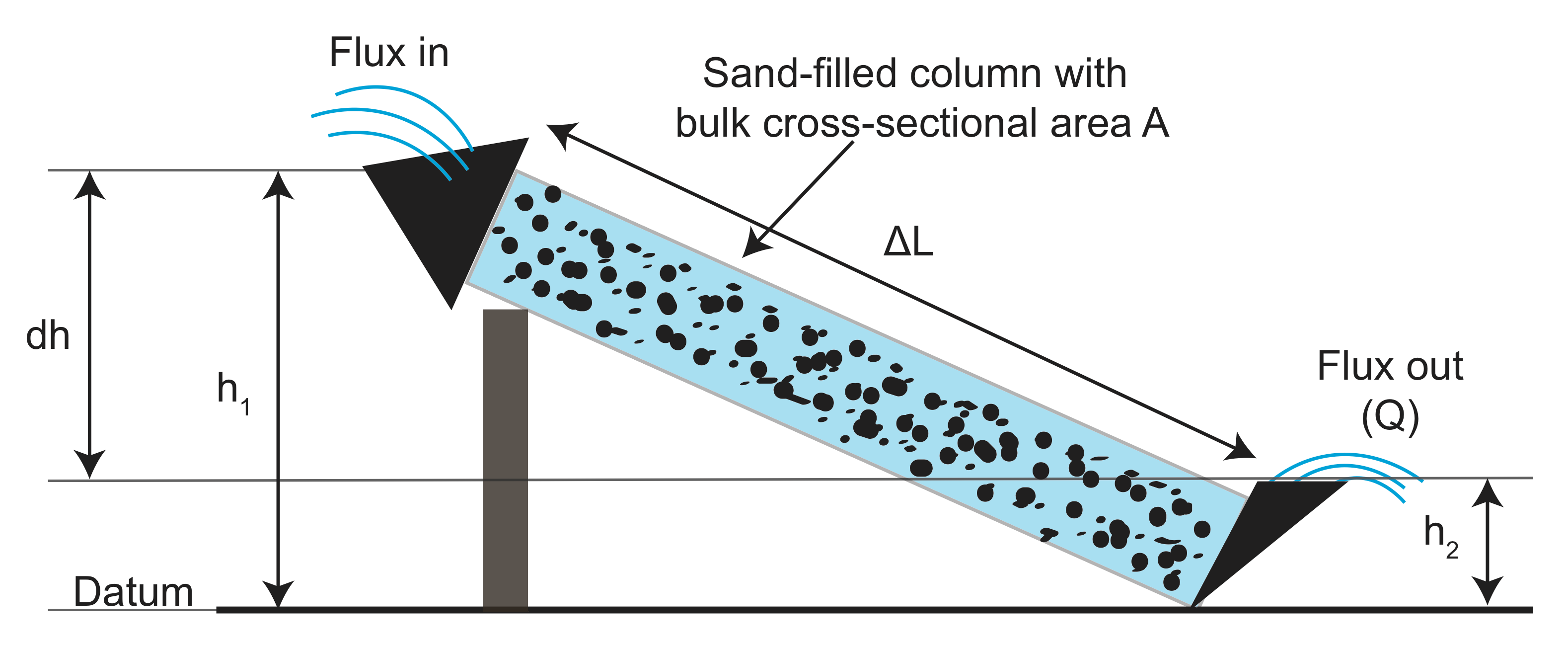
fra forsøkene samlet data om lengden på flume (\(L\)), tverrsnittsarealet av flume (\(A\)), høydeforskjellen (\(h_1 – h_2\)) og fluxen av vann som kommer ut \(Q\) både med og uten granulært (filtrering) materiale i flume. Han plottet deretter fluxmålingen normalisert av området versus forholdet mellom høydeforskjellen og lengden på flumen (\(\frac{h_1-h_2}{l}\)). Det han fant er at det er et lineært forhold, og hellingen avhenger av det granulære materialet han brukte i flume:
\
som kan omskrives som et derivat,
\
hvor \(K\) er den hydrauliske ledningsevnen og \(\frac{dh}{dx}\) er den hydrauliske gradienten. \(Q\), den totale utslippshastigheten, har enheter av \(\frac{m^3}{s}\), volumet av vann per gang. Det negative tegnet skyldes at væsken strømmer ned (negativ) den hydrauliske gradienten fra høyere verdier til lavere verdier.
hydraulisk ledningsevne er en fysisk parameter som står for hvor lett væsken kan bevege seg gjennom poreområdet for materialet. I Darcys opprinnelige eksperimenter brukte Han sand med forskjellige kornstørrelser, men den hydrauliske ledningsevnen kan også bestemmes for faste bergarter, da de fleste bergarter har litt poreplass.Etter Darcys opprinnelige eksperimenter ble Det gjort ytterligere arbeid for å forstå de fysiske egenskapene til væsken og steinen som bestemmer den effektive hydrauliske ledningsevnen. Fra disse forsøkene ble det funnet at
\
hvor \(k\) er den indre permeabiliteten til det porøse mediet (det faste stoffet), \(\eta\) er væskens dynamiske viskositet, og \(\gamma = \rho g\) er væskens spesifikke vekt, som avhenger av væsketettheten, \(\rho\) og tyngdekraften, \(g\).
den uthevede kolonnen I figuren Er K, den hydrauliske ledningsevnen i \(\frac{m}{s}\); dette er enhetene vi skal bruke. Den hydrauliske ledningsevne er også noen ganger rapportert i form av den iboende permeabilitet, \(k\), med enheter av darcys eller cm2. Hele spekteret av verdier for hydraulisk ledningsevne er 1-10-13 \(\frac{m}{s}\). Eksperimenter Som Darcys brukes til å måle K i ekte materialer.
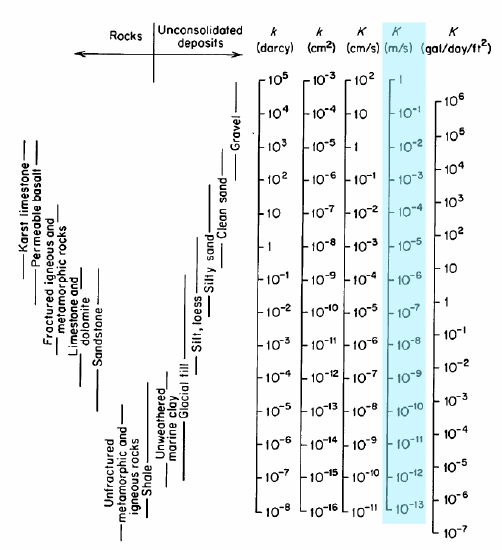
utslippshastigheten \(Q\) er en volumfluss (\(m^3/S\)), Men Vi Tenker Vanligvis På Væskestrøm I Form Av Hastighet Eller Hastighet. Utladningsspørsmålene kan omarrangeres ved å dele gjennom området for å definere Darcy Flux
\\]
Eller i form av den indre permeabiliteten og trykkgradienten,
\
hvor \(\eta\) er væskeviskositeten (se nedenfor for avledning av den andre ligningen).Det er viktig å merke Seg At Darcy flux ikke er lik fluidhastigheten, selv om Den er i hastighetsenheter. Fluidhastigheten er funnet gjennom den gjennomsnittlige lineære hastigheten (\(v_a\)), som er gjennomsnittlig av hastigheten til alle mulige fluidbaner gjennom det porøse mediet: men å finne denne verdien er utenfor omfanget av denne klassen. I stedet vil vi merke at fluidhastigheten er
\
hvor \(\varphi\) er porøsiteten og v er fluidhastigheten. Porøsiteten, \(\varphi\) beregnes som forholdet mellom volumet av tomrom til det totale volumet av et materiale \(\varphi=\frac{V_{void}}{V_{tot}}\), og uttrykkes vanligvis som en brøkdel mellom 0 og 1 eller som en prosent. Merk at hvis \(\varphi \ leq\) 1 så er fluidhastigheten større darcy flux.Et annet begrep som oppstår når man diskuterer flyt gjennom bergarter og ukonsoliderte materialer er permeabilitet. Mens porøsitet er den faktiske brøkdel av porer (hulrom) i fjellet, kan disse hulrommene ha forskjellige former og forskjellig tilkobling, noe som påvirker hvor lett en væske kan bevege seg gjennom poreområdet. Permeabiliteten er et mål på hvor enkelt væsker og gasser kan passere gjennom en stein. Jo mer konsolidert materialet, desto lavere er dets permeabilitet. Dermed har» løse » materialer som grus høy permeabilitet. Noen bergarter kan også ha anisotrop permeabilitet, noe som betyr at væsker kan strømme lett i en retning, men ikke i en annen. Et eksempel på en stein med anisotrop permeabilitet er en skifer. Væsker kan bevege seg lett i et lag av skifer, men kan ikke bevege seg over lag.
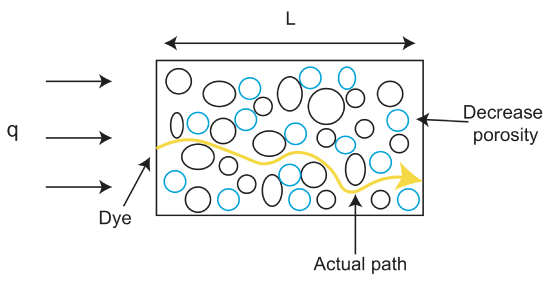
Væskehastighet
La oss gjøre et grunnleggende eksempel.
Vi får det \(q=2\frac{m}{min}\) og \(\varphi\) er 25% og vil finne fluidhastigheten.
vi konverterer først 25% til 0,25.
Deretter, \(v=\frac{2}{0.25}\frac{m}{min}\)
og
\(v = 8 \frac{m} {min}\) er fluidhastigheten.
Hydraulisk Hode
Tilbake Til Darcys eksperimenter, hva er fysisk prosess som faktisk driver væskestrømmen gjennom flumen?begrepet \(\frac{dh}{dx} \) refereres til som det hydrauliske hodet, som er væsketrykket på grunn av vekten av en væske i forhold til noen referanseplassering: en trykkgradient. Men \(\frac{dh}{dx}\) har ikke enheter av trykk per lengde, så hvorfor kalles det hydrauliske hodet?
la oss vurdere hva trykket er i røret i Darcys eksperimenter. For å gjøre forsøkene hadde Darcy en tank med vann i den øvre enden av røret som gir et konstant vannnivå på toppen av røret, tilsvarende høyden på røret, \(h_1\). På samme måte var det en tank på bunnen med et konstant vannnivå som tilsvarer \(h_2\). Derfor er væsketrykket i hver av tankene på grunn av vekten av vannet gitt av \(P = \ rho g h\). Trykkgradienten mellom toppen og bunnen av plommen Er da
\
eller
\
\ & =\frac{K}{\rho g}\frac{dp}{dx} \ end{align}. \ ]
Recall, ovenfra at den hydrauliske ledningsevne kan skrives i form av den iboende permeabilitet som \(K = k \ frac {\gamma} {\eta}\) som er ekvivalent med \(k \ frac {\rho g} {\eta} \) eller omorganisere, \(\frac{K}{\rho g} = \frac{k}{\eta} \). Derfor kan Vi erstatte Å gi To ekvivalente uttrykk For Darcys Lov, med en interms av gradienten i høyde,
\
og den andre i form av gradienten i trykk,
\
\
således kalles \(\frac{dh}{dx}\) det hydrauliske hodet fordi den fysiske opprinnelsen til begrepet I Darcys Lov er trykkgradienten i væsken, som driver strømmen.
Vann forlater En Akvifer
La oss nå gjøre et eksempel som beregner væskehastigheten til vann som kommer inn i en akvifer. I skissen under akviferhøyden følger topografien på bakken ved siden av dalen med strømmen. Vann strømmer fra høyt trykk (hodehøyde) mot dalen og forlater akvariet ved strømmen. Vi kan bruke Darcys Lov til å estimere vannstrømmen fra akvariet.
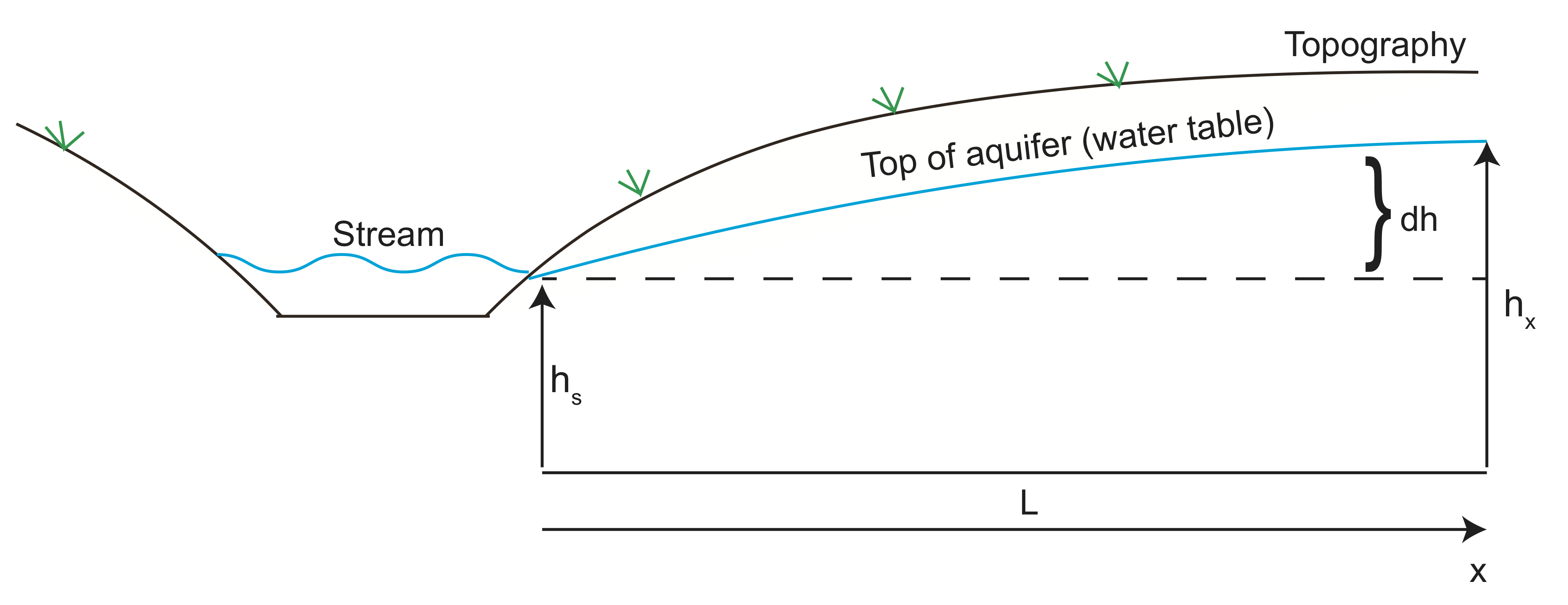
ved hjelp av geofysisk avbildning er høyden på akvariet funnet å være 10 m (\(dh\)) over strømhøyden ca 100 meter (\(L\)) unna. Anta at den hydrauliske ledningsevnen er \ (K=10^{-6}\) m / s og porøsiteten er \(\varphi=30\)%.
fluksen er

Laminær versus Turbulent Strømning
En av de implisitte forutsetningene I Darcys lov er at strømmen er laminær. Laminær strømning er karakterisert som består av tynne lag eller laminae av væske som alle beveger seg parallelt med hverandre. I motsetning turbulent flyt er preget av virvler, virvler og virvler, der tilstøtende lag av væske divergerer og ta forskjellige veier ned strømmen.
En måte vi kan kvantifisere om en væske er laminær eller turbulent, er ved å beregne Reynolds tall for strømmen, definert som
\
Reynolds tall er funnet ved å vurdere de to begrepene i momentumbalansen for strømmen. Den første termen er treghetskraften per volumenhet, som driver strømmen, \(\rho u \ frac{du}{dx}\). Den andre termen er den viskøse kraften per volum, som motstår strømning, \(\eta\frac{d^2u}{dx^2}\). Disse to begrepene må balansere, slik at vi kan sette dem like,
\
Neste omskriver vi vilkårene, på en forenklet måte for å fange bare de relevante dimensjonene til variablene. For å gjøre det, går vi gjennom det som kalles en dimensjonal analyse, hvor vi erstatter hver variabel med referanseverdier, ganger en ikke-dimensjonal form av variabelen.
for eksempel for termen \(x\) er omskrevet som bare \(L x’\), hvor \(L\) er referanselengden (væskedybden) og \(x’\) er den ikke-dimensjonale avstanden. På samme måte lar vi \(u = u_o u’\). Ved å erstatte disse i ligningen får vi
\
Neste kombinerer vi de konstante verdiene ut foran
\
Merk at kombinasjonen av variabler foran er Reynolds tall
\
hvor variablene er \(u_o\) strømningshastighet, l væskedybde og variablene vi har sett tidligere, \(\rho\) væsketetthet og \(\eta\) væskeviskositet. Ved å gå gjennom denne analysen finner vi at enhver flyt som er preget av balansen mellom disse to begrepene, kan sammenlignes ved å bare vite verdien Av Reynolds’ tall. For eksempel, hvis en strøm har en viskositet som er 10 ganger viskositeten i en annen strøm, vil de to strømmer oppføre seg det samme er tettheten (eller hastigheten eller lengden) økes også med en faktor på 10 for høyere viskositet tilfelle; det Vil Si At Reynolds-tallet for de to strømmer er det samme.
For Å ha Darcy flow må Reynolds tall være mindre enn 1-10 (laminær). For \(Re > 1-10 \) er strømmen ikke strengt laminær, men den er ennå ikke turbulent(ikke-lineær, ikke-laminær). For å ha turbulent strømning må Reynolds tall være større enn rundt 2000.
Forstå at konstantene i telleren og nevnen påvirker strømningens egenskaper på motsatt måte, bidrar også til å tenke på hvordan forskjellige væsker vil oppføre seg under lignende ytre forhold. For eksempel vil en tettere fluid som ogsa har en rask hastighet ha en hoyere Re og utvise turbulent oppforsel. I motsetning til dette vil en væske som is som har høy viskositet og beveger seg veldig sakte, ha lav Re og vil sannsynligvis ha laminær strømning. Isens høye viskositet virker for å stabilisere strømmen. Som et annet eksempel, kan to væsker begge bevege seg med samme hastighet oppføre seg annerledes hvis de andre verdiene i Reynolds tall \(\frac {\rho l} {\mu}\) er forskjellige. Derfor avhenger flytypen ikke bare av strømningshastigheten, men på kombinasjonen av variabler i Reynolds tall.
Anvendelse Av Darcys Flow
Darcys lov er hovedligningen som styrer flyt i akviferer og brønner. Uten Det ville vi ikke kunne bore brønner eller forstå vannbevegelse i akviferer, spesielt i Californias central valley, hvor begge disse ideene er avgjørende for både landbruksproduktivitet og grunnvannssynking.
