Nota del editor

El siguiente informe de investigación del estudiante fue preparado para la clase de Matemáticas 255 de la profesora Judit Kardos, celebrada en el College of New Jersey. Este fue un curso introductorio de 3 créditos en la Historia de las Matemáticas. Este informe se contabilizó para el 30% de la calificación final. Es un ejemplo del tipo de investigación histórica que los estudiantes pueden hacer usando fuentes secundarias.

La solución de Leonard Euler al problema del puente de Königsberg

Königsberg

Nuestra historia comienza en el siglo XVIII, en la pintoresca ciudad de Königsberg, Prusia, a orillas del río Pregel. En 1254, los caballeros teutónicos fundaron la ciudad de Königsberg bajo la dirección del rey bohemio Ottoker II después de su segunda cruzada contra los prusianos. En la Edad Media, Königsberg se convirtió en una ciudad muy importante y centro comercial con su ubicación estratégicamente ubicada en el río. Obras de arte del siglo XVIII muestran a Königsberg como una ciudad próspera, donde flotas de barcos llenan el Pregel, y su comercio ofrece un estilo de vida cómodo tanto a los comerciantes locales como a sus familias. La economía saludable permitió a la gente de la ciudad construir siete puentes a través del río, la mayoría de los cuales conectaban con la isla de Kneiphof; sus ubicaciones se pueden ver en la imagen adjunta .

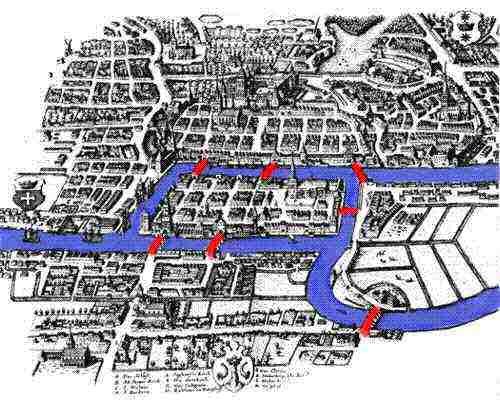
A medida que el río fluía alrededor de Kneiphof, que literalmente significa patio de pub, y otra isla, dividió la ciudad en cuatro regiones distintas. Los siete puentes se llamaban Puente de Herrero, Puente de Conexión, Puente Verde, Puente de Comerciante, Puente de Madera, Puente Alto y Puente de Miel. Según la tradición, los ciudadanos de Königsberg solían pasar las tardes de domingo paseando por su hermosa ciudad. Mientras caminaban, la gente de la ciudad decidió crear un juego para sí mismos, su objetivo era idear una forma en la que pudieran caminar por la ciudad, cruzando cada uno de los siete puentes una sola vez. A pesar de que ninguno de los ciudadanos de Königsberg pudo inventar una ruta que les permitiera cruzar cada uno de los puentes una sola vez, no pudieron probar que era imposible. Por suerte para ellos, Königsberg no estaba muy lejos de San Petersburgo, hogar del famoso matemático Leonard Euler.

Euler y el problema del Puente

¿Por qué Euler se preocuparía por un problema tan ajeno al campo de las matemáticas? ¿Por qué un gran matemático pasaría tanto tiempo con un problema trivial como el Problema del Puente de Königsberg? Euler era obviamente un hombre ocupado, publicando más de 500 libros y documentos durante su vida. Solo en 1775, escribió un promedio de un artículo matemático por semana, y durante su vida escribió sobre una variedad de temas además de las matemáticas, incluida la mecánica, la óptica, la astronomía, la navegación y la hidrodinámica. No es de extrañar que Euler sintiera que este problema era trivial, declarando en una carta de 1736 a Carl Leonhard Gottlieb Ehler, alcalde de Danzig, quien le pidió una solución al problema :

. . . Así ve, muy noble Señor, cómo este tipo de solución tiene poca relación con las matemáticas, y no entiendo por qué espera que lo produzca un matemático, en lugar de cualquier otro, porque la solución se basa solo en la razón, y su descubrimiento no depende de ningún principio matemático. Debido a esto, no sé por qué incluso las preguntas que tienen tan poca relación con las matemáticas se resuelven más rápidamente por los matemáticos que por otros.

A pesar de que Euler encontró el problema trivial, todavía estaba intrigado por él. En una carta escrita el mismo año a Giovanni Marinoni, un matemático e ingeniero italiano, Euler dijo ,

Esta pregunta es tan banal, pero me pareció digna de atención en que la geometría, ni el álgebra, ni siquiera el arte de contar era suficiente para resolverla.

Euler creía que este problema estaba relacionado con un tema que Gottfried Wilhelm Leibniz había discutido una vez y con el que deseaba trabajar, algo a lo que Leibniz se refería como geometria situs, o geometría de posición. Esta llamada geometría de posición es lo que ahora se llama teoría de grafos, que Euler introduce y utiliza para resolver este famoso problema.

La prueba de Euler

El 26 de agosto de 1735, Euler presenta un documento que contiene la solución al problema del puente de Konigsberg. Aborda este problema específico, así como una solución general con cualquier número de masas terrestres y cualquier número de puentes. Este documento, llamado ‘Solutio problematis ad geometriam situs pertinentis’, fue publicado más tarde en 1741 . El documento de Euler se divide en veintiún párrafos numerados, y en lo que sigue, se presentará una versión simplificada de los párrafos de Euler.

En los dos primeros párrafos de la prueba de Euler, introduce el problema del puente de Konigsberg. En el párrafo 1, Euler afirma que cree que este problema se refiere a la geometría, pero no a la geometría bien conocida por sus contemporáneos, que involucra mediciones y cálculos, sino a un nuevo tipo de Geometría, a la que Leibniz se refirió como Geometría de Posición. Luego, en el párrafo 2, Euler explica a su audiencia cómo funciona el problema de Konigsberg. Euler proporcionó un bosquejo del problema (véase la Figura 1 de Euler), y llamó a los siete puentes distintos: a, b, c, d, e, f y g. En este párrafo, expone la pregunta general del problema: «¿Se puede averiguar si es posible cruzar cada puente exactamente una vez?»

Figura 1 de Euler de ‘Solutio problematis ad geometriam situs pertinentis,’ Eneström 53

Después de exponer la pregunta general que está tratando de resolver, Euler comienza a explorar diferentes métodos para encontrar una solución. En el párrafo 3, Euler le dice al lector que para resolver este problema específico, podría escribir todos los caminos posibles, pero esta técnica tomaría mucho tiempo y no funcionaría para configuraciones más grandes con más puentes y masas de tierra. Debido a estos problemas, Euler decidió elegir un método diferente para resolver este problema.

En el párrafo 4, comienza a simplificar el problema inventando un sistema conveniente para representar el cruce de un puente. Euler decide que en lugar de usar las letras minúsculas para representar el cruce de un puente, escribiría las letras mayúsculas que representan las masas de tierra. Por ejemplo, haciendo referencia a su Figura 1, AB significaría un viaje que comenzó en la masa de tierra A y terminó en B. Además, si después de viajar de la masa de tierra A a B, alguien decide mudarse a la masa de tierra D, esto simplemente se denotaría, ABD. En el párrafo 5, Euler continúa su discusión sobre este proceso explicando que en ABDC, aunque hay cuatro letras mayúsculas, solo se cruzaron tres puentes. Euler explica que no importa cuántos puentes haya, habrá una letra más para representar el cruce necesario. Debido a esto, todo el problema del puente de Königsberg requería que se cruzaran siete puentes, y por lo tanto ocho letras mayúsculas.

En el párrafo 6, Euler continúa explicando los detalles de su método. Le dice al lector que si hay más de un puente que se puede cruzar al ir de una masa de tierra a la otra, no importa qué puente se use. Por ejemplo, aunque hay dos puentes, a y b, que pueden llevar a un viajero de A a B, no importa con la notación de Euler qué puente se toma. En este párrafo, Euler también discute el problema específico que está tratando. Él explica, usando su figura original, que el problema de Königsberg necesita exactamente ocho letras, donde los pares de (A, B) y (A, C) deben aparecer uno al lado del otro exactamente dos veces, sin importar qué letra aparezca primero. Además, los pares (A, D), (B, D) y (C,D) deben ocurrir juntos exactamente una vez para que exista un camino que cruza cada puente una y solo una vez.

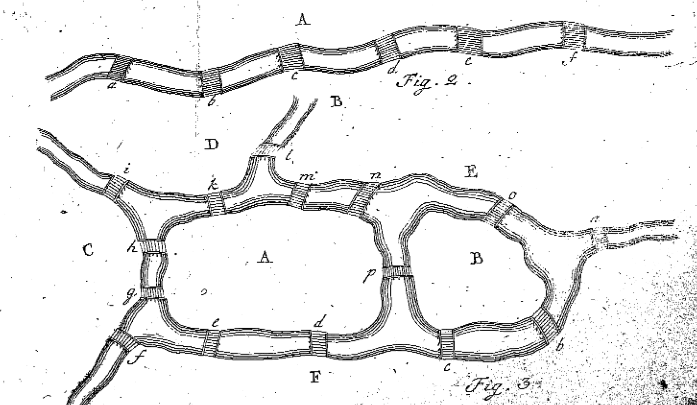
Figuras 2 y 3 de Euler de ‘Solutio problematis ad geometriam situs pertinentis,’ Eneström 53

En el párrafo 7, Euler informa al lector que necesita encontrar una secuencia de ocho letras que satisfaga el problema, o que necesita probar que no existe tal secuencia. Antes de hacer esto para el problema del puente de Königsberg, decide encontrar una regla para descubrir si existe un camino para un problema más general. Lo hace en el párrafo 8 mirando un ejemplo mucho más simple de masas de tierra y puentes. Euler dibuja la Figura 2 y comienza a evaluar las situaciones por las que se recorre la región A. Euler afirma que si el puente a se recorre una vez, A fue el lugar donde comenzó o terminó el viaje, y por lo tanto solo se usó una vez. Si los puentes a, b y c se recorren una vez, A se usa exactamente dos veces, sin importar si es el lugar de inicio o de finalización. De manera similar, si cinco puentes conducen a A, la masa de tierra A ocurriría exactamente tres veces en el viaje. Euler afirma que, » En general, si el número de puentes es cualquier número impar, y si se incrementa en uno, entonces el número de ocurrencias de A es la mitad del resultado.»En otras palabras, si hay un número impar de puentes que conectan A con otras masas de tierra, agregue uno al número de puentes y divídalo por dos, para averiguar cuántas veces en total se debe usar A en el camino, donde cada puente se usa una y solo una vez (p. ej. Ocurrencias totales de A donde A tiene un número impar de puentes = (#de puentes – 1) / 2).

Usando este hecho Euler resuelve el problema del puente de Königsberg en el párrafo 9. En ese caso, dado que hay cinco puentes que conducen a A, debe ocurrir tres veces (ver su Figura 1, arriba). De manera similar, B, C y D deben aparecer dos veces, ya que todos tienen tres puentes que conducen a ellos. Por lo tanto, 3(para A) + 2(para B) + 2(para C) + 2(para D) = 9, pero Euler ya declaró que solo debe haber ocho ocurrencias para los siete puentes. ¡Esto es una contradicción! Por lo tanto, es imposible recorrer los puentes de la ciudad de Königsberg una sola vez. El fin, ¿o es así? Mientras que la gente de Königsberg puede estar feliz con esta solución, el gran matemático Leonhard Euler no estaba satisfecho. Euler continúa con sus pruebas para tratar situaciones más generales.

Generalización de Euler

En el párrafo 10, Euler continúa su discusión señalando que si la situación involucra a todas las masas terrestres con un número impar de puentes, es posible decir si se puede hacer un viaje usando cada puente solo una vez. Euler afirma que si la suma del número de veces que debe aparecer cada letra es una más que el número total de puentes, se puede hacer un viaje. Sin embargo, si el número de ocurrencias es mayor que uno más que el número de puentes, no se puede hacer un viaje, como el problema del puente de Königsberg. Esto se debe a que la regla, que Euler da para un número impar de puentes, usando su Figura 2, es cierta para la situación general, ya sea que solo haya otra masa de tierra o más de una.

En los párrafos 11 y 12, Euler se ocupa de la situación en que una región tiene un número par de puentes unidos a ella. Esta situación no aparece en el problema de Königsberg y, por lo tanto, se ha ignorado hasta ahora. En la situación con una masa de tierra X con un número par de puentes, pueden ocurrir dos casos. El primer caso es cuando X es el punto de partida para el viaje. En este caso, X aparecerá dos veces, una vez como punto de partida y otra vez como punto final. En el otro caso, X no es el punto de partida. Si esto sucediera, X solo aparecería una vez, ya que el viaje tendría que entrar por un puente e inmediatamente salir por el único otro disponible. De manera similar, si hay cuatro puentes unidos a X, el número de ocurrencias de X depende de si es o no un punto de partida. Si el viaje comienza en X, debe aparecer tres veces, pero si no comienza en X, sólo aparecen dos veces. Por lo tanto, en general, si X tiene un número par de puentes unidos, entonces si el viaje no comienza en X, X aparece la mitad del número de veces que puentes (i. e. Ocurrencias de X donde X es par y no el punto de partida = (#de Puentes) / 2). Si el viaje comienza en X, entonces X aparece la mitad del número de veces que puentes, más uno (es decir, Ocurrencias de X donde X es par y punto de partida = ((#de puentes) / 2) + 1).

En los párrafos 13 al 15, Euler explica cómo averiguar si existe una ruta que usa cada puente una y solo una vez y presenta su propio ejemplo para mostrar cómo funciona. Euler primero explica su sencillo método de seis pasos para resolver cualquier situación general con masas de tierra divididas por ríos y conectadas por puentes. En primer lugar, Euler indica cada masa de tierra con una letra mayúscula. En segundo lugar, toma el número total de puentes, agrega uno y escribe esto sobre el gráfico que está a punto de hacer. A continuación, toma las letras mayúsculas, las coloca en una columna y, junto a ellas, escribe el número de puentes. Cuarto, indica con asteriscos las masas de tierra que tienen un número par de puentes. Luego, al lado de cada número par, escribe ½ del número y al lado de cada número impar coloca ½ del número más uno. Finalmente, Euler suma los números escritos en la columna de la derecha y si la suma es uno menor o igual al número de puentes más uno, entonces el viaje requerido es posible. Sin embargo, es importante tener en cuenta que si la suma es uno menos que el número de puentes más uno, el viaje debe comenzar desde una de las masas de tierra marcadas con un asterisco. Si la suma es igual al número de puentes más uno, el viaje debe comenzar en una región no marcada con un asterisco.

Ejemplos

Usando el problema de Konigsberg como su primer ejemplo Euler muestra lo siguiente:

Número de puentes = 7, Número de puentes más uno = 8

Región Puentes Debe aparecer la Región Veces

A 5 3

B 3 2

C 3 2

D 3 2

Sin embargo, 3 + 2 + 2 + 2 = 9, que es más de 8, por lo que el viaje es imposible.

Dado que este ejemplo es bastante básico, Euler decide diseñar su propia situación con dos islas, cuatro ríos y quince puentes. La situación creada por Euler se puede ver en su Figura 3, arriba. Euler ahora intenta averiguar si hay un camino que permita a alguien cruzar cada puente una vez y solo una vez. Euler sigue los mismos pasos anteriores, nombrando las cinco regiones diferentes con mayúsculas, y crea una tabla para comprobarlo si es posible, como la siguiente:

Número de puentes = 15, Número de puentes más uno = 16

Puentes de Región Debe Aparecer la región Veces

A* 8 4

B* 4 2

C* 4 2

D 3 2

E 5 3

F* 6 3

Además, 4 + 2 + 2 + 2 + 3 + 3 = 16, que es igual al número de puentes, más uno, lo que significa que el viaje es, de hecho, posible. Dado que la suma es igual al número de puentes más uno, el viaje debe comenzar en D o E. Ahora que Euler sabe que es posible hacer un viaje, todo lo que necesita hacer es indicar cuál será el camino. Euler elige el camino EaFbBcFdAeFfCgAhCiDkAmEnApBoElD, donde incluye los puentes que se cruzan entre las letras que representan las masas de tierra. Si bien esta información es extraña, ya que el puente exacto no importa para saber que un viaje es posible, es útil al seleccionar un camino. Este es un buen ejemplo que muestra el método que Euler usaría para resolver cualquier problema de esta naturaleza.

Conclusiones de Euler

En los siguientes párrafos, Euler presenta otra forma de averiguar si se puede hacer un viaje dado cualquier conjunto de masas de tierra, puentes y ríos. En el párrafo 16, Euler señala que el total de los números enumerados directamente a la derecha de las masas terrestres suma el doble del número total de puentes. Este hecho más tarde se conoce como el lema del apretón de manos. Básicamente, el lema de apretón de manos establece que cada puente se cuenta dos veces, una por cada masa de tierra a la que está unido. En el párrafo 17, Euler continúa afirmando que la suma de todos los puentes que conducen a cada región es par, ya que la mitad de este número es igual al número total de puentes. Sin embargo, esto es imposible si hay un número impar de masas terrestres con un número impar de puentes. Por lo tanto, Euler demuestra que si hay algunos números impares unidos a las masas de tierra, debe haber un número par de estas masas de tierra.

Sin embargo, esto no es suficiente para probar cuando hay un camino donde cada puente se usa una y solo una vez, ya que el problema del puente de Königsberg tiene un número par de masas de tierra con un número impar de puentes que van a ellos. Debido a ello, Euler añade más restricciones en los párrafos 18 y 19. Euler explica que, dado que el número total de puentes unidos a cada masa de tierra es igual al doble del número de puentes (como se ve en el lema de apretón de manos), por lo tanto, si agrega dos a esta suma y luego divide por dos, obtendrá el número total de puentes más uno. Este número es el mismo que el que se usó antes, que se usa para saber si un camino es posible. Si todos los números son pares, la tercera columna de la tabla sumará uno menos que el número total de puentes más uno.

Euler explica entonces que es obvio que si hay dos masas terrestres con un número impar de puentes, el viaje siempre será posible si el viaje comienza en una de las regiones con un número impar de puentes. Esto se debe a que si los números pares se reducen a la mitad, y cada uno de los impares se incrementa en uno y se reduce a la mitad, la suma de estas mitades será igual a una más que el número total de puentes. Sin embargo, si hay cuatro o más masas de tierra con un número impar de puentes, entonces es imposible que haya un camino. Esto se debe a que la suma de las mitades de los números impares más uno junto con la suma de todas las mitades de los números pares hará que la suma de la tercera columna sea mayor que el número total de puentes más uno. Por lo tanto, Euler acaba de demostrar que puede haber como máximo dos masas de tierra con un número impar de puentes.

Con esto dicho, Euler puede ahora hacer sus conclusiones sobre formas más generales del problema del Puente de Königsberg. En el párrafo 20, Euler da las tres pautas que alguien puede usar para averiguar si existe un camino usando cada puente una vez y solo una vez. En primer lugar, afirmó que si hay más de dos masas de tierra con un número impar de puentes, entonces ese viaje no es posible. Segundo, si el número de puentes es impar para exactamente dos masas terrestres, entonces el viaje es posible si comienza en una de las dos masas terrestres impares. Finalmente, Euler afirma que si no hay regiones con un número impar de masas terrestres, el viaje se puede realizar comenzando en cualquier región. Después de exponer estos tres hechos, Euler concluye su prueba con el párrafo 21, que simplemente afirma que después de que uno se da cuenta de que existe un camino, todavía debe hacer el esfuerzo de escribir un camino que funcione. Euler creía que el método para lograr esto era trivial, y no quería gastar mucho tiempo en él. Sin embargo, Euler sugirió concentrarse en cómo llegar de una masa de tierra a otra, en lugar de concentrarse en los puentes específicos al principio.

La prueba y teoría de grafos de Euler

Al leer la prueba original de Euler, uno descubre un trabajo de matemáticas relativamente simple y fácilmente comprensible; sin embargo, no es la prueba real sino los pasos intermedios los que hacen famoso este problema. La gran innovación de Euler fue ver el problema del puente de Königsberg de manera abstracta, mediante el uso de líneas y letras para representar la situación más amplia de masas de tierra y puentes. Usó letras mayúsculas para representar masas de tierra, y letras minúsculas para representar puentes. Este era un tipo de pensamiento completamente nuevo para la época, y en su artículo, Euler provocó accidentalmente una nueva rama de las matemáticas llamada teoría de grafos, donde un grafo es simplemente una colección de vértices y aristas. Hoy en día, un camino en un gráfico, que contiene cada borde del gráfico una y solo una vez, se llama un camino euleriano, debido a este problema. Desde el momento en que Euler resolvió este problema hasta hoy, la teoría de grafos se ha convertido en una rama importante de las matemáticas, que guía la base de nuestro pensamiento sobre las redes.

El problema del puente de Königsberg es por qué Biggs afirma,

Los orígenes de la teoría de grafos son humildes, incluso frívolos The Los problemas que llevaron al desarrollo de la teoría de grafos a menudo eran poco más que rompecabezas, diseñados para probar el ingenio en lugar de estimular la imaginación. Pero a pesar de la aparente trivialidad de estos rompecabezas, capturaron el interés de los matemáticos, con el resultado de que la teoría de grafos se ha convertido en un tema rico en resultados teóricos de una sorprendente variedad y profundidad.

Como implicaría la declaración de Biggs, este problema es tan importante que se menciona en el primer capítulo de cada libro de Teoría de Grafos que se examinó en la biblioteca.

Después del descubrimiento de Euler (o invención, dependiendo de cómo lo mire el lector), la teoría de grafos floreció con importantes contribuciones hechas por grandes matemáticos como Augustin Cauchy, William Hamilton, Arthur Cayley, Gustav Kirchhoff y George Polya. Todos estos hombres contribuyeron a descubrir » casi todo lo que se conoce sobre gráficos grandes pero ordenados, como la red formada por átomos en un cristal o la red hexagonal hecha por abejas en una colmena .»Otros problemas famosos de la teoría de grafos incluyen encontrar una manera de escapar de un laberinto o laberinto, o encontrar el orden de movimientos con un caballo en un tablero de ajedrez de tal manera que cada casilla se aterrice una sola vez y el caballo regrese al espacio en el que comenzó . Algunos otros problemas de la teoría de grafos han quedado sin resolver durante siglos .

El destino de Königsberg

Mientras que la teoría de grafos creció después de que Euler resolviera el problema del Puente de Königsberg, la ciudad de Königsberg tuvo un destino muy diferente. En 1875, la gente de Königsberg decidió construir un nuevo puente, entre los nodos B y C, aumentando el número de enlaces de estas dos masas de tierra a cuatro. Esto significaba que solo dos masas terrestres tenían un número impar de enlaces, lo que daba una solución bastante sencilla al problema. La creación del puente adicional puede o no haber sido causada inconscientemente por el deseo de un camino para resolver el famoso problema de la ciudad.

Sin embargo, un nuevo puente no resolvió todos los problemas futuros de Königsberg, ya que la ciudad no esperaba en el siglo XIX, «el triste y devastado destino que lo esperaba como anfitrión de una de las batallas más feroces de la Segunda Guerra Mundial.»Durante cuatro días en agosto de 1944, bombarderos británicos destruyeron tanto el casco antiguo como la parte norte de Königsberg. En enero y febrero de 1945, la región que rodea Königsberg está rodeada por fuerzas rusas. Los civiles alemanes comienzan a evacuar la ciudad, pero se mueven demasiado tarde. Miles de personas mueren tratando de huir en barco y a pie a través de las aguas heladas de la Laguna de Curlandia. En abril de 1945, el Ejército Rojo captura Königsberg con aproximadamente el noventa por ciento del casco antiguo en ruinas.

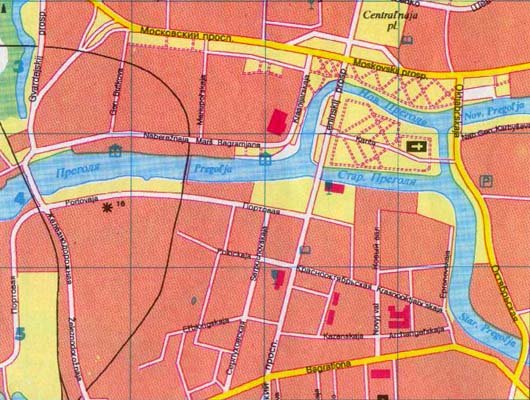
A continuación se proporciona un plano actual de Königsberg . Este mapa muestra cuánto ha cambiado la ciudad. Muchos de los puentes fueron destruidos durante los bombardeos, y la ciudad ya no puede hacer la misma pregunta intrigante que en el siglo XVIII. Junto con un diseño muy diferente, la ciudad de Königsberg tiene un nuevo nombre, Kaliningrado, con el río Pregel rebautizado Pregolya . Mientras que el destino de Königsberg es terrible, el viejo problema de la cafetería de los ciudadanos de atravesar cada uno de sus viejos siete puentes exactamente una vez llevó a la formación de una rama completamente nueva de las matemáticas, la teoría de grafos.

Biggs, Norman L., E. K. Lloyd, and Robin J. Wilson. Teoría de grafos: 1736-1936. Oxford: Clarendon Press, 1976.

Dunham, William. El Amo de Todos Nosotros. Washington: The Mathematical Association of America, 1999.

Euler, Leonhard,’ Solutio problematis ad geometriam situs pertinentis ‘ (1741), Eneström 53, MAA Euler Archive.

«History of Mathematics: On Leonhard Euler (1707-1783).»ScienceWeek (2003). 6 de noviembre 2005.

Hopkins, Brian y Robin Wilson. «La verdad sobre Königsberg.»College Mathematics Journal (2004), 35, 198-207.

«Konigsberg Bridges.»The MacTutor History of Mathematics Archive:
http://www-history.mcs.st – and.ac.uk/history/Miscellaneous/other_links/Konigsberg.html

Nota del editor: Este artículo fue publicado originalmente en Convergence, Volumen 3 (2006).