9. 임피던스 및 위상 각도
놓치지 마세요…
이 페이지의 뒷부분 애플릿에서 rlc 회로의 임피던스,전류 및 전압을 살펴보십시오.
임피던스
회로의 임피던스는 회로의 요소들의 조합에 의한 전류의 흐름에 대한 총 유효 저항이다.
기호:Z
단위: `Ω`
전체 전압에 걸쳐 모두 3 요소(저항,캐패시터,인덕터)록
VRLC
을 찾아 이 총계 전압,우리는 수 없습니다 단지 추가 전압 VR,VL 및 VC.
기 때문에 VL 및 VC 로 간주되는 상상의 수량으로,우리는 가지고 있습니다:
임피던스 VRLC=IZ
그렇게`Z=R+j(X_L−X_C)`
이제 크기(크기,또는 절대값)Z 에 의해 주어진:
`|Z|=sqrt(R^2+(X_L-X_C)^2`
단계 각
`탄\타=(X_L-X_C)/R`
각도 θ 나타내는 단계 사이의 각도 전류와 전압이 있습니다.
이것을 y=a sin(bx+c)의 그래프에서 이전에 만난 위상 각도와 비교하십시오.
실시예 1
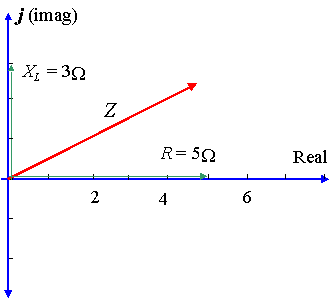
회로는`3\Ω`의 인덕터를 가로지르는 리액턴스와 직렬로`5\Ω`의 저항을 갖는다. 임피던스를 극 형태로 복소수로 나타냅니다.
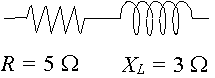
대답
이 경우에, `X_L=3\Ω`과`X_C=0`그래서`X_L-X_C=3\Ω`.
에서 이렇게 직사각형의 형태로,임피던스가 쓴:
`Z=5+3j\Ω`
를 사용하여 계산기의 크기 Z 에 의해 제공됩니다.`5.83`,그리고 각도`θ`(위상 차이)에 의해 제공됩니다.`30.96^@`.따라서 전압은 전류를’30 만큼 유도합니다.다이어그램과 같이 96^@’입니다.
Z 를 복소수(극성 형태)로 제시하면 다음과 같습니다.
`Z=5.83∠30.96^@\Ω`.
실시예 2(a)
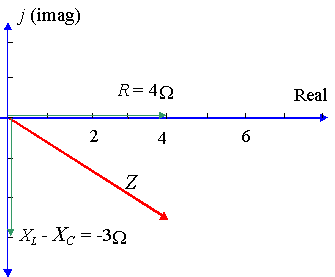
특정 ac 회로는`4\Ω`의 저항,`8\Ω`의 인덕터를 가로지르는 리액턴스 및`11\Ω`의 커패시터를 가로지르는 리액턴스를 갖는다. 회로의 임피던스를 극 형태로 복소수로 표현하십시오.
대답
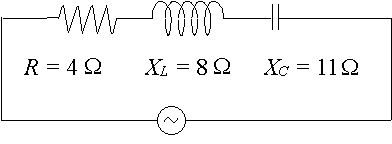
이 경우에,우리는: `X_L-X_C=8-11=-3\Ω`
그렇게`Z=4-3j\Ω 에서`직사각형의 형태이다.
이제 극성 형태로 표현하려면
계산기를 사용하여`r=5`와`θ=-36.87^@`를 찾습니다.
그렇게`Z=5∠-36.87^@\Ω`
대 RLC 그래프
아래는 대화형 그래프를 재생하는(그것은 정적인 이미지). AC 회로에서 총 임피던스에 대한 저항,커패시터 및 인덕터의 효과를 탐색 할 수 있습니다.
이 상호 작용에 대한 활동
- 첫째,그냥 슬라이더와 함께 재생할 수 있습니다. 당신은 할 수 있습니다:
끌어 최고 슬라이더 왼쪽 또는 오른쪽을 따라합 임피던스로 인해 저항기,`R`,
끌어 XL 슬라이더 또는 아래로 변화하는 임피던스로 인해 인덕터,`X_L`,그리고
끌어 XC 슬라이더 또는 아래로 변화하는 임피던스로 인해 커패시터,`X_C`. - XL−XC 및 Z 의 값에 대한 다른 임피던스의 영향을 관찰합니다.
- θ 에 대한 다른 임피던스의 효과,빨간색”결과”선이 수평(라디안)과 만드는 각도를 관찰하십시오.
- 대화식에서 전압 및 전류의 그래프를 고려하십시오. 슬라이더를 변경할 때 지연 또는 리드의 양을 관찰하십시오.
- 이 대화식으로 놀면서 무엇을 배웠습니까?