4 가지 색상 정리
4 가지 색상 추측은 150 년 만에 처음 언급되었으며 마침내 1976 년에 결정적으로 입증되었습니다. 그것은 오래된 아이디어가 새로운 발견과 어떻게 결합되는지에 대한 outstandingexample 이며,수학의 다른 분야의 기술은 새로운 문제를 제공합니다. 그것은 또한 방법의 예는 apparentlysimple 문제가 생각하는 해결’그러나 그 이후되었 morecomplex,그리고 그것은 첫 번째 멋진 예는 computerwas 에 관련된 증명하는 수학적 원리.
에서 시작
추측하는 모든 지도할 수 있 becoloured 를 사용하여 네 개의 색상 먼저 나타내는 편지에서 fromAugustus De 모건(1806-1871),첫 번째 수학 교수 atthe 새로운 대학 컬리지 런던,그의 친구 윌리엄 RowanHamilton(1805-1865)유명한 아일랜드에서 수학자 1852. 그것은 hadbeen 제안을 드건에 의해 하나의 자신의 학생들,FrederikGuthrie 를 대신하여,자신의 오빠 프랜시스(나중에 becameprofessor 의 대학에서 수학의 케이프타운).


아우구스투스 데 모건(1807-1871)andWilliam 웬 해밀턴(1805-1865)
문제,그래서 단순히 설명되지만,그렇게 어느때 difficultto 증명,의 상상력을 잡은 많은 수학자 thetime. 1860 년대 후반에 드 모르도 문제와 hisproof 미국 어디 다른 사람의 사이에서,벤자민 피어스(1809-1880)afamous 수학자 천문학에 관심이되었으로 그것을 거리를 개발하고 논리적인 방법입니다.
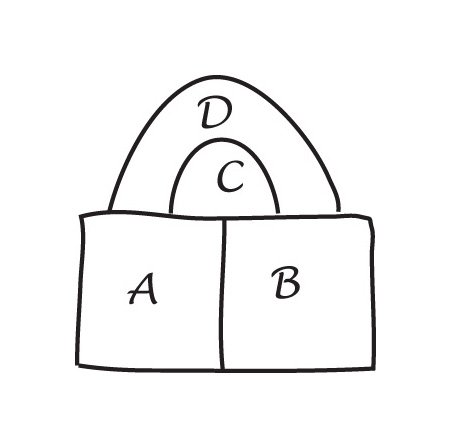
De Morgan 은 네 개의 지역이있는지도에서 각각다른 세 개를 터치하면 그 중 하나가 theothers 에 의해 완전히 동봉됩니다. 그는 이것을 증명하는 방법을 찾을 수 없었기 때문에 그것을 사용했습니다.공리,기초그의 증거.
의 복사본을 드 Morgan’s originalsketch 에서 그의 편지를 해밀턴과 간단한 네 가지 컬러 지도입니다.
1878 년에 아서 케일리(1821-1895)회의에서의 LondonMathematical 사회 여부를 묻는 사람이 있었다 해결책을 발견 forDe 모건의 원본 질문,하지만 거기에 있었다 someinterest,아무도 만들었다 어떤 중요한 진행됩니다. 케일 becameinterested 에서 문제가 및 1879 년에 발표했는 짧은 paperOn 의 채 mapswhere 그는 몇 가지 설명의 어려움에서도 proofand 몇 가지 중요한 기여하는 방법으로 문제가 wasapproached. 특정지도가 이미 4 가지 색상으로 채색되어 있고 다른 영역을 추가하면 여전히 동일한 채색을 유지할 수 있습니까?’의 또 다른 라인을 시작했다.문제에 대한 mathematicalinduction 의 응용 프로그램을 주도했습니다.

Arthur 케일리(1821-1895)
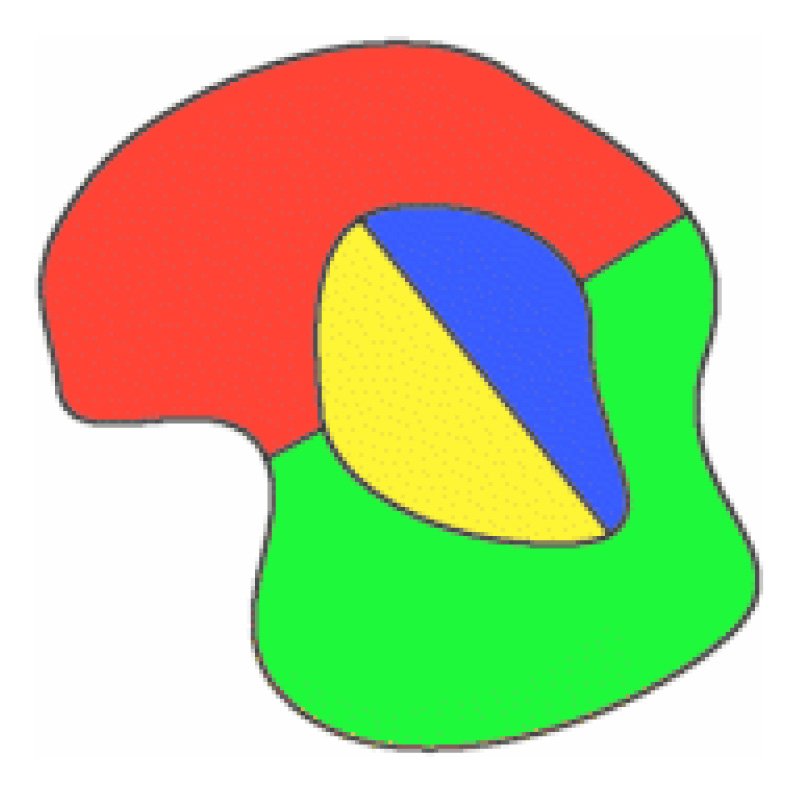
Arthur 케일을 보였는 경우 fourcolours 이미 사용하여 컬러 지도,새로운 지역 wasadded,그것은 항상 가능하지 않을 유지하 originalcolouring.
위의 네 가지 색상이 모두 원본지도에 사용되었으며 주변을 둘러싸기 위해 새롭게 지역이 그려져 있습니다. 이 경우 빨간색 영역이 파란색으로 바뀌므로 새 surroundingregion 에서 빨간색을 사용할 수 있습니다.
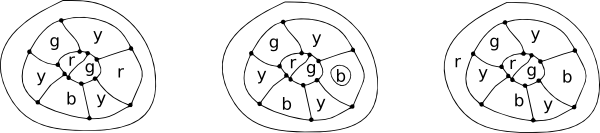
Cayley 는 또한 경계가 만나는 방식을 제한함으로써 버전 문제를 해결할 수 있음을 관찰했습니다. 예를 들어,단지 3 개국이 만난지도에는 avertex 에서 만나는 3 개의 가장자리가 있습니다. 이들은’큐빅 맵’이라고하며,토론에 사용 된 맵은 모두 큐빅 맵입니다. 또한지도가 될 수있는 경우 4 가지 색상으로 채색하면 3 가지 색상 만 표시됩니다.
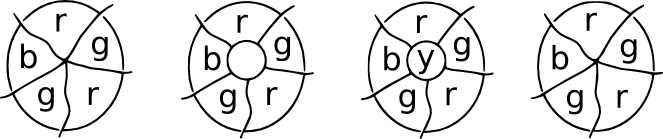
패 데모입니다. 상상해 보라.지도의 어떤 곳에서는 여러 국가가 한 지점에서 만난다. 이제 회의 지점 위에 패치를 붙이고 모든 새 회의 지점에는 세 개의 테두리가 있습니다. 이것들은 큐빅 맵이며,네 번째 색상은 중앙 영역에 사용될 수 있습니다. 제거시패치,우리는 원래의 색소로 돌아갈 수 있습니다.
오래된 기술,새로운 조건 및 더 많은 문제!
문제의 발전을 따르기 위해서는 수학자가 그것을 해결하려는 시도에서 개발 한 아이디어,절차 및 기술 중 일부를 간략하게 설명해야합니다.
유일한 다섯 이웃을 추측
‘해결할 수 없는 경우 특정 문제를 찾아보다 쉽게 해결할 수 있다.'(폴리아. 그것을 해결하는 방법)
‘모든지도는 적어도 onecountry 와 몇몇 이웃니다.’
바다로 둘러싸인 섬의지도를 상상해보십시오. 섬의 나라의 색채에서,우리는 바다를 하나로 계산합니다.지역. 일부 국가는 두 가지경(a digon),somethree(으로 삼각형),일부 four(사각형)그리고 일부는 다섯 가지(apentagon)나 더 있습니다.
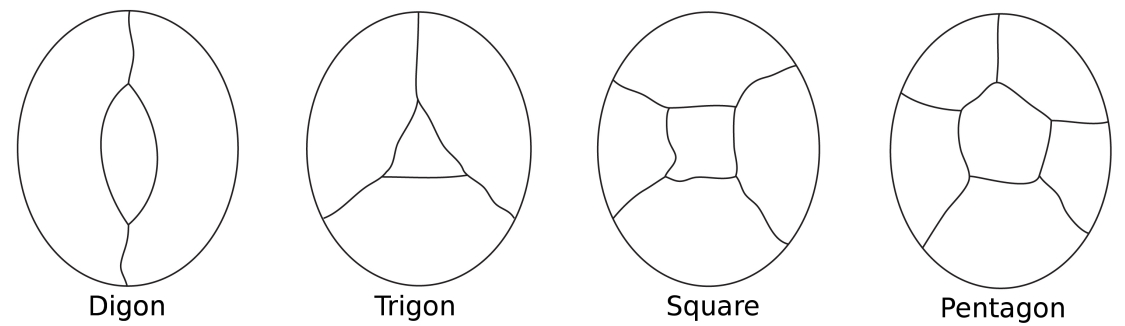
간단한 possibleconfigurations 주변 중심 지역이다.
이러한 모든 구성에서 각 노드에는 3 개만 있습니다.
1813 년에,다면체에 대한 오일러의 공식은 Augustin Cauchy(1759-1857)가 다면체를 평면에 byprojecting 하여 thesolid 의 그물을 형성함으로써 2 차원에 대해 적용되었다. 이 방법으로 수식은$f+v-e=1$가되었는데,그물의’외부’영역을 계산하지 않았기 때문입니다.

어거스틴 코시(1759-1857)
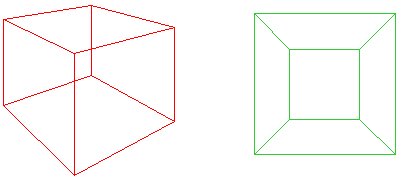
상상을 부수 빨간 큐브 downonto 비행기는 그것의 기초가 열식 outsideedge 의 녹색 net. Cauchy 의 아이디어는 평면 다각형의 경우$f+v-e=1$가되도록 thecube 의 한면을 잘라내는 것이 었습니다. 또한’외부’의 순으로 간주된 얼굴로 infinitearea,그리고 우리는 아직$f+v-e=2$
우리가 추측할 수 있는 적어도 세 가지 테두리라인(가장자리)에서 나오는 각 회의 포인트(꼭지점).
지도에 둘러싸인 적어도 하나의 국가가 있다는 증거 5 개 이하의 이웃은 모순으로 진행됩니다. 이것이 부조리로 이어진다면,우리는 증거를 가지고 있습니다.
이제이 값을 오일러의 공식에 넣으십시오.$$f+v-e=2$$andwe 는$$1/3(e)+2/3(e)-e$$0 입니다!
이것은 부조리,그래서 우리의 원래 가정은 거짓이었다.즉,5 명 이하의 이웃이있는 한 국가가 있어야합니다!
최소한의 범죄자!
4 가지 색상 문제를 해결하는 또 다른 방법은 isfalse 라고 가정하고 이것이 어디로 이어지는지 확인하는 것입니다. 필요한지도가 있다고 가정합니다.5 가지 색상 이상,그리고 우리는 가장 작은 국가 수를 가진지도를 선택합니다. 이러한지도를 최소 카운터 예 또는미니멀 범죄자!
이것이 의미하는 최소한의 범죄할 수 없습 색깔을 가진 네 가지 색상이지만,어떤 지도 몇몇 국가할 수 있습 색깔을 가진 네 가지 색상입니다. 우리가 최소한의 범죄자가 존재할 수 없다는 것을 보여줄 수 있다면,우리는 약간의 진전을 이룰 수있을 것입니다.예를 들어,우리는 최소한의 범죄자가 디곤을 포함 할 수 없다는 것을 보여줄 수 있습니다.
원래지도에서 digon 에서 경계를 없애고우리는 더 적은 수의 국가로 새로운지도를 얻습니다. 이지도는 색상 일 수 있습니다.네 가지 색상으로(우리의 가정에서). 그런 다음이 newmap 을 색칠합니다(두 가지 색상 만 필요함). 이제 우리가 제거한 테두리를 교체하고지도를 다시 채색하십시오. 우리가 사용되는 세 가지 색상,그리고 이후에 thereis 여전히 하나 더 많은 색상을 사용할 수 있는 것을 보여줍 우리의 지도할 수 있습 becoloured 네습니다. 그러나 이것은 우리의 가정에 어긋나므로 최소한의 범죄자는디곤을 포함합니다.
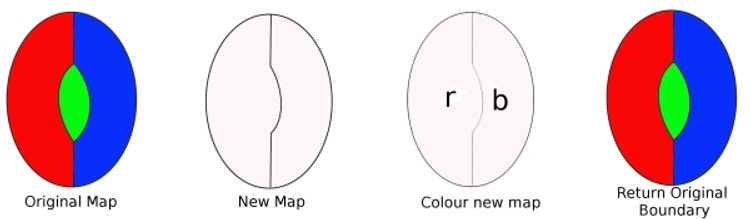
한다는 것을 보여주는 최소한의 Criminalcannot 을 포함 지역으로 두 개의 가장자리(a digon). 거기에 있다고 가정 해보십시오.digon 이 포함 된 최소한의 범죄자. 가장자리 제거는지도에 더 적은 수의 영역이 포함되어 있음을 의미합니다. 그래서이 새로운지도는 색상 일 수 있습니다.네 가지 색상으로. 이제 잃어버린 가장자리를 교체하십시오. 이후에만 twocolours 었기 전에 필요한 교체,가장자리미 우리가 사용할 수 있습니다 athird 컬러,그리고 아직도 네 번째는 컬러를 사용. 그래서,최소한의 크리미널은 네 가지 색상으로 채색 할 수 있습니다. 따라서 minimalcriminal 은 digon 을 포함 할 수 없습니다.
이 절차를 반복될 수 있다는 것을 보여주는 최소한의 criminalcannot 포함 three-sided 국가(a 곤)지만,그것은 휴식 downwhen 우리는 시도하는 기술에 광장,기 때문에 우리가 대체 thesquare,국가는 다음을 수을 사용하여 모든 fourcolours,그렇게 증거 절차가 실패합니다. 일단 이것이 일어나면,그것은오각형을 위해 작동하지 않을 것임이 분명합니다.
여섯 가지 색 정리
비슷한 기법을 적용하여 여섯 가지 색칠이 참임을 보여줄 수 있습니다. 첫째,우리는 할 수있는지도가 없다고 가정합니다.6 가지 색상으로 채색됩니다. 일부의 지도할 수 있습 색 withseven 색상,그 중 하나를 선택하는 이(최소한의 범죄),ifwe 할 수 있는 표시 가능하다는 색상으로 sevencolours,우리가 달성한 우리의 목표입니다.
다섯 이웃 정리의 증명에서,그것은 가능합니다최소 범죄 아이디어를 사용하여 어떤지도도 육색으로 채색 될 수 있음을 보여줍니다!
지역에서 매듭,네트워크 토폴로지
1879 년에는 알프레드 Kempe(1849-1922),사용하는 기법과 유사 tothose 위 설명에서 시작은’다섯 개의 이웃산 ‘and 절차를 개발로 알려진 방법을의’에 위치하고 체인’tofind 증거 네 가지의 색상 정리했습니다. 그는이 증거를미국 수학 저널. 그는 두 가지 간단한 versionsthat 출판되었다,다음 해에 그의 증거에 대한 서 tenyears 기 전에 퍼시 Heawood(1861-1955)을 보였었습 animportant 에 오류가 증명하는 방법에 위치하고 사용했다.


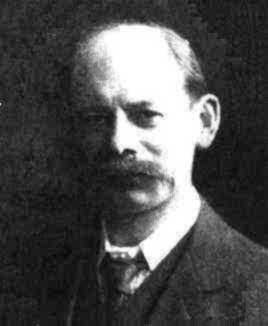
알프레드 Kempe(1849-1922),PeterGuthrie Tait(1831-1901)및 퍼시 Heawood(1861-1955)
1880 년에 P.G.Tait(1831-1901)수학 물리학자, offereda 솔루션하는 문제입니다. 독립적으로 Tait 설립했 thatmaps 는 짝수의 경계선에서 만나는 모든 지점이 될 수 있 색상의 두 개의 색상이지만,이 결과 hadappeared 이전에 위치하고의 논문입니다.
1876-77 년 동안 Tait 는 그의 연구 및 매듭의 분류로 잘 알려졌습니다. 그 당시에는 여러 가지가있었습니다.원자의 구조에 관한 다른 이론. 윌리엄 톰슨(후,켈빈 1824-1907)실험에서 영감을의 theGerman 물리학자 헤르만 폰 Helmholtz(1821-1894)제 atheory 는 원자 했 매듭 관다. 켈빈의’vortex atoms’이론은 약 20 년 동안 진지하게 받아 들여졌으며,그것은 매듭의 분류를 수행하기 위해 Tait 에게 영감을주었습니다. Tait,Thomsonand James Clark Maxwell(1831-1879)은 많은 토폴로지 아이디어를 발명했습니다.그들의 연구. 그러나 켈빈의 이론은 근본적으로미스타킹과 물리학 자들은 타이트의 작품에 관심을 잃었다.


헤르만 폰 Helmholtz(1821-1879),켈빈(1824-1907)스 클라크 맥스웰(1831-1879)

Tait 과 함께 시작되었는 방법에는 단 폐쇄 루프 코드의 수 있 매듭. 그는 체계적이지 않았습니다.시작시 asingle closed loop 를 가져 와서 매듭을 짓는 방법을 실험함으로써 직관적 인 방법으로 시작했습니다. 물론,코드는 열려 있어야했습니다(ashoelace 와 같이)그런 다음 매듭을 짓고 합류했습니다. 매듭 주위의 코드를 따라 가면’오버 언더’횡단이 번갈아 나타납니다.그는 그 다음 두 개의 루프와 함께 매듭 될 수있는 방법을 실험하기 위해 계속되었습니다. 여기에 표시된 것은 최대 6 개의 매듭입니다.단일 루프에 대한 크로싱.
Tait 의 연구 결과 중 하나는 그의 해밀턴 그래프 추측이었다.지도는 구에 그려진 다면체로 간주되며 평면에 투영 될 수 있습니다. Tait 는 어떤 입방체라도 제안했습니다.polyhedral 지도에는 Hamiltoniancycle 이 있습니다. Tait 의 방법은 그래프의 가장자리에 초점을 맞추 었습니다.그는 해밀턴 사이클이 4 색 ofa 맵을 생성 할 수 있음을 보여주었습니다. 윌리엄 투트(1917-2002)가 발견 한 것은 1946 년까지는 아니었다.타이트의 추측에 대한 첫 번째 반례.
Tait 와 매듭과의 연결
Taitinitiated1880 년에 snarks 의 연구를 수행했을 때,fourcolour 정리는 snark 가 없다는 진술과 동등하다는 것을 증명했다. 평면 그래프는 평면에서 그릴 수있는 그래프입니다.가장자리가 교차하지 않습니다. 마치 타이트의 평면이 아닌 graphsmight 에 대한 생각이 매듭과 해밀턴 경로에 대한 그의 연구에서 나온 것처럼 보입니다.
첫 번째 알려진 문을 열었는데 그래프에서 발견 1898,수학자들을 사냥하기 시작했 더 많은 이러한 종류의 graphsbut 지 1946 년까지는 또 다른 문을 열이 발견되었다.
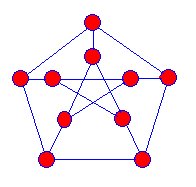 |
Snarks 은 예측의 세 가지 차원 그래프에 theplane. 파란색 가장자리가 다른 쪽을 가로 지르는 것처럼 보이는 꼭지점은 없습니다. Snarks 는 다음과 같은 속성이 있습니다.
|
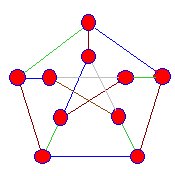 |
가장자리가 회의의 정점이 문을 열은 청색,녹색,갈색,하지만 우리는 항상는 단계에 도달 이 processcannot 는 계속되어야 합니다. |
줄리어스 피터슨(1839-1910)
사냥의 theSnark 시에 의해 작성 Lewis Carroll,그리고 마틴 Gardnernamed 이러한 그래프를 Snarks, 기 때문에 그들은 그렇게 어려운 것입니다.
문제를 변형시키고 새로운 방법을 찾는다.
지만 Heawood 발견 주에 위치하고 있음을 증명 방법 in1890 하지 못했에 가서 네 가지를 증명하는 컬러 정리,buthe 상당한 돌파구하고 결정적으로 입증 thatall 맵 수 colouredwith 다섯습니다.
Heawood 는이 문제에 많은 중요한 공헌을하여지도의 영역에서 관심의 초점을 그들 사이의 경계로 옮겼습니다. 1898 년까지 그는 각 지역 주변의 개수가 3 개로 나눌 수 있다면 지역이 4 가지 색상으로 채색 될 수 있음을 증명했습니다.
코시의 증거의 오일러의 공식 포함한 아이디어 thatany net 의 다면체할 수 있습 삼각을 추가하여 가장자리를 makenon-삼각형의 면으로 삼각형입니다. 그런 다음 절차를 개발했습니다.가장자리를 하나씩 삭제하여 각 단계에서 오일러 포뮬러가 유지 될 수 있음을 보여주었습니다.
코시의 증거의 오일러의식을
코시의 1813 증거의 오일러의 수식으로 시작의 아이디어 aprojection 의 다면체를 구하는 비행기들을 net. 그는(a)그물이 삼각 측량 될 수 있다는 것을 증명했으며,오일러의 공식에 대한 그의 증거(b)는 당시에 받아 들여졌다.
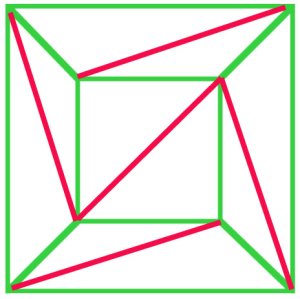 (a)
|
In principle, every polygonal net can be triangulated. In thisnet of a cube (a), $f + v – e$ is $10 + 8 – 17 = 1$, and Euler’sformula still holds. |
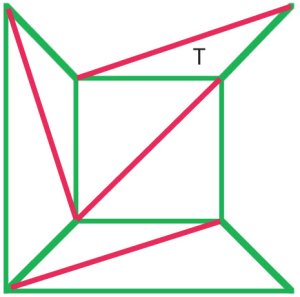 (b)
|
코시의 인수를 제거하는 외부 가장자리 에서 다이어그램(a)하나씩,그리고 때 그는 단계에 도달으로 다이어그램(b)제 온 삼각형 T,따라서 유지 오일러의 공식입니다. 19 세기 초반의 많은 사람들이절차는 allpolyhedra 에 대한 오일러의 공식의 증거를 보여 주었다. |
1900,수학자들이 알고 있는 평면 그래프의 수 있습 beconstructed 에서 모든 지도를 사용하여 강력한 개념의 이중성. 이중에서,theregions 는 꼭지점으로 표시되고 두 개의 꼭지점은 영역이 인접한 경우 가장자리에 의해 결합됩니다. 이 그래프에서 FourColour 추측은 이제 그래프의 꼭지점이 인접한 두 꼭지점이 thesame 색상이되지 않도록 4 가지 색상으로 칠할 수 있는지 묻습니다.
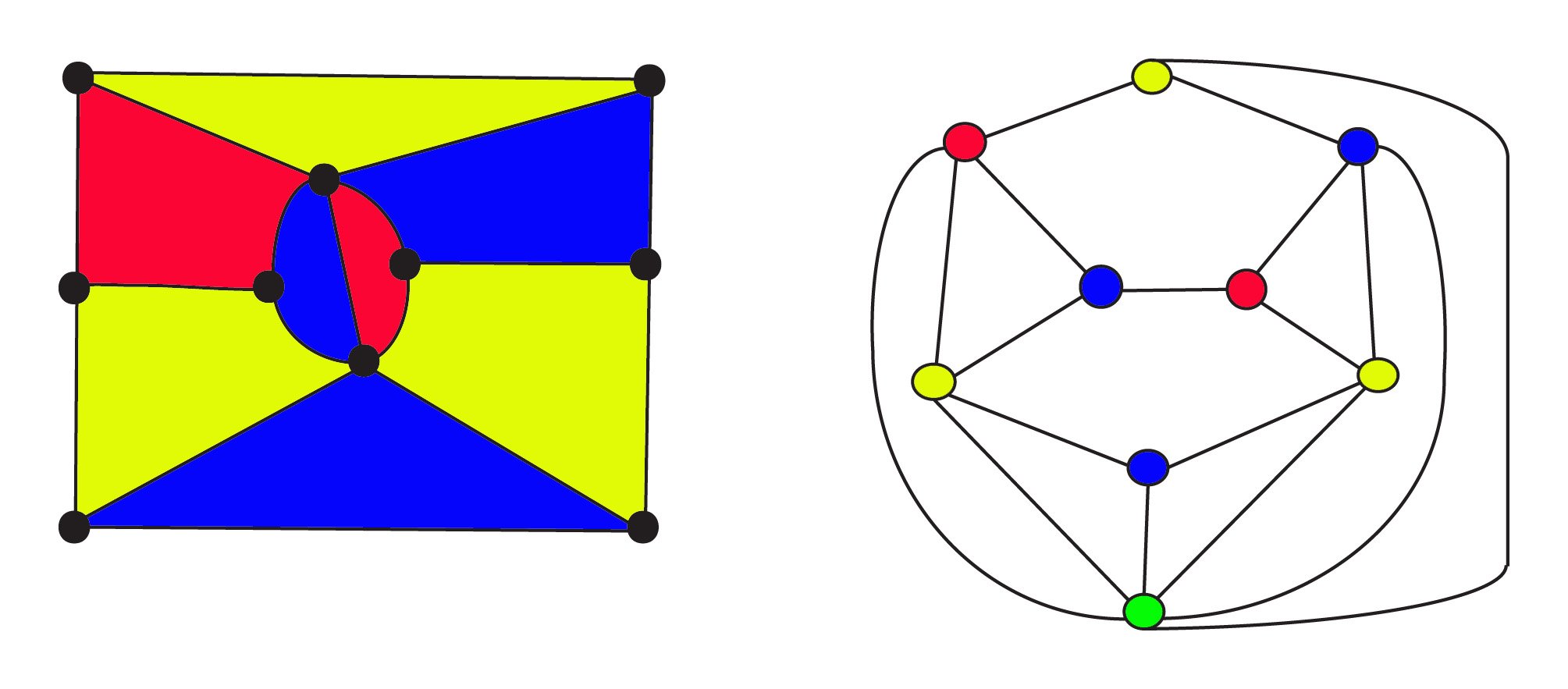
3-컬러 지도 왼쪽에 있는$8$지역$10$꼭지점과 17 달러$가장자리입니다. Theright 의 이중 그래프에는$9$지역$9$꼭지점과$17$가장자리가 있습니다. 그래프의 하단에있는 greenvertex 는지도에 대한 무한 externalarea 를 나타냅니다. 원래 지도하고 이중에 순종 오일러 ‘sFormula 네트워크$f+v-e=1$거나,$\text{지역}+\text{vertices}-\text{가장자리}=1$. 이중성 관계는대칭:이중의 이중은 원래 그래프가 될 것이며,여기서 정점과 정점이 교환됩니다.
의 전반 도중기,mathematiciansfocused 에서 수정하여 이러한 종류의 기술을 reducecomplicated 지도 특별한 경우에는 식별할 수 있습 andclassified 을 조사하기 위해,자신의 특정 속성을 anddeveloped 의 아이디어를 최소한의 지도 구성 thatcould 테스트 할 수 있습니다.
첫 번째 인스턴스에서,세트 생각되었을 포함 nearly9,000 멤버들이었다 거대한 작업,그리고 mathematiciansturned 을 컴퓨터 기술을 쓰는 알고리즘을 할 수 있 thetesting 니다. 알고리즘은 Kempe 의 수정 된 버전을 사용했습니다.체인의 원래 아이디어는 최소 세트의 멤버 수를 줄이기 위해 다른 기술과 함께 사용됩니다.
과 협력 후 요한 코크에 문제가 ofreducibility,1976 년에 일리노이 주립대학교 케네스 Appeland 볼프강 하켄 결국 감소의 시험 문제를 anunavoidable 으로 설정 1,936 구성,완전한 solutionto 네 가지 컬러 추측했습니다. 맵의 환원성을 하나씩 확인하는이 문제는 다른 프로그램과 다른 컴퓨터에서 두 번 확인되었습니다. 들의 증거 showedthat 적어도 하나의 지도와 함께 가장 작은 수 regionsrequiring 가지 색상의 존재할 수 없습니다.
첫 번째 증명 이후보다 효율적인 알고리즘이 발견되었습니다.4-채색지도와 1994 년까지 피할 수없는 집합은 633 으로 줄어 들었습니다.
컴퓨터에서 수행 된’증거’는 적절한 증거입니까?
증명은 컴퓨터의 도움으로 이루어 졌기 때문에 즉각적인 항의가 있었다. 많은 수학자들과 철학자들이 주장했다.그 증거는 합법적이지 않았습니다. 일부했다는 증거 shouldonly 것’입증’의 사람들도 아니고,기계,하는 동안,다른 사람의 morepractical 마음의 신뢰성에 의문을 제기 모두 algorithmsand 의 능력을 기를 수행하지 않고 오류가 있습니다.그러나 수학자가 작성한 많은 증명은 결함이있는 것으로 밝혀 졌으므로 신뢰성에 대한 논쟁이 비어있는 것처럼 보입니다.표현 된 의견이 무엇이든,상황은 심각한 결과를 낳았습니다.오늘날에도 여전히 계속되는 증거의 본질에 대한 비난.
교육학 노트:
이 기사 상단의 메모 탭을 사용하거나 여기를 클릭하십시오.
노트
- 이것과 이것에서 발견 된 다른 절차에 대한 자세한 내용은 Robin Wilson 의 책에서 볼 수 있습니다 네 가지 색상이 충분합니다.
- 매듭할 수 있습 왼손잡이나 오른손잡이,그리고 오늘이 명심해야 할 사항입 응용 프로그램의 이 숙박 시설에서 화학,약학,생물학,물리학입니다. (교육학 노트 참조)
- 윌리엄 로완 해밀턴(1805-1865)의 이름을 따서 명명되었습니다. 그래프의 해밀턴 경로 방문각 꼭지점은 정확히 한 번입니다. 해밀턴 사이클(또는 회로)은 각 정점을 정확히 한 번 방문하여 정점으로 되돌아가는 냉담합니다.(참조:교육학 노트)
- 이 책에 의해 부 Lakatos,교정이고 반론은 adiscussion 고 비판의 코시의 절차(페이지 6-12),대부분 더 많은 이야기에의 오일러의 정리했습니다.
- 이중성의 아이디어는 16 세기와 17 세기에 일어났습니다.투영 기하학의 발전. Pascal 과 desargues 와 같은 수학자들은 특정 geometricalconfigurations 에 대한 설명에서 theterms’point’와’line’을 교환하여 새로운 정리를 찾을 수 있음을 발견했습니다. 예는 규칙적인 다면체에 있습니다.하나의 정점은 다른면의 얼굴에 해당합니다. 그래서 사면체의 이중 면체는 또 다른 사면체이며,입방체의 이중 면체는 8 면체입니다. 이중의 이중은 원본입니다.폴리 면체.
최고의 인기,읽기 쉬운 책이에 네 ColourTheorem 가:
Wilson,R.(2003)
네 가지 색상으로 충분합니다.
런던. 펭귄 책.
에 대해 더 상세한 기술의 역사,standardreference 책입니다:
빅스,N.;Lloyd,E.&Wilson,R.(1986)(1998 년)
그래프 이론,1736-1936
옥스퍼드도 있습니다. 옥스포드 대학 출판부.
이 하나는 더 최근의 기초와 함께 우리에게 최신 정보를 제공합니다.
Fritsch,R and Fritsch,G(2000)
4 가지 색 정리:역사,토폴로지 기초 및 증거의 아이디어
뉴욕. 스프링거-Verlag.수학의 역사;AnIntroduction.
거의 모든 일반적인 역사는 책은 많은 주제에 대하지만,마지막 장에서츠’라는 컴퓨터 응용 프로그램’은 asection 에서는 그래프 이론,및 네 개의 색상 정리 mentionedtwice.
폴리아 G. 해결 방법.
이것은 문제 해결에 관한 고전적인 책입니다. 1950 년대에 처음 등장한 이래로이 책의 많은 판이 있었으며그것은 여전히 쉽게 사용할 수 있습니다. 흥미롭게도 최근 판은부제’수학적 방법의 새로운 측면’.
Lakatos,I.(1976)증명 andRefutations:수학적 발견의 논리.
캠브리지. C.U.P.
이 연구는 1970 년대에 toproblem 해결 및 조사를 주도 또 다른 중요한 책이다. 을 시작으로 aclassroom 토론을 사이에 교사 그리고 그룹의 studentsabout 증거의 오일러의 수식,그리고 범위를 통해서 아이디어,반대하는 가능성을 실제로 논의 bymathematicians 고 과학자들됩니다. 그것은 교육 및 학습에 관한 가장 중요한 문제 중 일부입니다.문제 해결 및 수학적 방법 및 증거에 관한 문제.
관련 참고 문헌
나는 얼마 동안 문자열 게임에 관한 작은 책을 가지고 있었다. 학교에서 Iwas 가 고양이의 요람이라고 불렸을 때,우리는 우리의 시간에 그것을 연주했습니다.
최근에 프랑스 저널이 문자열 인물의’algebra’에 논문을 발표했습니다! 아마존에 가면 Ann Swain 과 Michael Taylor 가 Finger Strings:A Book of Cats Cradles andString Figures 라는 anice book 을 찾을 수 있습니다 September2008 의 Floris books 에 의해 출판 될 그림. 일부 80 수치를 설명한 컬러의 다이어그램.그것은 나선형의 바운드,그래서 그것이 열려 있는 동안 당신은 지침을 따릅. 또한 몇 개의 문자열 루프가 함께 제공됩니다!
매듭 전문가를 위해,매듭의 AshleyBook 는 매듭의 다른 종류 및 그들의 용도의 thehundreds 에 흥미있는 누군가를 위해 고전이다. 아마존은다른 가격으로 제공되는 다양한 에디션.
웹 링크
에 대한 일반적인 개요를 링크하는 많은 사람들이 주제,theMacTutor 웹사이트
그리고 물론 MacTutor 전기 관련된 사람들의 indeveloping 다른 모든 수학적 측면을 찾을 수 있습니다 atthe MacTutor 전기 Index.
네 가지 색 정리와 세 가지 증명. 에 대한 mathematicallypersistent 은 다음 웹 사이트 흥미로운 새로운 접근 방식 toattacking 의 문제를 새로운 생성 알고리즘에 대한 solvingthe 문제,그리고 매는 줄에 대한 의존도 컴퓨터가 있습니다.http://www.emu.edu.tr/~cahit/the%20four%20color%20theorem%20—%20three%20proofs.htm
에 대한 그래프 이론,위키피디아 좋은 개요를 제공합,그리고 당신은 canskip 정말 기술적인 물건입니다. 그것은 현대의 종류를 보여줍니다.이 수학 영역의 응용 프로그램. Graphcoluring 으로 이동하여 4 가지 색상 정리를 클릭하면 찾을 수 있습니다.더 많은 정보.
매듭 이론의 흥미롭고 너무 기술적 인 역사-켈빈의 물리학에서 아이디어가 원자 이론으로 돌아가는 방법오늘.
수학 교사 협회에는 셀틱 Knotdesign 포스터가 있습니다. 그들의 웹 사이트로 이동하여 알파벳을 탐색하십시오.자원 목록.
매듭 아틀라스에서 매듭에 대한 모든 것을 알아보십시오! 하지 않은 경우 anexpert-그냥을 즐길 수 있는 다양하고 복잡한 데이터베이스의”에서의 영 wiki”
더 예술적이고 다채로운이지만,적은 수학은 theKnot 줄거리이다.
고 싶은 사람들을 위해 몇 가지 원래의 물건과 historicaldetail 이동하는 역사의 매듭이론