편집자 주

다음과 같은 학생들의 연구 보고서 준비한 교수 Judit Kardos’수학 255 클래스 개최,대학에서의 새로운 저지입니다. 이것은 수학의 역사에서 3 학점 입문 과정이었습니다. 이 보고서는 최종 등급의 30%로 계산되었습니다. 그것은 학생들이 보조 소스를 사용하여 할 수있는 일종의 역사 연구의 예입니다.

레너드의 오일러의 솔루션을 쾨니히 스 베르크리에 문제가

Konigsberg

우리의 이야기가 시작에서 18 세기에서의 기이 한 마을 쾨니히 스 베르크,프로이센의 은행에 Pregel River. 1254,게르만 기사의 도시를 설립했 쾨니히 스 베르크에서 이끌어의 보헤미안 왕 Ottoker II 후에 자신의 두 번째 성전에 대한 프러시아군. 중세 시대에 Königsberg 는 강가에 전략적으로 자리 잡은 매우 중요한 도시이자 무역 중심지가되었습니다. 작품에서 여덟 세기를 보여줍 쾨니히 스 베르크로 번영하는 도시,어디에 선박의 함대를 채우기 Pregel,그리고 그들의 무역 제공 편안한 라이프 스타일을 모두 지역 상인과 그 가족. 건강한 경제가 허용된 사람들의 도시를 구축하는 세븐 브리지,강을 건너 대부분의 섬과 연결되어의 Kneiphof;그들의 위치를 볼 수 있습에서 첨부된 그림입니다.

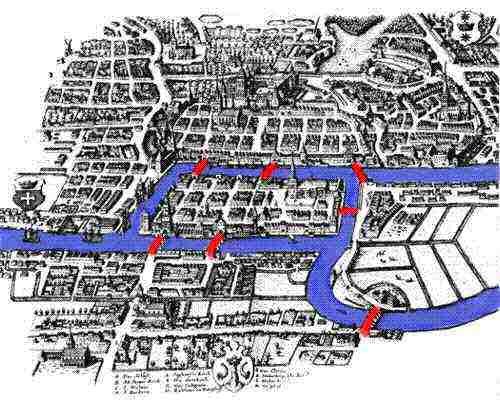
로 강이 흘러 주 Kneiphof,그 의미 pub 야드,및 다른 섬,그것은 모양으로 뚜렷한 영역입니다. 세븐 브리지었다라는 대장장이의 다리를 연결하는 다리,그린 브리지,상인의 다리,나무리 다리,그리고 꿀에다. Lore 에 따르면,Königsberg 의 시민들은 일요일 오후를 그들의 아름다운 도시를 산책하는 데 사용했습니다. 걷는 동안,도시의 사람들기로 결정을 게임을 만들에 대한 자체,그들의 목표는 것을 고안하는 방법에 그들은 도시 주변 산책,횡단 각각의 일곱 교량습니다. 도의 아무도 시민들에 쾨니히 스 베르크를 발명할 수 있는 경로는 것이 그들을 십자가 각각 다리를 한 번만,여전히 그들이 없었다는 것을 증명하는 것은 불가능한 일이었습니다. 그들에게 운이 좋았던 Königsberg 는 유명한 수학자 Leonard Euler 의 고향 인 St.Petersburg 에서 너무 멀지 않았습니다.

오일러와 다리 문제

오일러는 왜 수학 분야와 무관 한 문제로 자신을 염려합니까? 왜 그런 위대한 수학자가 쾨니히 스 베르크 다리 문제와 같은 사소한 문제로 많은 시간을 할애 할 것입니까? 오일러는 평생 동안 500 권 이상의 책과 논문을 출판하면서 분명히 바쁜 사람이었습니다. 1775 년에 혼자서,그는 평균의 하나는 수학 용지는 주당,그리고 그의 일생 동안 그가 쓴에 다양한 항목 외에 수학을 포함하여 기계,광학,천문학,탐색,그리고 유체역학. 그것은 놀라운 일이 아닙 오일러 느낌이 문제,사소한 진술서 1736 편지 레온하르트 칼 Gottlieb Ehler,시장의 찌히는 그에게 물었다한 문제에 대한 해결책:

. . . 따라서 당신은,가장 고귀한 선생님,어떻게 이런 유형의 솔루션을 맺은 관계를 수학,그리고 내가 이해하지 못하는 이유를 기대할 수학자를 생산하는 it,보다는 오히려 다른 사람에 대한 솔루션을 기반으로 혼자 이유로,그리고 그것의 발견에 의존하지 않는 어떤 수학적 원리입니다. 이 때문에,내가 왜 몰라도의 질문에는 부담 그래서 작은 관계를 수학하는 해결이 더 빠르게 수학자들에 의하여 보다 다른 사람입니다.

지만 오일러 발견 사소한 문제,그는 여전히 음모를 꾸몄습니다. 보낸 편지에서 동해 Giovanni Marinoni,이탈리아의 수학자 및 엔지니어,오일러는 말했다,

이 질문은 너무 평범하지만,나에게 보였의 가치 관심에서는 형상으며,대수학,심의 예술을 계산하는 데 충분한 해결합니다.

오일러 믿은 이 문제와 관련된 주제리프트 Wilhelm Leibniz 면 논의와 갈망하는 작품으로,무언가를 Leibniz 라 geometria 세도나 형상의 위치입니다. 이 소위 위치 기하학은 이제 오일러가이 유명한 문제를 해결하면서 소개하고 활용하는 그래프 이론이라고 불리는 것입니다.

오일러의 증명

1735 년 8 월 26 일 오일러는 쾨니히 스 버그 다리 문제에 대한 해결책을 담은 논문을 제시합니다. 그는이 특정 문제뿐만 아니라 임의의 수의 landmasses 및 임의의 수의 브릿지가있는 일반적인 솔루션을 모두 해결합니다. ‘Solutio problematis ad geometriam situs pertinentis’라고 불리는이 논문은 나중에 1741 년에 출판되었습니다. 오일러의 논문은 21 개의 번호가 매겨진 단락으로 나뉘며,그 다음에 오일러의 단락의 단순화 된 버전이 제시 될 것입니다.

오일러의 증명의 처음 두 단락에서,그는 Konigsberg 다리 문제를 소개합니다. 제 1 항에서,오일러한다는 것을 믿고 이 문제가 기하학이지만,형상 잘 알려진 그의 동시대에 의해,관련 측정 및 계산이지만,대신 새로운 종류의 형상하는 라이프니츠 라고 형상의 위치입니다. 그런 다음 2 단락에서 오일러는 청중에게 Konigsberg 문제가 어떻게 작동하는지 설명합니다. 오일러 제공의 스케치 문제(볼 오일러의 그림 1),그리고 일곱 뚜렷한 교량:a,b,c,d,e,f 및 g. 이 단락에서 그는 미국의 일반적인 질문의”하나는 알 수하는지 여부 가능한 십자가 각 브리지 정확히 한 번?”

오일러의 그림 1 에서’솔루션 problematis 광고 geometriam 세도 pertinentis,’Eneström53

알리는 일반적인 질문에 그 해결하려는,오일러를 시작 탐구하는 다른 방법을 찾는 솔루션입니다. 제 3 항에서,오일러는 독자를 알려주는 이를 해결하기 위해 특정 문제,그는 쓸 수 있는 아래로 가능한 모든 경로,하지만 이 기술을 것을 많은 시간,작동하지 않을 것입을 위한 큰 구성으로 더 많은 교량과 땅 질량. 이러한 문제 때문에 오일러는이 문제를 해결하기위한 다른 방법을 선택하기로 결정했습니다.

4 단락에서 그는 다리의 교차점을 나타내는 편리한 시스템을 발명함으로써 문제를 단순화하기 시작합니다. 오일러는 다리의 교차점을 나타내는 소문자를 사용하는 대신 landmasses 를 나타내는 대문자를 쓸 것이라고 결정합니다. 예를 들어,참조는 그의 그림 1,AB 것을 의미하는 여행을 시작에서 대륙과에 종료 B. 또한,면 여행 한 후에서 대륙 B,누군가가 이동하기로 결정하는 대륙 D,단순히 표시,ABD. 5 단락에서 오일러는 ABDC 에서 4 개의 대문자가 있지만 3 개의 다리 만 교차했다고 설명하는이 과정에 대한 논의를 계속합니다. 오일러는 얼마나 많은 다리가 있더라도 필요한 교차점을 나타내는 문자가 하나 더있을 것이라고 설명합니다. 이 때문에,전 쾨니히 스 베르크 교량 문제에 필요한 다리를 교차하고 따라서 여덟다.

단락 6 에서 오일러는 자신의 방법에 대한 세부 사항을 계속 설명합니다. 그는 독자를 알려주는 경우가 있는 하나 이상의 다리할 수 있는 교차하면서 하나의 대륙,다른 그것이 문제가되지 않는 다리가 사용됩니다. 예를 들어,a 에서 b 까지 여행자를 데려 갈 수있는 두 개의 다리 인 a 와 b 가 있더라도 어떤 다리를 가져갈 지 오일러의 표기법에는 중요하지 않습니다. 이 단락에서 오일러는 자신이 다루고있는 특정 문제에 대해서도 논의합니다. 그는 설명을 사용하여,그 원래 그림,는 쾨니히 스 베르크가 필요한 문제점을 정확히 여덟 편지는 쌍(A,B)및(A,C)나타나야 합니다 다른 정확히,두 번에 상관없이 문자가 먼저 나타납니다. 또한,쌍(A,D),(B,D)및(C,D)발생해야 합니다 함께 정확히 한 번에 대한 경로는 십자가 각각 다리를 한 번만이 존재하고 있습니다.

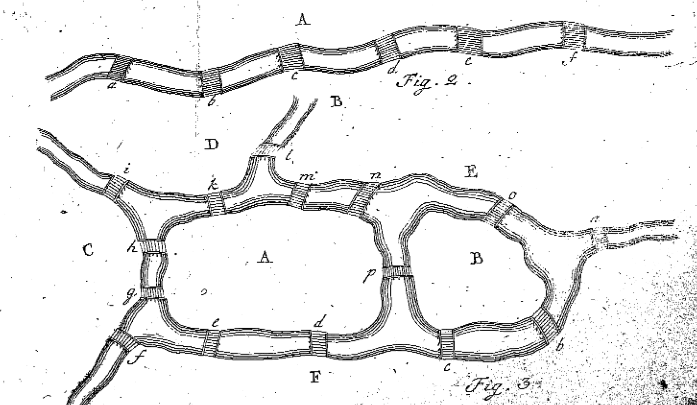
오일러의 2 및 도 3 에서’솔루션 problematis 광고 geometriam 세도 pertinentis,’Eneström53

In Paragraph7,오일러 알려는 독자는 그를 찾을 필요가 있는 여덟-letter 시퀀스를 만족하는 문제,또는 그를 증명할 필요가 없다는 것 같은 시퀀스가 존재합니다. 는 것이 불가능할지도 모르기 때문이 이에 대한 쾨니히 스 베르크 브리지 문제,그 결정을 찾는 규칙을 발견하는 경로가 존재에 대한 일반적인 문제입니다. 그는 landmasses 와 bridges 의 훨씬 간단한 예를 보면서 단락 8 에서이 작업을 수행합니다. 오일러는 그림 2 를 그리며 지역 A 가 통과하는 상황을 평가하기 시작합니다. 오일러(Euler)는 bridge a 가 한 번 여행 한 경우 a 가 여행이 시작되거나 끝난 곳이므로 한 번만 사용되었다고 말합니다. 교량 a,b 및 c 가 모두 한 번 여행 한 경우 a 는 시작 또는 종료 장소 일지라도 정확히 두 번 사용됩니다. 마찬가지로,5 개의 교량이 A 로 이어질 경우,landmass A 는 여행에서 정확히 3 번 발생합니다. 오일러(Euler)는”일반적으로 브리지 수가 홀수 인 경우 1 씩 증가하면 a 의 발생 수는 결과의 절반입니다.”다시 말해서,있는 경우에는 홀수의 다리를 연결하는 다른 대륙에 추가 하나의 수리,그리고 나눌에 의해 두는 방법을 찾아 많은 총 회에서 사용해야 하는 경로,각 다리가 사용되는 한 번만(i.e A 의 총 발생은 홀수#의 다리=(#의 다리-1)/2).

이 사실을 사용하여 Euler 는 9 단락의 Königsberg bridge 문제를 해결합니다. 이 경우,a 로 이어지는 다섯 개의 다리가 있기 때문에 세 번 발생해야합니다(위의 그의 그림 1 참조). 마찬가지로,B,C 및 D 는 모두 그들로 이어지는 세 개의 다리를 가지고 있기 때문에 두 번 나타나야합니다. 따라서 3(a 의 경우)+2(B 의 경우)+2(C 의 경우)+2(D 의 경우)=9 이지만 오일러는 이미 7 개의 브리지에 대해 8 개의 발생 만 있어야한다고 말했습니다. 이것은 모순입니다! 따라서 쾨니히 스 베르그(Königsberg)시의 다리를 한 번만 여행하는 것은 불가능합니다. 끝인가,아니면? Königsberg 의 사람들은이 솔루션에 만족할 수 있지만 위대한 수학자 Leonhard Euler 는 만족하지 못했습니다. 오일러는보다 일반적인 상황을 다루기 위해 그의 증거를 더 계속합니다.

오일러의 일반화

단락 10,오일러 그의 토론을 계속해서 주목할 경우 상황을 포함한 모든 대륙의 홀수 교량,을 말하는 것이 가능 여부를 여행을 사용하여 만들 수 있습니다 각 브리지습니다. 오일러는 각 글자가 나타나야하는 횟수의 합이 하나 더 있으면 총 다리 수,여행을 할 수 있다고 말합니다. 그러나 발생 횟수가 다리 수보다 1 회 이상 많으면 쾨니히 스 버그 다리 문제와 같이 여행을 할 수 없습니다. 이 때문에 규칙,오일러 제공하는 홀수의 다리를 사용하여,그의 그림 2,사실에 대한 일반적인 상황에 있는지 여부에만 다른 하나의 대륙이나 하나 이상의.

단락 11 과 12 에서 오일러는 지역에 짝수 개의 다리가 붙어있는 상황을 다룹니다. 이 상황은 Königsberg 문제에 나타나지 않으므로 지금까지 무시되었습니다. 짝수 브릿지가있는 landmass X 가있는 상황에서 두 가지 경우가 발생할 수 있습니다. 첫 번째 경우는 X 가 여행의 출발점 인 경우입니다. 이 경우 X 는 한 번 시작점으로,다시 종료점으로 두 번 나타납니다. 다른 경우에는 X 가 시작점이 아닙니다. 이 일이 있었다,X 만 나타나 한 번,여행 등을 통해 입력 중 하나교하고 즉시 떠나를 통해서만 다른 하나의 가능합니다. 마찬가지로 X 에 연결된 4 개의 브리지가있는 경우 X 의 발생 횟수는 시작점인지 여부에 따라 다릅니다. 여행이 X 에서 시작되면 세 번 나타나야하지만 X 에서 시작되지 않으면 두 번만 나타납니다. 그래서 일반적으로,경우에는 짝수 교량의 첨부된 다음 경우,여행은 시작하지 않 X,X 가 나타납 반 횟수 교량으로(즉 X 가 짝수이고 시작점이 아닌 x 의 발생=(교량의#)/2). 여행이 X 에서 시작되면 X 는 교량으로 절반의 횟수를 더한 것으로 나타납니다(즉,X 가 짝수이고 시작점=((교량의#)/2)+1 인 X 의 발생).

단락에서는 13 15,오일러는 설명하는 방법을 파악하는 경우 사용하여 경로를 각각 다리를 한 번만이 존재하고 제 자신의 예는 어떻게 작동하는지 보여주는. 오일러 먼저 설명한 그의 간단한 단계 방법을 해결하는 모든 일반적인 상황과 구분 대륙에 의해 강로 연결되는 다리가 있습니다. 첫 번째 오일러는 각 토지를 나타냅니다.대문자가있는 매스. 두 번째로 그는 총 교량 수를 취하고 하나를 추가하고 그가 만들려고하는 차트 위에 이것을 씁니다. 다음으로,그는 대문자를 가져 와서 칼럼에 넣고 그 옆에 다리 수를 씁니다. 넷째,그는 짝수 개의 다리가있는 지평을 별표로 나타냅니다. 그런 다음 각 짝수 옆에 숫자의 ½을 쓰고 각 홀수 옆에 ½을 더한 숫자를 배치합니다. 마지막으로,오일러에 추가 작성된 번호에서 바로 열리는 경우가보다 하나,또는 동등수 교량의 플러스 중 하나,그런 다음 필요한 여행이 가능합니다. 하는 것이 중요하고 그러나,경우에는 합계가 하나의 숫자 이상의 플러스 다리,다음 여행에서 시작해야 하나의 대륙 별표로 표시. 합계가 다리 수를 더한 것과 같으면 별표가 표시되지 않은 지역에서 여행을 시작해야합니다.

예제

Konigsberg 문제를 그의 첫 번째 예 Euler 로 사용하는 것은 다음을 보여줍니다:

수 교량=7,수 교량의 플러스 하=8

지역리 시간 지역이 나타나야 합니다.

5 3

B3 2

C3 2

3 2

나, 3 + 2 + 2 + 2 = 9, 는 8 개 이상, 그래서 여행은 불가능합니다.

이 예 아니라 기본,오일러 결정을 디자인하는 자신의 상황으로 두 섬,네 개의 강,그리고 십습니다. 오일러가 만든 상황은 위의 그림 3 에서 볼 수 있습니다. 오일러는 이제 누군가가 각 다리를 한 번만 지나갈 수있는 경로가 있는지 여부를 알아 내려고합니다. 오일러는 다음과 같은 단계를 위와 같이,이름 지정 다섯 가지 서로 다른 지역 자본 문자,테이블을 만들고 그것을 확인 가능한 경우에,다음과 같다.

수 교량=15, 숫자의 다리 플러스의 하나=16

지역리 시간 지역이 나타나야 합니다.

A*8 4

B*4 2

C*4 2

3 2

E5 3

F*6 3

에, 4 + 2 + 2 + 2 + 3 + 3 = 16, 는 같은 수의 다리,플러스,하나는 것을 의미하는 여행은,사실이 가능합니다. 합계는 교량의 수를 더한 것과 같기 때문에 여행은 D 또는 E 에서 시작해야합니다. 이제 오일러가 여행을 할 수 있다는 것을 알았으므로 그가해야 할 일은 경로가 어떻게 될지 명시하는 것입니다. 오일러는 경로 EaFbBcFdAeFfCgAhCiDkAmEnApBoElD 을 선택,여기서 그는 다리가 landmasses 을 나타내는 문자 사이에 교차되는 포함. 이 정보는 관계없는 반면,정확한 다리는 여행이 가능하다는 것을 아는 데 중요하지 않으므로 경로를 선택할 때 유용합니다. 이것은 오일러가 이러한 성질의 문제를 해결할 때 사용할 방법을 보여주는 좋은 예입니다.

오일러의 결론

다음 몇 가지 단락에서,오일러 제공하는 또 다른 방법을 파악하는 경우 여행이 만들 수 있습니다 어떤 설정의 공포 영화,교량과 강이 있습니다. 16 단락에서 오일러는 육지 오른쪽에 직접 나열된 숫자의 합계가 총 교량 수의 두 배까지 더해진다는 점을 지적합니다. 이 사실은 나중에 핸드 쉐이킹 렘마로 알려지게됩니다. 기본적으로 핸드 쉐이킹 렘마(handshaking lemma)는 각 다리가 부착 된 각 landmass 에 대해 한 번 두 번 계산된다고 말합니다. 17 단락에서 오일러는이 숫자의 절반이 총 교량 수와 같기 때문에 각 지역으로 이어지는 모든 교량의 합이 짝수임을 명시합니다. 그러나 홀수의 브릿지가있는 홀수의 육지가있는 경우에는 불가능합니다. 따라서 오일러는 토지 질량에 몇 가지 홀수가 붙어있는 경우 이러한 육지의 짝수가 있어야한다는 것을 증명합니다.

그러나,이것은 충분하지 않을 증명하는 경우가 있는 경로를 각각 다이 한 번 사용되며,한 번만으로는 쾨니히 스 베르크리제도의 수는 대륙의 홀수리가 그들을. 이 때문에 오일러는 단락 18 과 19 에 더 많은 제한을 추가합니다. 오일러는 이후의 총 숫자의 다리에 부착하여 각 대륙과 같은 두 번의 수는 다리(에서 볼 수 있듯이 핸드셰이킹 lemma),그래서 그러므로 추가할 경우 두 가지 이에 합한 다음 나누는 두 가지에 의해,당신의 수를 얻을 것이다 총리 플러스의 하나입니다. 이 숫자는 이전에 사용 된 것과 동일하며 경로가 가능한지 알려주는 데 사용됩니다. 모든 숫자가 짝수 인 경우 테이블의 세 번째 열은 총 브리지 수를 더한 것보다 작은 하나에 합산됩니다.

오일러 그는 그것은 분명이 있는 경우 두 대륙의 홀수 교 여행이 항상 가능한 경우에 여행은 시작에 하나의 영역 홀수의 다리가 있습니다. 이 때문입니다 경우에도 숫자가 절반으로,그리고 각각의 이상한 사람이 하나씩 증가하고 절반으로 합계는 이들의 반쪽이 동일한 하나 더 많은 다음의 총수는 다리가 있습니다. 그러나 홀수의 교량을 가진 4 개 이상의 육지가있는 경우 경로가있는 것은 불가능합니다. 이 때문에의 합의 절반 이상한 숫자 중 하나와 함께 그 모든 합의 절반의 짝을 만들 것입 sum 세 번째 열의보다 큰 교량의 총 수 plus 하나입니다. 따라서 오일러는 단지 홀수 개의 다리를 가진 대부분의 두 개의 지대가있을 수 있음을 증명했습니다.

이 언급되고,오일러는 이제 그의 결론에 관한 일반적인 형태의 쾨니히 스 베르크리 문제입니다. 항 20,오일러 제공하는 세 가지 지침이 있는 누군가 사용할 수 있는 그 밖으로 경로의 존재를 사용하여 각각 다리를 한 번만. 첫째,그는 홀수 개의 다리가있는 2 개 이상의 육지가 있다면 그러한 여정이 불가능하다고 주장했다. 둘째,경우의 수리 홀수 위해 정확히 두 개의 대륙,그 여행은 가능한 경우에 시작 하나 홀수 landmasses. 마지막으로 오일러는 홀수의 육지가있는 지역이없는 경우 모든 지역에서 시작하여 여행을 수행 할 수 있다고 말합니다. 후에는 이러한 세 가지 사실,오일러 그 결 증거와 함께 21 조,단순히국 후에는 수치하는 경로가 존재하는지,그들은 여전히 통과해야 하는 노력을 작성하는 경로를 작동합니다. 오일러는 이것을 성취하는 방법이 사소한 것이라고 믿었으며,그것에 많은 시간을 할애하고 싶지 않았습니다. 그러나,오일러았는 제안에 집중하는 방법에서 하나의 대륙을 다른,에 집중하는 대신 특정교합니다.

오일러의 증거하고 그래프 이론

읽을 때 오일러의 원 증거는 비교적 간단하고 쉽게 이해할 수 있는 작업의 수학;그러나,그것은 실제적인 증거 하지만 중간 단계는 이 문제는 유명합니다. 오일러의 혁신에 있었기에 쾨니히 스 베르크리 문제를 추상적으로 사용하여 라인과 문자를 나타내는 더 큰 상황의 공포 영화이다. 그는 landmasses 를 표현하기 위해 대문자를 사용하고 다리를 표현하기 위해 소문자를 사용했습니다. 이것은 완전히 새로운 형식의 사고를 위한 시간,그리고 그의 종이,오일러로 촉발의 새로운 지점을 수학이라는 그래프 이론,그래프는 것은 단순히 컬렉션의 꼭지점과 가장자리입니다. 오늘날 그래프의 각 가장자리를 한 번만 포함하고 한 번만 포함하는 그래프의 경로를 이 문제 때문에 오일러 리안 경로라고합니다. 시간에서 오일러는 이 문제를 해결하는 오늘날,그래프론 중요한 수학의 지점,사는 것의 기준이 우리의 생각에 대한 네트워크입니다.

쾨니히 스 베르크 브리지 문제는 이유는 빅스 states,

기원의 그래프 이론는 겸손하게도,경솔…는 문제의 개발을 주도하는 그래프 이론은 종종 조금 더 이상 퍼즐을 테스트하도록 설계된 독창성이 아닌 상상력을 자극하. 그러나에도 불구하고 명백한 사소한의 이러한 퍼즐,그들은 점령자의 수학자,결과 함께는 그래프 이론가 피사체에서 풍부한 이론적 결과의 놀라운 다양하고 깊이가 있습니다.

으로 빅스의 성명이 암시하듯이,이 문제는 그것을 언급한 첫 번째 장에서의 그래프 이론의 책을 정독 도서관에서 사용할 수 있습니다.

후 오일러의 검색(또는 본 발명에 따라,어떻게 독자를 살펴 봅니다),그래프 이론 붐과 함께 중요한 기여해 만든 훌륭한 수학자들은 어거스틴 코시,윌리엄 해밀턴,아서 케일,구스타프 Kirchhoff,조지 Polya. 이러한 남자의 모든 기여 폭로”모든 것에 대해 잘 알려져 있지만 주문하는 그래프 등의 격자에 의해 형성 원자에서 결정 또는 육각형 격자에 의해 만들어에 꿀벌는 곳이다.”다른 유명한 그래프 이론의 문제를 포함하는 방법을 찾는 미로에서 탈출 또는 미로,또는 이동 순서와 기사에 체스판을 각각 착륙에서 한 번만 기사에 반환하는 공간에서 그가 시작되었습니다. 몇 가지 다른 그래프 이론 문제는 수세기 동안 풀리지 않았습니다.

의 운명 Konigsberg

는 동안 그래프 이론 붐 후 오일러는 해결 쾨니히 스 베르크 브리지,문제의 마을에 쾨니히 스 베르크가 있었는 훨씬 다른 운명이다. 1875 년 Königsberg 의 사람들은 노드 B 와 C 사이에 새로운 다리를 건설하기로 결정하여이 두 landmasses 의 링크 수를 4 개로 늘 렸습니다. 이 의미는 두 대륙했는 홀수의 링크 주소 간단한 솔루션을하는 문제입니다. 창조의 다리가 있거나 없을 수 있었다 무의식적으로 발생하는 욕망에 의해 경로를 해결하는 도시의 유명한 문제입니다.

그러나,새로운 다리하지 않았를 해결하는 모든 쾨니히 스 베르크의 미래의 문제를,마지 않았다는 기대에 다시기를”슬픔과 전쟁의 운명을 기다리고 그것으로 호스트에 대한 한의 치열한 전투 중 하나입니다.”1944 년 8 월 4 일 동안 영국 폭격기는 구시 가지와 쾨니히 스 베르크의 북부 지역을 모두 파괴했습니다. 1945 년 1 월과 2 월에 쾨니히 스 베르크를 둘러싼 지역은 러시아 군에 둘러싸여 있습니다. 독일 민간인은 마을에서 대피하기 시작하지만 너무 늦게 움직입니다. 쿠로 니안 라군의 얼음이 많은 물 건너 보트와 도보로 도망치려 고 수천 명의 사람들이 사망합니다. 1945 년 4 월,붉은 군대는 구시 가지의 약 90%가 폐허에 누워있는 쾨니히 스 베르크를 점령합니다.

Königsberg 의 현재 거리지도가 아래에 제공됩니다. 이지도는 마을이 얼마나 바뀌 었는지 보여줍니다. 많은 교량 파괴되었 동안 폭격,그리고 마을 할 수 있는 더 이상 요청이 같은 흥미로운 질문들에됩니다. 크게 다른 레이아웃과 함께 Königsberg 마을에는 Pregel 강이 Pregolya 로 개명 된 칼리닌그라드라는 새로운 이름이 있습니다. 동의 운명에 쾨니히 스 베르크로 끔찍한,시민 오래된 커피의 문제에 통과하는 각의 오래된 세븐 브리지 정확하게 한 시간 주도 형성의 완전히 새로운 수학의 지점,그래프 이론이다.나는 이것이 내가 할 수있는 유일한 방법이라고 생각한다. 그래프 이론:1736-1936. 옥스포드:클라렌던 프레스,1976.

던햄,윌리엄. 오일러:우리 모두의 주인. 워싱턴: 미국의 수학 협회,1999.

오일러,Leonhard,’Solutio problematis ad geometriam situs pertinentis'(1741),Eneström53,MAA 오일러 아카이브.

“수학의 역사:Leonhard Euler 에(1707-1783).”ScienceWeek(2003). 6 11 월. 2005.

홉킨스,브라이언,로빈 윌슨. “쾨니히 스 베르크에 대한 진실.”대학 수학 저널(2004),35,198-207.

“Konigsberg 교량.”Mactutor History Of Mathematics Archive:
http://www-history.mcs.st-and.ac.uk/history/Miscellaneous/other_links/Konigsberg.html

편집자 주: 이 기사는 원래 Convergence,Volume3(2006)에 게시되었습니다.