Editor’S Note

次の学生研究レポートは、ニュージャージー大学で開催されたJudit Kardos教授のMath255クラスのために作成されました。 これは数学の歴史の中で3単位の入門コースでした。 このレポートは最終的な等級の30%の方に数えられました。 これは、学生が二次的な情報源を使用して行うことができるような歴史的研究の一例です。

レナード-オイラーのケーニヒスベルク橋の問題に対する解決策

ケーニヒスベルク

私たちの物語は、プレゲル川のほとりにあるプロイセンのケーニヒスベルクの趣のある町で、18世紀に始まります。 1254年、ドイツ騎士団はプロイセンに対する第二次十字軍の後、ボヘミア王オットー2世の指導の下、ケーニヒスベルク市を設立した。 中世には、ケーニヒスベルクは非常に重要な都市と貿易の中心地となり、その場所は戦略的に川に位置していました。 18世紀の作品は、ケーニヒスベルクを繁栄した都市として示しています,船の艦隊はPregelを埋める場所,そして彼らの貿易は、地元の商人とその家族の両方に快適なライフスタイルを提供しています. 健全な経済は、都市の人々が川を渡って7つの橋を建設することを可能にし、そのほとんどはクナイホフ島に接続していました。

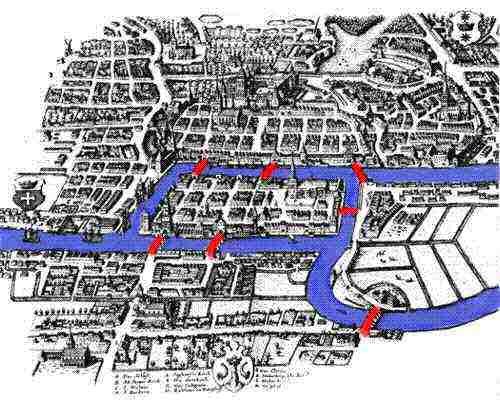
川がクナイフォフの周りを流れ、文字通りパブヤードと別の島を意味するように、それは四つの異なる地域に都市を分 七つの橋は鍛冶橋、接続橋、緑の橋、商人の橋、木製の橋、高い橋、蜂蜜の橋と呼ばれていました。 伝承によると、ケーニヒスベルクの市民は日曜日の午後に美しい街を歩いて過ごしていました。 歩いている間、街の人々は自分たちのためにゲームを作ることにしました。 ケーニヒスベルクの市民の誰も一度だけそれぞれの橋を渡ることを可能にするルートを発明することはできませんでしたが、それでも彼らはそれが不可能であることを証明することはできませんでした。 彼らにとって幸運なことに、ケーニヒスベルクは有名な数学者Leonard Eulerの故郷であるサンクトペテルブルクからそれほど遠くはありませんでした。 なぜオイラーは数学の分野とは無関係な問題に自分自身を懸念するのでしょうか？

なぜそのような偉大な数学者は、ケーニヒスベルク橋の問題のような些細な問題で多くの時間を費やすのでしょうか？ オイラーは明らかに忙しい人で、生涯に500冊以上の本や論文を出版していました。 1775年だけで、彼は週に1つの数学的な論文の平均を書いて、彼の生涯の間に彼は力学、光学、天文学、ナビゲーション、流体力学などの数学以外の様々なトピッ オイラーがこの問題が些細なことだと感じたことは驚くべきことではなく、1736年にダンツィヒ市長のCarl Leonhard Gottlieb Ehlerに宛てた手紙の中で、彼は問題の解決策を求めました。

。 . . したがって、あなたは、最も高貴な先生を参照してください、どのようにこのタイプのソリューションは、数学との関係がほとんどない、と私はあなたが数学者がそれを生成することを期待する理由を理解していない、むしろ他の誰よりも、解決策は、単独の理由に基づいており、その発見は、任意の数学的原理に依存していません。 このため、数学との関係がほとんどない質問でさえ、なぜ数学者によって他の人よりも早く解決されるのか分かりません。

オイラーは問題が些細であることを発見したにもかかわらず、彼はまだそれに興味をそそられました。 同じ年にイタリアの数学者でエンジニアであるGiovanni Marinoniに書かれた手紙の中で、オイラーは言った、

この質問はとても平凡ですが、私には幾何学、代数、計数の芸術さえもそれを解決するのに十分であったことに注目する価値があるように見えました。

オイラーは、この問題は、Gottfried Wilhelm Leibnizがかつて議論し、ライプニッツがgeometria situs、または位置の幾何学と呼ばれるものであると考えていました。 このいわゆる位置の幾何学は、現在グラフ理論と呼ばれるものであり、オイラーはこの有名な問題を解決しながら導入し、利用しています。

オイラーの証明

1735年8月26日、オイラーはKonigsberg bridge問題の解を含む論文を提示します。 彼はこの特定の問題と、任意の数の陸橋と任意の数の橋の一般的な解決策の両方に対処しています。 この論文は”Solutio problematis ad geometriam situs pertinentis”と呼ばれ、後に1741年に出版された。 オイラーの論文は二十から一段落に分かれており、以下では、オイラーの段落の簡略化されたバージョンが提示されます。オイラーの証明の最初の2つの段落では、彼はKonigsberg Bridge問題を紹介します。 パラグラフ1では、オイラーは、この問題は幾何学に関係していると考えているが、測定と計算を含む同時代の人々によってよく知られている幾何学ではなく、ライプニッツが位置の幾何学と呼んだ新しい種類の幾何学であると考えていると述べている。 その後、パラグラフ2で、オイラーはKonigsberg問題がどのように機能するかを聴衆に説明します。 オイラーは問題のスケッチを提供し（オイラーの図1を参照）、a、b、c、d、e、f、および、gの七つの異なる橋と呼ばれています。”

オイラーの図1’Solutio problematis ad geometriam situs pertinentis,’Eneström53

彼が解決しようとしている一般的な質問を述べた後、オイラーは解を見つけるさまざまな方法を探 パラグラフ3では、オイラーは、この特定の問題を解決するために、彼はすべての可能なパスを書き留めることができることを読者に伝えますが、この技 これらの問題のために、オイラーはこの問題を解決するための別の方法を選択することに決めました。

パラグラフ4では、彼は橋の交差を表現するための便利なシステムを発明することによって問題を簡素化し始めます。 オイラーは、橋の交差を表すために小文字を使用する代わりに、陸地を表す大文字を書くと判断しました。 例えば、彼の図1を参照すると、ABはlandmass Aからbに移動した後、誰かがlandmass Dに移動することを決定した場合、これは単にABDと表示されます。 パラグラフ5では、オイラーはABDCでは4つの大文字があるが、3つの橋しか交差していないことを説明するこのプロセスについての議論を続けている。 オイラーは、いくつの橋があっても、必要な交差点を表すためにもう一つの文字があると説明しています。 このため、ケーニヒスベルク橋の問題の全体では、7つの橋を渡る必要があり、したがって8つの大文字が必要でした。

パラグラフ6では、オイラーは彼の方法の詳細を説明し続けています。 彼は、ある陸塊から別の陸塊に行くときに渡ることができる複数の橋がある場合、どの橋が使用されているかは問題ではないと読者に言います。 たとえば、aからBへの旅行者を取ることができる2つの橋、aとbがあるとしても、どの橋が取られるかはオイラーの表記法では問題ではありません。 この段落では、オイラーはまた、彼が扱っている特定の問題について説明します。 彼は、元の図を使って、ケーニヒスベルク問題には正確に8文字が必要であり、（A、B）と（A、C）のペアは、どの文字が最初に現れても、正確に2回隣り合って現れなけ さらに、(A,D)、(B,D)、および(C,D)のペアは、各ブリッジを1回だけ通過するパスが存在するためには、正確に1回一緒に発生する必要があります。

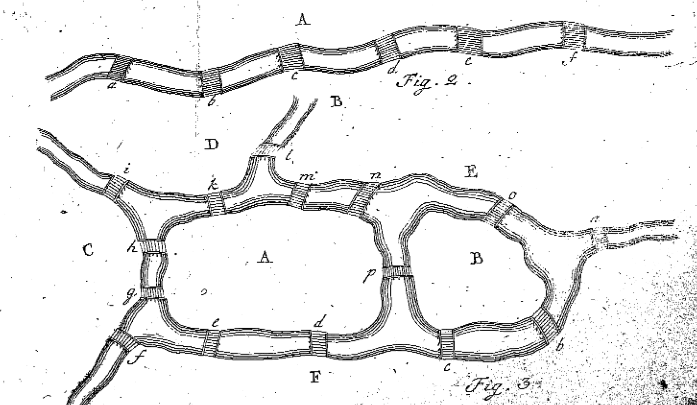
オイラーの図2と3’Solutio problematis ad geometriam situs pertinentis,’Eneström53

パラグラフ7では、オイラーは問題を満たす八文字のシーケンスを見つける必要があるか、そのようなシーケンスが存在しないことを証明する必要があることを読者に知らせる。 彼はケーニヒスベルク橋の問題のためにこれを行う前に、彼はより一般的な問題のためのパスが存在するかどうかを発見するためのルールを見つけるこ 彼は、陸橋と橋のはるかに簡単な例を見て、パラグラフ8でこれを行います。 オイラーは図2を描き、領域Aが通過する状況を評価し始めます。 オイラーは、橋aが1回移動された場合、aは旅が始まったか終了した場所であり、したがって1回しか使用されなかったと述べています。 ブリッジa、b、およびcがすべて1回移動された場合、開始場所であるか終了場所であるかに関係なく、Aは正確に2回使用されます。 同様に、5つの橋がAにつながる場合、陸塊Aは旅の中で正確に3回発生します。 オイラーは、「一般に、ブリッジの数が奇数であり、それが1つ増加した場合、aの出現回数は結果の半分になります。”つまり、aを他の陸橋に接続する橋の数が奇数の場合は、橋の数に1を加えて2で除算し、各橋が一度だけ使用されるパスでAを使用する必要があ Aが奇数のブリッジ数=(#Of Bridges-1)/2を持つ場合、Aの合計出現数。

この事実を使用してオイラーは、パラグラフ9のケーニヒスベルク橋の問題を解決します。 その場合、Aにつながる5つのブリッジがあるので、3回発生する必要があります（上の図1を参照）。 同様に、B、C、およびDは、それらにつながる3つのブリッジをすべて持っているため、2回表示する必要があります。 したがって、3（A）+2（B）+2（C）+2（D）=9ですが、オイラーはすでに7つの橋には8つの出現しかないと述べています。 これは矛盾です！ したがって、ケーニヒスベルク市の橋を一度だけ旅行することは不可能です。 終わりか、それともそれですか？ ケーニヒスベルクの人々はこの解に満足しているかもしれませんが、偉大な数学者Leonhard Eulerは満足していませんでした。 オイラーはさらに、より一般的な状況に対処するための彼の証明を続けています。

オイラーの一般化

パラグラフ10では、オイラーは、状況が奇数の橋を持つすべての陸橋を含む場合、各橋を一度だけ使用して旅を行うことがで オイラーは、各文字が表示されなければならない回数の合計がブリッジの合計数よりも多い場合、旅をすることができると述べています。 しかし、発生回数が橋の数よりも多い場合、ケーニヒスベルク橋の問題のように、旅をすることはできません。 これは、オイラーが彼の図2を使って奇数の橋に対して与える規則が、他の陸地が1つだけであるか、複数であるかにかかわらず、一般的な状況に当てはまるからである。

パラグラフ11と12では、オイラーは、領域に偶数のブリッジが接続されている状況を扱っています。 このような状況はケーニヒスベルク問題には現れないため、今まで無視されてきました。 橋の数が偶数の陸塊Xの状況では、二つのケースが発生する可能性があります。 最初のケースは、Xが旅の出発点である場合です。 この場合、Xは2回、開始点として1回、終了点として再び表示されます。 他の場合、Xは出発点ではありません。 これが起こった場合、旅は一つの橋を通って入力し、すぐに利用可能な唯一の他のものを通過しなければならないので、Xは一度だけ表示されます。 同様に、xに4つのブリッジが接続されている場合、Xの出現回数は、それが開始点であるかどうかによって異なります。 旅がXで始まる場合、それは3回現れなければなりません、しかしそれがXで始まらなければ、それは2回しか現れません。 したがって、一般に、Xに偶数のブリッジが接続されている場合、旅がXで開始されない場合、Xはブリッジとしての回数の半分に表示されます（すなわ Xが偶数であり、開始点ではないxの出現=(ブリッジの数)/2)。 旅がXで始まる場合、Xは橋としての回数の半分に1を加えたものになります（つまり、Xが偶数で開始点=((橋の数)/2)+1)。

パラグラフ13から15では、オイラーは、各ブリッジを一度だけ使用するパスが存在するかどうかを把握する方法を説明し、それがどのように動作す オイラーは最初に、河川で分割され、橋で接続された陸塊を持つ一般的な状況を解決するための彼の簡単な六段階の方法を説明します。 最初のオイラーは、大文字で各陸塊を示します。 第二に、彼は橋の総数を取り、一つを追加し、彼が作ろうとしているチャートの上にこれを書いています。 次に、彼は大文字をとり、それらを列に入れ、その隣に橋の数を書きます。 第四に、彼はアスタリスクで偶数の橋を持つ陸塊を示します。 次に、各偶数の隣に、彼は数の½を書き込み、各奇数の隣に彼は½に数を加えたものを置きます。 最後に、オイラーは右端の列に書かれた数字を加算し、合計がブリッジの数に1を加えたものよりも小さいか等しい場合、必要な旅が可能です。 ただし、合計が橋の数に1を加えたものよりも1少ない場合、旅はアスタリスクでマークされた陸地の1つから開始する必要があることに注意するこ 合計が橋の数に1を加えた数に等しい場合、旅はアスタリスクでマークされていない地域で開始する必要があります。

例

彼の最初の例オイラーとしてKonigsberg問題を使用して、次のことを示しています:

ブリッジの数=7、ブリッジの数プラス1=8

リージョンブリッジ時間領域が表示されなければなりません

A5 3

B3 2

C3 2

D3 2

, 3 + 2 + 2 + 2 = 9, これは8以上なので、旅は不可能です。

この例はかなり基本的なものなので、オイラーは二つの島、四つの川、十五の橋で自分の状況を設計することに決めました。 オイラーが作成した状況は、上の彼の図3に見ることができます。 オイラーは今、誰かが一度だけ各橋を渡ることを可能にするパスがあるかどうかを把握しようとします。 オイラーは、上記と同じ手順に従って、大文字で五つの異なる領域を命名し、次のように、可能であればそれをチェックするためのテーブルを作成します。

ブリッジの数=15、ブリッジの数プラスワン=16

リージョンブリッジ時間領域が表示されなければなりません

A*8 4

B*4 2

C*4 2

D3 2

E5 3

f*6 3

さらに, 4 + 2 + 2 + 2 + 3 + 3 = 16, これは橋の数に1を加えたものですこれは実際には旅が可能であることを意味します。 合計はブリッジの数に1を加えたものに等しいので、旅はDまたはEのいずれかで開始する必要があります。 オイラーが旅をすることが可能であることを知ったので、彼がする必要があるのは、道がどうなるかを述べることだけです。 オイラーは、パスE A F B B C F D A E F F C Gahcidkamenapboeldを選択します,彼は陸塊を表す文字の間に交差している橋が含まれています. この情報は無関係ですが、正確な橋は旅が可能であることを知る上で重要ではないので、パスを選択するときに役立ちます。 これは、オイラーがこの性質の問題を解決するときに使用する方法を示す良い例です。

オイラーの結論

次のいくつかの段落では、オイラーは、陸橋、橋、川の任意のセットを与えられた旅を行うことができるかどうかを把握す パラグラフ16では、オイラーは、陸地の右に直接記載されている数字の合計が橋の総数の2倍になることを指摘しています。 この事実は後にhandshaking lemmaとして知られるようになります。 基本的に、ハンドシェイク補題は、各橋が接続されている各陸塊について、各橋が2回、1回カウントされると述べています。 パラグラフ17では、オイラーは、この数の半分が橋の総数に等しいので、各地域につながるすべての橋の合計は偶数であると述べています。 しかし、奇数個の橋を持つ奇数個の陸塊が存在する場合、これは不可能である。 したがって、オイラーは、陸塊に奇数が付いている場合、これらの陸塊の偶数がなければならないことを証明しています。

しかし、ケーニヒスベルク橋の問題は、それらに行く橋の数が奇数で偶数の陸塊を持っているので、各橋が一度だけ使用される経路がある場合、これは証明するのに十分ではありません。 このため、オイラーはパラグラフ18と19でより多くの制限を追加します。 オイラーは、各陸塊に接続されている橋の数の合計は橋の数の2倍に等しいので（握手補題に見られるように）、したがってこの合計に2を加えて2で割ると、総橋の数に1を加えたものになると説明しています。 この番号は、パスが可能かどうかを判断するために使用される前に使用されたものと同じです。 すべての数値が偶数の場合、表の3番目の列の合計は、ブリッジの合計数に1を加えたものよりも1少ないものになります。

オイラーは、奇数の橋を持つ2つの陸地がある場合、奇数の橋を持つ地域の1つで旅が始まると、旅は常に可能になることは明らかであると説明し これは、偶数が半分になり、奇数のそれぞれが1ずつ増加して半分になると、これらの半分の合計がブリッジの総数よりも1に等しくなるためです。 しかし、橋の数が奇数の4つ以上の陸橋がある場合、そこに道があることは不可能です。 これは、奇数の半分に1を加えた合計と偶数の半分のすべての合計が、3番目の列の合計をブリッジの合計数に1を加えた合計よりも大きくする したがって、オイラーは、奇数の橋を持つ最大2つの陸地が存在することを証明しました。

これが述べられていると、オイラーは現在、ケーニヒスベルク橋問題のより一般的な形に関する彼の結論を下すことができます。 パラグラフ20では、オイラーは、パスが一度だけ各ブリッジを使用して存在するかどうかを把握するために誰かが使用できる三つのガイドラインを 第一に、彼は、奇数の橋を持つ2つ以上の陸地があるならば、そのような旅は不可能であると主張した。 第二に、橋の数が正確に二つの陸塊に対して奇数である場合、それが二つの奇数の陸塊のいずれかで始まる場合、旅は可能である。 最後に、オイラーは、奇数の陸地を持つ地域がない場合、その旅はどの地域からでも達成できると述べています。 これらの3つの事実を述べた後、オイラーは、単に1つのパスが存在することを把握した後、彼らはまだ動作するパスを書き出すための努力を経なければ オイラーは、これを達成するための方法は些細なものだと信じていた、と彼はそれに多くの時間を費やすことを望んでいませんでした。 しかし、オイラーは、最初は特定の橋に集中するのではなく、ある陸塊から別の陸塊に移動する方法に集中することを提案しました。

オイラーの証明とグラフ理論

オイラーの元の証明を読むと、比較的簡単で分かりやすい数学の仕事が見つかります。 オイラーの大きな革新は、地形や橋のより大きな状況を表現するために線と文字を使用することによって、ケーニヒスベルク橋の問題を抽象的に見るこ 彼は陸塊を表すために大文字を使用し、橋を表すために小文字を使用しました。 これは当時の全く新しいタイプの思考であり、彼の論文では、オイラーは誤ってグラフ理論と呼ばれる数学の新しい枝を引き起こしました。 今日では、グラフの各辺を一度だけ含むグラフ内のパスは、この問題のためにオイラーパスと呼ばれています。 オイラーがこの問題を解決してから今日まで、グラフ理論は数学の重要な枝となり、ネットワークについての私たちの思考の基礎を導いています。

ケーニヒスベルク橋の問題は、なぜBiggsの状態であり、

グラフ理論の起源は謙虚で、軽薄でさえあります…グラフ理論の発展につながった問題は、想像力を刺激するのではなく、創意工夫をテストするために設計されたパズル以上のものであったことが多い。 しかし、そのようなパズルの明白な自明性にもかかわらず、彼らは数学者の関心を捉え、グラフ理論は驚くべき多様性と深さの理論的結果に富んだ主題となっているという結果を得た。Biggsの声明が示唆するように、この問題は非常に重要であり、ライブラリで熟読されたすべてのグラフ理論の本の最初の章で言及されています。

オイラーの発見（または発明、読者がそれをどのように見ているかに応じて）の後、グラフ理論はAugustin Cauchy、William Hamilton、Arthur Cayley、Gustav Kirchhoff、George Polyaのような偉大な数学者によって大きな貢献 これらの男性はすべて、結晶中の原子によって形成された格子や蜂の巣の中の蜂によって作られた六角形の格子など、大きくて秩序のあるグラフに”他の有名なグラフ理論の問題は、迷路や迷路から脱出する方法を見つけること、または各正方形が一度だけに上陸し、騎士が彼が始めた空間に戻るようなチェスボード上の騎士との動きの順序を見つけることが含まれます。 他のいくつかのグラフ理論の問題は何世紀にもわたって未解決になっています。オイラーがケーニヒスベルク橋の問題を解決した後、グラフ理論がブームになったが、ケーニヒスベルクの町ははるかに異なる運命を持っていた。 1875年、ケーニヒスベルクの人々は、ノードBとCの間に新しい橋を建設することを決定し、これら二つの陸塊のリンクの数を四つに増やしました。 これは、2つの陸地だけが奇数のリンクを持っていたことを意味し、これは問題にかなり簡単な解決策を与えました。 余分な橋の創造は、町の有名な問題を解決するための道への欲求によって無意識のうちに引き起こされたかもしれないし、そうでないかもしれ

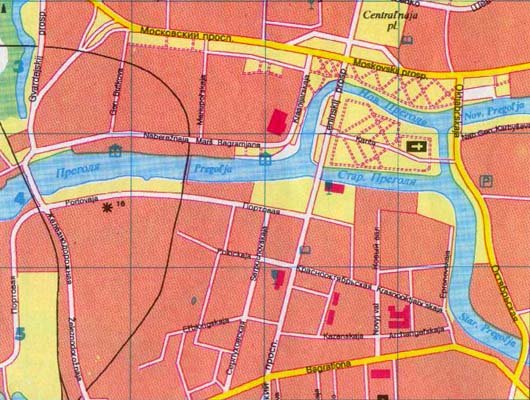
しかし、新しい橋はケーニヒスベルクの将来の問題のすべてを解決するものではありませんでした。「1944年8月の4日間、イギリスの爆撃機は旧市街とケーニヒスベルク北部の両方を破壊しました。 1945年1月から2月にかけて、ケーニヒスベルク周辺地域はロシア軍に包囲された。 ドイツの民間人は町から避難し始めますが、遅すぎる移動します。 何千人もの人々が、クルニアンラグーンの氷の海を渡ってボートと徒歩で逃げようとして殺されています。 1945年4月、赤軍はケーニヒスベルクを占領し、旧市街の約90%が廃墟となった。 Königsbergの現在の通りの地図を以下に示します。

この地図は、町がどのくらい変わったかを示しています。 橋の多くは爆撃の間に破壊され、町はもはや彼らが十八世紀にできたのと同じ興味深い質問をすることはできません。 ケーニヒスベルクの町は、大きく異なるレイアウトに加えて、新しい名前、カリーニングラードを持っており、プレゲル川はプレゴリヤと改名されました。 ケーニヒスベルクの運命は恐ろしいものですが、市民の古いコーヒーハウスの問題は、古い七つの橋のそれぞれを正確に一度横断することによって、数学の全く新しい枝、グラフ理論の形成につながりました。p>

Biggs、Norman L.、E.K.Lloyd、Robin J.Wilson。 グラフ理論：1736-1936。 1976年、クラレンドン・プレス・オクスフォード（英語版）（英語版）。

ダナム、ウィリアム。 オイラー：私たちのすべてのマスター。 ワシントン: アメリカの数学協会、1999。

オイラー,レオンハルト,’Solutio problematis ad geometriam situs pertinentis'(1741),Eneström53,MAA Euler Archive.数学の歴史：レオンハルト-オイラー（1707年-1783年）。”（2003年）に出演した。 年6月号) 2005.

ホプキンス、ブライアン、ロビン-ウィルソン。 “ケーニヒスベルクについての真実。”大学数学ジャーナル（2004）、35、198-207。

“Konigsberg Bridges.”数学アーカイブのMacTutorの歴史：
http://www-history.mcs.st-and.ac.uk/history/Miscellaneous/other_links/Konigsberg.html

編集者のメモ

編集者のメモ: この記事は、もともとConvergence,Volume3(2006)に掲載されました。