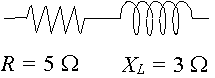9. インピーダンスと位相角
お見逃しなく。..
このページの後半のアプレットで、rlc回路のインピーダンス、電流、電圧を調べます。
インピーダンス
回路のインピーダンスは、回路の要素の組み合わせによる電流の流れに対する総有効抵抗です。/P>
記号:Z
単位: ‘Ω’
すべての3つの要素(抵抗、コンデンサ、インダクタ)の合計電圧が書かれています
VRLC
この合計電圧を見つけるために、電圧VR、VL、VCを追加することはできません。VLとVCは虚数量と見なされるため、次のようになります。
インピーダンスVRLC=IZ
So`Z=R+j(X_L−X_C)`
So’Z=R+j(X_L-X_C)’
ここで、zの大きさ(サイズ、または絶対値)は次のように与えられます:z|=sqrt(R^2+(X_L-X_C)^2`
位相角
`tan\theta=(X_L-X_C)/R`
角度θは、電流と電圧の間の位相角を表します。これをy=a sin(bx+c)のグラフで以前に会った位相角と比較してください。
これをy=a sin(bx+c)のグラフで会った位相角と比較してください。
例1
回路の抵抗は`5\Ω`で、インダクタのリアクタンスは`3\Ω`です。 インピーダンスを複素数で極座標形式で表します。/div>
答え
この場合、
この場合、
したがって、`x_l-x_c=3\ω`となります。
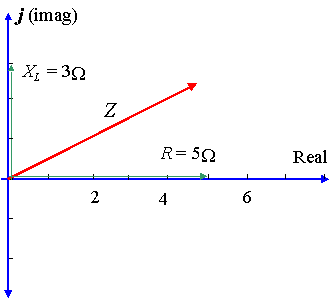
長方形の形では、インピーダンスは次のように書かれています。
`Z=5+3j\Ω`
電卓を使用すると、Zの大きさは`5.83`で与えられ、角度`θ`(位相差)は`30.96^@`で与えられます。
だから、電圧は電流を`30だけリードします。図に示すように、96^@`。
Zを複素数(極座標形式)として表すと、次のようになります。
`Z=5.83≤30.96^@\Ω’。
例2(a)
特定のac回路には、抵抗が`4\Ω`、インダクタ間のリアクタンスが`8\Ω`、コンデンサ間のリアクタンスが`11\Ω`です。 回路のインピーダンスを極座標形式の複素数として表現します。
答え
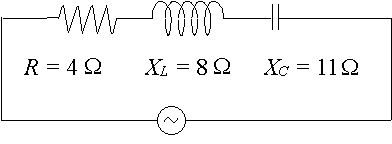
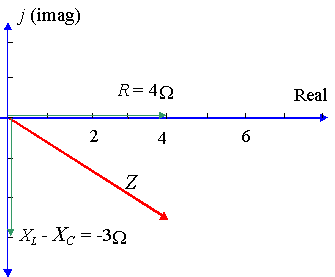
この場合、我々は持っています: `X_L-X_C=8-11=-3\Ω`
だから`z=4-3J\Ω`を長方形の形にします。ここで、極座標形式で表現します。
計算機を使用して、`r=5`と`θ=-36.87^@’を見つけます。P>
だから`Z=5∠-36.87^@\Ω`
インタラクティブなRLCグラフ
以下は、(それは静的な画像ではありません)で再生するイ AC回路の総インピーダンスに及ぼす抵抗、コンデンサ、インダクタの影響を調べることができます。
このインタラクティブのための活動
- まず、ちょうどスライダーで遊びます。 上のスライダを左または右にドラッグして抵抗`R`によるインピーダンスを変化させ、xlスライダを上または下にドラッグしてインダクタ`X_L`によるイ
- XL−XCとZの値に対する異なるインピーダンスの影響を観察します。
- 赤い”結果”線が水平になる角度(ラジアン単位)であるθに対する異なるインピーダンスの影響を観察します。
- インタラクティブで電圧と電流のグラフを考えてみましょう。 スライダーを変更するときに、ラグまたはリードの量を観察します。
- あなたはこのインタラクティブで遊んでから何を学びましたか?