ダーシーの法則は、地質学、特に水文地質学の多くの枝を理解するために重 私たちが法律を見て、それが私たちに伝えることができる前に、それがどのように開発されたかを見てみましょう。 ダーシーの法則は、ディジョンの街の周りに水を供給するために地下加圧パイプシステムを開発した19世紀のフランスの技術者、ヘンリーダーシーにちなんで命名されています。 また、有名なディジョンの噴水に水を提供したシステムは、都市の上下水道システムに革命をもたらしました。 このシステムはポンプを必要とせず、純粋に重力によって駆動されました。 新しいシステムを開発する過程で、Darcyは重力だけを使って水を動かそうとした一連の実験を行った。

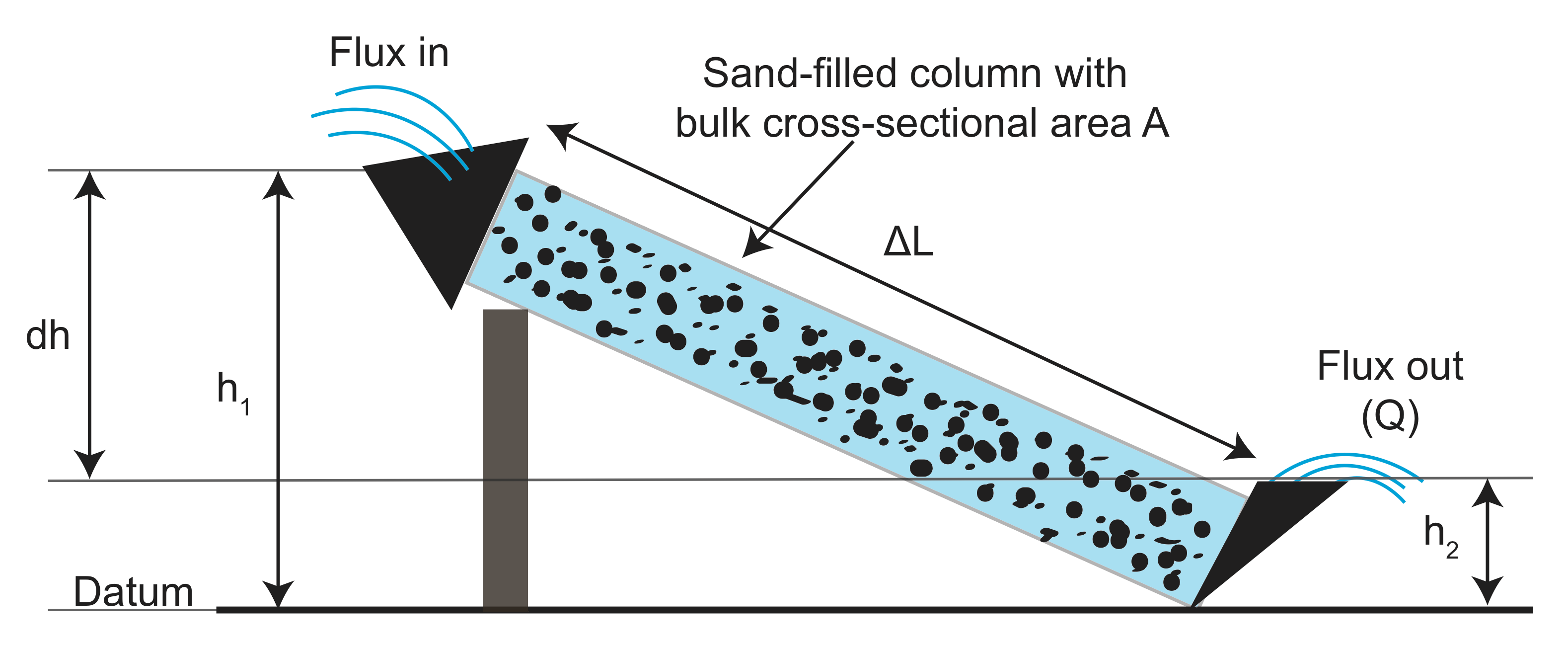
実験から,樋の長さに関するデータを収集しました(\(L\)),樋の断面積(\(A\)),高さ差(\(h_1-h_2\)),と出てくる水 次に、面積と樋の長さとの高さ差の比（\(\frac{h_1-h_2}{l}\)）で正規化された磁束測定値をプロットしました。 彼が見つけたのは、線形関係があり、勾配は樋で使用した粒状材料に依存するということです。

\

ここで、\(K\)は水理導電率、\(\frac{dh}{dx}\)は水理勾配です。 総排出速度である\(Q\)は、時間あたりの水の体積である\(\frac{m^3}{s}\)の単位を持ちます。 負の符号は、流体がより高い値からより低い値に油圧勾配を（負の）流れ落ちるという事実によるものである。

水理導電率は、流体が材料の細孔空間をどれだけ簡単に移動できるかを説明する物理的パラメータです。

水理導電率は、流体が材料の細孔空間を Darcyの最初の実験では、彼は異なる粒径の砂を使用しましたが、ほとんどの岩石にはいくつかの細孔空間があるため、固体岩石についても水理導電率を

Darcyの元の実験に続いて、有効な水理伝導率を決定する流体と岩石の物理的性質を理解するためのさらなる研究が行われました。 これらの実験から、

\

ここで、\(k\)は多孔質媒体（固体）の固有透磁率であり、\(\eta\)は流体の動的粘度であり、\(\gamma=\rho g\)は流体の比重であり、流体密度\(\rho\)と重力\(g\)に依存する。図中の強調表示された列はKであり、\(\frac{m}{s}\)の水伝導率です。 水圧伝導率は、darcysまたはcm2の単位で、固有の透磁率\(k\)の観点からも報告されることがあります。 水伝導率の値の全範囲は1-10-13\(\frac{m}{s}\)です。 Darcyのような実験は、実際の材料中のKを測定するために使用されます。

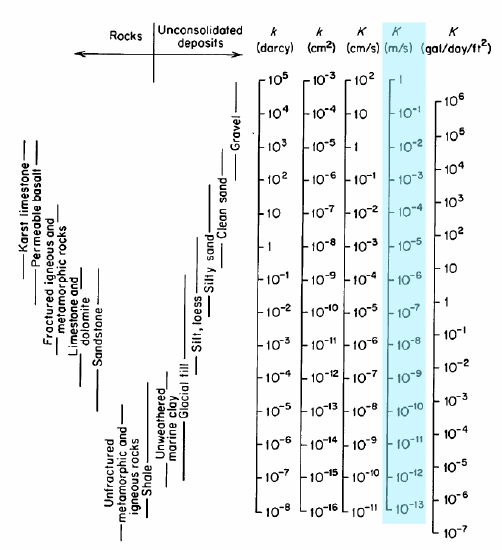Cherry,J.A,Taryn Lauschによって編集,Wikimedia経由)

放電速度\(Q\)はボリュームフラックスです(\(m^3/s\))しかし、我々は通常、速度または速度の観点から流体の流れを考えます。 放電の質問は、Darcyフラックス

\\]

または固有の透磁率と圧力勾配の観点から定義するために面積で割ることによって再配置することができます。

\

ここで\(\eta\)は流体粘度です（第二の方程式の導出については以下を参照）。

ダーシー流束は、速度の単位であっても、流体速度と等しくないことに注意することが重要です。 流体速度は、多孔質媒体を通るすべての可能な流体経路の速度の平均である平均線速度（\（v_a\））を介して見出される: しかし、この値を見つけることは、このクラスの範囲外です。 代わりに、流体速度は

\

ここで、\(\varphi\)は気孔率であり、vは流体速度です。 多孔度\(\varphi\)は、ボイド空間の体積と材料の総体積の比\(\varphi=\frac{V_{void}}{V_{tot}}\)として計算され、通常は0と1の間の分数またはパーセントとして表されます。 \(\Varphi\leq\)1の場合、流体速度はダーシー流束の方が大きいことに注意してください。

岩石や非固結材料を通る流れを議論するときに発生する別の用語は透水性です。 気孔率は岩石中の細孔（空隙）の実際の割合であるが、これらの空隙は異なる形状および異なる接続性を有することができ、これは流体が細孔空間を 透過性は、液体および気体が岩石を通過することができる容易さの尺度である。 材料がより強固になればなるほど、その透過性は低下する。 従って砂利のような”緩い”材料に高い透磁率がある。 いくつかの岩石はまた、流体が一方向に容易に流れることができるが、別の方向には流れないことを意味し、異方性透過性を有することができる。 異方性透磁率を有する岩石の例は頁岩である。 流体は、頁岩の層内で容易に移動することができますが、層を横切って移動することはできません。

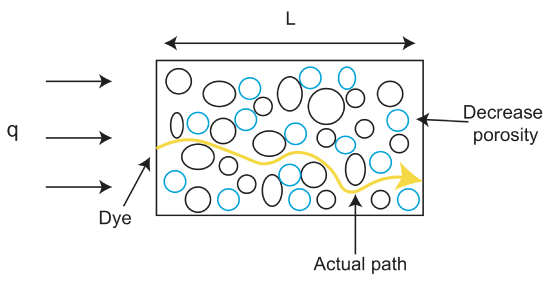
流体速度

のは、基本的な例をやってみましょう。私たちは、\(q=2\frac{m}{min}\)と\(\varphi\)が25%であり、流体速度を求めたいと考えています。最初に25％を0.25に変換します。

そして、\(v=\frac{2}{0.ここで、\(v=8\frac{m}{min}\)は流体速度です。\(v=8\frac{m}{min}\)は流体速度です。\(v=8\frac{m}{min}\)は流体速度です。\(v=8\frac{m}{min}\)は流体速度です。\(v=8\frac{m}{min}\)は

油圧ヘッド

ダーシーの実験に戻って、物理的なプロセスは、実際に樋を通って流体の流れを駆動しているものですか？\(\frac{dh}{dx}\)という用語は、油圧ヘッドと呼ばれ、これは、ある基準位置に対する流体の重量による液体圧力である：圧力勾配。\(\frac{dh}{dx}\)という用語は、\(\frac{dh}{dx}\)と呼ばれます。\(\frac{dh}{dx}\)という用語は、\(\frac{dh}{dx}\) しかし、\(\frac{dh}{dx}\)は単位長さあたりの圧力の単位を持っていないので、なぜそれは油圧ヘッドと呼ばれていますか？Darcyの実験では、水路の圧力が何であるかを考えてみましょう。

実験を行うために、Darcy’sは樋の上端に水のタンクを持っていて、樋の高さ\(h_1\)に相当する樋の上部に一定のレベルの水を提供していました。 同様に、底部には\(h_2\)に相当する一定レベルの水を持つタンクがありました。 したがって、水の重量による各タンク内の流体圧力は、\(P=\rho g h\)で与えられます。 プルームの上部と下部の間からの圧力勾配は、

\

または

\

ダーシーの法則に代入すると、

\&=\frac{K}{\rho g}\frac{dp}{dx}\end{align}です。 上から、水伝導率は、固有透磁率の観点から\(K=k\frac{\gamma}{\eta}\)と書くことができ、これは\(k\frac{\rho g}{\eta}\)または並べ替えと等価です。\(\frac{K}{\rho g}=\frac{k}{\eta}\)。 したがって、ダーシーの法則の用語の物理的起源は流体の圧力勾配であり、流れを駆動するため、\(\frac{dh}{dx}\)は油圧ヘッドと呼ばれます。

帯水層を離れる水

今、帯水層に入る水の流体速度を計算する例をやってみましょう。 帯水層の高さの下のスケッチでは、流れのある谷に隣接する丘の地形に従います。 水は高圧（頭の高さ）から谷に向かって流れ、ストリームで帯水層を残します。 ダーシーの法則を使用して、帯水層を形成する水の流れの速度を推定することができます。

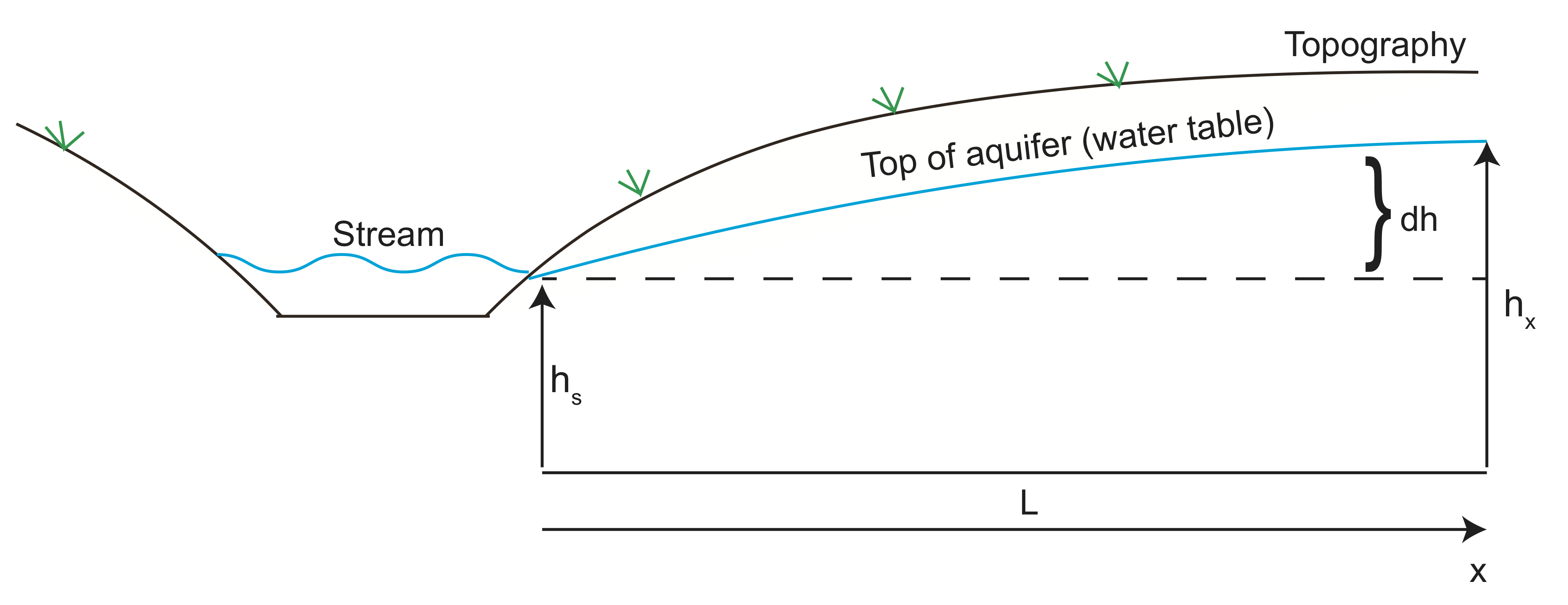
地球物理学的イメージングを使用して、帯水層の高さは、約100メートル（\（L\））離れた流れの高さの上に10メートル（\（dh\））であることが判明しました。 水伝導率が\(K=10^{-6}\)m/sで、気孔率が\(\varphi=30\)%であると仮定します。/p>

図\(\pageindex{7}\):ろうそくの炎からのプルームの層流から乱流への流れ(CC BY-SA3.0; Darcyの法則の暗黙の仮定の1つは、流れが層流であるということです。 層流は、すべて互いに平行に移動する流体の薄い層またはラミナからなることを特徴とする。 対照的に乱流は、流体の隣接する層が発散し、流れの下に異なる経路を取る渦巻き、渦および渦によって特徴付けられる。流体が層流であるか乱流であるかを定量化する方法の1つは、流れのレイノルズ数を計算することであり、次のように定義されます。

\

レイノルズ数は、流れの運動量バランスの2つの項を考慮することによって求められます。 最初の項は単位体積当たりの慣性力であり、流れを駆動します。\(\rho u\frac{du}{dx}\)。 2番目の項は単位体積当たりの粘性力であり、流れに抵抗します。\eta\frac{d^2u}{dx^2}\）。 これらの2つの用語はバランスをとる必要がありますので、それらを等しく設定することができます。

\

次に、変数の関連する次元のみをキャプ これを行うには、次元分析と呼ばれるものを通過し、各変数を参照値に置き換え、変数の非次元形式を掛けます。ここで、\(L\)は基準長さ（流体の深さ）であり、\(x’\)は非次元距離です。\(X\)は\(L x’\)のように書き換えられます。\(x\)は\(L x’\)のように書き換えられます。\(x\)は\(L x’\)のように書き換えられます。\(x’\)は\(L x’\)のように書き換えられます。\( 同様に、\(u=u_o u’\)とします。 これらを式に代入すると、

\

次に、前の定数値を組み合わせます

\

前の変数の組み合わせはレイノルズ数であることに注意してください

\

変数は\(u_o\)流速、l流体深さ、および前に見た変数、\(\rho\)流体密度、および\(\eta\)流体粘度である。 この解析を行うことにより，これら二つの項のバランスによって特徴づけられるフローは，単にレイノルズ数の値を知ることによって比較できることが分かった。 例えば、ある流れの粘度が別の流れの粘度の10倍である場合、二つの流れは同じように振る舞い、密度（または速度または長さ）も高い粘度の場合には10倍に増加する。ダーシー流を持つためには、レイノルズ数は約1-10（層流）未満でなければならない。 (Re>1-10\)の場合、流れは厳密には層流ではありませんが、まだ乱流ではありません（非線形、層流ではありません）。 乱流を持つためには、レイノルズの数は約2000以上でなければなりません。

分子と分母の定数が逆の方法で流れの特性に影響を与えることを理解すると、同様の外部条件下で異なる流体がどのように振る舞うかを考 例えば、速い速度を有する密度の高い流体は、より高いＲｅを有し、乱流挙動を示すであろう。 対照的に、高い粘度を有し、非常にゆっくりと移動する氷のような流体は、低いＲｅを有し、層流を有する可能性が高い。 氷の高粘度は、流れを安定させるために作用する。 別の例として、レイノルズ数\(\frac{\rho L}{\mu}\)の他の値が異なる場合、2つの流体が同じ速度で移動する可能性があると考えてください。 したがって、流れの種類は、流速だけでなく、レイノルズ数の変数の組み合わせに依存します。

ダーシーの流れの適用

ダーシーの法則は、帯水層と井戸の流れを支配する主な方程式です。 それがなければ、私たちは井戸を掘削したり、帯水層、特にカリフォルニアのセントラルバレーで水の動きを理解することはできません。p>