平均への回帰は、世界を観察するときに私たちを誤解させる可能性のある一般的な統計現象です。 平均への回帰がいつ機能しているかを認識することを学ぶことは、データを誤解したり、存在しないパターンを見たりするのを避けるのに役立ちます。

***

悪い判断のインスタンスを最小限に抑え、私たちの推論の弱点に対処することが重要です。 平均への回帰について学ぶことは私たちを助けることができます。

ノーベル賞を受賞した心理学者Daniel Kahnemanは、私たちの推論を曇らせ、現実に対する私たちの認識を歪める偏見についての本を書いた。 私たちの直感と脳は単純な統計をうまく扱っていないので、私たちがコミットする論理的なエラーのセット全体があることが判明しました。 彼が速くて遅いと考える際に調べるエラーの1つは、平均に向かって悪名高い回帰です。

平均への回帰の概念は、Francis Galtonによって最初に考案されました。 ルールは、チャンスが関与している多くの変数に依存している複雑な現象を持つ任意のシリーズでは、極端な結果は、より緩やかなものが続く傾向があ

知恵を求めて、ピーター-ベベリンは、新入社員のパフォーマンスに不満を持っていたジョンの例を提供しているので、彼は従業員のスキルを測定したスキ ジョンの結論：”スキル向上プログラムは、スキルの向上を引き起こしました。”これは必ずしも真実ではありません。 彼らの高いスコアは、平均への回帰の結果である可能性があります。 これらの個人は、スキルのスケールのローエンドにあるとして測定されたので、彼らはスキル向上プログラムを取っていなかった場合でも、改善を示してい ストレス、疲労、病気、気晴らしなど—そして、彼らの以前のパフォーマンスのための多くの理由がある可能性があります。 彼らの本当の能力はおそらく変わっていません。

私たちのパフォーマンスは、常にいくつかの平均的な真のパフォーマンスの周りに変化します。 極端なパフォーマンスは、次回はあまり極端になる傾向があります。 どうして？ テストの測定は決して厳密である場合もない。 すべての測定値は、1つの真の部分と1つのランダム誤差部分で構成されています。 測定値が極端である場合、それらは部分的に偶然によって引き起こされる可能性が高い。 チャンスは、我々はパフォーマンスを測定する二度目に少ない貢献する可能性があります。

私たちが失敗したという理由だけで何かをする方法から別の方法に切り替えると、新しい方法が同じか悪いかであっても、次回はより良いことこれは、データが分布を表すものではない可能性があるため、小さなサンプルサイズから外挿することが危険な理由の1つです。 また、James Marchは、誰かが仕事に長く滞在するほど、「観察されたパフォーマンスの記録と実際の能力の間の可能性の高い違いは少ない」と主張しています。”何かが特にスキルと運の組み合わせを含む任意の努力で、短期的に発生する可能性があります。 （スキルと運の比率は、平均への回帰にも影響します。”平均値への回帰は自然法則ではありません。 単に統計的傾向。 それが起こる前に、それは長い時間がかかることがあります。”

—Peter Bevelin

平均への回帰

平均への回帰の効果は、スポーツで頻繁に観察され、その効果は不当な推測をたくさん引き起こす。

速く、遅い考えることで、Kahnemanは人のスキージャンプ、最終的なスコアが2つの別々のジャンプの組合せである訓練を見ることをリコールする。 平均値への回帰に気づいて、カーネマンは、2回目のジャンプについての解説者の予測を聞いてびっくりしました。 彼は書いています:

ノルウェーは素晴らしい最初のジャンプを持っていた、彼は彼のリードを保護することを望んで、緊張し、おそらく悪化するだろう”または”ス

Kahnemanは、コメンテーターが平均への回帰に気づき、因果関係の証拠がない物語を思いついたと指摘している（物語の誤謬を参照）。 これは彼の話が真実ではないと言っているわけではありません。 たぶん、各ジャンプの前に心拍数を測定した場合、最初のジャンプが悪かった場合、彼らはよりリラックスしていることがわかります。 しかし、それはポイントではありません。 ポイントは、最初のジャンプの結果と同じように、運が役割を果たすときに平均への回帰が起こることです。

スポーツからの教訓は、チャンスが役割を果たすすべての活動に適用されます。 私達は頻繁にそれの進歩か欠乏に特定のプロセス上の私達の影響の説明を付ける。

実際には、パフォーマンスの科学は複雑で、状況に依存し、多くの場合、私たちがコントロール内にあると思うものの多くは本当にランダムです。

実際には、パフォーマンスの科学は複雑であり、状況に依存しています。

スキージャンプの場合、ジャンパーに対する強い風は、平凡な結果を示す最高のアスリートにもつながります。 同様に、平凡なジャンパーの賛成で強い風とスキーの条件は、彼の結果にかなりの、しかし一時的なバンプにつながる可能性があります。 しかしこれらの効果は条件が変われば消え、結果は常態に戻って退行します。

これは、コーチングとパフォーマンスの追跡のための深刻な影響を持つことができます。 回帰のルールは、パフォーマンスや雇用を評価するときに、特定の状況の結果よりも実績に頼らなければならないことを示唆しています。 そうでなければ、私たちは失望する傾向があります。

カーネマンが効果的な訓練の心理学についてイスラエル空軍に講義をしていたとき、役員の一人は、部下に賞賛を与えることはパフォーマンスを悪化させ、叱ることはその後の努力を改善させたという経験を共有した。 その結果、彼は負のフィードバックと寛大に成長していたし、あまりにも多くの賞賛を与えるのではなく警戒になっていました。Kahnemanはすぐに、それが職場の平均値への回帰であることを発見しました。

彼はあなたがあなた自身を試みたいと思う場合もある簡単な練習によって誤解を説明した。 彼は黒板に円を描き、その後、黒板に直面して自分の背中と円の中心にチョークの部分を投げるために役員を一つずつ尋ねました。 彼はその後、実験を繰り返し、第一および第二の試験で各役員のパフォーマンスを記録しました。当然のことながら、最初の試行で信じられないほどうまくいった人は、2回目の試行で悪化する傾向があり、その逆もありました。

もちろん、1回目の試行では非常にうまくいきました。 誤謬はすぐに明らかになりました：パフォーマンスの変化は自然に起こります。 それは再びフィードバックが全く問題ではないと言うことではありません–多分それはありませんが、役員はそれがしたと結論づける証拠はありませこの時点で、平均への回帰がなぜ起こるのか、そしてそれが発生したときにそれを認識していることを確認する方法を疑問に思うかもしれません。

平均への回帰を理解するためには、まず相関を理解する必要があります。

-1と1の間で変化する二つの尺度間の相関係数は、それらが共有する因子の相対的な重みの尺度である。

たとえば、ボトル入りの水の消費量と自殺率など、共有されている要因がほとんどない2つの現象は、0に近い相関係数を持つ必要があります。 つまり、世界のすべての国を見て、ボトル入りの水の一人当たりの消費量に対して特定の年の自殺率をプロットした場合、プロットはまったくパターン

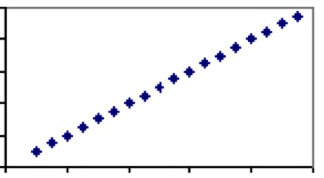
逆に、同じ要因にのみ依存する尺度があります。 これの良い例は温度です。 温度を決定する唯一の要因–分子の速度—はすべてのスケールで共有されているため、摂氏の各度は華氏で正確に1つの対応する値を持ちます。 したがって、摂氏と華氏の温度は1の相関係数を持ち、プロットは直線になります。

相関係数が1の人間科学の現象はほとんどありません。 しかし、関連が弱くて中程度であり、2つの現象の間にいくつかの説明力がある場所はたくさんあります。 身長と体重の間の相関関係を考えてみましょう。 実質的にすべての3歳は、すべての大人の男性よりも軽く、短くなりますが、すべての大人の男性や同じ高さの3歳が同じ重さになるわけではありません。

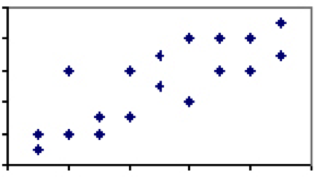
この変動と対応する相関の低い程度は、高さが一般的に良い予測子を言っている間、明らか 2つの測度の相関が完全でない場合は、平均への回帰の影響に注意する必要があります。Kahnemanは一般的なルールを観察しました：2つのスコア間の相関が不完全であるときはいつでも、平均への回帰があります。

Kahnemanは一般的なルールを観察しました。

これは最初は混乱し、あまり直感的ではないように見えるかもしれませんが、平均への回帰の程度は変数の相関の程度に直接関係しています。

この効果は簡単な例で説明することができます。

あなたがパーティーにいると仮定し、なぜ知的な女性が知的ではない男性と結婚する傾向があるのかを尋ねます。

あなたがパーティーにいると仮定し、 ほとんどの人、統計学の訓練を受けている人でさえ、競争の回避からこれらの女性が直面する孤独の恐怖まで、さまざまな因果関係の説明ですぐに このような論争の話題は、大きな議論を巻き起こす可能性があります。

さて、配偶者の知能スコア間の相関が完全ではない理由を尋ねたらどうなりますか？ この質問は興味深いものではなく、推測することはほとんどありません–私たちは皆、これが真実であることを知っています。 パラドックスは、2つの質問が代数的に等価であるという事実にあります。 Kahnemanは次のように説明しています：

配偶者の知性の相関が完全でない場合（そして、男性と女性が平均して知性に違いがない場合）、高度に知的な女性が平均よりも知的でない夫と結婚することは数学的必然性です（もちろんその逆もあります）。 平均値への観測された回帰は、不完全な相関よりも興味深いか説明可能ではありません。

相関が不完全であると仮定すると、任意の特性に関してトップ1％を表す二つのパートナーの可能性は、トップ1％を表す一つのパートナー

原因、効果、および治療

二つの要因の間に因果関係を確立しようとするとき、私たちは特に平均現象への回帰に注意する必要があります。

相関が不完全であるときはいつでも、最高は常に悪化するように見え、最悪は、追加の治療に関係なく、時間の経過とともに良くなるように見えます。 これは、一般的なメディア、時には訓練された科学者でさえ認識できないものです。

Kahnemanが与える例を考えてみましょう：

エネルギードリンクで治療されたうつ病の子供は、三ヶ月の期間にわたって大幅に改善します。 私はこの新聞の見出しを作ったが、それが報告する事実は本当です: あなたはエネルギードリンクでいくつかの時間のために落ち込んで子供のグループを治療した場合、彼らは臨床的に有意な改善を示すだろう。 また、頭の上に立ったり、一日二十分間猫を抱きしめたりする落ち込んでいる子供たちも改善を示すこともあります。

そのような見出しに出くわすたびに、エネルギードリンク、頭の上に立ったり、猫を抱きしめたりすることは、うつ病の完全に実行可能な治療法であるという結論にジャンプすることは非常に魅力的です。 しかし、これらのケースは再び平均への回帰を具現化しています:うつ病の子供たちは極端なグループであり、他のほとんどの子供たちよりも落ち込んでおり、極端なグループは時間の経過とともに平均に退行します。

うつ病の子供たちは極端なグループであり、他のほとんどの子供たちよりもうつ病であり、極端なグループは時間の経過とともに平均に退行します。 テストの連続した機会にうつ病のスコア間の相関は完璧ではないので、平均への回帰があります：うつ病の子供たちは、彼らが猫を抱きしめていなくても、レッドブルを飲まなくても、時間の経過とともに幾分良くなるでしょう。

極端なグループの変更がとにかく起こったとき、私たちはしばしば誤って特定のポリシーや治療を効果の原因とみなします。 これは根本的な問題を提示します：効果が実際のものであるか、単に変動性によるものであるかをどのように知ることができますか？幸いなことに、実際の改善と平均値への回帰の間で伝える方法があります。

幸いなことに、実際の改善と平均値への回帰の間で伝える方法があ それは、回帰単独で改善することが期待される、いわゆる対照群の導入である。 この研究の目的は、治療されたグループが回帰が説明できる以上に改善するかどうかを判断することです。

唯一の本当のベンチマークは、過去のパフォーマンスであり、対照群を導入することができない特定の個人やチームのパフォーマンスと実際の状況では、回帰の効果は解消することは不可能ではないにしても困難な場合があります。 業界平均、コホートグループの同輩、または過去の改善率と比較することができますが、これらのどれも完璧な尺度ではありません。

***

幸いなことに、平均現象自体への回帰の意識は、すでに運とパフォーマンスを理解するためのより慎重なアプローチに向けた素晴ら

平均への回帰から学ぶべきことがあれば、それは一度だけの成功事例に頼るのではなく、実績の重要性です。 私はあなたが偶然によって支配される部分的に極端な品質に遭遇する次回は、効果が時間をかけて退行する可能性があり、それに応じてあなたの期待を調整することを実現することを願っています。

次に読むもの

• 113の精神モデルであなたの思考をアップグレードする説明しました。
• あなたが否定的な結果を避けることができるように、第二レベルの思考について読みます。