La regressione verso la media è un fenomeno statistico comune che può ingannarci quando osserviamo il mondo. Imparare a riconoscere quando la regressione alla media è in gioco può aiutarci a evitare di interpretare erroneamente i dati e vedere modelli che non esistono.

***

È importante ridurre al minimo le istanze di cattivo giudizio e affrontare i punti deboli nel nostro ragionamento. Imparare a conoscere la regressione alla media può aiutarci.

Lo psicologo premio Nobel Daniel Kahneman ha scritto un libro sui pregiudizi che offuscano il nostro ragionamento e distorcono la nostra percezione della realtà. Si scopre che c’è tutta una serie di errori logici che commettiamo perché la nostra intuizione e il nostro cervello non si occupano bene di semplici statistiche. Uno degli errori che esamina nel pensare veloce e lento è la regressione infame verso la media.

La nozione di regressione alla media fu elaborata per la prima volta da Sir Francis Galton. La regola è che, in qualsiasi serie con fenomeni complessi che dipendono da molte variabili, in cui è coinvolta la possibilità, i risultati estremi tendono ad essere seguiti da quelli più moderati.

In Seeking Wisdom, Peter Bevelin offre l’esempio di John, che era insoddisfatto delle prestazioni dei nuovi dipendenti, quindi li ha inseriti in un programma di miglioramento delle abilità in cui ha misurato le abilità dei dipendenti:

I loro punteggi sono ora più alti di quelli del primo test. La conclusione di John: “Il programma di miglioramento delle abilità ha causato il miglioramento delle abilità.” Questo non è necessariamente vero. I loro punteggi più alti potrebbero essere il risultato della regressione alla media. Poiché questi individui sono stati misurati come sulla fascia bassa della scala di abilità, avrebbero mostrato un miglioramento anche se non avessero preso il programma di miglioramento delle abilità. E ci potrebbero essere molte ragioni per le loro prestazioni precedenti: stress, affaticamento, malattia, distrazione, ecc. La loro vera abilità forse non è cambiata.

Le nostre prestazioni variano sempre intorno ad alcune prestazioni reali medie. Le prestazioni estreme tendono a diventare meno estreme la prossima volta. Perché? Le misurazioni dei test non possono mai essere esatte. Tutte le misurazioni sono costituite da una parte vera e una parte di errore casuale. Quando le misurazioni sono estreme, è probabile che siano in parte causate dal caso. È probabile che il caso contribuisca meno alla seconda volta che misuriamo le prestazioni.

Se passiamo da un modo di fare qualcosa ad un altro solo perché non abbiamo successo, è molto probabile che facciamo meglio la prossima volta anche se il nuovo modo di fare qualcosa è uguale o peggiore.

Questo è uno dei motivi per cui è pericoloso estrapolare da campioni di piccole dimensioni, poiché i dati potrebbero non essere rappresentativi della distribuzione. È anche il motivo per cui James March sostiene che più a lungo qualcuno rimane nel proprio lavoro, “meno è probabile la differenza tra il record osservato di prestazioni e l’abilità effettiva.”Tutto può accadere nel breve periodo, specialmente in qualsiasi sforzo che implichi una combinazione di abilità e fortuna. (Il rapporto tra abilità e fortuna influisce anche sulla regressione alla media.)

Regressione alla media

Gli effetti della regressione alla media possono essere frequentemente osservati nello sport, dove l’effetto causa molte speculazioni ingiustificate.

Nel Pensare veloce e lento, Kahneman ricorda di guardare il salto con gli sci maschile, una disciplina in cui il punteggio finale è una combinazione di due salti separati. Consapevole della regressione alla media, Kahneman fu sorpreso di sentire le previsioni del commentatore sul secondo salto. Scrive:

La Norvegia ha avuto un ottimo primo salto; sarà teso, sperando di proteggere il suo vantaggio e probabilmente farà peggio” o “La Svezia ha avuto un brutto primo salto e ora sa di non avere nulla da perdere e sarà rilassato, il che dovrebbe aiutarlo a fare meglio.

Kahneman sottolinea che il commentatore aveva notato la regressione alla media e ha inventato una storia per la quale non c’erano prove causali (vedi fallacia narrativa). Questo non vuol dire che la sua storia non potrebbe essere vera. Forse, se misurassimo le frequenze cardiache prima di ogni salto, vedremmo che sono più rilassate se il primo salto fosse cattivo. Tuttavia, non è questo il punto. Il punto è che la regressione alla media avviene quando la fortuna gioca un ruolo, come ha fatto nel risultato del primo salto.

La lezione dello sport si applica a qualsiasi attività in cui il caso gioca un ruolo. Spesso attribuiamo spiegazioni della nostra influenza su un particolare processo al progresso o alla mancanza di esso.

In realtà, la scienza delle prestazioni è complessa, dipende dalla situazione e spesso molto di ciò che pensiamo sia sotto il nostro controllo è veramente casuale.

Nel caso di salti con gli sci, un forte vento contro il saltatore porterà anche il miglior atleta a mostrare risultati mediocri. Allo stesso modo, un forte vento e le condizioni di sci a favore di un ponticello mediocre possono portare a un notevole, ma un urto temporaneo nei suoi risultati. Questi effetti, tuttavia, scompariranno una volta che le condizioni cambiano e i risultati regrediranno di nuovo alla normalità.

Questo può avere gravi implicazioni per il coaching e il monitoraggio delle prestazioni. Le regole di regressione suggeriscono che quando si valutano le prestazioni o l’assunzione, dobbiamo fare affidamento sui track record più dei risultati di situazioni specifiche. Altrimenti, siamo inclini a rimanere delusi.

Quando Kahneman stava tenendo una conferenza all’Aviazione israeliana sulla psicologia dell’addestramento efficace, uno degli ufficiali ha condiviso la sua esperienza che estendere la lode ai suoi subordinati ha portato a prestazioni peggiori, mentre il rimprovero ha portato a un miglioramento negli sforzi successivi. Di conseguenza, era cresciuto fino a essere generoso con un feedback negativo ed era diventato piuttosto diffidente nel dare troppe lodi.

Kahneman notò immediatamente che si trattava di regressione alla media al lavoro. Ha illustrato l’idea sbagliata con un semplice esercizio si consiglia di provare voi stessi. Disegnò un cerchio su una lavagna e poi chiese agli ufficiali uno per uno di gettare un pezzo di gesso al centro del cerchio con le spalle rivolte verso la lavagna. Ha poi ripetuto l’esperimento e registrato le prestazioni di ogni ufficiale nel primo e nel secondo processo.

Naturalmente, quelli che hanno fatto incredibilmente bene al primo tentativo tendevano a fare peggio al secondo tentativo e viceversa. L’errore divenne immediatamente chiaro: il cambiamento delle prestazioni avviene naturalmente. Che ancora una volta non vuol dire che il feedback non importa a tutti – forse lo fa, ma l’ufficiale non aveva prove per concludere lo ha fatto.

La correlazione imperfetta e la possibilità

A questo punto, potresti chiederti perché avviene la regressione alla media e come possiamo assicurarci di esserne consapevoli quando si verifica.

Per comprendere la regressione alla media, dobbiamo prima capire la correlazione.

Il coefficiente di correlazione tra due misure che varia tra -1 e 1, è una misura del peso relativo dei fattori che condividono. Ad esempio, due fenomeni con pochi fattori condivisi, come il consumo di acqua in bottiglia rispetto al tasso di suicidio, dovrebbero avere un coefficiente di correlazione vicino a 0. Vale a dire, se guardassimo tutti i paesi del mondo e tracciassimo i tassi di suicidio di un anno specifico rispetto al consumo pro capite di acqua in bottiglia, la trama non mostrerebbe alcun modello.

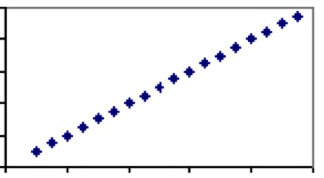
al contrario, ci sono misure che dipendono esclusivamente dal fattore stesso. Un buon esempio di questo è la temperatura. L’unico fattore che determina la temperatura – la velocità delle molecole — è condiviso da tutte le scale, quindi ogni grado in Celsius avrà esattamente un valore corrispondente in Fahrenheit. Pertanto la temperatura in Celsius e Fahrenheit avrà un coefficiente di correlazione di 1 e la trama sarà una linea retta.

Ci sono pochi fenomeni nelle scienze umane che hanno un coefficiente di correlazione pari a 1. Ci sono, tuttavia, un sacco in cui l’associazione è da debole a moderata e c’è un certo potere esplicativo tra i due fenomeni. Considera la correlazione tra altezza e peso, che atterrerebbe da qualche parte tra 0 e 1. Mentre praticamente ogni bambino di tre anni sarà più leggero e più corto di ogni uomo adulto, non tutti gli uomini adulti o bambini di tre anni della stessa altezza peseranno lo stesso.

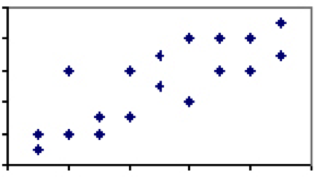
Questa variazione e la corrispondente minore grado di correlazione indica che, mentre l’altezza è in generale un buon predittore, ci sono chiaramente altri fattori oltre l’altezza a giocare. Quando la correlazione di due misure è meno che perfetta, dobbiamo fare attenzione agli effetti della regressione alla media.

Kahneman ha osservato una regola generale: ogni volta che la correlazione tra due punteggi è imperfetta, ci sarà una regressione alla media.

Questo all’inizio potrebbe sembrare confuso e non molto intuitivo, ma il grado di regressione alla media è direttamente correlato al grado di correlazione delle variabili. Questo effetto può essere illustrato con un semplice esempio.

Si supponga di essere a una festa e chiedere perché è che le donne altamente intelligenti tendono a sposare uomini che sono meno intelligenti di quanto non siano. La maggior parte delle persone, anche quelli con una certa formazione in statistica, salterà rapidamente con una varietà di spiegazioni causali che vanno da evitare la concorrenza ai timori di solitudine che queste femmine devono affrontare. Un argomento di tale controversia rischia di suscitare un grande dibattito.

Ora, cosa succede se abbiamo chiesto perché la correlazione tra i punteggi di intelligenza dei coniugi è meno che perfetta? Questa domanda non è altrettanto interessante e c’è poco da indovinare – sappiamo tutti che questo è vero. Il paradosso sta nel fatto che le due domande sono algebricamente equivalenti. Kahneman, spiega:

Se la correlazione tra l’intelligenza dei coniugi è meno che perfetto (e se gli uomini e le donne, in media, non differiscono in intelligenza), allora è un matematico inevitabilità che molto intelligente con donne sposate a uomini che sono mediamente meno intelligenti di quello che sono (e viceversa, naturalmente). La regressione osservata alla media non può essere più interessante o più spiegabile della correlazione imperfetta.

Supponendo che la correlazione sia imperfetta, le probabilità che due partner rappresentino l ‘1% superiore in termini di qualsiasi caratteristica sono molto più piccole di un partner che rappresenta l’ 1% superiore e l’altro – il 99% inferiore.

La causa, l’effetto e il trattamento

Dovremmo essere particolarmente cauti della regressione al fenomeno medio quando cerchiamo di stabilire la causalità tra due fattori. Ogni volta che la correlazione è imperfetta, il meglio sembrerà sempre peggiorare e il peggio sembrerà migliorare nel tempo, indipendentemente da qualsiasi trattamento aggiuntivo. Questo è qualcosa che i media generali e talvolta anche gli scienziati addestrati non riescono a riconoscere.

Si consideri l’esempio dato da Kahneman:

I bambini depressi trattati con una bevanda energetica migliorano significativamente in un periodo di tre mesi. Ho inventato questo titolo di giornale, ma il fatto che riporta è vero: se hai trattato un gruppo di bambini depressi per qualche tempo con una bevanda energetica, mostrerebbero un miglioramento clinicamente significativo. È anche il caso che i bambini depressi che trascorrono un po ‘ di tempo in piedi sulla testa o abbracciano un gatto per venti minuti al giorno mostrino anche miglioramenti.

Ogni volta che si imbattono in tali titoli è molto allettante saltare alla conclusione che le bevande energetiche, in piedi sulla testa o abbracciando i gatti sono tutte cure perfettamente praticabili per la depressione. Questi casi, tuttavia, incarnano ancora una volta la regressione alla media:

I bambini depressi sono un gruppo estremo, sono più depressi della maggior parte degli altri bambini—e i gruppi estremi regrediscono alla media nel tempo. La correlazione tra i punteggi di depressione nelle successive occasioni di test è meno che perfetta, quindi ci sarà una regressione alla media: i bambini depressi miglioreranno un po ‘ nel tempo anche se non abbracciano gatti e non bevono Red Bull.

Spesso attribuiamo erroneamente una politica o un trattamento specifico come causa di un effetto, quando il cambiamento nei gruppi estremi sarebbe avvenuto comunque. Questo presenta un problema fondamentale: come possiamo sapere se gli effetti sono reali o semplicemente dovuti alla variabilità?

Fortunatamente c’è un modo per dire tra un miglioramento reale e la regressione alla media. Questa è l’introduzione del cosiddetto gruppo di controllo, che dovrebbe migliorare solo con la regressione. Lo scopo della ricerca è determinare se il gruppo trattato migliora più di quanto la regressione possa spiegare.

In situazioni di vita reale con le prestazioni di individui o team specifici, dove l’unico vero benchmark è la performance passata e nessun gruppo di controllo può essere introdotto, gli effetti della regressione possono essere difficili se non impossibili da districare. Possiamo confrontarci con la media del settore, i pari nel gruppo di coorte o i tassi storici di miglioramento, ma nessuna di queste sono misure perfette.

***

Fortunatamente la consapevolezza della regressione al fenomeno medio è già un ottimo primo passo verso un approccio più attento alla comprensione della fortuna e delle prestazioni.

Se c’è qualcosa da imparare dalla regressione alla media, è l’importanza dei track record piuttosto che affidarsi a storie di successo una tantum. Spero che la prossima volta che vi imbattete in una qualità estrema in parte governata dal caso vi renderete conto che gli effetti sono suscettibili di regredire nel tempo e regolerà le vostre aspettative di conseguenza.

Cosa leggere dopo

• Aggiorna il tuo pensiero con 113 modelli mentali spiegati.
• Leggi il pensiero di secondo livello in modo da poter evitare conseguenze negative.