Nota del redattore

Il seguente rapporto di ricerca degli studenti è stato preparato per la classe Math 255 del professor Judit Kardos, tenuta al College of New Jersey. Questo è stato un corso introduttivo di 3 crediti nella Storia della matematica. Questo rapporto è stato conteggiato verso il 30% del voto finale. È un esempio del tipo di ricerca storica che gli studenti possono fare usando fonti secondarie.

La soluzione di Leonard Euler al problema del ponte di Königsberg

Königsberg

La nostra storia inizia nel xviii secolo, nella pittoresca città di Königsberg, in Prussia, sulle rive del fiume Pregel. Nel 1254, i cavalieri teutonici fondarono la città di Königsberg sotto la guida del re boemo Ottoker II dopo la loro seconda crociata contro i prussiani. Nel Medioevo, Königsberg divenne una città molto importante e centro commerciale con la sua posizione strategicamente posizionata sul fiume. Le opere d’arte del XVIII secolo mostrano Königsberg come una città fiorente, dove flotte di navi riempiono il Pregel, e il loro commercio offre uno stile di vita confortevole sia ai mercanti locali che alle loro famiglie. L’economia sana ha permesso alla gente della città di costruire sette ponti attraverso il fiume, la maggior parte dei quali collegati all’isola di Kneiphof; le loro posizioni possono essere viste nell’immagine di accompagnamento .

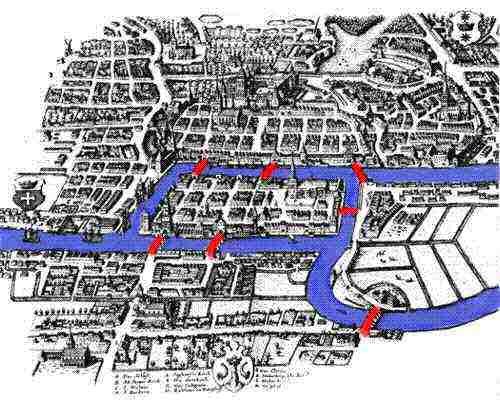
Mentre il fiume scorreva intorno a Kneiphof, che letteralmente significa pub yard, e un’altra isola, divideva la città in quattro regioni distinte. I sette ponti erano chiamati Ponte del fabbro, Ponte di collegamento, Ponte verde, Ponte del Commerciante, Ponte di legno, Ponte alto e Ponte del miele. Secondo la tradizione, i cittadini di Königsberg passavano la domenica pomeriggio passeggiando per la loro bella città. Mentre si cammina, la gente della città ha deciso di creare un gioco per se stessi, il loro obiettivo è quello di escogitare un modo in cui potevano camminare per la città, attraversando ciascuno dei sette ponti solo una volta. Anche se nessuno dei cittadini di Königsberg poteva inventare un percorso che permettesse loro di attraversare ciascuno dei ponti solo una volta, tuttavia non potevano dimostrare che era impossibile. Fortunatamente per loro, Königsberg non era troppo lontano da San Pietroburgo, casa del famoso matematico Leonard Euler.

Eulero e il problema del ponte

Perché Eulero si dovrebbe preoccupare di un problema così estraneo al campo della matematica? Perché un così grande matematico trascorrerebbe molto tempo con un problema banale come il problema del ponte di Königsberg? Eulero era ovviamente un uomo impegnato, pubblicando più di 500 libri e documenti durante la sua vita. Nel 1775 da solo, ha scritto una media di una carta matematica a settimana, e durante la sua vita ha scritto su una varietà di argomenti oltre alla matematica, tra cui meccanica, ottica, astronomia, navigazione, e idrodinamica. Non sorprende che Eulero ritenesse che questo problema fosse banale, affermando in una lettera del 1736 a Carl Leonhard Gottlieb Ehler, sindaco di Danzica, che gli chiedeva una soluzione al problema :

. . . Così vedete, nobilissimo Signore, come questo tipo di soluzione abbia poca relazione con la matematica, e non capisco perché ci si aspetti che un matematico la produca, piuttosto che chiunque altro, poiché la soluzione si basa sulla sola ragione, e la sua scoperta non dipende da alcun principio matematico. Per questo motivo, non so perché anche le domande che hanno così poco rapporto con la matematica siano risolte più rapidamente dai matematici che da altri.

Anche se Eulero trovò il problema banale, ne rimase comunque incuriosito. In una lettera scritta lo stesso anno a Giovanni Marinoni, un matematico e ingegnere italiano, Eulero disse:

Questa domanda è così banale, ma mi sembrava degna di attenzione in quanto la geometria, né l’algebra, né l’arte del conteggio erano sufficienti per risolverla.

Eulero credeva che questo problema fosse legato a un argomento che Gottfried Wilhelm Leibniz aveva discusso e desiderava lavorare, qualcosa che Leibniz chiamava geometria situs, o geometria della posizione. Questa cosiddetta geometria della posizione è quella che ora viene chiamata teoria dei grafi, che Eulero introduce e utilizza mentre risolve questo famoso problema.

La prova di Eulero

Il 26 agosto 1735, Eulero presenta un documento contenente la soluzione al problema del ponte di Konigsberg. Affronta sia questo problema specifico, sia una soluzione generale con qualsiasi numero di masse terrestri e qualsiasi numero di ponti. Questo documento, chiamato ‘Solutio problematis ad geometriam situs pertinentis,’ è stato poi pubblicato nel 1741 . Il documento di Eulero è diviso in ventuno paragrafi numerati e, in quello che segue, verrà presentata una versione semplificata dei paragrafi di Eulero.

Nei primi due paragrafi della dimostrazione di Eulero, introduce il problema del ponte di Konigsberg. Nel paragrafo 1, Eulero afferma che egli ritiene che questo problema riguarda la geometria, ma non la geometria ben noto dai suoi contemporanei, che coinvolge misure e calcoli, ma invece un nuovo tipo di geometria, che Leibniz indicato come Geometria di posizione. Quindi, nel paragrafo 2, Eulero spiega al suo pubblico come funziona il problema di Konigsberg. Eulero fornì uno schizzo del problema (vedi Figura 1 di Eulero), e chiamò i sette ponti distinti: a, b, c, d, e, f, e, g. In questo paragrafo afferma la domanda generale del problema, “Si può scoprire se è possibile attraversare ogni ponte esattamente una volta?”

Figura 1 di Eulero da ‘Solutio problematis ad geometriam situs pertinentis,’ Eneström 53

Dopo aver indicato la questione generale che sta cercando di risolvere, Eulero inizia ad esplorare diversi metodi per trovare una soluzione. Nel paragrafo 3, Eulero dice al lettore che per risolvere questo problema specifico, potrebbe scrivere tutti i percorsi possibili, ma questa tecnica richiederebbe molto tempo e non funzionerebbe per configurazioni più grandi con più ponti e masse terrestri. A causa di questi problemi, Eulero ha deciso di scegliere un metodo diverso per risolvere questo problema.

Nel paragrafo 4, inizia a semplificare il problema inventando un comodo sistema per rappresentare l’attraversamento di un ponte. Eulero decide che invece di usare le lettere minuscole per rappresentare l’attraversamento di un ponte avrebbe scritto le lettere maiuscole che rappresentano le masse terrestri. Per esempio, facendo riferimento alla sua Figura 1, AB significherebbe un viaggio che è iniziato in massa A, e si è conclusa in B. Inoltre, se dopo aver viaggiato da massa A a B, qualcuno decide di passare a massa D, questo sarebbe semplicemente indicato, ABD. Nel paragrafo 5, Eulero continua la sua discussione su questo processo spiegando che in ABDC, sebbene ci siano quattro lettere maiuscole, sono stati attraversati solo tre ponti. Eulero spiega che non importa quanti ponti ci siano, ci sarà un’altra lettera per rappresentare l’incrocio necessario. Per questo motivo, l’intero problema del ponte di Königsberg richiedeva sette ponti da attraversare, e quindi otto lettere maiuscole.

Nel paragrafo 6, Eulero continua a spiegare i dettagli del suo metodo. Dice al lettore che se c’è più di un ponte che può essere attraversato quando si passa da una massa all’altra, non importa quale ponte viene utilizzato. Ad esempio, anche se ci sono due ponti, a e b, che possono portare un viaggiatore da A a B, non importa con la notazione di Eulero quale ponte è preso. In questo paragrafo, Eulero discute anche il problema specifico che sta affrontando. Spiega, usando la sua figura originale, che il problema di Königsberg ha bisogno esattamente di otto lettere,dove le coppie di (A,B) e (A, C) devono apparire l’una accanto all’altra esattamente due volte, indipendentemente dalla lettera che appare per prima. Inoltre, le coppie (A,D), (B,D) e (C, D) devono verificarsi insieme esattamente una volta per un percorso che attraversa ogni ponte una volta e solo una volta per esistere.

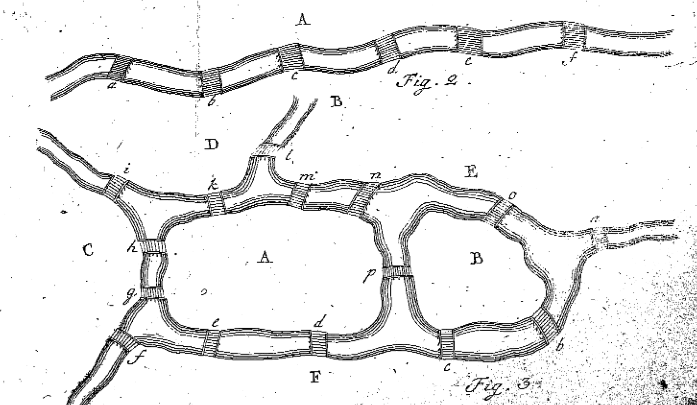
Le figure 2 e 3 di Eulero da ‘Solutio problematis ad geometriam situs pertinentis,’ Eneström 53

Nel paragrafo 7, Eulero informa il lettore che o deve trovare una sequenza di otto lettere che soddisfi il problema, oppure deve dimostrare che tale sequenza non esiste. Prima di farlo per il problema del ponte di Königsberg, decide di trovare una regola per scoprire se esiste un percorso per un problema più generale. Lo fa nel paragrafo 8 guardando molto più semplice esempio di masse terrestri e ponti. Eulero disegna la figura 2 e inizia a valutare le situazioni in cui la regione A viene percorsa. Eulero afferma che se il ponte a viene percorso una volta, A era dove il viaggio iniziava o terminava, e quindi veniva usato solo una volta. Se i ponti a, b e c sono tutti percorsi una volta, A viene utilizzato esattamente due volte, indipendentemente dal fatto che sia il punto di partenza o di fine. Allo stesso modo, se cinque ponti portano ad A, la massa terrestre A si verificherebbe esattamente tre volte nel viaggio. Eulero afferma che, ” In generale, se il numero di ponti è qualsiasi numero dispari, e se è aumentato di uno, allora il numero di occorrenze di A è la metà del risultato.”In altre parole, se c’è un numero dispari di ponti che collegano A ad altre masse terrestri, aggiungi uno al numero di ponti e dividilo per due, per scoprire quante volte totali A deve essere usato nel percorso, dove ogni ponte viene usato una volta e solo una volta (cioè Occorrenze totali di A dove A ha un numero dispari di ponti = (#di ponti-1) / 2).

Usando questo fatto Eulero risolve il problema del ponte di Königsberg nel paragrafo 9. In tal caso, poiché ci sono cinque ponti che portano ad A, deve verificarsi tre volte (vedi la sua Figura 1, sopra). Allo stesso modo, B, C e D devono apparire due volte poiché hanno tutti tre ponti che portano a loro. Quindi 3(per A) + 2(per B) + 2(per C) + 2 (per D) = 9, ma Eulero ha già affermato che ci devono essere solo otto occorrenze per i sette ponti. Questa è una contraddizione! Pertanto, è impossibile percorrere i ponti nella città di Königsberg una volta e solo una volta. La fine, o è? Mentre la gente di Königsberg può essere felice con questa soluzione, il grande matematico Leonhard Eulero non era soddisfatto. Eulero continua ulteriormente la sua prova per affrontare situazioni più generali.

Generalizzazione di Eulero

Nel paragrafo 10, Eulero continua la sua discussione notando che se la situazione coinvolge tutte le masse terrestri con un numero dispari di ponti, è possibile dire se un viaggio può essere fatto usando ogni ponte solo una volta. Eulero afferma che se la somma del numero di volte in cui ogni lettera deve apparire è una in più del numero totale di ponti, si può fare un viaggio. Tuttavia, se il numero di eventi è maggiore di uno in più rispetto al numero di ponti, non è possibile effettuare un viaggio, come il problema del ponte di Königsberg. Questo perché la regola, che Eulero dà per un numero dispari di ponti, usando la sua Figura 2, è vera per la situazione generale se c’è solo un’altra massa terrestre o più di una.

Nei paragrafi 11 e 12, Eulero tratta la situazione in cui una regione ha un numero pari di ponti ad essa collegati. Questa situazione non appare nel problema di Königsberg e, quindi, è stata ignorata fino ad ora. Nella situazione con una massa X con un numero pari di ponti, possono verificarsi due casi. Il primo caso è quando X è il punto di partenza per il viaggio. In questo caso, X apparirà due volte, una volta come punto di partenza e di nuovo come punto finale. Nell’altro caso, X non è il punto di partenza. Se ciò dovesse accadere, X apparirebbe solo una volta, poiché il viaggio dovrebbe entrare attraverso un ponte e uscire immediatamente attraverso l’unico altro disponibile. Allo stesso modo, se ci sono quattro ponti collegati a X, il numero di occorrenze di X dipende dal fatto che sia o meno un punto di partenza. Se il viaggio inizia in X, deve apparire tre volte, ma se non inizia in X, apparirà solo due volte. Quindi, in generale, se X ha un numero pari di ponti collegati, allora se il viaggio non inizia in X, X appare la metà del numero di volte come ponti (cioè Occorrenze di X dove X è pari e non il punto di partenza = (#di ponti) / 2). Se il viaggio inizia in X, X appare metà del numero di volte come ponti, più uno (cioè Occorrenze di X dove X è pari e punto di partenza = ((#di ponti) / 2) + 1).

Nei paragrafi da 13 a 15, Eulero spiega come capire se un percorso che utilizza ogni ponte una volta e solo una volta esiste e presenta il proprio esempio per mostrare come funziona. Eulero spiega innanzitutto il suo semplice metodo in sei fasi per risolvere qualsiasi situazione generale con masse terrestri divise da fiumi e collegate da ponti. In primo luogo Eulero denota ogni massa terrestre con una lettera maiuscola. In secondo luogo prende il numero totale di ponti, ne aggiunge uno e lo scrive sopra il grafico che sta per fare. Successivamente, prende le lettere maiuscole, le mette in una colonna e accanto a loro scrive il numero di ponti. In quarto luogo, indica con asterischi le masse terrestri che hanno un numero pari di ponti. Quindi, accanto a ciascun numero pari, scrive ½ del numero e accanto a ciascun numero dispari posiziona ½ il numero più uno. Infine, Eulero aggiunge i numeri scritti nella colonna più a destra e se la somma è inferiore o uguale al numero di ponti più uno, allora il viaggio richiesto è possibile. È importante notare tuttavia che se la somma è inferiore al numero di ponti più uno, il viaggio deve iniziare da una delle masse terrestri contrassegnate da un asterisco. Se la somma è uguale al numero di ponti più uno, il viaggio deve iniziare in una regione non contrassegnata da un asterisco.

Esempi

Usando il problema Konigsberg come primo esempio Eulero mostra quanto segue:

Numero di ponti = 7, Numero di ponti più uno = 8

Regione Ponti Volte la Regione Deve Apparire

5 3

B 3 2

C 3 2

D 3 2

Tuttavia, 3 + 2 + 2 + 2 = 9, che è più di 8, così il viaggio è impossibile.

Poiché questo esempio è piuttosto semplice, Eulero decide di progettare la propria situazione con due isole, quattro fiumi e quindici ponti. La situazione creata da Eulero può essere vista nella sua Figura 3, sopra. Eulero ora tenta di capire se esiste un percorso che consente a qualcuno di superare ogni ponte una volta e solo una volta. Eulero segue la stessa procedura come sopra, la denominazione di cinque diverse regioni con le lettere maiuscole, e crea una tabella per verificare se è possibile, come la seguente:

Numero di ponti = 15, Numero di ponti più uno = 16

Regione Ponti Volte la Regione Deve Apparire

* 8 4

B* 4 2

C* 4 2

D 3 2

E 5 3

F* 6 3

In aggiunta, 4 + 2 + 2 + 2 + 3 + 3 = 16, che equivale al numero di ponti, più uno, il che significa che il viaggio è, infatti, possibile. Poiché la somma è uguale al numero di ponti più uno, il viaggio deve iniziare in D o E. Ora che Eulero sa che è possibile fare un viaggio, tutto ciò che deve fare è indicare quale sarà il percorso. Eulero sceglie il percorso EaFbBcFdAeFfCgAhCiDkAmEnApBoElD, dove include quali ponti sono incrociati tra le lettere che rappresentano le masse terrestri. Sebbene questa informazione sia estranea, poiché il ponte esatto non ha importanza nel sapere che un viaggio è possibile, è utile quando si seleziona un percorso. Questo è un buon esempio che mostra il metodo che Eulero userebbe quando risolverebbe qualsiasi problema di questa natura.

Conclusioni di Eulero

Nei prossimi paragrafi, Eulero presenta un altro modo per capire se un viaggio può essere fatto dato qualsiasi insieme di masse terrestri, ponti e fiumi. Nel paragrafo 16, Eulero sottolinea che il totale dei numeri elencati direttamente a destra delle masse terrestri aggiunge fino al doppio del numero totale di ponti. Questo fatto in seguito diventa noto come lemma della stretta di mano. Fondamentalmente, il lemma handshaking afferma che ogni ponte viene contato due volte, una volta per ogni massa terrestre a cui è collegato. Nel paragrafo 17, Eulero afferma che la somma di tutti i ponti che portano a ciascuna regione è pari, poiché la metà di questo numero è uguale al numero totale di ponti. Tuttavia, questo è impossibile se ci sono un numero dispari di masse terrestri con un numero dispari di ponti. Pertanto, Eulero dimostra che se ci sono alcuni numeri dispari collegati alle masse terrestri, ci deve essere un numero pari di queste masse terrestri.

Tuttavia, questo non è sufficiente per dimostrare quando c’è un percorso in cui ogni ponte viene usato una volta e solo una volta, poiché il problema del ponte di Königsberg ha un numero pari di masse terrestri con un numero dispari di ponti che vanno a loro. A causa di ciò, Eulero aggiunge ulteriori restrizioni nei paragrafi 18 e 19. Eulero spiega che poiché il totale dei numeri di ponti collegati a ciascuna massa terrestre è uguale al doppio del numero di ponti (come si vede nel lemma di handshaking), quindi se aggiungi due a questa somma e poi dividi per due, otterrai il numero di ponti totali più uno. Questo numero è lo stesso di quello usato prima, che viene usato per dire se un percorso è possibile. Se tutti i numeri sono pari, la terza colonna della tabella sommerà a uno in meno del numero totale di ponti più uno.

Eulero spiega quindi che è ovvio che se ci sono due masse terrestri con un numero dispari di ponti, il viaggio sarà sempre possibile se il viaggio inizia in una delle regioni con un numero dispari di ponti. Questo perché se i numeri pari sono dimezzati e ciascuno di quelli dispari è aumentato di uno e dimezzato, la somma di queste metà sarà uguale a uno in più del numero totale di ponti. Tuttavia, se ci sono quattro o più masse terrestri con un numero dispari di ponti, allora è impossibile che ci sia un percorso. Questo perché la somma delle metà dei numeri dispari più uno insieme alla somma di tutte le metà dei numeri pari renderà la somma della terza colonna maggiore del numero totale di ponti più uno. Pertanto, Eulero ha appena dimostrato che ci possono essere al massimo due masse terrestri con un numero dispari di ponti.

Con questo detto, Eulero può ora trarre le sue conclusioni riguardanti forme più generali del problema del ponte di Königsberg. Nel paragrafo 20, Eulero fornisce le tre linee guida che qualcuno può usare per capire se esiste un percorso usando ogni ponte una volta e una sola volta. In primo luogo, ha affermato che se ci sono più di due masse terrestri con un numero dispari di ponti, allora questo viaggio non è possibile. In secondo luogo, se il numero di ponti è dispari per esattamente due masse terrestri, allora il viaggio è possibile se inizia in una delle due masse terrestri dispari. Infine, Eulero afferma che se non ci sono regioni con un numero dispari di masse terrestri, il viaggio può essere compiuto a partire da qualsiasi regione. Dopo aver affermato questi tre fatti, Eulero conclude la sua prova con il paragrafo 21, che afferma semplicemente che dopo aver capito che esiste un percorso, devono ancora passare attraverso lo sforzo di scrivere un percorso che funzioni. Eulero credeva che il metodo per realizzare questo era banale, e non voleva spendere una grande quantità di tempo su di esso. Tuttavia, Eulero suggerì di concentrarsi su come spostarsi da una massa all’altra, invece di concentrarsi inizialmente sui ponti specifici.

La dimostrazione e la teoria dei grafi di Eulero

Leggendo la dimostrazione originale di Eulero, si scopre un lavoro di matematica relativamente semplice e facilmente comprensibile; tuttavia, non è la prova effettiva ma i passaggi intermedi che rendono famoso questo problema. La grande innovazione di Eulero fu nel vedere il problema del ponte di Königsberg in modo astratto, usando linee e lettere per rappresentare la situazione più ampia di masse terrestri e ponti. Ha usato lettere maiuscole per rappresentare masse terrestri, e lettere minuscole per rappresentare ponti. Questo è stato un tipo completamente nuovo di pensiero per il tempo, e nel suo articolo, Eulero accidentalmente scatenato un nuovo ramo della matematica chiamato teoria dei grafi, dove un grafico è semplicemente una raccolta di vertici e spigoli. Oggi un percorso in un grafico, che contiene ogni bordo del grafico una volta e solo una volta, è chiamato un percorso euleriano, a causa di questo problema. Dal momento in cui Eulero ha risolto questo problema ad oggi, la teoria dei grafi è diventata una branca importante della matematica, che guida la base del nostro pensiero sulle reti.

Il problema del ponte di Königsberg è il motivo per cui Biggs afferma,

Le origini della teoria dei grafi sono umili, persino frivole The I problemi che hanno portato allo sviluppo della teoria dei grafi erano spesso poco più che enigmi, progettati per testare l’ingegno piuttosto che stimolare l’immaginazione. Ma nonostante l’apparente banalità di tali enigmi, hanno catturato l’interesse dei matematici, con il risultato che la teoria dei grafi è diventata un argomento ricco di risultati teorici di una sorprendente varietà e profondità.

Come implicherebbe l’affermazione di Biggs, questo problema è così importante che è menzionato nel primo capitolo di ogni libro di Teoria dei grafi che è stato esaminato nella libreria.

Dopo la scoperta di Eulero (o invenzione, a seconda di come il lettore lo guarda), teoria dei grafi boom con importanti contributi fatti da grandi matematici come Augustin Cauchy, William Hamilton, Arthur Cayley, Gustav Kirchhoff, e George Polya. Questi uomini hanno tutti contribuito a scoprire ” quasi tutto ciò che si sa su grafici grandi ma ordinati, come il reticolo formato da atomi in un cristallo o il reticolo esagonale fatto dalle api in un alveare .”Altri famosi problemi di teoria dei grafi includono trovare un modo per fuggire da un labirinto o labirinto, o trovare l’ordine delle mosse con un cavaliere su una scacchiera in modo tale che ogni quadrato sia atterrato solo una volta e il cavaliere ritorni nello spazio su cui ha iniziato . Alcuni altri problemi di teoria dei grafi sono rimasti irrisolti per secoli .

Il destino di Königsberg

Mentre la teoria dei grafi fiorì dopo che Eulero risolse il problema del ponte di Königsberg, la città di Königsberg ebbe un destino molto diverso. Nel 1875, la gente di Königsberg decise di costruire un nuovo ponte, tra i nodi B e C, aumentando il numero di collegamenti di queste due masse terrestri a quattro. Ciò significava che solo due masse terrestri avevano un numero dispari di collegamenti, il che dava una soluzione piuttosto semplice al problema. La creazione del ponte extra può o non può essere stata inconsciamente causata dal desiderio di un percorso per risolvere il famoso problema della città.

Tuttavia, un nuovo ponte non risolse tutti i problemi futuri di Königsberg, poiché la città non si aspettava nel diciannovesimo secolo, “il triste e lacerato destino che la aspettava come ospite per una delle più feroci battaglie della seconda guerra mondiale.”Durante quattro giorni nell’agosto 1944, i bombardieri britannici distrussero sia la città vecchia che la parte settentrionale di Königsberg. Nel gennaio e febbraio 1945, la regione che circonda Königsberg è circondata dalle forze russe. I civili tedeschi iniziano ad evacuare dalla città, ma si muovono troppo tardi. Migliaia di persone vengono uccise cercando di fuggire in barca ea piedi attraverso le gelide acque della laguna dei Curi. Nell’aprile del 1945, l’Armata Rossa cattura Königsberg con circa il novanta per cento della città vecchia che giace in rovina.

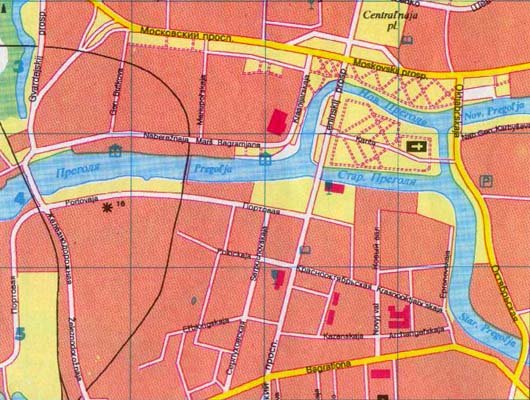
Di seguito è riportata una mappa stradale attuale di Königsberg . Questa mappa mostra quanto la città è cambiata. Molti dei ponti sono stati distrutti durante i bombardamenti, e la città non può più fare la stessa domanda intrigante che erano in grado di nel XVIII secolo. Insieme a un layout molto diverso, la città di Königsberg ha un nuovo nome, Kaliningrad, con il fiume Pregel ribattezzato Pregolya . Mentre il destino di Königsberg è terribile, il vecchio problema del caffè dei cittadini di attraversare ciascuno dei loro vecchi sette ponti esattamente una volta ha portato alla formazione di un ramo completamente nuovo della matematica, la teoria dei grafi.

Biggs, Norman L., E. K. Lloyd, e Robin J. Wilson. Teoria dei grafi: 1736-1936. Oxford: Clarendon Press, 1976.

Dunham, William. Eulero: Il Maestro di tutti noi. Washington: La Mathematical Association of America, 1999.

Eulero, Leonhard, ‘Solutio problematis ad geometriam situs pertinentis’ (1741), Eneström 53, MAA Euler Archive.

“History of Mathematics: On Leonhard Euler (1707-1783).”ScienceWeek (2003). 6 Novembre 2005.e ‘il momento di fare un salto di qualita’. “La verità su Königsberg.”College Mathematics Journal (2004), 35, 198-207.

“Ponti Konigsberg.”The MacTutor History of Mathematics Archive:
http://www-history.mcs.st- and.ac.uk/history/Miscellaneous/other_links/Konigsberg.html

Nota del redattore: Questo articolo è stato originariamente pubblicato in Convergenza, Volume 3 (2006).