Il teorema dei quattro colori
La congettura dei quattro colori è stata dichiarata per la prima volta poco più di 150 anni fa e infine dimostrata in modo conclusivo nel 1976. È un esempio eccezionale di come le vecchie idee si combinano con nuove scoperte e tecniche in diversi campi della matematica per fornire nuovi approcci a un problema. E ‘ anche un esempio di come un problema apparentemente semplice è stato pensato per essere ‘risolto’, ma poi è diventato più complesso, ed è il primo esempio spettacolare in cui un computer è stato coinvolto nella dimostrazione di un teorema matematico.
Inizio
La congettura che qualsiasi mappa, becoloured utilizzando solo quattro colori prima apparizione in una lettera fromAugustus De Morgan (1806-1871), primo professore di matematica al nuovo University College di Londra, per il suo amico William RowanHamilton (1805-1865) il famoso matematico Irlandese nel 1852. Era stato suggerito a De Morgan da uno dei suoi studenti, FrederikGuthrie, a nome del fratello maggiore Francis (che in seguito divenne professore di matematica all’Università di Città del Capo).


Augustus De Morgan (1807-1871) andWilliam Rowan Hamilton (1805-1865)
Il problema, così, semplicemente descritto, ma così allettante difficultto dimostrare, ha catturato l’immaginazione di molti matematici, in time. Alla fine del 1860 De Morgan anche preso il problema e hisproof in America dove tra gli altri, Benjamin Peirce (1809-1880) afamous matematico e astronomo, si interessò in esso come via per sviluppare i suoi metodi logici.
De Morgan ha usato il fatto che in una mappa con quattro regioni, ciascuna delle quali è completamente racchiusa dagli altri. Dal momento che non riusciva a trovare un modo per dimostrarlo, lo usòcome un assioma , la base della sua prova.
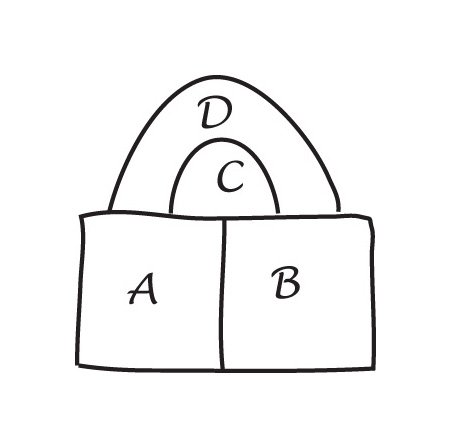
Una copia dell’originale di De Morgan nella sua lettera a Hamilton e una semplice mappa a quattro colori.
Nel 1878 Arthur Cayley (1821-1895) in una riunione della LondonMathematical Society chiese se qualcuno avesse trovato una soluzione per la domanda originale di De Morgan, ma sebbene ci fosse stato qualche interesse, nessuno aveva fatto progressi significativi. Cayley divenne interessato al problema e nel 1879 pubblicò un breve articolo sulla colorazione delle carte in cui spiegava alcune delle difficoltà nel tentare una dimostrazione e apportò alcuni importanti contributi al modo in cui il problema veniva affrontato. La sua domanda: “se una particolare mappa è già colorata con successo con quattro colori, e aggiungiamo un’altra area, possiamo ancora mantenere la stessa colorazione?”ha iniziato un’altra linea di indagine che ha portato all’applicazione dell’istruzione matematica al problema.

Arthur Cayley (1821-1895)
Arthur Cayley ha dimostrato che se fourcolours era già stato utilizzato per colorare una cartina e di una nuova regione wasadded, non sempre è stato possibile per mantenere il originalcolouring.
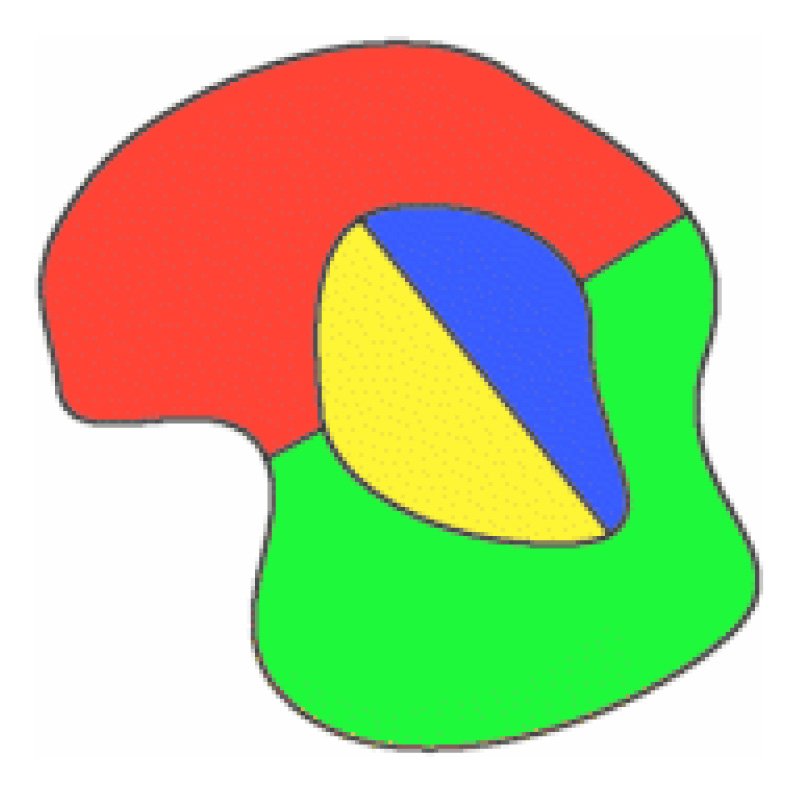
Sopra, tutti e quattro i colori sono stati utilizzati sulla mappa originale, e una nuova regione è disegnata per circondarla. In questo caso, una regione rossa è cambiata in blu, in modo che il rosso possa essere utilizzato sulla nuova regione circostante.
Cayley ha anche osservato che era possibile risolvere una versione del problema limitando il modo in cui i confini si incontravano. Ad esempio, le mappe in cui solo tre paesi si sono incontrati hanno tre bordi che si incontrano ad avertex. Queste sono chiamate “mappe cubiche” e le mappe utilizzate nella discussione seguente sono tutte mappe cubiche. Inoltre, se una mappa può essere colorata con quattro colori, solo tre colori appariranno sul bordo.
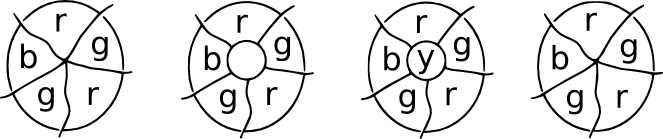
La dimostrazione della patch. Immagina quelloin qualche posto in una mappa un certo numero di paesi si incontrano in un punto. Orametti una patch sul punto d’incontro e tutti i nuovi punti d’incontro avranno tre bordi che emanano da essi. Queste sono mappe cubiche e un quarto colore può essere usato per la regione centrale. Dopo aver rimosso la patch, possiamo tornare alla colorazione originale.
Alcune vecchie tecniche, nuove condizioni e più problemi!
Per seguire gli sviluppi del problema, dobbiamo investigare brevemente alcune delle idee, procedure e tecnicheche i matematici hanno sviluppato nei loro tentativi di risolverlo.
L’unica congettura di cinque vicini
‘Se non riesci a risolvere un problema particolare, trova uno più facile che puoi risolvere.”(Polya. Come risolverlo)
‘Ogni mappa ha almeno un paese con cinque o meno vicini.’
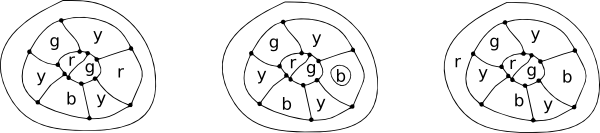
Immagina una mappa di un’isola circondata dal mare. Nella colorazione dei paesi dell’isola, contiamo il mare come una regione. Alcuni paesi possono avere solo due confini (un digon), somethree (come in un triangolo), alcuni quattro (un quadrato) e alcuni cinque (apentagon) o più.
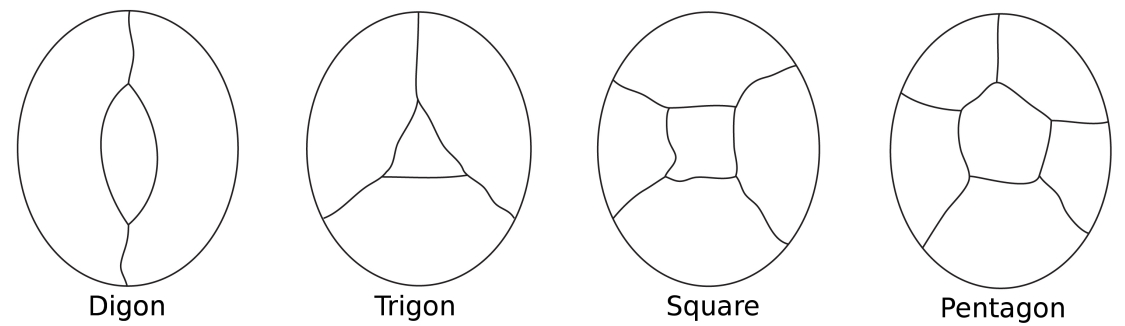
Le più semplici possibiliconfigurazioni per circondare una regione centrale.
Si noti che in tutte queste configurazioni ogni nodo ha solo treedges.
Nel 1813, la formula di Eulero per i poliedri fu adattata per due dimensioni da Augustin Cauchy (1759-1857) proiettando il poliedro su un piano formando così la rete del solido. In questo modo la formula è diventata f f + v-e = 1 becaus, perchéeCauchy non ha contato la regione “esterna” della rete.

Augustin Cauchy (1759-1857)
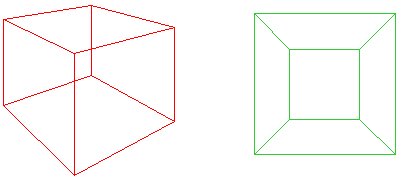
Immaginare che schiacci il cubo rosso downonto di un piano in modo che la sua base è aperto a formare il outsideedge della rete verde. L’idea di Cauchy era di tagliare una faccia delcubo, in modo che per un poligono piano, f f + v – e = 1$. In alternativa, se l ‘”esterno” della rete è considerato come una faccia con infinitearea, allora abbiamo ancora f f + v – e = 2
Possiamo supporre che ci siano almeno tre linee di confine (bordi)che emergono da ciascun punto di incontro (vertici).
La prova che la mappa ha almeno un paese circondato da cinque o meno vicini procede per contraddizione. Se questo porta a un’assurdità, abbiamo una prova.
Ora metti questi valori nella formula di Eulero: f f + v-e = 2 and eabbiamo have 1/3(e) + 2/3(e) – e!che è zero!
Questa è l’assurdità, quindi la nostra ipotesi originale era falsa.Ciò significa che ci deve essere almeno un paese con cinque o meno vicini!
Criminali minimi!
Un altro modo per affrontare il problema dei quattro colori è presumere che sia falso e vedere dove questo porta. Supponiamo che ci siano mappe che hanno bisogno di cinque colori o più, e scegliamo le mappe con il più piccolo numero possibile di paesi. Queste mappe sono chiamate contro-esempi minimi ocriminali minimi !
Quindi questo significa che un criminale minimo non può essere colorato con quattro colori,ma qualsiasi mappa con meno paesi può essere colorata con quattro colori. Se possiamo dimostrare che i criminali minimi non possono esistere, allora potremmo essere in grado di fare qualche progresso.
Ad esempio, possiamo dimostrare che un criminale minimo non può contenere un digon.
Dalla mappa originale, togli un confine dal digon, e otteniamo una nuova mappa con meno paesi. Questa mappa può essere colorata con quattro colori (dal nostro presupposto). Quindi coloriamo questa newmap, (abbiamo solo bisogno di due colori). Ora sostituisci il bordo che abbiamo rimosso e ricolora la mappa. Abbiamo usato tre colori, e dal momento che thereis ancora un altro colore disponibile, questo dimostra che la nostra mappa può becoloured con quattro colori. Ma questo è contro la nostra ipotesi, quindi un criminale minimo non puòcontenere un digon.
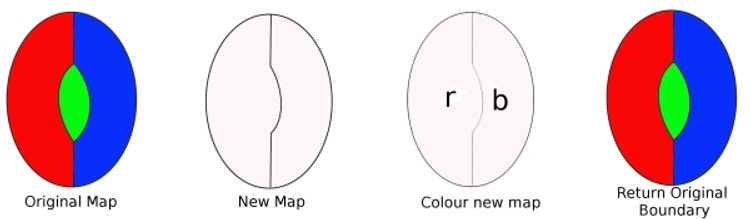
Per mostrare che un Criminalcannot minimo contiene una regione con due bordi (un digon). Supponiamo che ci sia un criminale minimo che contiene un digon. La rimozione di un bordo significa che la mappa contiene meno regioni. Quindi questa nuova mappa può essere coloratacon quattro colori. Ora sostituisci il bordo perso. Poiché prima erano necessari solo due colori, sostituire il bordo significa che possiamo usare un terzo colore e avere ancora un quarto colore da usare. Quindi, un minimalcriminal può essere colorato con quattro colori. Quindi un minimalcriminal non può contenere un digon.
Questa procedura può essere ripetuta per mostrare che un criminale minimonon contiene un paese a tre lati (un trigon), ma si rompe quando proviamo la tecnica su un quadrato, perché quando sostituiamo il quadrato, i paesi accanto ad esso potrebbero usare tutti i quattrocolori, quindi la procedura di prova fallisce. Una volta che questo è accaduto, diventa ovvio che non funzionerà per i pentagoni e così via.
Il teorema dei sei colori
Una tecnica simile può essere applicata per dimostrare che il teorema dei sei colori è vero. Innanzitutto, assumiamo che non ci siano mappe che possano esserecolorato con sei colori. Alcune mappe possono essere colorate con sette colori, quindi selezionando uno di questi (un criminale minimo), se possiamo mostrare che è possibile colorarlo con meno di sette colori, abbiamo raggiunto il nostro obiettivo.
Dalla dimostrazione del teorema dei cinque vicini, è possibile toproceed usando l’idea criminale minima per mostrare che qualsiasi mappa può essere colorata con sei colori!
Dalle regioni ai nodi, alle reti e alla topologia
Nel 1879 Alfred Kempe (1849-1922), utilizzando tecniche simili a quelle descritte sopra, iniziò dalla “proprietà dei cinque vicini” e sviluppò una procedura nota come metodo delle “Catene di Kempe” per trovare una dimostrazione del Teorema dei quattro colori. Ha pubblicato questa prova inl’American Journal of Mathematics. Trovò due versioni più semplici che furono pubblicate l’anno successivo, e la sua prova rimase per dieci anni prima che Percy Heawood (1861-1955) mostrasse che c’era un errore importante nel metodo di prova che Kempe aveva usato.


Alfred Kempe (1849-1922), PeterGuthrie Tait (1831-1901) e Percy Heawood (1861-1955)
Nel 1880 P. G. Tait (1831-1901) un fisico matematico, offereda soluzione al problema. Indipendentemente, Tait aveva stabilito che le mappe in cui un numero pari di linee di confine si incontrano in ogni punto,potevano essere colorate con due colori, sebbene questo risultato fosse apparso in precedenza nei documenti di Kempe.
Durante il 1876-77 Tait divenne noto per il suo studio eclassificazione dei nodi. A quel tempo c’erano un certo numero didiverse teorie sulla struttura degli atomi. William Thompson (Più tardi, Lord Kelvin 1824-1907) ispirato dagli esperimenti del fisico tedesco Hermann von Helmholtz (1821-1894) propose ateoria che gli atomi fossero tubi annodati di etere. La teoria di Kelvin degli “atomi di torsione” è stata presa sul serio per circa vent’anni e ha ispirato Tait a intraprendere una classificazione dei nodi. Tait, Thomson e James Clark Maxwell (1831-1879) inventarono molte idee topologichedurante i loro studi. Tuttavia, la teoria di Kelvin era fondamentalmentemistaken e fisici hanno perso interesse nel lavoro di Tait.


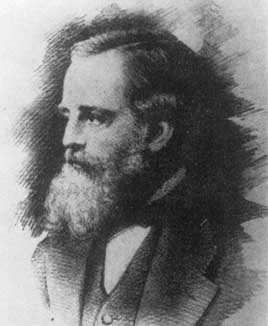
Hermann von Helmholtz (1821-1879),Lord Kelvin (1824-1907) e James Clark Maxwell (1831-1879)

Tait ha iniziato con i modi in cui un solo loop chiuso di cordino può essere annodato. Non aveva un metodo sistematico all’inizio, e cominciò in modo intuitivo prendendo un unico anello chiuso e sperimentando i modi in cui poteva essere annodato. Naturalmente, il cavo doveva essere aperto (come ashoelace) quindi annodato e unito. Si noti che se si segue thecord intorno al nodo, gli incroci ‘over-under’ si alterneranno.Ha poi continuato a sperimentare con due anelli e i modi in cuiessi potrebbero essere annodati insieme. Qui sono mostrati nodi con un massimo di seiattraversamenti per un singolo ciclo.
Uno dei risultati dello studio di Tait fu la sua congettura di grafi hamiltoniani.
Una mappa è considerata come un poliedro disegnato su una sfera, e puòpoi essere proiettata su un piano. Tait ha proposto che qualsiasi mappa cubicpolyhedral abbia un Hamiltoniancycle . Il metodo di Tait si concentrò sui bordi del grafico e mostrò che un ciclo hamiltoniano poteva produrre una mappa di quattro colori. Fu solo nel 1946 che William Tutte (1917-2002) trovò il primo controesempio alla congettura di Tait.
Tait e la connessione con i nodi
Taitiniziò lo studio degli snark nel 1880, quando dimostrò che il teorema di fourcolour era equivalente all’affermazione che nessuno snark isplanar. Un grafico planare è uno che può essere disegnato nel piano connessun incrocio di bordi. Sembra che l’idea di Tait di graphsmight non planare provenga dal suo studio dei nodi e dei percorsi Hamiltoniani .
Il primo snark conosciuto fu il grafico di Petersen scoperto nel 1898,e i matematici iniziarono a cercare più di questi tipi di grafima non fu fino al 1946 che fu trovato un altro snark.
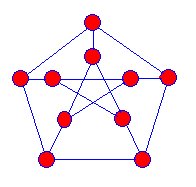 |
Snarks sono proiezioni tridimensionali grafici su theplane. Non ci sono vertici in cui i bordi blu sembrano incrociarsi. Gli snark hanno le seguenti proprietà:
|
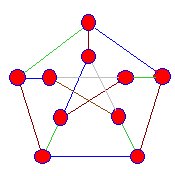 |
I bordi che incontrano i vertici di questo snark sono colorati di blu,verde e marrone, ma raggiungiamo sempre uno stadio in cui questo processonon può essere continuato. |
Giulio Peterson (1839-1910)
La Caccia theSnark è una poesia scritta da Lewis Carroll, e Martin Gardnernamed questi grafici Snarks, perché erano così sfuggente.
Trasformare il problema e trovare nuovi metodi.
Sebbene Heawood trovasse il difetto principale nel metodo di dimostrazione di Kempe nel 1890, non fu in grado di provare il teorema dei quattro colori, ma fece un passo avanti significativo e dimostrò in modo conclusivo che tutte le mappe potevano essere colorate con cinque colori.
Heawood ha dato molti importanti contributi al problema, spostando il focus dell’attenzione dalle aree di una mappa, ai confini tra di loro. Nel 1898 aveva dimostrato che se il numero di bordi attorno a ciascuna regione è divisibile per 3, allora le regioni potevano essere colorate con quattro colori.
La dimostrazione di Cauchy della formula di Eulero includeva anche l’idea chequalsiasi rete di un poliedro può essere triangolata aggiungendo bordi per rendere le facce non triangolari in triangoli. Ha poi sviluppato un procedurewhereby ha cancellato i bordi uno per uno, mostrando che la formula di Eulero potrebbe essere mantenuta ad ogni passo.
La prova di Cauchy della Formula di Eulero
La prova di Cauchy del 1813 della Formula di Eulero iniziò con l’idea di aproiezione di un poliedro per ottenere una rete piana. Egli furtherdemonstrated (a) che qualsiasi rete potrebbe essere triangolato, e la sua prova(b) di Formula di Eulero è stato accettato al momento.
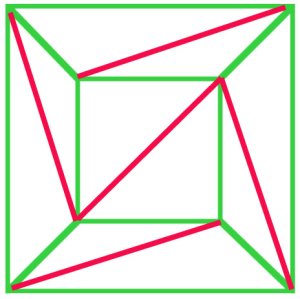 (a)
|
In principle, every polygonal net can be triangulated. In thisnet of a cube (a), $f + v – e$ is $10 + 8 – 17 = 1$, and Euler’sformula still holds. |
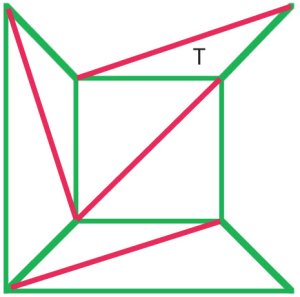 (b)
|
Cauchy discorso per rimuovere i bordi esterni dal diagramma(a) uno per uno, e quando ha raggiunto uno stadio come in figura (b)rimosso l’intero triangolo T, preservando così la formula di Eulero. Molti matematici del primo diciannovesimo secolo concordarono sul fatto che questoprocedura dimostrò una prova della formula di Eulero per tutti i poliedri. |
Nel 1900, i matematici sapevano che un grafico planare poteva esserecostruito da qualsiasi mappa usando il potente concetto di dualità . Nel duale, le regioni sono rappresentate da vertici e due vertici sono uniti da un bordo se le regioni sono adiacenti. In questi grafici, la congettura di FourColour ora chiede se i vertici del grafo possono essere colorati con 4 colori in modo che non ci siano due vertici adiacenti dello stesso colore.
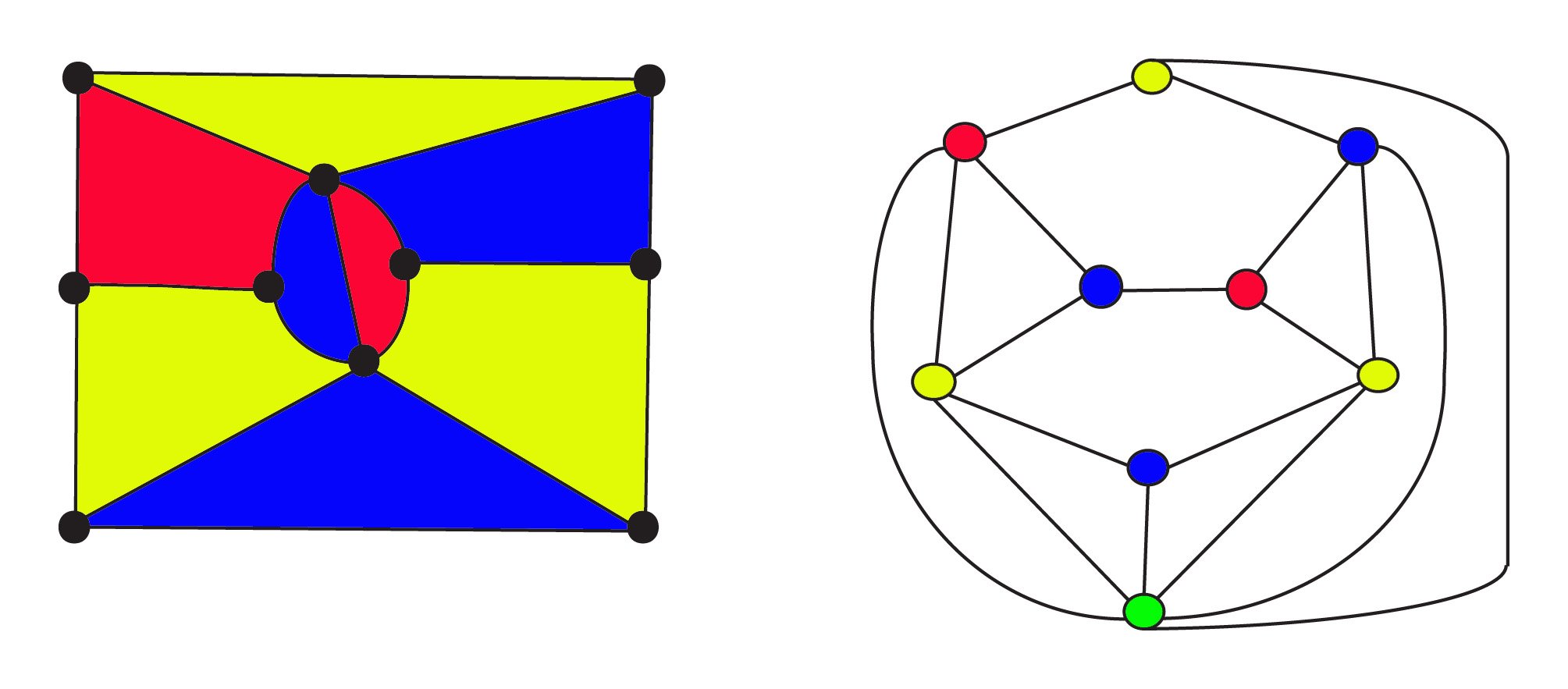
3-color mappa sulla sinistra è di$8$ regioni $10$ vertici e $17$ bordi. La sua doppia grafico sull’theright è di $9$ regioni $9$ vertici e $17$ bordi dove thevertices sono colorate le stesse aree della mappa. Il greenvertex nella parte inferiore del grafico rappresenta l’area esterna infinita per la mappa. Sia la mappa originale che il suo doppio obbediscono alla forma di Eulero per le reti f f + v-e = 1 or o, or \ text {regions} + \ text{vertices}- \ text{edges} = 1$. La relazione di dualità è simmetrica: il duale del duale sarà il grafico originale, dove si scambiano regioni e vertici.
Durante la prima metà del ventesimo secolo, i matematici si concentrarono sulla modifica di questo tipo di tecniche per ridurre le mappe complicate a casi speciali che potevano essere identificati e classificati, per investigare le loro proprietà particolari e sviluppare l’idea di un insieme minimo di configurazioni di mappe che potevano essere testate.
In primo luogo, si pensava che il set contenesse quasi 9.000 membri,il che era un compito enorme, e così i matematici si sono rivolti alle tecniche informatiche per scrivere algoritmi che potevano fare il test per loro. Gli algoritmi hanno utilizzato versioni modificate dell’idea originale di Kempe delle catene insieme ad altre tecniche per ridurre il numero di membri del set minimo.
Dopo aver collaborato con John Koch sul problema della riducibilità, nel 1976 all’Università dell’Illinois, Kenneth Appeland Wolfgang Haken alla fine ridusse il problema dei test a un set inevitabile con 1.936 configurazioni, e fu raggiunta una soluzione completa alla congettura a quattro colori. Questo problema di controllare la riducibilità delle mappe una per una è stato ricontrollato con diversi programmi e diversi computer. La loro prova ha mostrato che almeno una mappa con il minor numero possibile di regioni che richiedono cinque colori non può esistere.
Sin dalla prima dimostrazione, sono stati trovati algoritmi più efficienti per le mappe a 4 colori e, nel 1994, l’inevitabile set di configurazioni era stato ridotto a 633.
Una “prova” eseguita su un computer è una prova corretta?
Poiché la prova è stata fatta con l’aiuto di un computer, c’è stata una protesta immediata. Molti matematici e filosofi hanno affermatoche la prova non era legittima. Alcuni hanno affermato che le prove dovrebbero essere “dimostrate” solo da persone, non da macchine, mentre altri, di una mente più pratica, hanno messo in dubbio l’affidabilità degli algoritmi e la capacità delle macchine di eseguirle senza errori.Tuttavia, molte delle prove scritte dai matematici sonotrovato essere difettoso, quindi l’argomento sull’affidabilità sembra vuoto.Indipendentemente dalle opinioni espresse, la situazione ha prodotto una seria discussione sulla natura della prova che continua ancora oggi.
Per le note pedagogiche:
Utilizzare la scheda note nella parte superiore di questo articolo o fare clic qui .
Note
- Maggiori dettagli di questa e delle altre procedure trovate in questasezione possono essere visti nel libro di Robin Wilson Four Colours Enough .
- I nodi possono essere mancini o destrorsi, e oggi ci sonoimportanti applicazioni di questa proprietà in chimica, farmacia,biologia e fisica. (Vedi Note pedagogiche)
- Prende il nome da William Rowan Hamilton (1805-1865). Un percorso hamiltoniano in un grafico visitaogni vertice esattamente una volta. Un ciclo hamiltoniano (o circuito) è apath che visita ogni vertice esattamente una volta e ritorna al vertice di partenza.(Vedi Note pedagogiche)
- Il libro di Imre Lakatos, Proofs and Confutations ha una discussione e una critica alla procedura di Cauchy (pagine 6 – 12), e molto altro sulla storia del Teorema di Eulero.
- L’idea di dualità sorse nel xvi e xvii secolo consviluppi in geometria proiettiva. Matematici come Pascal andDesargues hanno scoperto che nuovi teoremi potrebbero essere trovati scambiando i termini “punto” e “linea” nelle descrizioni di determinate configurazioni geometriche. Un esempio è in poliedri regolari, dove ilvertici di uno corrispondono alle facce dell’altro. Quindi il duale di un tetraedro è un altro tetraedro, e il duale di un cubo è un ottaedro. Il doppio del doppio è l’originalepoliedro.
Il libro più popolare e facile da leggere sul Four ColourTheorem è:
Wilson, R. (2003)
Bastano quattro colori.
Londra. Penguin Books.
Per una storia più dettagliata e tecnica, il libro standardreference è:
Biggs, N.; Lloyd, E. &Wilson, R. (1986) (1998)
Graph Theory,1736-1936
Oxford. Oxford University Press.
Questo ci porta fino ad oggi, con basi più recenti e filosofia.
Fritsch, R e Fritsch, G (2000)
The Four Color Theorem: History,Topological Foundations, and Idea of Proof
New York. Springer-Verlag.
Quasi nessun libro di storia generale ha molto sull’argomento, ma l’ultimo capitolo di Katz chiamato “Computers and Applications” ha una sezione sulla teoria dei grafi, e il Teorema dei quattro colori è menzionato due volte.
Polya G. Come risolverlo.
Questo è il classico libro sulla risoluzione dei problemi. Ci sono edizioni beenmany di questo libro da quando è apparso per la prima volta nel 1950 andit è ancora facilmente disponibile. Curiosamente, le ultime edizioni hanno dato il sottotitolo ‘Un nuovo aspetto del metodo matematico’.
Lakatos, I. (1976) Prove erifutazioni: La logica della scoperta matematica.
Cambridge. C. U. P.
Questo è un altro libro importante che ha portato alla ricerca intoProblem Solving e indagini nel 1970. Inizia come una discussione in aula tra un insegnante e un gruppo di studenti sulla prova della formula di Eulero, e spazia attraverso le idee,le obiezioni e le possibilità che sono state effettivamente discusse da matematici e scienziati nel diciannovesimo secolo. Solleva alcune delle questioni più importanti sull’insegnamento e la risoluzione dei problemi di apprendimento e sui metodi matematici e le prove.
Riferimenti correlati
Ho avuto un piccolo libro sui giochi di stringhe per qualche tempo. Quando ero a scuola si chiamava Cat’s Cradle, e l’abbiamo suonato nel nostro tempo di rottura.
Recentemente, una rivista francese ha pubblicato un articolo sull’algebra delle figure di stringa! Se vai su Amazon troverai un libro di Ann Swain e Michael Taylor chiamato Finger Strings: A Book of Cats Cradles andString Figures che sarà pubblicato da Floris books nel settembre 2008. Ci sono circa 80 figure descritte con colori diagrams.It la spirale è legata, quindi rimarrà aperta mentre segui le istruzioni. Inoltre è dotato di un paio di anelli di stringa!
Per gli esperti di nodi, L’AshleyBook of Knots è un classico per chiunque sia interessato a centinaia di diversi tipi di nodi e ai loro usi. Amazon hasvarie edizioni disponibili a prezzi diversi.
Collegamenti Web
Per una panoramica generale e collegamenti a molte persone e argomenti, il sito web di Actutor è
E, naturalmente, le biografie di MacTutor di coloro che sono coinvolti nello sviluppo di tutti i diversi aspetti matematici possono essere trovate nell’Indice delle biografie di MacTutor.
Il teorema dei quattro colori e tre prove. Per il mathematicallypersistent il seguente sito web ha un nuovo approccio intrigante toattacking il problema di costruire un nuovo algoritmo per solvingthe problema, e legando per ridurre la dipendenza da un computer.http://www.emu.edu.tr/~cahit/the%20four%20color%20theorem%20—%20three%20proofs.htm
Per la teoria dei grafi, Wikipedia offre una buona panoramica e puoi eseguire le cose veramente tecniche. Mostra i tipi di modernoapplicazioni di quest’area della matematica. Se vai su GraphColouring e fai clic sul Teorema dei quattro colori, troverai molte più informazioni.
Una storia interessante e non troppo tecnica della teoria dei nodi-come un’idea della fisica di Kelvin ritorna alla teoria Atomicaoggi.
L’Associazione degli insegnanti di Matematica hanno Celtic Knotdesign poster. Vai al loro sito web e sfoglia l’alfabeticoelenco delle risorse.
Scopri tutto sui Nodi sull’Atlante dei nodi! Se non sei un esperto-goditi la varietà e la complessità del database “inthe spirit of wiki”
Più artistico e colorato – ma non meno matematico è il sito di trama diknot.
Per coloro che vogliono alcune delle cose originali e historicaldetail vai alla Storia della Teoria dei nodi su: